Scientific Method Measurements Scientific Method observations Revision different

Scientific Method Measurements

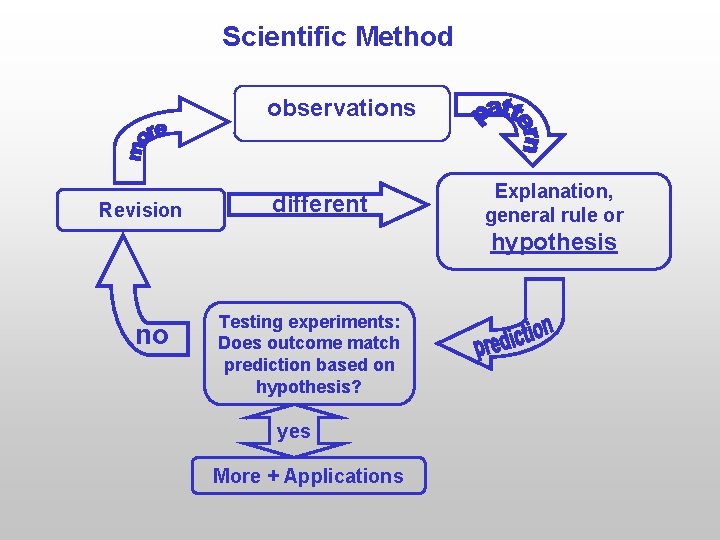
Scientific Method observations Revision different Explanation, general rule or hypothesis no Testing experiments: Does outcome match prediction based on hypothesis? yes More + Applications

Hypothesis An object’s motion always occur in the direction of the force exerted on it by other objects Testing experiment 1. 2. 3. Think and discuss in your group a possible experiments that will test the hypothesis Try to devise supporting and DISPROVING experiments. Draw a LABELED picture/sketch of the experiments showing directions of the force and the motion

Measurements 1. 489 m A. They have the same lengths B. They have different lengths C. I do not know. 1. 485 m

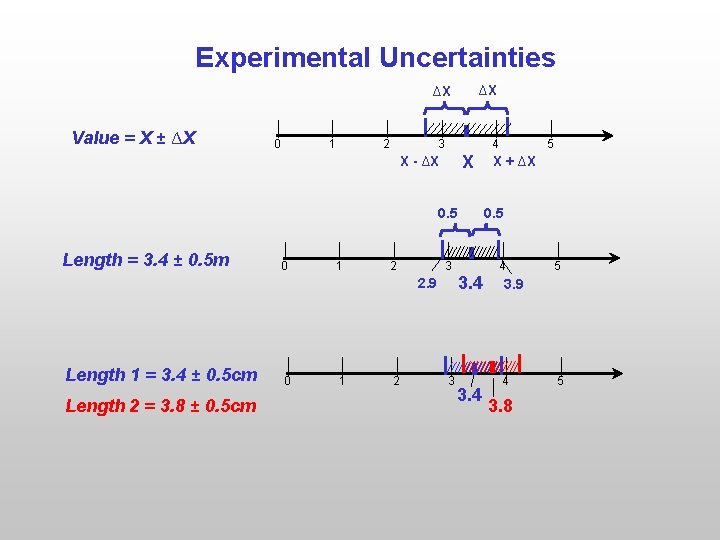
Experimental Uncertainties ∆X ∆X Value = X ± ∆X 0 1 2 3 4 X X - ∆X 0 1 2 3 Length 1 = 3. 4 ± 0. 5 cm Length 2 = 3. 8 ± 0. 5 cm 0 1 2 4 3. 4 2. 9 3 X + ∆X 0. 5 Length = 3. 4 ± 0. 5 m 5 3. 4 5 3. 9 4 3. 8 5

Sources of Uncertainties Instrumental uncertainties Usually can be estimated as a half of the smallest increment of the instrument scale 0. 5 mm = 0. 05 cm Random Uncertainties

Experimental Uncertainties of measurements 1. Instrumental uncertainties 2. Random Uncertainties Comparison uncertainties Reducing uncertainties Uncertainty in the final calculated value

Controlling Variables At the right are drawings of three strings hanging from a bar. The three strings have metal weights attached to their ends. String 1 and String 3 are the same length. String 2 is shorter. A 10 unit weight is attached to the end of String 1. A 10 unit weight is also attached to the end of String 2. A 5 unit weight is attached to the end of String 3. The strings (and attached weights) can be swung back and forth and the time it takes to make a swing can be timed. Suppose you want to find out whether the length of the string has an effect on the time it takes to swing back and forth. Which strings would you use to find out? a. only one string b. all three strings c. 2 and 3 d. 1 and 3 e. 1 and 2 because a. you must use the longest strings. b. you must compare strings with both light and heavy weights. c. only the lengths differ. d. to make all possible comparisons. e. the weights differ.

Homework (due Monday) Uncertainties Read the text Answer the questions after the text