Scientific Measurements and Conversions August 8 Take out

Scientific Measurements and Conversions August 8 Take out your notebook, label appropriately, copy and solve: Warm-up: How many minutes are in 6. 2 hours? How many dollars does 35 quarters equal?

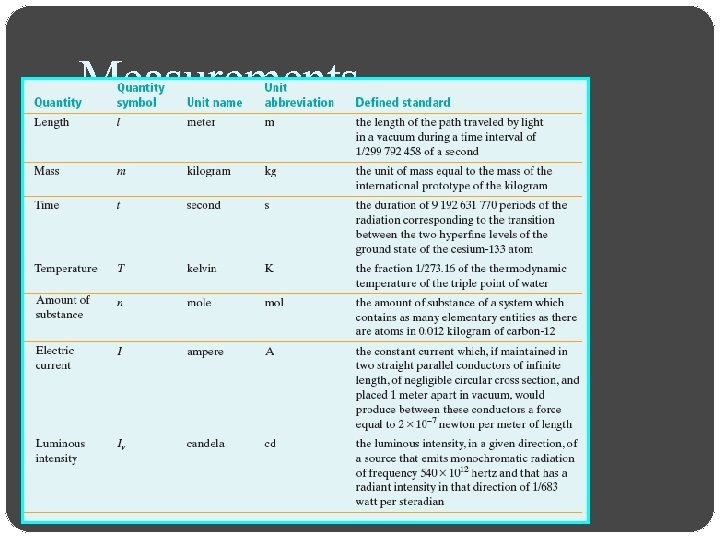
Introduction to Chemistry SCSh 4. Students will use tools and instruments for observing, measuring, and manipulating scientific equipment and materials. a. Develop and use systematic procedures for recording and organizing information. b. Use technology to produce tables and graphs. c. Use technology to develop, test, and revise experimental or mathematical models.

Measurements

With the person next to you, identify one object in the room that has a measurement quantity. Be prepared to discuss the: • unit of measurement • description of the measurement • What other qualities does the object have?

Measurements Review

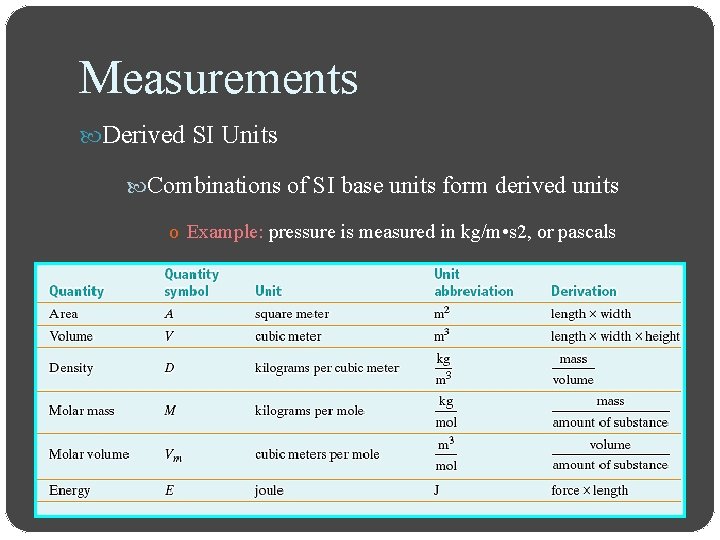
Measurements Derived SI Units Combinations of SI base units form derived units o Example: pressure is measured in kg/m • s 2, or pascals

Measurements Derived SI Units Volume is the amount of space occupied by an object o The derived SI unit is cubic meters, m 3 o The cubic centimeter, cm 3, is often used o 1 m. L = 1 cm 3

Measurements Derived SI Units Density is the ratio of mass to volume, or mass divided by volume o The derived SI unit is kilograms per cubic meter, kg/m 3 o g/cm 3 or g/m. L are also used o Density is a characteristic physical property of a substance

Measurements Derived SI Units Sample Problem o A sample of aluminum metal has a mass of 8. 4 g. The volume of the sample is 3. 1 cm 3. Calculate the density of aluminum

Measurements Derived SI Units Sample Problem Answer o Given: mass (m) = 8. 4 g volume (V) = 3. 1 cm 3 o Unknown: density (D) o Solution:

Measurements Dimensional analysis is a mathematical technique that allows you to use units to solve problems involving measurements Quantity sought = quantity given × conversion factor Example: the number of quarters in 12 dollars number of quarters = 12 dollars × conversion factor

Measurements Conversion Factors Sample Problem o Express a mass of 5. 712 grams in milligrams and in kilograms

Measurements Conversion Factors Sample Problem Answer o Given: 5. 712 g o Unknown: mass in mg and kg o Solution: mg 1 g = 1000 mg Possible conversion factors:

Measurements Conversion Factors Sample Problem Answer o Given: 5. 712 g o Unknown: mass in mg and kg o Solution: kg 1 000 g = 1 kg Possible conversion factors:

Mustang Challenge SEHS is recruiting a live mascot, but wants the biggest and strongest. Complete calculation on notes page from yesterday. Mustang #1: 307. 82 mg #2 : 00. 0756 kg #3 : 48. 004 x 10 -2 g Which mustang weighs the most?

Scientific Measurements

Measurements Accuracy and Precision Accuracy refers to the closeness of measurements to the correct or accepted value of the quantity measured Precision refers to the closeness of a set of measurements of the same quantity made in the same way

Scientific Measurements August 8 Take out your homework sheet and notes from yesterday. Copy and Solve: A flower grows 2. 05 cm for each 50 m. L of water given. How tall will the plant grow is given 10, 000 m. L of water?

Scientific Measurements August 8 Take out your notebook, label appropriately, copy and solve: Warm-up: How many m. L are in one Liter? A flower requires 25 m. L to grow 8 inches. If you feed the flower 158 m. L, how tall will the flower grow?

Scientific Measurements August 9 Take out your notebook, label appropriately, copy and solve: Warm-up: How many hectoliters are in one kiloliter? A flower grows 2. 05 cm for each 50 m. L of water given. How tall will the plant grow is given 10, 000 m. L of water?

DENSITY LAB- Rm. 304 You will need: 1. One sheet of paper 2. Pencil 3. Calculator Observe all lab safety rules - Read and follow all directions - Goggles

Scientific Measurements August 10 Pass your lab to the center, make sure your name is on it Take out your notebook, label appropriately, copy and solve: Warm-up: How many milliliters of water will it take to fill a 2 L bottle that already contains 1. 87 L of water?

Measurements Accuracy and Precision

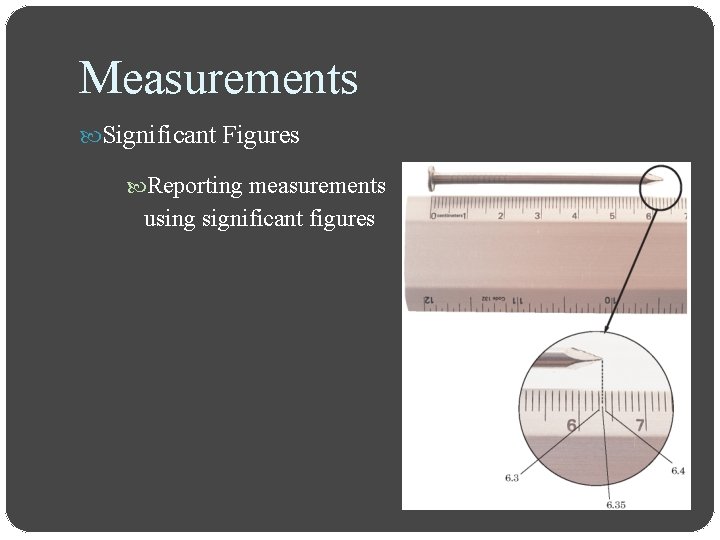
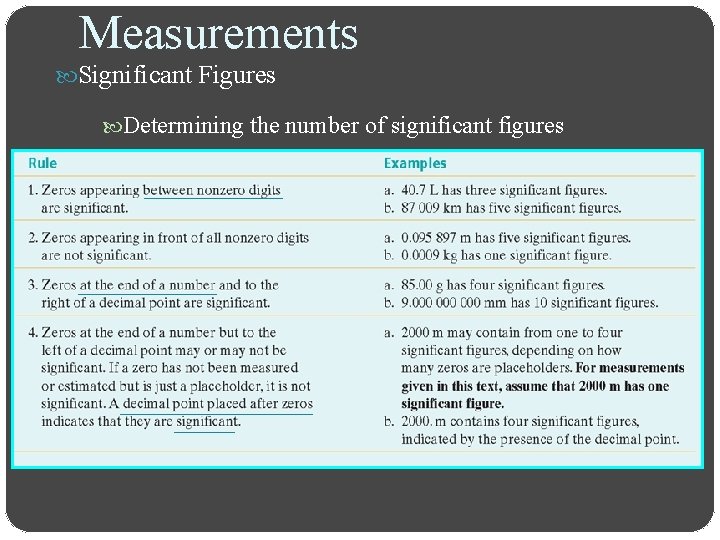
Measurements Significant Figures Significant figures in a measurement consist of all the digits known with certainty plus one final digit, which is somewhat uncertain or is estimated The term significant does not mean certain

Measurements Significant Figures Reporting measurements using significant figures

Measurements Significant Figures Determining the number of significant figures

Measurements Significant Figures Sample Problem o How many significant figures are in each of the following measurements? a. 28. 6 g b. 3440. cm c. 910 m d. 0. 04604 L e. 0. 0067000 kg

Measurements Significant Figures Sample Problem Solution a. 28. 6 g There are no zeros, so all three digits are significant b. 3440. cm By rule 4, the zero is significant because it is immediately followed by a decimal point; there are 4 significant figures c. 910 m By rule 4, the zero is not significant; there are 2 significant figures

Measurements Significant Figures Sample Problem Solution d. 0. 04604 L By rule 2, the first two zeros are not significant; by rule 1, the third zero is significant; there are 4 significant figures e. 0. 006 700 0 kg By rule 2, the first three zeros are not significant; by rule 3, the last three zeros are significant; there are 5 significant figures

Measurements Significant Figures Addition or subtraction with significant figures o When adding or subtracting decimals, the answer must have the same number of digits to the right of the decimal point as there are in the measurement having the fewest digits to the right of the decimal point

Measurements Significant Figures Multiplication or division with significant figures o For multiplication or division, the answer can have no more significant figures than are in the measurement with the fewest number of significant figures

Measurements Significant Figures Sample Problems o Express each answer to the correct number of significant figures a. 5. 44 m - 2. 6103 m b. 2. 4 g/m. L 15. 82 m. L

Measurements Significant Figures Sample Problem Solutions a. 5. 44 m - 2. 6103 m = 2. 84 m There should be two digits to the right of the decimal point, to match 5. 44 m b. 2. 4 g/m. L 15. 82 m. L = 38 g There should be two significant figures in the answer, to match 2. 4 g/m. L

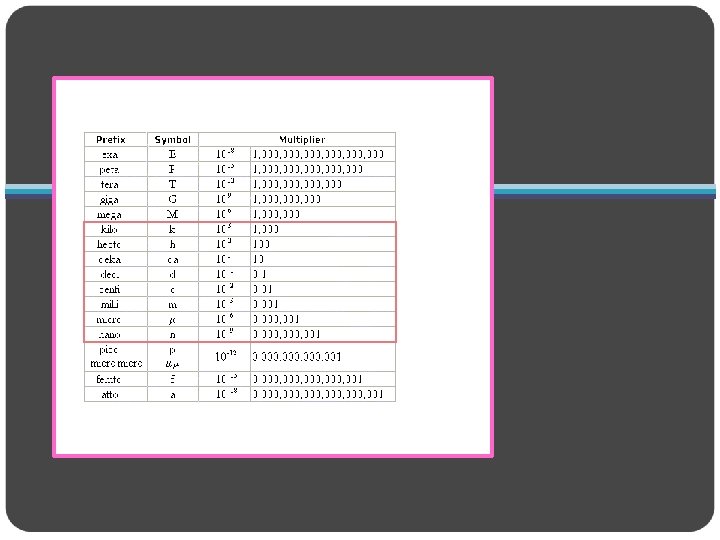
Measurements Scientific Notation In scientific notation, numbers are written in the form M × 10 n, where the factor M is a number greater than or equal to 1 but less than 10 and n is a whole number o Example: 0. 000 12 mm = 1. 2 × 10− 4 mm o Move the decimal point four places to the right and multiply the number by 10− 4

Measurements Scientific Notation Determine M by moving the decimal point in the original number to the left or the right so that only one nonzero digit remains to the left of the decimal point Determine n by counting the number of places that you moved the decimal point. If you moved it to the left, n is positive. If you moved it to the right, n is negative

Measurements Scientific Notation Addition and subtraction —These operations can be performed only if the values have the same exponent (n factor) o Example: 4. 2 × 104 kg + 7. 9 × 103 kg or

Measurements Scientific Notation Multiplication —The M factors are multiplied, and the exponents are added algebraically o Example: (5. 23 × 106 µm)(7. 1 × 10− 2 µm) = (5. 23 × 7. 1)(106 +10 -2) = 37. 133 × 104 µm 2 = 3. 7 105 µm 2

Measurements Scientific Notation Division — The M factors are divided, and the exponent of the denominator is subtracted from that of the numerator o Example: = (5. 44 / 8. 1)(107 -104) = 0. 6716049383 × 103 = 6. 7 102 g/mol

Express the following quantities in scientific notation: a. 8 800 000 m b. 0. 0015 kg c. 0. 000 000 06 kg/m 3 d. 8 002 000 Hz e. 0. 009 003 amp f. 70 000 000 000 km g. 6028 L h. 0. 2105 g i. 600 005 000 k. J/h j. 33. 8 m 2

Matter/ Mixtures August 13 Take out your notebook, label appropriately, copy #2 and solve: Warm-up: 1. A metallurgist is going to make an experimental alloy that requires adding 325 g of bismuth to 2. 500 kg of molten lead. What is the total mass of the mixture in kilograms? 3 2 2. 2. 58 x 10 cm x 3. 3 x 10 cm =

Matter

Matter and Its Properties Matter Volume is the amount of three dimensional space an object occupies Mass is a measure of the amount of matter Matter is anything that has mass and takes up space

Matter and Its Properties of Matter Extensive properties depend on the amount of matter that is present o Volume o Mass o The amount of energy in a substance

Matter and Its Properties of Matter Intensive properties do not depend on the amount of matter present o o o Melting point Boiling point Density Ability to conduct electricity Ability to transfer energy as heat

Matter and Its Properties Physical Properties/Physical Changes Physical property is a characteristic that can be observed or measured without changing the identity of the substance o Color, volume, hardness, temperature o Melting point and boiling point Physical change is a change in a substance that does not involve a change in the identity of the substance o Grinding, cutting, melting, and boiling

Matter and Its Properties Physical Properties/Physical Changes Change of state is a physical change of a substance from one state to another o Solid state, matter has definite volume and definite shape o Liquid state, matter has a definite volume but an indefinite shape o Gas state, matter has neither definite volume nor definite shape o Plasma is a high-temperature physical state of matter in which atoms lose most of their electrons, particles that make up atoms

Physical and Chemical Properties Examples of Physical Properties Boiling point Color Slipperiness Electrical conductivity Melting point Taste Odor Dissolves in water Shininess (luster) Softness Ductility Viscosity (resistance to flow) Volatility Hardness Malleability Density (mass / volume ratio) Examples of Chemical Properties Burns in air Reacts with certain acids Decomposes when heated Explodes Reacts with certain metals Reacts with certain nonmetals Tarnishes Reacts with water Is toxic Ralph A. Burns, Fundamentals of Chemistry 1999, page 23 Chemical properties can ONLY be observed during a chemical reaction!

Physical & Chemical Changes CO 2 crushing heating Pyrex PHYSICAL CHANGE Limestone, Ca. CO 3 CHEMICAL CHANGE Ca. O Crushed limestone, Ca. CO 3 Lime and carbon dioxide, Ca. O + CO 2

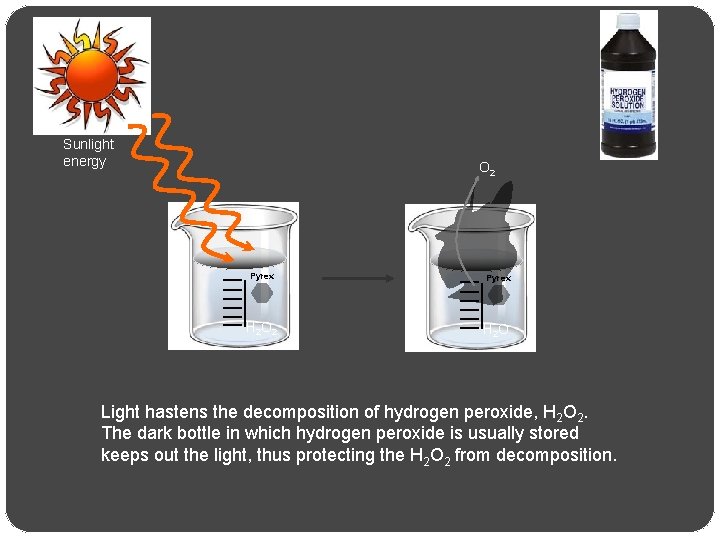
Sunlight energy O 2 Pyrex H 2 O Light hastens the decomposition of hydrogen peroxide, H 2 O 2. The dark bottle in which hydrogen peroxide is usually stored keeps out the light, thus protecting the H 2 O 2 from decomposition.

Matter and Its Properties Physical Properties/Physical Changes

Matter and Its Properties Physical Properties/Physical Changes

Matter and Its Properties Physical Properties/Physical Changes

Matter and Its Properties Chemical Properties/Chemical Changes Chemical property relates to a substance’s ability to undergo changes that transform it into different substances Flammability, toxicity, heat of combustion Chemical change or chemical reaction is a change in which one or more substances are converted into different substances

Matter and Its Properties Chemical Properties/Chemical Changes Iron + Oxygen/Water/Acids = Iron Oxide Magnesium + Oxygen = Magnesium Oxide

Matter and Its Properties Chemical Properties/Chemical Changes Reactants are the substances that react in a chemical change Products are the substances that are formed by the chemical change carbon + oxygen reactants yields carbon dioxide product

Matter and Its Properties Evidence of Chemical Change

Matter/Mixtures August 14 Copy and Solve 1. An airplane descends at 35 mi/hr for 80 minutes. How far did the airplane descend? 2. How many significant figures does 0. 0072070 have? 3. Write the number above in scientific notation.

Calculation Quiz Tomorrow 1. 30 m. L = _______ L 2. Density of an iron ore sample with a mass of 5 kg and a volume of 2. 5 cm(3) 3. 37. 75 m + 3. 876 m= 4. 10 power 3 x 10 power 5 = 5. A swimmer can swim at a consistent rate of 5 m per sec. How may centimeters can the swimmer travel in 1 min? 6. 1. 567 x 10(power 6) ÷. 54 x 10 (power 2)

Matter and Its Properties Energy and Changes in Matter Energy is always involved when physical or chemical changes occur Energy can be in various forms o Heat o Light Energy can be absorbed or released in a change, it is not destroyed or created o Law of conservation of energy

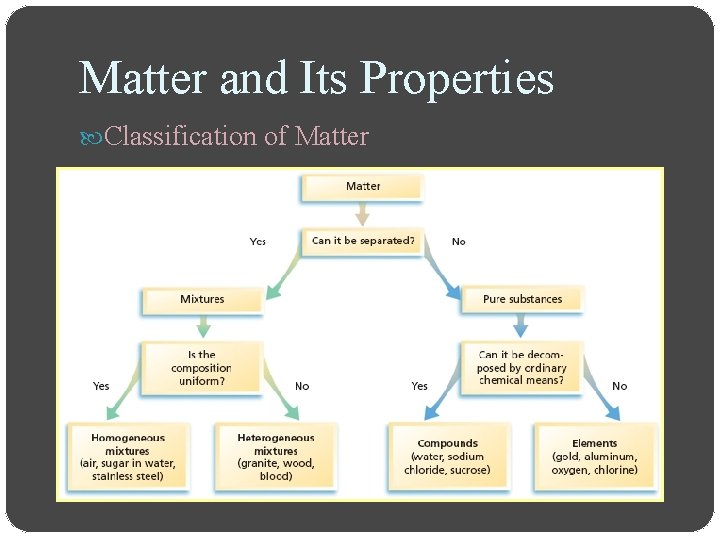
Matter and Its Properties Classification of Matter

Matter and Its Properties Classification of Matter Mixture is a blend of two or more kinds of matter, each of which retains its own identity and properties o mixed together physically o can usually be separated Homogeneous mixtures are called solutions o Uniform in composition (salt-water solution) Heterogeneous mixtures o Not uniform throughout (clay-water mixture)

Matter and Its Properties Give examples of each type of mixture: Homogenous: Heterogeneous:

Matter and Its Properties Give examples of each type of mixture:

Matter and Its Properties Classification of Matter Pure substance has a fixed composition Pure substances are either compounds or elements A pure substance differs from a mixture in the following ways o Every sample of a given pure substance has exactly the same characteristic properties and composition o Example: Water is always 11. 2% hydrogen and 88. 8% oxygen by mass

Matter and Its Properties

MIXTURE LAB The mixture you will work with contains salt, sand, iron filings, and saw dust. All four substances are in dry, granular form. You are to make a plan for what you will do to separate the mixture into the pure substances. You must write out a plan with your partners as to how you will separate the mixture. POSSIBLE MATERIALS aluminum foil cotton balls distilled water forceps magnet paper clips paper towels Petri dish pipets plastic forks plastic spoons plastic straws sample of mixture and components (sand, iron filings, salt, poppy seeds) tissue paper transparent tape wooden splints

Periodic Table August 15 Copy and Solve 3 1. 7. 736 x 10 km / 2 2. 3 x 10 km 2. How many significant figures does 0. 0072070 have? 3. Write the number about in scientific notation.

Calculations QUIZ Show all work to receive full credit. Questions 1, 2, and 5 do not require work to be shown. When you finish, turn your quiz into the 1 st period shelf. Finish completing and reviewing the Chapter 1 and 2 vocabulary.