Scientific Measurement Measurements and Their Uncertainty Measurement quantity

Scientific Measurement

Measurements and Their Uncertainty • Measurement – quantity that has both a number and unit - Example: your height, the temperature outside etc.

Measurements • Measurements are fundamental to experimental sciences - important to decide if measurement is correct

Scientific Notation • Scientific Notation – given number is written as product of two numbers - a coefficient and ten raised to a power Example: 3, 100, 000 = 3. 1 X 106 0. 00000011 = 1. 1 X 10 -7

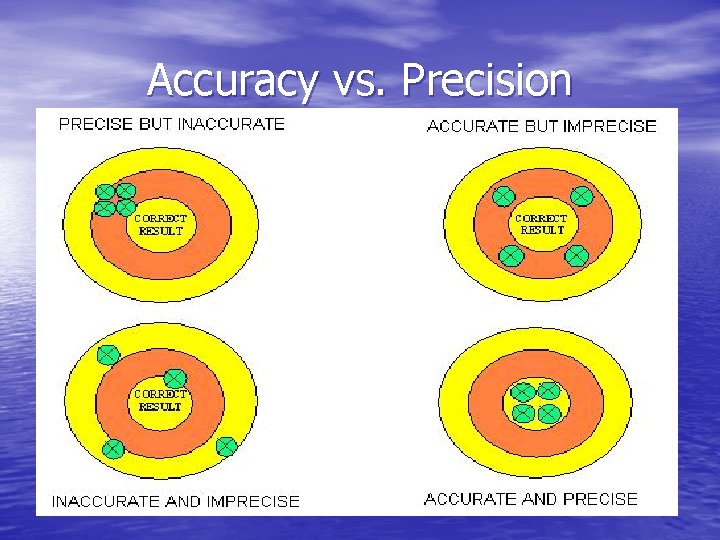
Accuracy vs. Precision • Accuracy – measure of how close a measurement comes to actual or true value - measured value must be compared to correct value • Precision – measure of how close series of measurements are to each other - Consistent - must compare values of two or more repeated measurements

Accuracy vs. Precision

Determining Error • Accepted value – the correct value based on reliable references • Experimental Value – value measured in lab • Error – difference between experimental value and accepted value

Determining Error • Error = experimental value – accepted value • Error can be positive or negative • Example: - water in lab boils at 99. 1˚C - water boils at accepted value of 100. 0˚C • Error = 99. 1˚C – 100. 0˚C = - 0. 9°C

Percent Error • Percent Error – absolute value of error divided by accepted value, multiplied by 100% • Percent – comes from Latin words per, meaning “by” or “through” and centum, meaning “ 100”

Percent Error Percent error = (|error| / accepted) X 100% • Example: Percent error = (|99. 1˚C – 100. 0˚C| / 100. 0˚C) X 100% = (0. 9˚C/100. 0˚C) X 100% = 0. 009 X 100% = 0. 9%

Significant Figures • Significant Figures – all digits that are known, plus a last digit that is estimated • Measurements must be reported to correct number of significant figures - calculated answers depend on number of significant figures

Rules For Significant Digits • Every nonzero digit in reported measurement is assumed to be significant 24. 7 m and 0. 743 m = 3 sig. figs. • Zeros between nonzero digits are significant 7003 m = 4 significant figures • Leftmost zeros in front of nonzero digits are not significant only placeholders 0. 000099 m = 2 significant figures = 9. 9 X 10 -5 m

Rules for Significant Digits • Zeros at end of a number and to the right of a decimal point are always significant 1. 010 m and 9. 000 m = 4 sig. figs. • Zeros at rightmost end of measurement lying to left of understood decimal point are not significant – only placeholders 300 m and 7000 m = 1 sig. fig.

Rules for Significant Digits • Two situations with unlimited number of 1. 2. significant figures: Counting if you count 23 people, there are 23 people Defined quantity 100 cm = 1 m

Significant Figures in Calculations • A calculated answer cannot be more precise than least precise measurement from which it was calculated

Rounding • First decide on number of significant figures • If number to the right of last know significant figure is less than five, drop the digit and keep it the same Example: 2. 33 = 2. 3 at 2 sig. figs. • If number to the right of last know significant figure is 5 or greater increase by 1 Example: 2. 36 = 2. 4 at 2 sig. figs.

Addition and Subtraction • Answer to addition and subtraction calculation should be rounded to same number of decimal places as measurement with least number of decimal places • Example: 12. 52 m + 349. 0 m + 8. 24 m = 369. 8 m = 3. 698 X 102 m

Multiplication and Division • Round answer to same number of significant figures as measurement with least amount of significant figures • Example: 7. 55 m X 0. 34 m = 2. 567 m 2 = 2. 6 m 2

International System of Units • SI – International System of Units - revised version of metric system - Five common base units include: - meter - kilogram - kelvin - second - mole

SI Base Units Quantity SI base unit Length meter Mass kilogram Temperature kelvin Time second Amount of mole Substance Luminous candela intensity Electric ampere Current Symbol m kg K s mol cd A

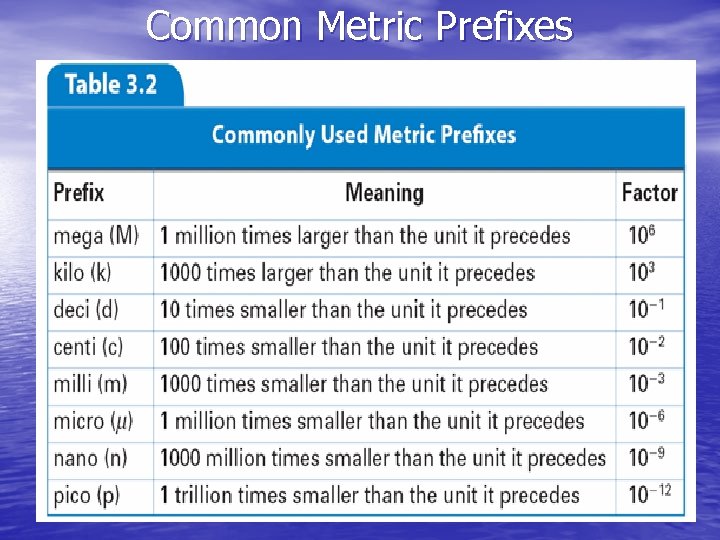
Common Metric Prefixes

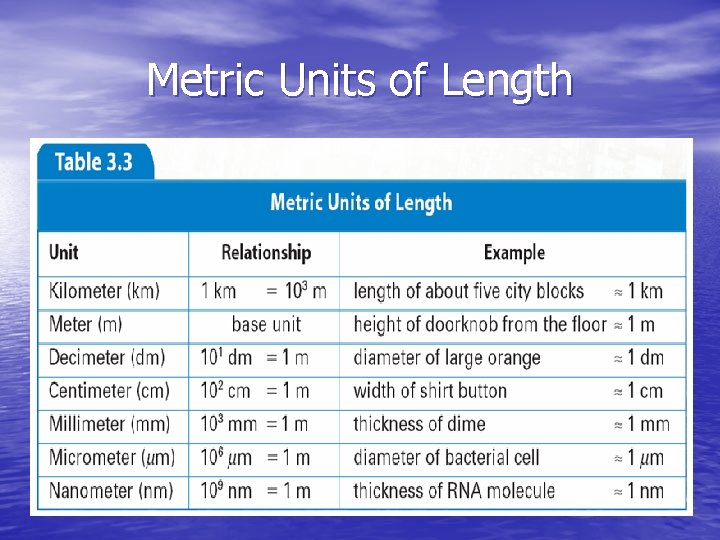
Units of Length • SI unit is meter (m) • Common metric units include: - centimeter - kilometer

Metric Units of Length

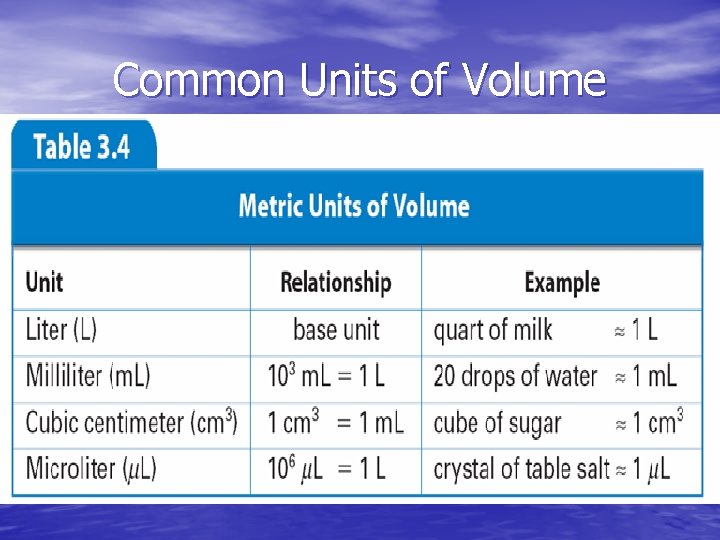
Units of Volume • SI unit is m 3 • Non-SI unit is liter (L) • Common metric units of volume include: - liter (L) - milliliter (m. L) - cubic centimeter (cm 3) - microliter (µL)

Common Units of Volume

Units of Mass • Basic SI unit is kilogram (kg) • 1 gram (g) is 1/1000 of a kilogram • Common metric units of mass include: - kilogram (kg) - gram (g) - milligram (mg) - microgram (µg)

Units of Mass

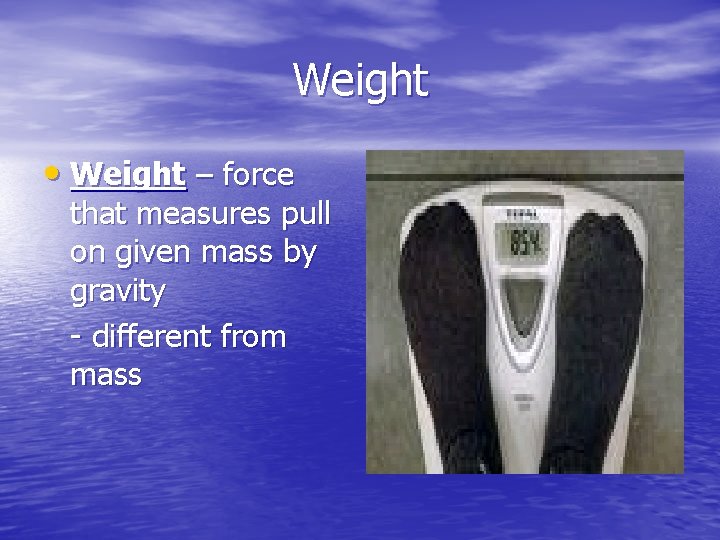
Weight • Weight – force that measures pull on given mass by gravity - different from mass

Units of Temperature • Temperature – measure of how hot or cold and object is - two common equivalent units: - Celsius - kelvin – SI unit

Kelvin scale vs. Celsius scale • Celsius scale – places freezing point of water at 0˚C - boiling point of water at 100°C • Kelvin scale – places freezing point of water at 273. 15 K - boiling point of water at 373. 15 K • Absolute zero = O kelvin (K) - coldest possible temperature known

Kelvin vs. Celsius • Example: 10°C = 283 K 293 K = 20°C

Units of Energy • Energy – capacity to do work or produce heat - common units include joule and calorie - SI unit is joule (J)

Conversion Factors • Conversion Factor – ratio of equivalent measurements - multiplying by conversion factor changes numerical value - actual quantity size remains the same Example: 1000 g/1 kg and 1 kg/1000 g 109 nm/1 m and 1 m/109 nm

Dimensional Analysis • Dimensional Analysis – way to analyze and solve problems using units or dimensions of measurements - alternative approach to problem solving - page 82 -83

Dimensional Analysis • Example: How many minutes are there in one week? 1 week X 7 days X 24 hours X 60 minutes 1 week 1 day 1 hour = 10, 080 minutes or 1. 0080 X 104 minutes • Complete practice problem number 29 page 82

Dimensional Analysis • Example: - mass of copper available = 50. 0 g Cu - each student gets 1. 84 g Cu - How many students are there? 50 g Cu X 1 student = 27. 174 = 27 students 1. 84 g Cu • Complete practice problems 30 and 31 (83)

Converting Between Units • Converting one unit to an equivalent measurement with another unit • Example: mass = 750 dg 1 g = 10 dg Solve for the mass in grams. 750 dg X 1 g = 75 g 10 dg • Complete practice problem 32 and 33 page 84

Multistep Problems Example: length = 0. 073 cm = 7. 3 X 10 -2 cm - convert to µm 102 cm = 1 m 1 m = 106µm 7. 3 X 10 -2 cm X 106µm = 7. 3 X 102µm 102 cm 1 m • Complete 34 and 35 page 85

Converting Complex Units Example: density of manganese = 7. 21 g/cm 3 103 g = 1 kg 106 cm 3 = 1 m 3 ? = kg/m 3 7. 21 g X 1 kg X 106 cm 3 = 7. 21 X 103 kg/m 3 1 cm 3 103 g 1 m 3 • Complete 36 and 37 page 86

Density • Density – ratio of mass to volume of an object • Density = mass/volume

Density • Density is an intensive property depending on composition of substance - does not depend on size of sample

Density • Density of substance generally decrease as temp increases • Calculating Density: mass = 3. 1 g volume = 0. 35 cm 3 Density = 3. 1 g/0. 35 cm 3 = 8. 8571 g/cm 3 = 8. 9 g/cm 3 (rounded to two significant figures) • Complete number 46 and 47 (page 91)

Using Density to Calculate Volume Example: mass of coin = 14 g density of silver = 10. 5 g/cm 3 volume of coin = ? Volume = mass/density 14 g Ag X 1 cm 3 Ag = 1. 3 cm 3 Ag 10. 5 g Ag • Complete 48 and 49 – page 92

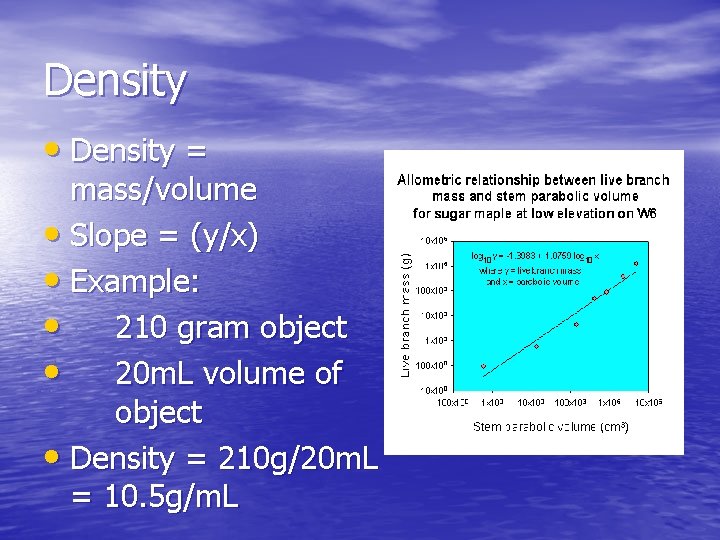
Density • Density = mass/volume • Slope = (y/x) • Example: • 210 gram object • 20 m. L volume of object • Density = 210 g/20 m. L = 10. 5 g/m. L