Scientific Measurement Chapter 3 3 1 Measurements and

Scientific Measurement Chapter 3

3 -1 Measurements and Their Uncertainty Learning Target: To learn to strive for accuracy and precision in measurement. Success Criteria: I can… 1. convert measurements to scientific notation. 2. distinguish among accuracy, precision, and error of a measurement. 3. determine the number of significant figures in a measurement and in a calculated answer.

3 -1 Measurements and Their Uncertainty Using and Expressing Measurements: • Based on what you already know, define measurement. – Measurement is a quantity that has both a number and a unit. – We all use and make measurements… Can you give some examples? • Examples: Temperature, cooking/baking, grades, etc.

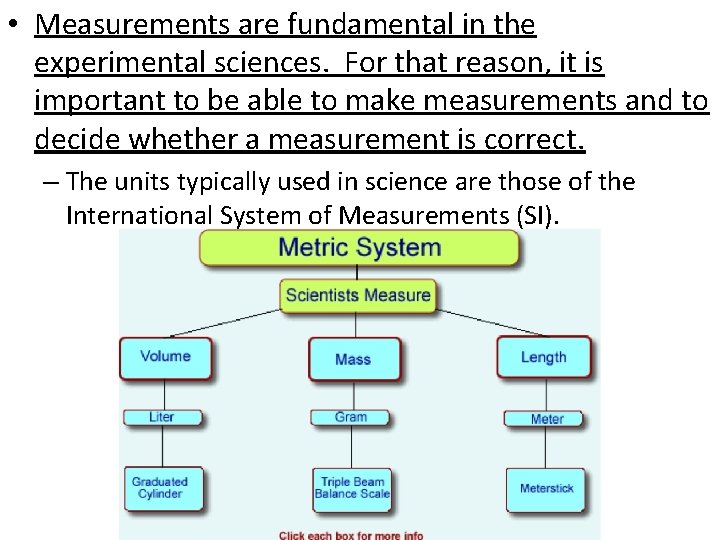
• Measurements are fundamental in the experimental sciences. For that reason, it is important to be able to make measurements and to decide whether a measurement is correct. – The units typically used in science are those of the International System of Measurements (SI).

• Scientific Notation: • This allows us to write really big and really small numbers in a convenient way. – Why wouldn’t we want to find an easier way to write 540, 000, 000? – How to do it: Formula: M x 10 n Where 1 ≤ M < 10 and n = whole number that tells us how many times the decimal moved. Rule: If the original number is greater than 1, n is positive. If smaller than 1, n is negative. 540, 000, 000 = 5. 4 x 1017

Let’s Practice Write in scientific notation: A. 2060 B. . 0036 C. 93, 000 Write in standard notation: D. 3. 0 x 104 E. 2. 3 x 102 F. 9. 1 x 10 -6 Answers: A. 2. 06 x 103 B. 3. 6 x 10 -3 C. 9. 3 x 107 D. 30, 000 E. 230 F. 0. 0000091

• Adding and Subtracting in Scientific Notation: – If the expression has the same exponent, add/subtract the M values and keep n the same. Example: (6 x 104 m) + (3. 2 x 104 m) = 9. 2 x 104 m – If the exponents differ, you need to make them the same before adding or subtracting M. • Hint: Convert the smaller exponent into the bigger one! Example: (5 x 108 kg) – (1. 3 x 107 kg) = (5 x 108 kg) – (. 13 x 108 kg) = 4. 87 x 108 kg

• Multiplying in Scientific Notation: – Values can be multiplied whether or not n is the same. • Multiply M and add n. (6 x 102 s) x (3 x 103 s) = 1. 8 x 106 s 2 • Dividing in Scientific Notation: – Values can also be divided whether or not n is the same. • Divide M and subtract n. (1. 0 x 105 m) = 4 x 101 m/s (2. 5 x 103 s)

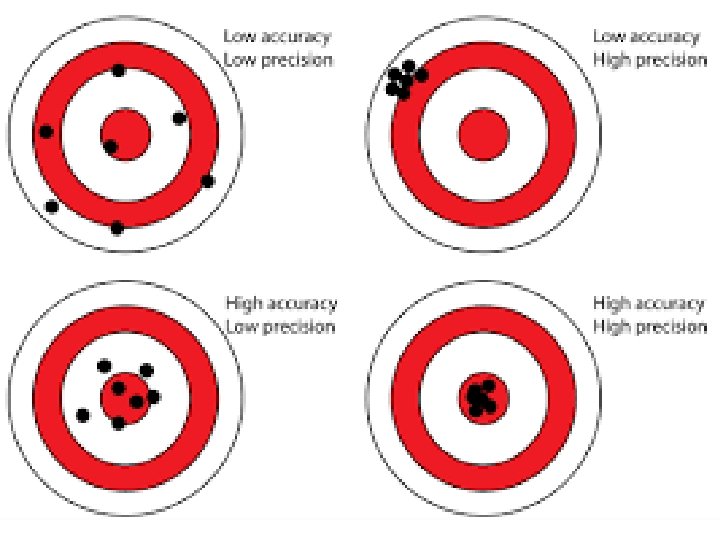
Accuracy, Precision, and Error • Accuracy and Precision • It is important that your measurements should be correct and reproducible. – We like to use the words accurate and precise. • Try to come up with a definition for these two words. • Hint:

• Accuracy is a measure of how close a measurement comes to the actual or true value of whatever is measured. • Precision is a measure of how close a series of measurements are to one another. • To evaluate the accuracy of a measurement, the measured value must be compared to the correct value. To evaluate the precision of a measurement, you must compare the values of two or more repeated measurements. BACK TO THE TARGETS!

• Determining Error: • Individual measurements may be accurate or inaccurate, due to many possible factors. • Example: – You use a thermometer to measure the boiling point of pure water at standard pressure. The thermometer reads 99. 1 o. C. You know that the boiling point of pure water is supposed to be 100. 0 o. C. • There is a clear error here and we need to figure out how inaccurate the measurement is. • There is a difference between the accepted value, which is the correct value based on reliable references, and the experimental value, the value measured in the lab.

• There is a difference between the accepted value, which is the correct value based on reliable references, and the experimental value, the value measured in the lab. – The difference between the accepted value and the experimental value is called the error. Error = Experimental Value – Accepted Value • It is also useful to be able to calculate relative, or percent error. – Percent error is the absolute value of the error divided by the accepted value, multiplied by 100%. Percent Error = |Error| accepted value x 100%

• Example: – Using thermometer example from two slides back, this is how we would compute: G: Exp. Value = 99. 1 o. C Acc. Value = 100. 0 o. C U: % Error Eq: Sol: |99. 1 o. C-100 o. C| 100 o. C x 100% = 0. 9%

Practice Problem:

Answers to Practice Problems: 1. G: Ex val. : 11. 9 g/m. L Acc. Val. : 19. 3 g/m. L Sol: |11. 9 -19. 3| 19. 3 x 100% = 38. 3% 2. G: Ex. Val. : 8. 75 g/m. L Acc. Val. : 8. 71 g/m. L Sol: |8. 75 -8. 71| 8. 71 x 100% =. 459% U: Eq: U: Eq. : % Error

• Significant Figures in Measurement: – Let’s say you are at the store and want to buy some produce. That is usually sold at a cost per pound. You want to make sure that you don’t have too much, so you use the scale nearby to check. – What does this read?

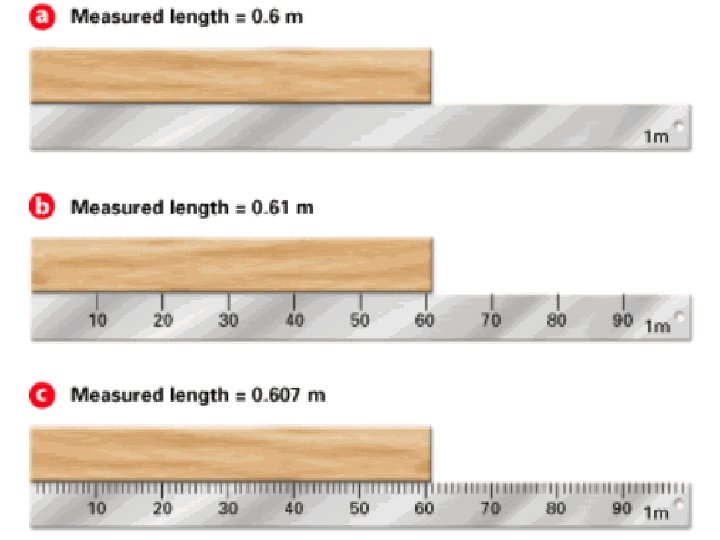
• On the scale, you can see that it can measure to the nearest ounce. However, you can also see that you can estimate one more digit to get a more precise reading. • You may only see 8 lbs, 10 oz, but when you look carefully, it actually reads 8 lbs, 9. 9 oz. – Every bit of that measurement conveys useful information, so all of those digits are significant, even the estimated one. • These are called significant figures. • Significant figures in a measurement include all of the digits that are known, plus the last digit that is estimated. • Measurements must always be reported to the correct number of significant figures because calculated answers often depend on the number of significant figures in the values used in the calculation. • Why do significant figures matter? – Measurements are only as accurate as the least precise number.

Significant Figures • Rules: 1. Nonzero digits are significant 2. Final zeros used after a decimal point are significant. 3. Zeros between two other significant digits are always significant. 4. Zeros used solely for spacing the decimal point are not significant.

Significant Figures in Calculations: • In general, a calculated answer cannot be more precise than the least precise measurement from which it was calculated. • Rounding: – Once you know the number of significant figures your answer should have, round to that many digits, counting from the left.

• Adding and Subtracting: – When adding and subtracting, do the math first. – Next, determine which measurement was the least precise. – The answer should be rounded to the same number of decimal places (not digits) as the least precise measurement. Example: 12. 52 349. 0 + 8. 24 369. 76 The second measurement, 349. 0 is the least precise, the answer should be rounded to the nearest tenth. Actual answer: 369. 8

• Multiplication and Division: – Do the math first. • Remember that multiplying and dividing influences the units too! – Determine which measurement had the fewest significant figures. – Round your answer to have the same number of significant figures as the measurement that had the least. Example: 7. 55 m x 0. 34 m = 2. 567 m 2 Since 0. 34 has 2 sig. figs. (fewest), the answer should only have 2. Answer: 2. 6 m 2

Quick. Lab (~10 -15 min. )

1. 2. 3. 4. 5. 6. 7. Learning Checkpoint: How do measurements relate to experimental science? How are accuracy and precision evaluated? Why must a given measurement always be reported to the correct number of significant figures? How does the precision of a calculated answer compare to the precision of the measurements used to obtain it? A technician experimentally determined the boiling point of octane to be 124. 1 o. C. The actual boiling point of octane is 125. 7 o. C. Calculate the error and the percent error. Determine the number of significant figures in each of the following. A. 11 soccer players B. 0. 070 020 meters C. 10, 800 meters D. 5. 00 cubic meters Solve the following and express each answer in scientific notation and to the correct number of significant figures. A. (5. 3 x 104 m) + (1. 3 x 104 m) B. (7. 2 x 10 -4 m) / (1. 8 x 103 s) C. (9. 12 x 10 -1 kg) – (4. 7 x 10 -2 kg) D. (5. 4 x 104 m) x (3. 5 x 109 m)

3 -2 The International System of Units Learning Target: To be fluent within the metric system. Success Criteria: I can… • list SI units of measurement and common SI prefixes. • distinguish between the mass and weight of an object. • convert between the Celsius and Kelvin temperature scales.

3 -2 The International System of Units Introduction: • If you are traveling on a family vacation in another country and see a sign that says “Dalby 211” on it, you may realize that Dalby is still a distance away. Unfortunately, you don’t know exactly how far, since there is no unit provided. • When you make a measurement, you need to assign a unit of measurement to the numerical value. – This makes it possible to communicate the measurement in a clear way to others.

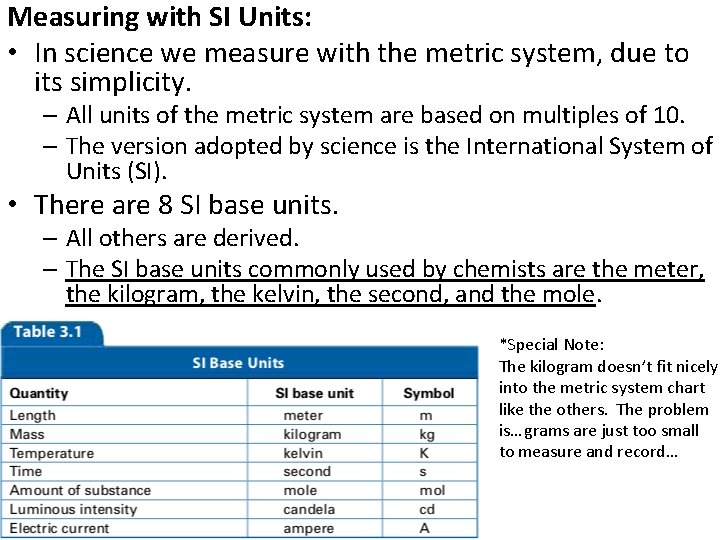
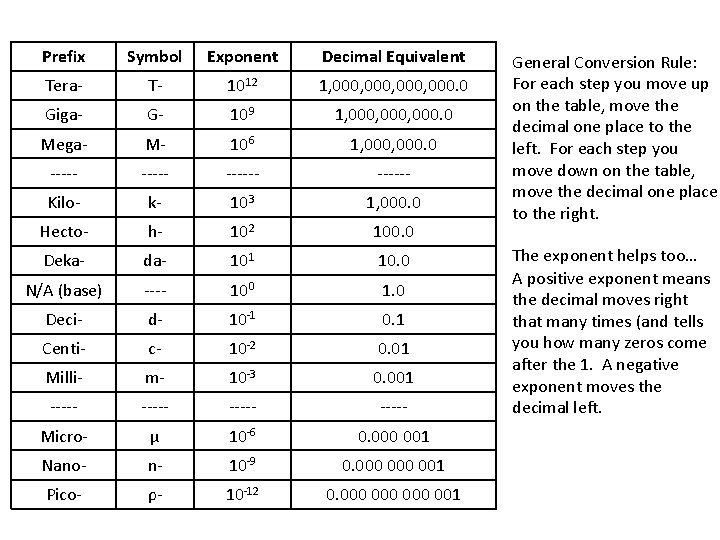
Measuring with SI Units: • In science we measure with the metric system, due to its simplicity. – All units of the metric system are based on multiples of 10. – The version adopted by science is the International System of Units (SI). • There are 8 SI base units. – All others are derived. – The SI base units commonly used by chemists are the meter, the kilogram, the kelvin, the second, and the mole. *Special Note: The kilogram doesn’t fit nicely into the metric system chart like the others. The problem is… grams are just too small to measure and record…

Prefix Symbol Exponent Decimal Equivalent Tera- T- 1012 1, 000, 000. 0 Giga- G- 109 1, 000, 000. 0 Mega- M- 106 1, 000. 0 ------ Kilo- k- 103 1, 000. 0 Hecto- h- 102 100. 0 Deka- da- 101 10. 0 N/A (base) ---- 100 1. 0 Deci- d- 10 -1 0. 1 Centi- c- 10 -2 0. 01 Milli- m- 10 -3 0. 001 ----- Micro- μ 10 -6 0. 000 001 Nano- n- 10 -9 0. 000 001 Pico- ρ- 10 -12 0. 000 000 001 General Conversion Rule: For each step you move up on the table, move the decimal one place to the left. For each step you move down on the table, move the decimal one place to the right. The exponent helps too… A positive exponent means the decimal moves right that many times (and tells you how many zeros come after the 1. A negative exponent moves the decimal left.

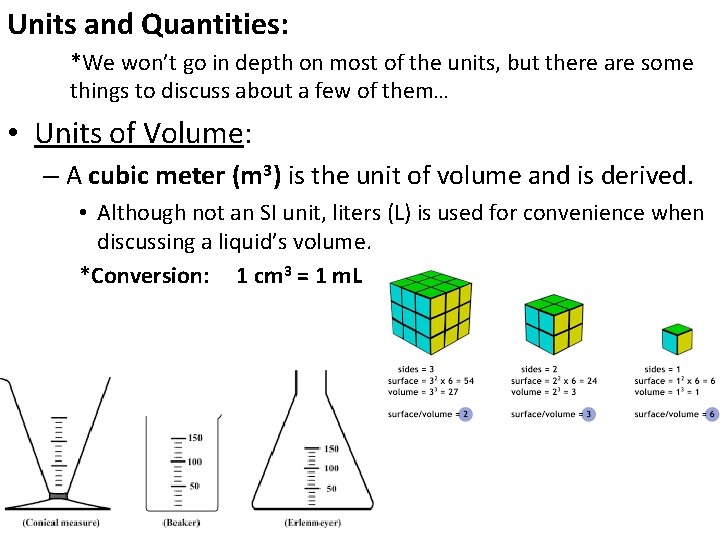
Units and Quantities: *We won’t go in depth on most of the units, but there are some things to discuss about a few of them… • Units of Volume: – A cubic meter (m 3) is the unit of volume and is derived. • Although not an SI unit, liters (L) is used for convenience when discussing a liquid’s volume. *Conversion: 1 cm 3 = 1 m. L

• Units of Volume (cont. ): • There are many devices used to measuring liquid volumes: – Erlenmeyer Flask – Buret – Graduated Cylinder – Beaker – Volumetric Flask

• Units of Mass: • To measure mass, we use the triple beam balance. • Mass is a bit goofy, because although the base in the metric system chart would be grams, kilograms is the technical base of the SI system. – This is due to the realistic tendency that most things in the universe have large masses. • Weight vs Mass… What’s the difference? – Mass is a measure of quantity of matter. – Weight is a force that measures the pull on a given mass by gravity. • Weight can change from location to location, but mass will not.

• Units of Temperature: • Temperature is a measure of the average kinetic energy of the particles in a sample of matter. – Some would say it is a measure of how hot or cold an object is. – Heat moves from an object with higher temperature to one with a lower temperature. • Because almost all (except water) substances expand when heated and contract when cooled, liquids are used to help a thermometer work.

• Temperature (cont. ): • Scientists commonly use two equivalent units of temperature, the degree Celsius and the kelvin. – The Celsius scale sets the freezing point of water at 0 o. C and the boiling point of water at 100 o. C • The distance between is divided into 100 equal parts. – On the Kelvin scale, the freezing point of all matter is set at 0 kelvins (K). • This is known as absolute zero. – Conversions: Since one degree Celsius is equivalent to one kelvin, the conversion equation is: K = o. C + 273

Practice Problems: • Liquid nitrogen boils at 77. 2 K. What is this temperature in degrees Celsius? • The element silver melts at 960. 8 o. C and boils at 2212 o. C. Express these temperatures in kelvins.

• Units of Energy: • Energy is the capacity to do work or to produce heat. • The joule and the calorie are common units of energy. • The joule (J) is the SI unit of energy. – One calorie (cal) is the quantity of heat that raises the temperature of 1 g of pure water by 1 o. C. • Conversion: 1 cal = 4. 184 J

Learning Checkpoint: 1. Which metric units are commonly used to measure length, volume, mass, temperature, and energy? 2. What is the symbol and meaning of each prefix? 1. milli- 2. nano- 3. deci- 4. centi- 3. List the following units in order from largest to smallest: m 3, m. L, μL, L, d. L. 4. What is the volume of a paperback book 21 cm tall, 12 cm wide, and 3. 5 cm thick? 5. State the difference between mas and weight. 6. State the relationship between degrees Celsius and kelvins. 7. Surgical instruments may be sterilized by heating at 170 o. C for 1. 5 hr. Convert 170 o. C to kelvins. 8. State the relationship between joules and calories.

3 -3 Conversion Problems Learning Targets: -To learn how to convert within the metric system. -To learn how to use dimensional analysis. Success Criteria: I can… 1. Construct conversion factors from equivalent measurements. 2. Apply the technique of dimensional analysis to a variety of conversion problems. 3. Solve problems by breaking the solution into steps. 4. Convert complex units using dimensional analysis.

3 -3 Conversion Factors • Think about a number from an everyday situation. Can it be expressed in more than one way? – Are there other ways to represent a dollar in such a way that you could pay people back with it? 1 dollar = 2 half-dollars = 4 quarters = 10 dimes = 20 nickels = 100 pennies.

• Whenever two measurements are equivalent, a ratio of the two measurements will equal 1. – A conversion factor is a ratio of equivalent measurements. – In the above conversion, since these number/unit combinations all mean the same thing, they cancel out to 1. – Notice that the smaller number is always part of the measurement with the larger unit.

• When a measurement is multiplied by a conversion factor, the numerical value is generally changed, but the actual size of the quantity measured remains the same.

Dimensional Analysis: Tutorial Video Here • Several great approaches, including basic algebra, can be used to solve problems, but one of the best is dimensional analysis. – Dimensional analysis is a way to analyze and solve problems using the units, or dimensions, of measurements. – Dimensional analysis provides you with an alternative approach to problem solving.

Converting Between Units: • Of course the “metric z” is helpful when you are first learning the metric system, but it is not the best way and has its limitations. • Problems in which a measurement with one unit is converted to an equivalent measurement with another unit are easily solved using dimensional analysis.

• You may not always be able to use nice conversions like we just saw. – We may need to use exponents, rather than regular numbers… Let’s take a short-cut! Just combine the ratios

Let’s solve these without using the metric z. Don’t do 33. c. right now…

• Converting Complex Units: • This one will require multiple steps… • If I am driving 1. 00 x 102 km/h, how fast am I driving in m/s? 100 km/h x (1000 m/1 km) x (1 h/3600 s)= 27. 77777 = 27. 8 m/s (we had to adjust for significant figures…

Learning Checkpoint 1. What happens to the numerical value of a measurement that is multiplied by a conversion factor? What happens to the actual size of the quantity? 2. Why is dimensional analysis useful? 3. What types of problems can be solved with dimensional analysis? 4. Make the following conversions. A. 14. 8 g to μg B. 3. 72 x 10 -3 kg to g C. 66. 3 L to cm 3 5. An atom of gold has a mass of 3. 721 x 10 -22 g. How many atoms of gold are in 5. 00 g of gold? 6. Light travels at a speed of 3. 00 x 1010 cm/s. What is the speed of light in km/h?

3 -4 Density Learning Targets: To understand what determines the density of a substance. To know how a change in temperature affects density. Success Criteria: I can… 1. calculate the density of a material from experimental data. 2. describe how density varies with temperature.

3 -4 Density Determining Density: • What is density? – Density is the ratio of the mass of an object to its volume. ** Equation** ρ = Density (kg/m 3, but is usually written in g/cm 3) m= mass (g) V= volume (cm 3)

Let’s try it… • A 10. 0 cm 3 piece of lead has a mass of 114 g. What is lead’s density? • ρ = m/v = 114/10. 0 = 11. 4 g/cm 3.

Try These!!! 1. A student finds a shiny piece of metal that she thinks is aluminum. In the lab, she determines that the metal has a volume of 245 cm 3 and a mass of. 612 kg. Calculate the density. If aluminum has a density of 2. 70 g/cm 3, is this sample made of aluminum? 1. What is the volume of a pure silver coin that has a mass of 14 g? The density of silver (Ag) is 10. 5 g/cm 3.

• Density is an intensive property that depends only on the composition of a substance, not on the size of the sample. – With a mixture, density can vary because the composition of a mixture can vary. • This is how phases (layers) can exist in a suspension. • Objects with less density will float in those with higher densities. • In general, the density of a substance decreases as its temperature increases.

Learning Checkpoint! 1. What determines the density of an object? 2. How does density cary with temperature? 3. A weather balloon is inflated to a volume of 2. 2 x 103 L with 37. 4 g of helium. What is the density of helium in g/cm 3? 4. A 68 g gold bar is cut into 3 equal pieces. How does the density of each piece compare to the density of the original gold bar? 5. A plastic ball with a volume of 19. 7 cm 3 has a mass of 15. 8 g. Would this ball sink or float in a container of gasoline (density of gas is. 66 g/cm 3)? 6. What is the volume, in cubic centimeters, of a sample of cough syrup that has a mass of 50. 0 g? The density of cough syrup is 0. 950 g/cm 3.