Scientific Measurement Chapter 2 Sections 2 3 Measuring

Measuring • Using the equipment at your lab table make the following measurements: 25

SI Units The International System of Units Measurement SI Unit Symbol Length Meter m

Unit Prefixes Prefix Symbol Example Relationship to base unit Mega M Mm – Megameter

Scientific Notation • Scientific notation is a formal method of applying large numbers and

More Examples and helpful hints • When numbers are very large, make them smaller

$More Examples and helpful hints • When numbers are very small and represent fractions$

Accuracy versus Precision • Taking good measurements requires good instruments and limited human error.

Accuracy versus Precision • Accuracy describes the ability to reproduce the same measurements based

Measuring • Which measurements from the previous slide were the most precise? • Which

Rules for Significant Digits • Leading zeros are not significant Ex: 0. 0000345 •

Rules for Significant Digits • Measurements that are used as definitions will always have

Rounding • In addition and subtraction you must round your answer to the lowest

Rounding • When multiplying/dividing you must round your answer to the least number of

Rounding • We look to the original problem and check the number of significant

Slides: 18

Download presentation

Scientific Measurement Chapter 2 Sections 2 & 3

Measuring • Using the equipment at your lab table make the following measurements: 25 m. L using a graduated cylinder 25 m. L using a beaker 19 cm using a ruler 19 cm using a meter stick 5 grams on a triple beam balance 5 grams on a digital scale

SI Units The International System of Units Measurement SI Unit Symbol Length Meter m Mass Kilogram kg Volume Liter L Time Second s Temperature Kelvin K Density Kilograms/meter³ kg/m³ Amount of substance Mole mol

Unit Prefixes Prefix Symbol Example Relationship to base unit Mega M Mm – Megameter 1, 000 x larger Kilo k kg – kilogram 1000 x larger Deca D DL – decaliter 10 x larger Base Unit m, l, s Meter, liter, second, gram, etc. Deci d dm – decimeter 10 x smaller or 0. 1 Centi c cm – centimeter 100 x smaller or 0. 01 Milli m m. L - milliliter 1000 x smaller or 0. 001 Micro μ μL – microliter 1, 000 x smaller Nano n ns – nanosecond 1, 000, 000 x smaller Pico p pm – picometer 1, 000, 000 x smaller

Scientific Notation • Scientific notation is a formal method of applying large numbers and very small numbers to a base ten (10) format. Ex. 1000 = 1 x 10³ or 2350 = 2. 350 x 10³ • For whole numbers the decimal at the end is understood • For fractional numbers the decimal is at the beginning

More Examples and helpful hints • When numbers are very large, make them smaller by “moving” the understood decimal to the left and multiplying by base 10 raised to some exponent. • The exponent will be positive in the number of decimal places moved • Ex. 1, 623, 400 becomes 1. 6234 x

$More Examples and helpful hints • When numbers are very small and represent fractions$

More Examples and helpful hints • When numbers are very small and represent fractions of whole numbers, make them larger by “moving” the decimal to the right and multiplying by base ten (10) raised to some exponent. • The exponent will be negative in the number of places the decimal moved. • Ex. 0. 000235 becomes 2. 35 x

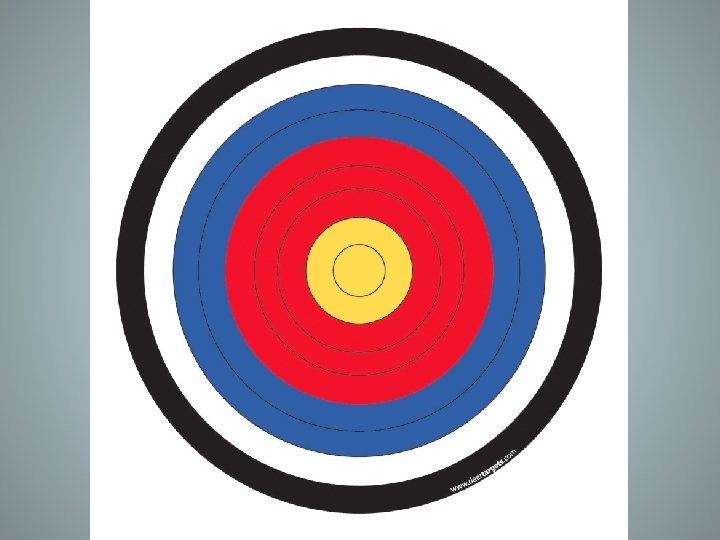
Accuracy versus Precision • Taking good measurements requires good instruments and limited human error. • Precision describes the ability to reproduce the same measurement using the same scale and instruments • These arrows are precise

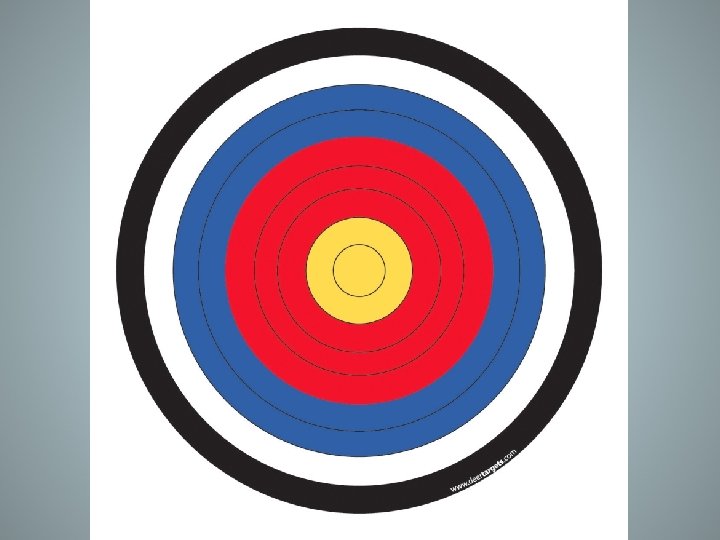
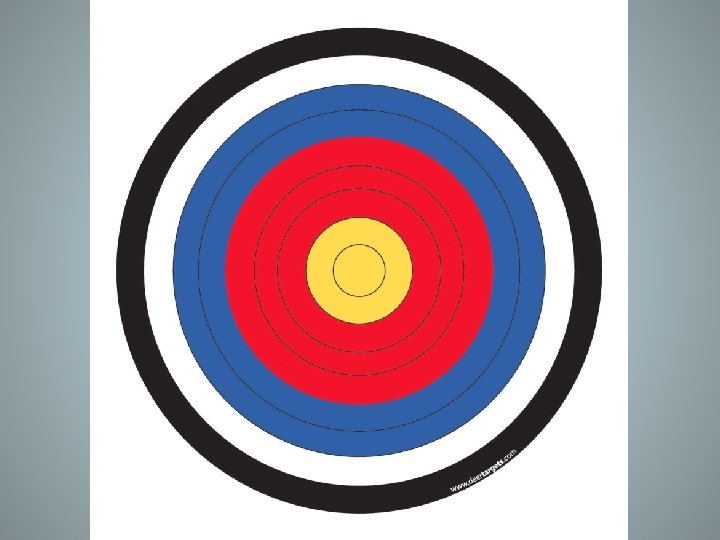
Accuracy versus Precision • Accuracy describes the ability to reproduce the same measurements based upon an actual “tested” or “accepted” value • These arrows are accurate because they are close to the center, not necessarily each other

Measuring • Which measurements from the previous slide were the most precise? • Which were the most accurate? • Who at your table came closest to the value given?

Rules for Significant Digits • Leading zeros are not significant Ex: 0. 0000345 • Imbedded zeros are always significant Ex: 1. 2000068 • Trailing zeros are only significant if the decimal is present (after the decimal) Ex: 628. 000

Rules for Significant Digits • Measurements that are used as definitions will always have unlimited significant zeros Ex: 1 meter = 100 centimeters 1 Liter = 1000 milliliters • Measurements that are a result of counting numbers will always have unlimited zeros Ex: 25 students or 7 lab tables

Rounding • In addition and subtraction you must round your answer to the lowest number of decimal places in the numbers added/subtracted Ex: 3. 76 g + 14. 83 g + 2. 1 g = 20. 69 g = 20. 7 g • We look to the original problem to see the number of decimal places shown in each of the original measurements. • 2. 1 shows the least number of decimal places We must round our answer, 20. 69, to one decimal place (the tenth place). Our final answer is 20. 7 g

Rounding • When multiplying/dividing you must round your answer to the least number of significant figures given in the numbers you are multiplying/dividing • Ex: 22. 37 cm x 3. 10 cm x 85. 75 cm = 5946. 50525 cm 3 • Our answer can only show 3 significant digits because that is the least number of significant digits in the original problem.

Rounding • We look to the original problem and check the number of significant digits in each of the original measurements: 1. 22. 37 shows 4 significant digits 22. 37 cm 2. 3. 10 shows 3 significant digits 3. 10 cm 3. 85. 75 shows 4 significant digits 85. 75 cm Our final answer becomes 5950 cm 3