Scientific Data Tables Graphs Equations and Math What

Scientific Data …Tables, Graphs, Equations and Math?
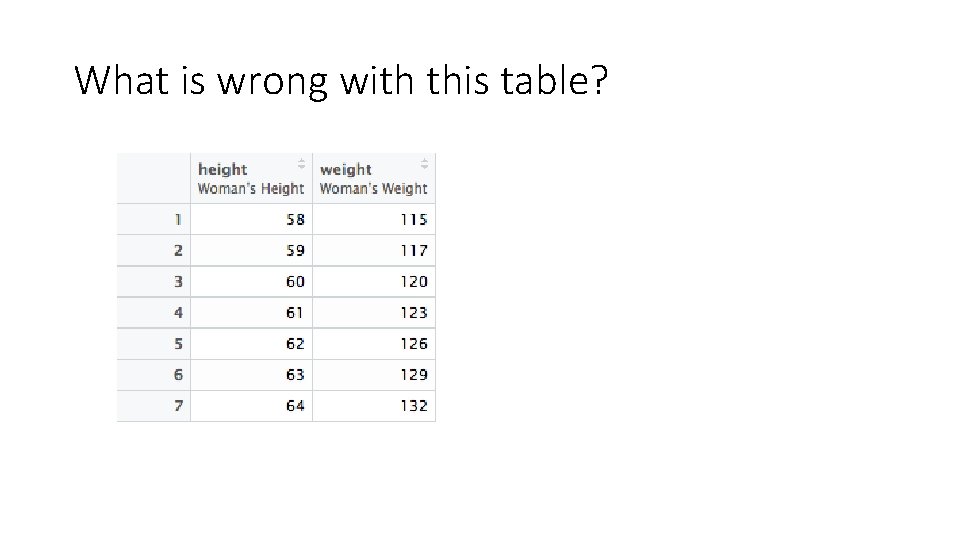
What is wrong with this table?

What was the independent variable in this experiment?
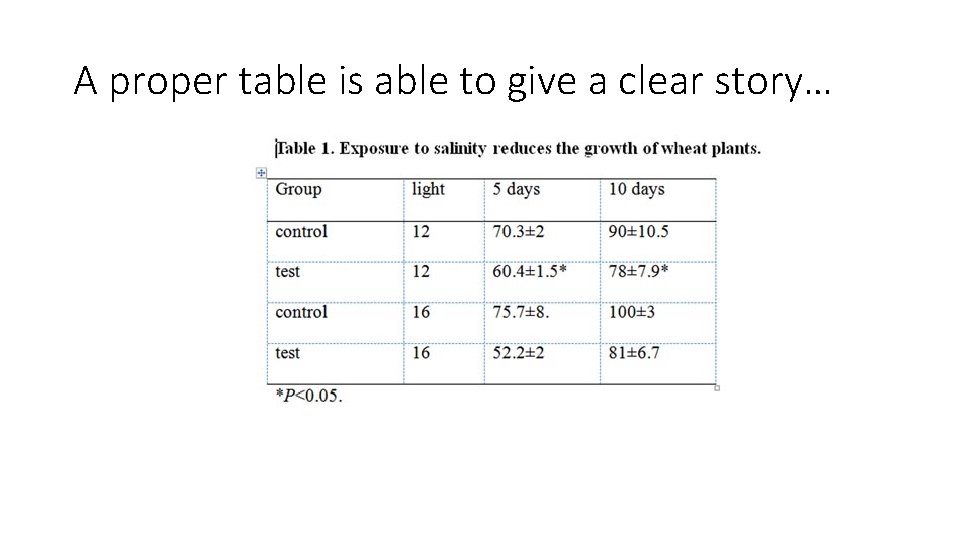
A proper table is able to give a clear story…

Excellent Tables… • Usually… • • Independent variable(s) is recorded in the first column Dependent variable(s) is recorded in the subsequent column(s). The number of observations taken determines the number of rows. Contain a title explaining what is shown in the table.

What is wrong with this graph?
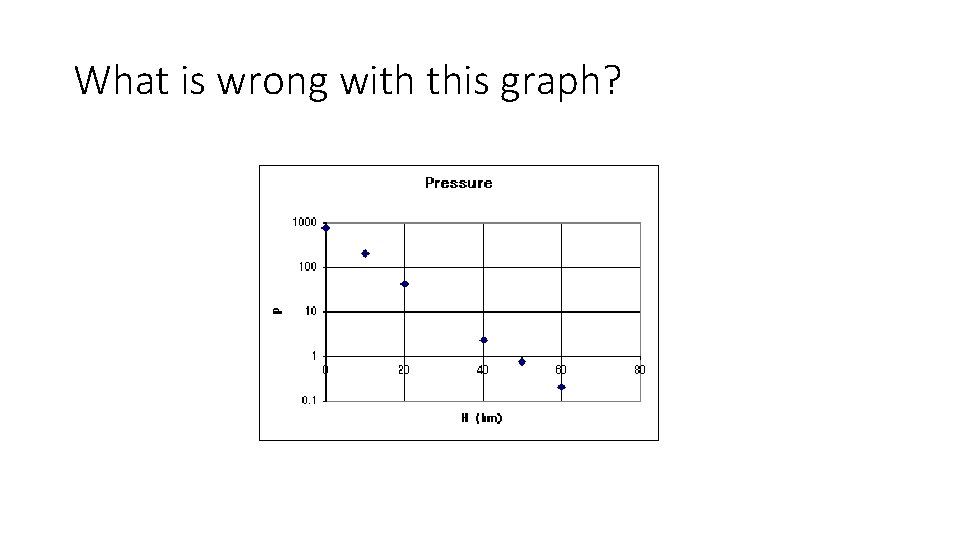
What is wrong with this graph?
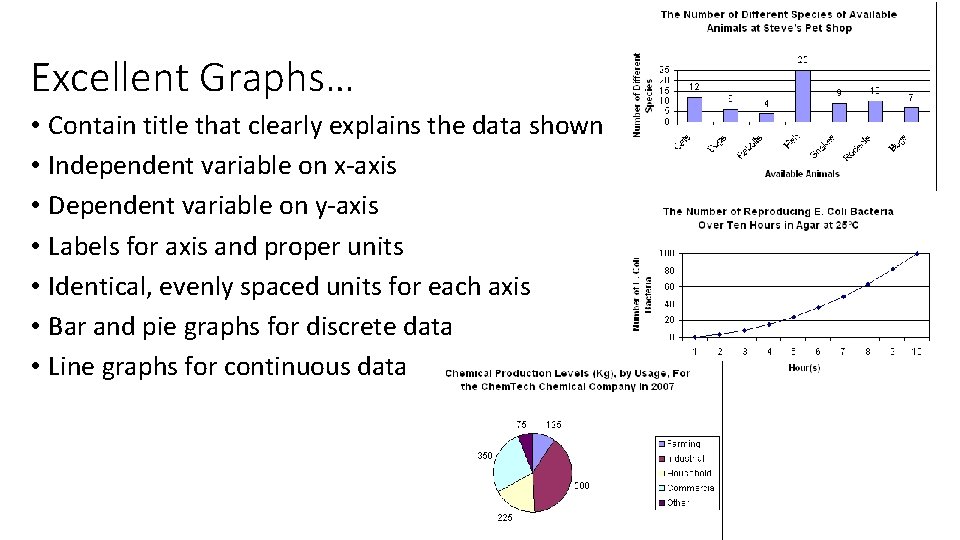
Excellent Graphs… • Contain title that clearly explains the data shown • Independent variable on x-axis • Dependent variable on y-axis • Labels for axis and proper units • Identical, evenly spaced units for each axis • Bar and pie graphs for discrete data • Line graphs for continuous data
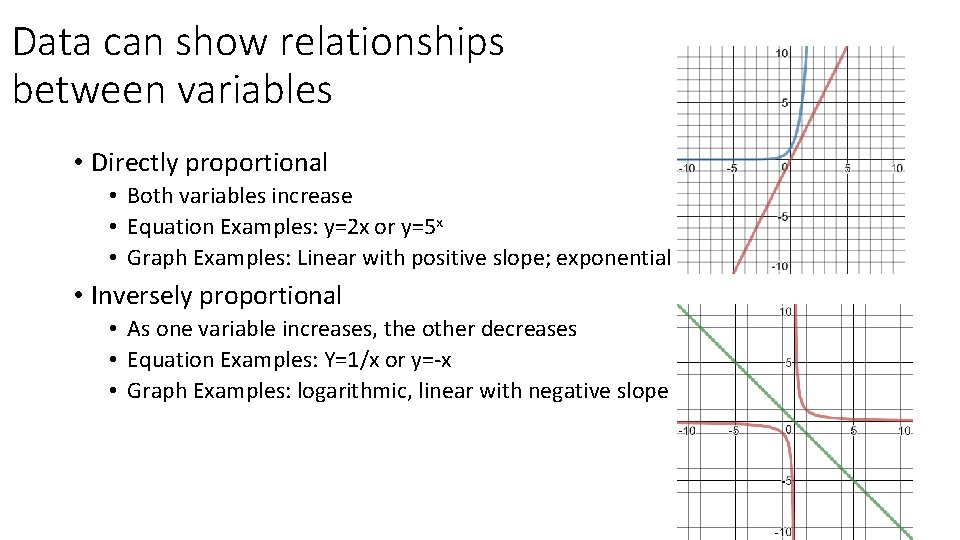
Data can show relationships between variables • Directly proportional • Both variables increase • Equation Examples: y=2 x or y=5 x • Graph Examples: Linear with positive slope; exponential • Inversely proportional • As one variable increases, the other decreases • Equation Examples: Y=1/x or y=-x • Graph Examples: logarithmic, linear with negative slope
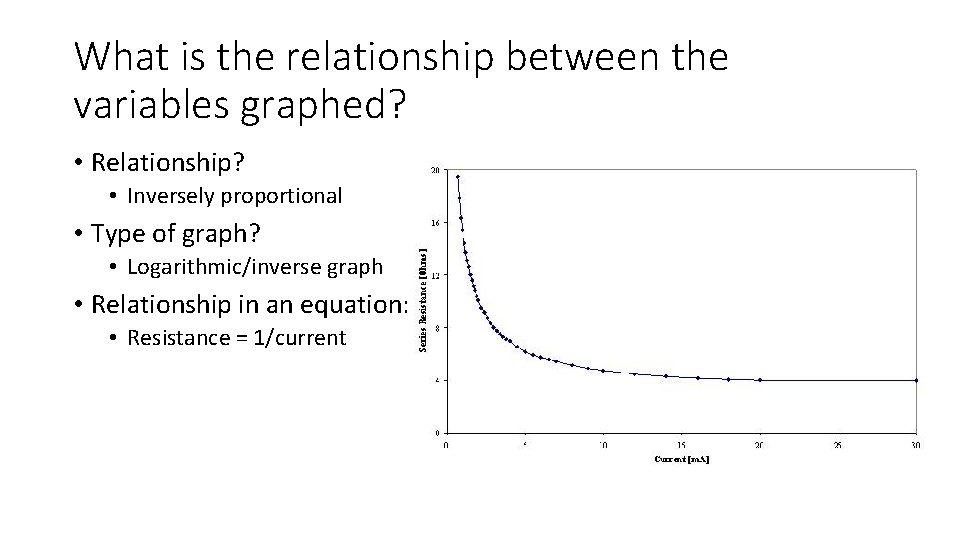
What is the relationship between the variables graphed? • Relationship? • Inversely proportional • Type of graph? • Logarithmic/inverse graph • Relationship in an equation: • Resistance = 1/current
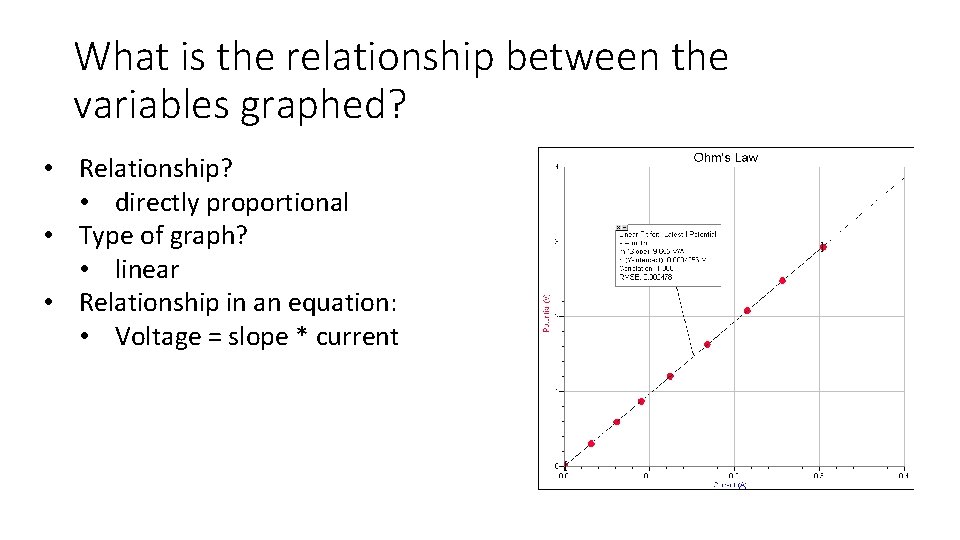
What is the relationship between the variables graphed? • Relationship? • directly proportional • Type of graph? • linear • Relationship in an equation: • Voltage = slope * current
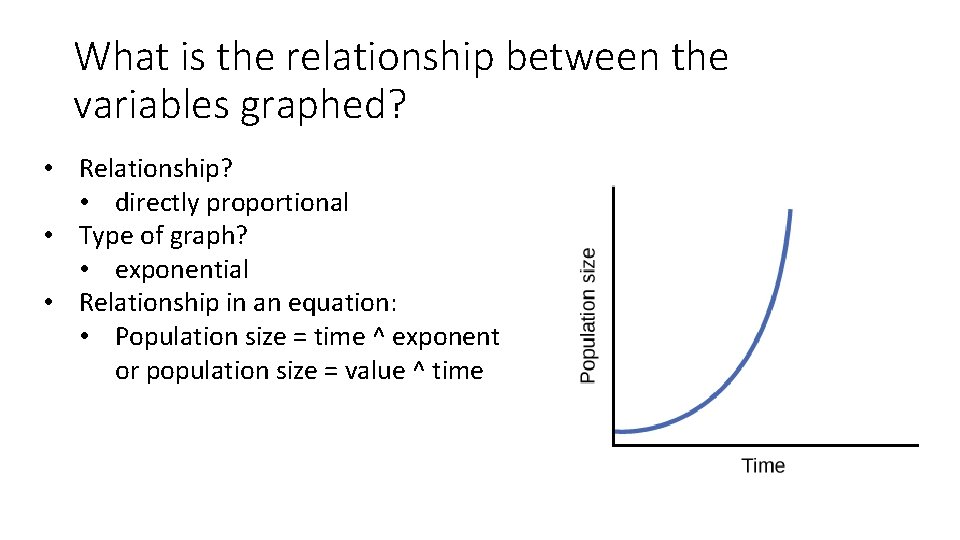
What is the relationship between the variables graphed? • Relationship? • directly proportional • Type of graph? • exponential • Relationship in an equation: • Population size = time ^ exponent or population size = value ^ time
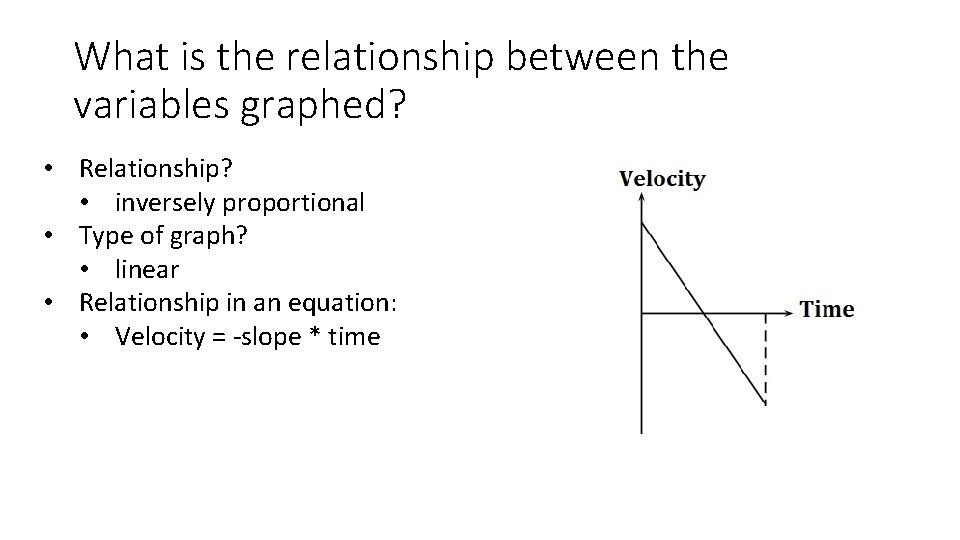
What is the relationship between the variables graphed? • Relationship? • inversely proportional • Type of graph? • linear • Relationship in an equation: • Velocity = -slope * time
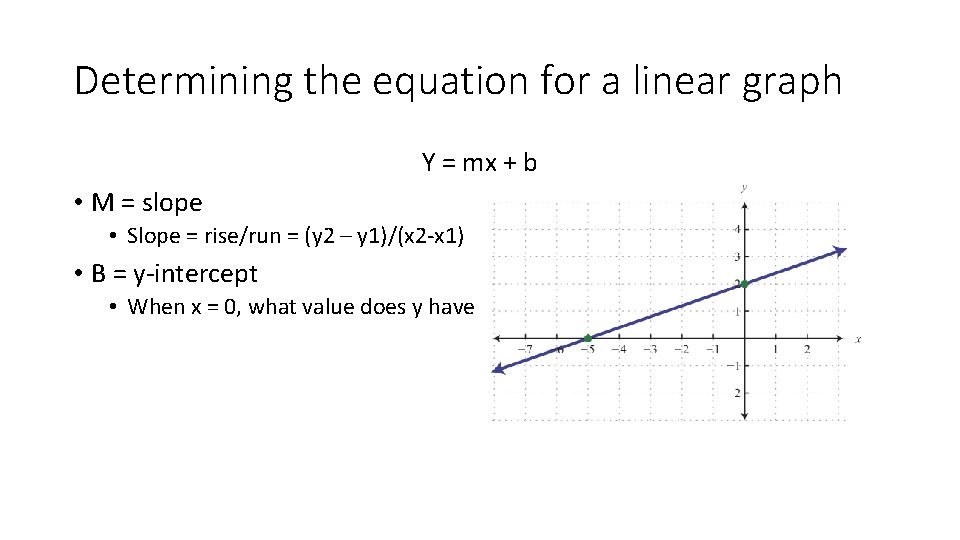
Determining the equation for a linear graph Y = mx + b • M = slope • Slope = rise/run = (y 2 – y 1)/(x 2 -x 1) • B = y-intercept • When x = 0, what value does y have
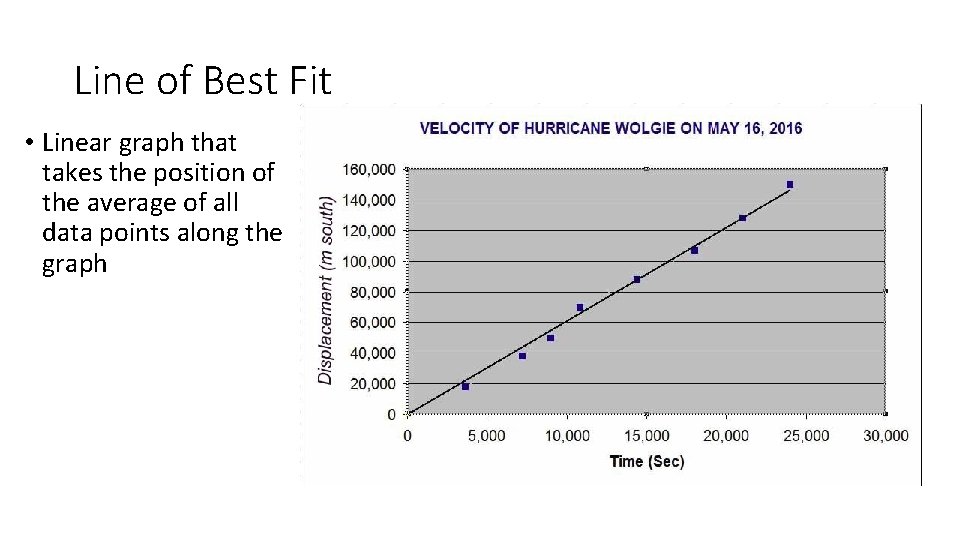
Line of Best Fit • Linear graph that takes the position of the average of all data points along the graph
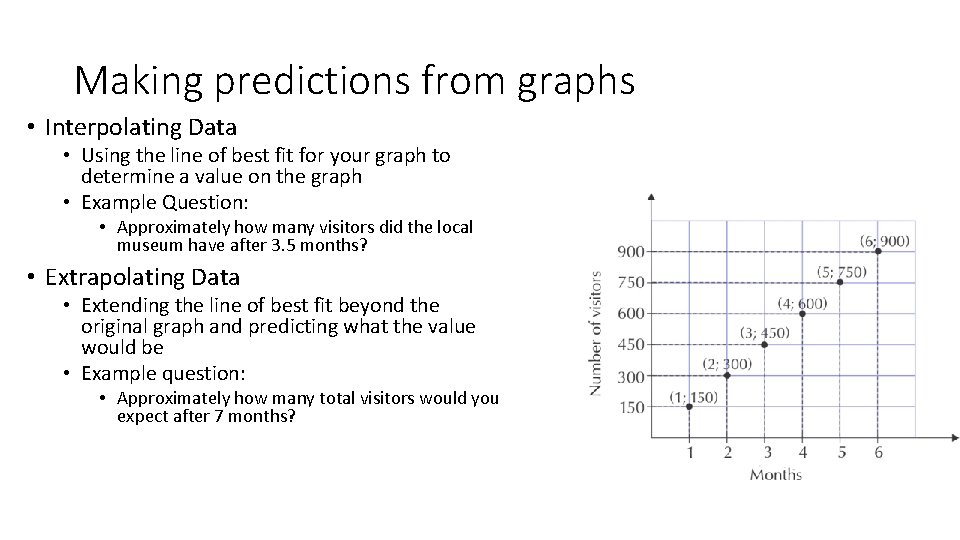
Making predictions from graphs • Interpolating Data • Using the line of best fit for your graph to determine a value on the graph • Example Question: • Approximately how many visitors did the local museum have after 3. 5 months? • Extrapolating Data • Extending the line of best fit beyond the original graph and predicting what the value would be • Example question: • Approximately how many total visitors would you expect after 7 months?

Other ways of interpreting data… • Range: difference between maximum and minimum data values • Median: middle value of a data set in numerical order • If even number of values in data set, take the average of the two middle values • Mode: most frequently observed value in the data set • Average/Mean: add together all the values and divide by the total number of values in the data set • Percent error: value that expresses how far from an actual value you are; smaller numbers mean you are more accurate in your experiment

How good are you at interpreting data? • What is the range of the data set? • What is the mode of the data set? • What is the median of the data set? • What is the mean of the data set? • The students who measured the temperature on Sunday made a major mistake; the actual temperature was 76°F. What was the student’s percent error?
- Slides: 18