Scientific Computing with Radial Basis Functions C S

Scientific Computing with Radial Basis Functions C. S. Chen Department of Mathematics University of Southern Mississippi U. S. A.

PURPOSE OF THE LECTURE TO SHOW RADIAL BASIS FUNCTIONS (RBFs) CAN BE USED TO PROVIDE 'MESH-FREE' METHODS FOR THE NUMERICAL SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS. 2021/9/17 2
2021/9/17 3

MESH METHOD 2021/9/17 MESHLESS METHOD 4

Advantages of Meshless Methods • It requires neither domain nor surface discretization. • The formulation is similar for 2 D and 3 D problems. • It does not involve numerical integration. • Ease of learning. • Ease of coding. • Cost effectiveness due to the man-power reduction involved for the meshing. 2021/9/17 5

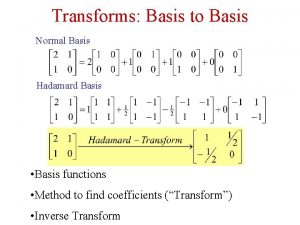
Radial Basis Functions Linear: Cubic: Multiquadrics: Polyharmonic Spines: Gaussian: 2021/9/17 6

Compactly Supported RBFs References • Z. Wu, Multivariate compactly supported positive definite radial functions, Adv. Comput. Math. , 4, pp. 283 -292, 1995. • R. Schaback, Creating surfaces from scattered data using radial basis functions, in Mathematical Methods for Curves and Surface, eds. M. Dahlen, T. Lyche and L. Schumaker, Vanderbilt Univ. Press, Nashville, pp. 477 -496, 1995 • W. Wendland, Piecewise polynomial, positive definite and compactly supported RBFs of minumal degree, Adv. Comput. Math. , 4, pp 389396, 1995. 2021/9/17 7

Wendland’s CS-RBFs Define For d=1, For d=2, 3, F o r 2021/9/17 8
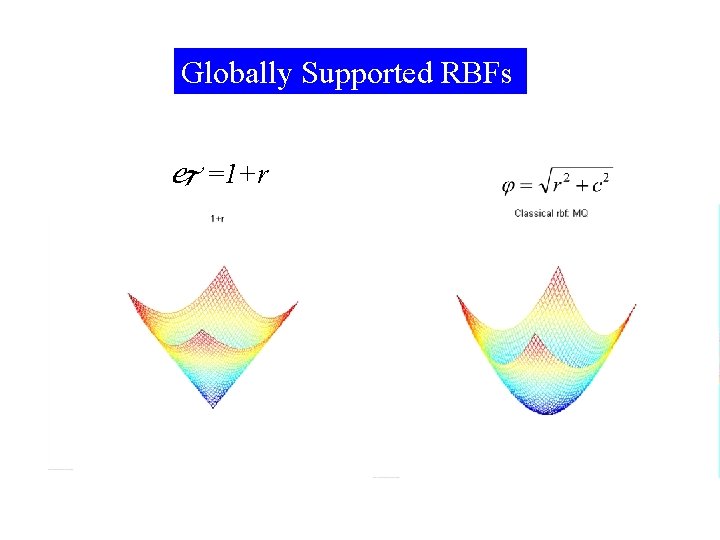
Globally Supported RBFs =1+r 2021/9/17 9

Compactly Supported RBFs 2021/9/17 10

Surface Reconstruction Scheme Assume that To approximate f by data set we usually require fitting the given of pairwise distinct centres with the imposed conditions The linear system is well-posed if the interpolation matrix is non-singular 2021/9/17 11
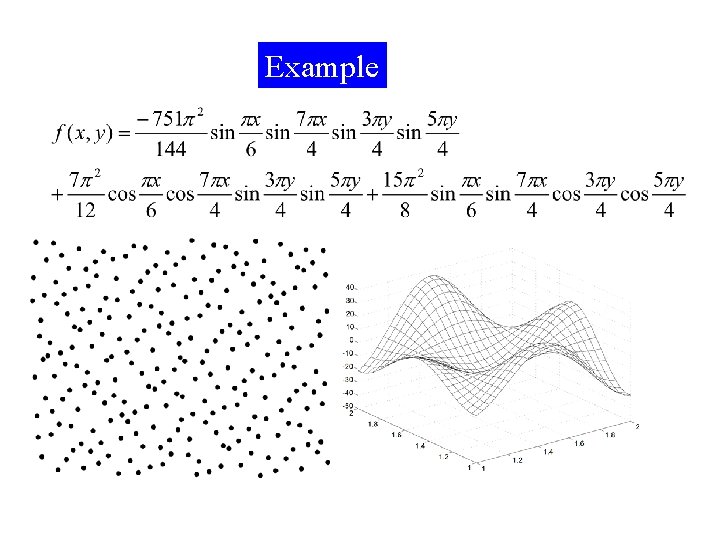
Example 2021/9/17 12

Meshless Method I Kansa’s Method or RBF Collocation Method 2021/9/17 13

RBF Collocation Method (Kansa’s Method) Consider the Poisson’s equation (1) (2) We approximate u by û by assuming (3) where 2021/9/17 14

(4) (5) By substituting (3), (5) into (1)-(2), we have (6) (7) can be obtained by solving N N system (6)-(7). 2021/9/17 15
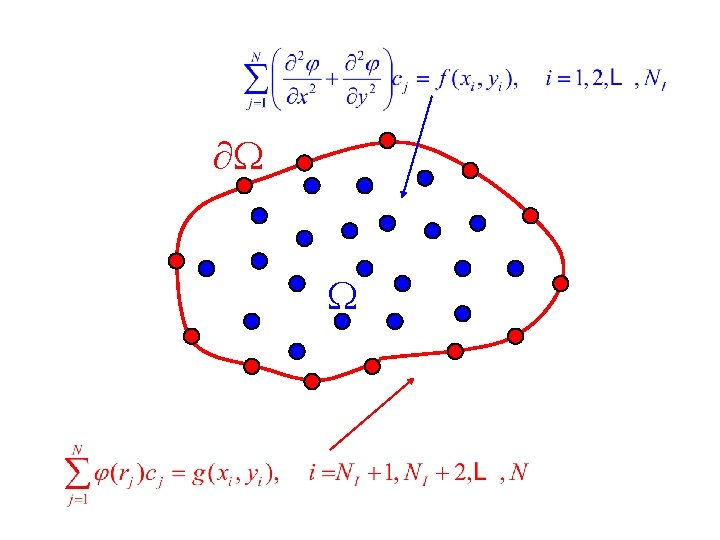
W W 2021/9/17 16

For parabolic problems such as heat equation, we have (8) where t is the time step, and un+1 are the solutions at time tn=n t and tn+1=(n+1) t. Similar to elliptic problems, we assume (9) 2021/9/17 17

Substituting (9) into (8) and (2), we have Notice that 2021/9/17 18

Example I where RBFs: MQ, c = 0. 8; i. e. , Grid points: 19 x 19 Maximum error: 8. 703 E-5 2021/9/17 19
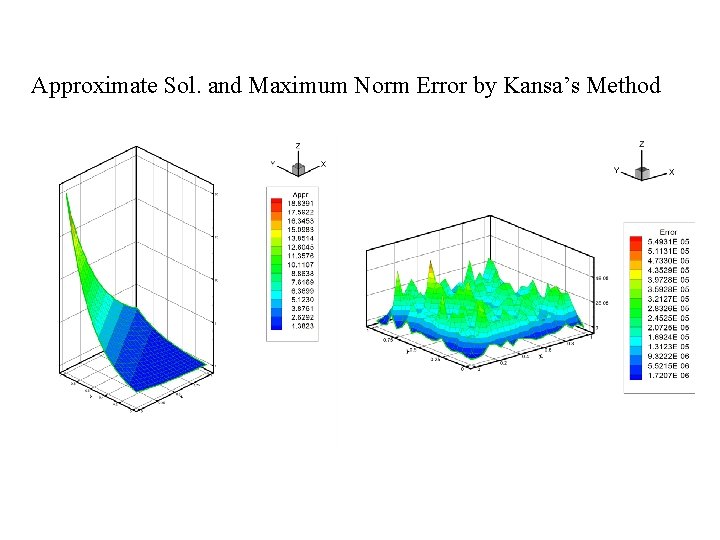
Approximate Sol. and Maximum Norm Error by Kansa’s Method 2021/9/17 20
![Example II (Rotating Cone) Exact solution: where t = 0. 01, t [0, 2] Example II (Rotating Cone) Exact solution: where t = 0. 01, t [0, 2]](http://slidetodoc.com/presentation_image_h2/b0b5cf6b7d9c7ea3a11c89bc31dde2da/image-21.jpg)
Example II (Rotating Cone) Exact solution: where t = 0. 01, t [0, 2] Maximum norm error = 0. 001165 with c = 0. 2 (MQ). 2021/9/17 21
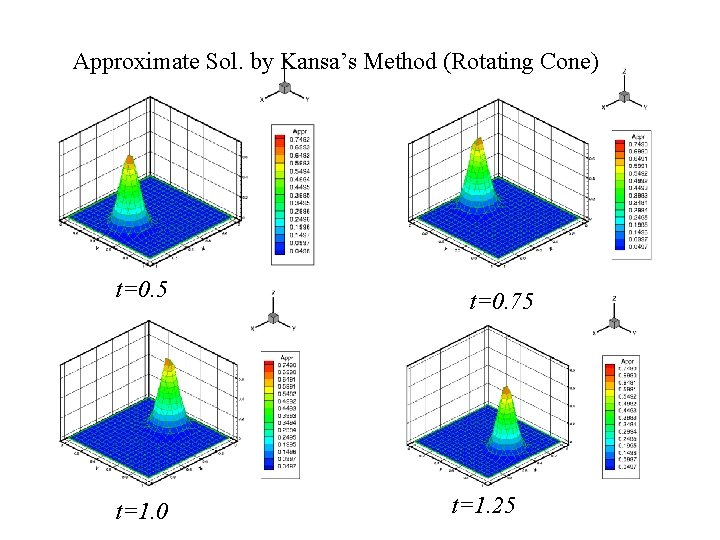
Approximate Sol. by Kansa’s Method (Rotating Cone) t=0. 5 2021/9/17 t=1. 0 t=0. 75 t=1. 25 22
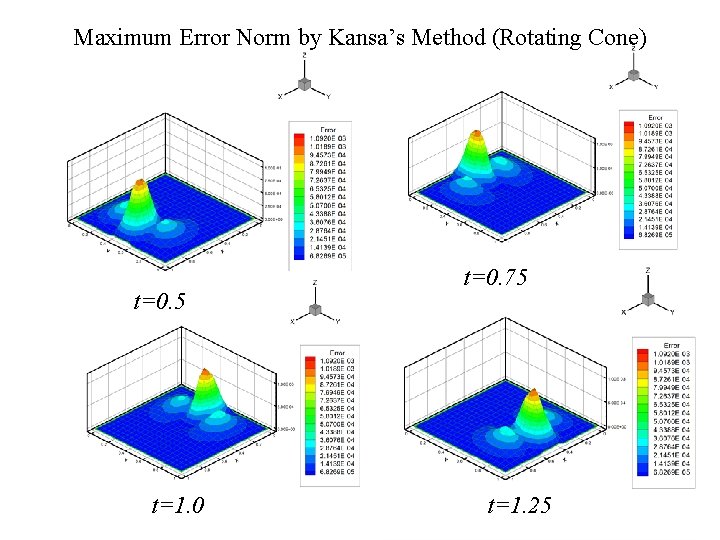
Maximum Error Norm by Kansa’s Method (Rotating Cone) t=0. 5 2021/9/17 t=1. 0 t=0. 75 t=1. 25 23
![Example III (Burgers’ Equation) Exact Solution t = 0. 01, t [0, 1. 25], Example III (Burgers’ Equation) Exact Solution t = 0. 01, t [0, 1. 25],](http://slidetodoc.com/presentation_image_h2/b0b5cf6b7d9c7ea3a11c89bc31dde2da/image-24.jpg)
Example III (Burgers’ Equation) Exact Solution t = 0. 01, t [0, 1. 25], = 0. 05 Maximum norm error = 0. 0719 with c = 0. 2 (MQ). 2021/9/17 24
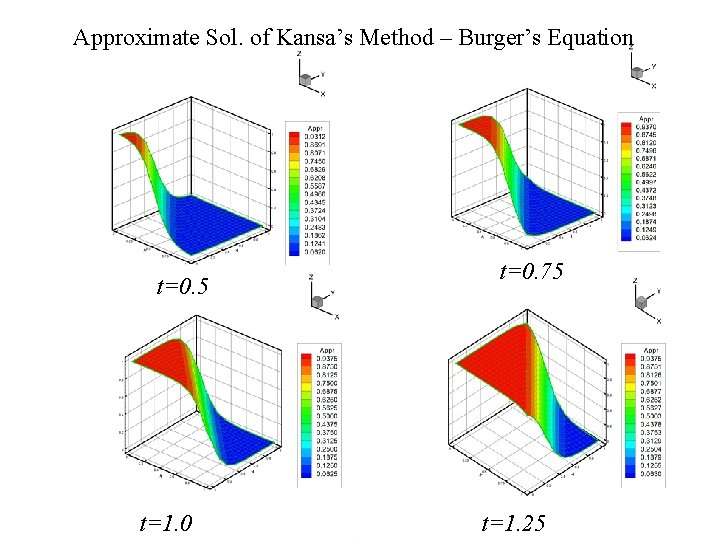
Approximate Sol. of Kansa’s Method – Burger’s Equation t=0. 5 2021/9/17 t=1. 0 t=0. 75 t=1. 25 25
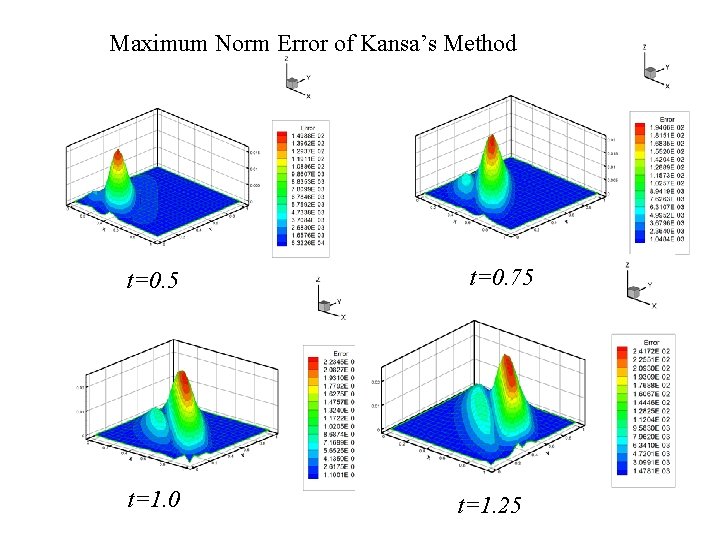
Maximum Norm Error of Kansa’s Method t=0. 5 2021/9/17 t=1. 0 t=0. 75 t=1. 25 26
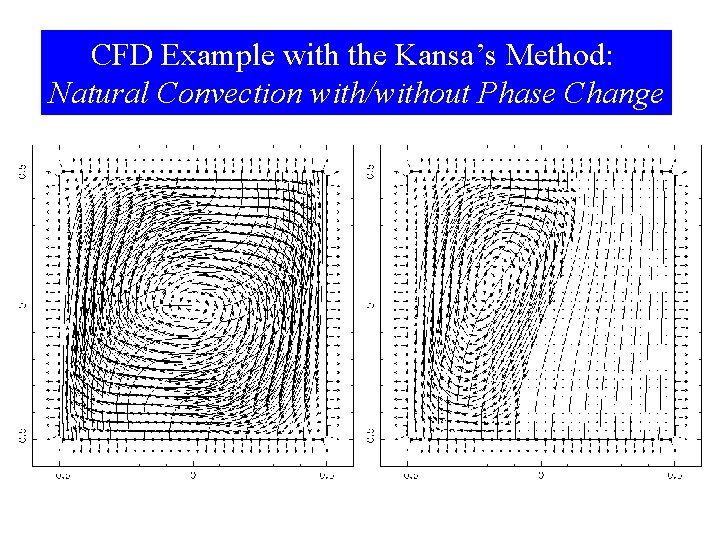
CFD Example with the Kansa’s Method: Natural Convection with/without Phase Change 2021/9/17 27

Meshless Method II MFS-DRM 2021/9/17 28

Elliptic PDEs 2021/9/17 29
WE FOCUS ON THIS *MFS - METHOD OF FUNDAMENTAL SOLUTIONS 2021/9/17 30

The Method of Fundamental Solutions Desingularized Method The Charge Simulation Method The Superposition Method Regular BEM 2021/9/17 31
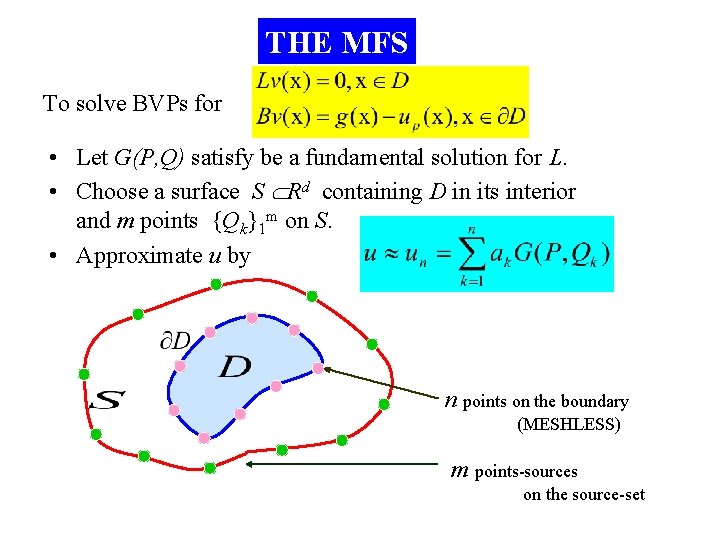
THE MFS To solve BVPs for • Let G(P, Q) satisfy be a fundamental solution for L. • Choose a surface S Rd containing D in its interior and m points {Qk}1 m on S. • Approximate u by n points on the boundary (MESHLESS) m points-sources 2021/9/17 on the source-set 32
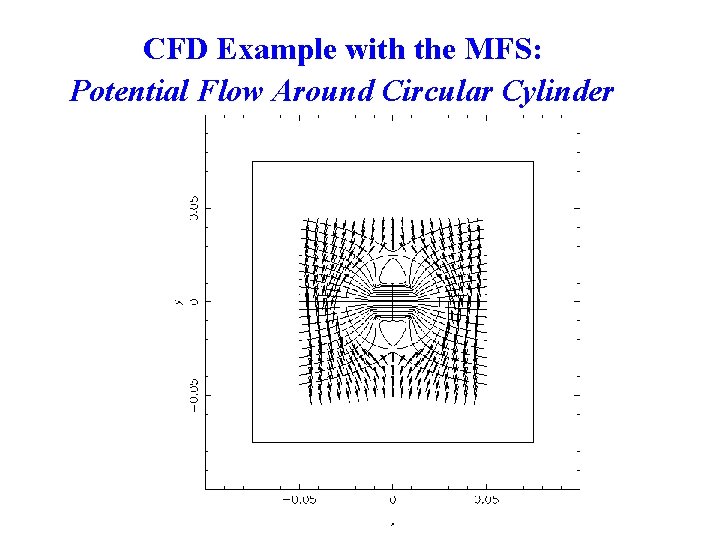
CFD Example with the MFS: Potential Flow Around Circular Cylinder 2021/9/17 33

MFS - SATISFYING BOUNDARY CONDITON To satisfy the boundary conditions one can use a variety of techniques • Galerkin’s Method (N. Limic, Galerkin-Petrov method for Helmholtz equation on exterior problems, Glasnik Mathematicki, 36, 245 -260, 1981) • Least Squares (G. Fairweather & A. Kargeorghis, The MFS for elliptic BVPs, Adv. Comp. Math. , 9, 69 -95, 1998) • Collocation (M. A. Golberg & C. S. Chen, The MFS for potential, Helmholtz and diffusion problems, Chapter 4, Boundary Integral Methods: Numerical and Mathematical Aspects, ed. M. A. Golberg, WIT Press and Computational Mechanics Publ. Boston, Southampton, 105 -176, 1999. ) 2021/9/17 34

COLLOCATION Choose n points on If B is linear, and set satisfy the linear equations A major concern with this method is the ill-conditioning of However, this generally does not affect accuracy. 2021/9/17 35

The Splitting Method Consider the following equation (10) (11) Where is a bounded open nonempty domain with sufficiently regular boundary Let where satisfying (12) but does not necessary satisfy the boundary condition in (11). v satisfies 2021/9/17 (13) (14) 36

Particular Solution • Domain integral • Atkinson’s method (C. S. Chen, M. A. Golberg & Y. C. Hon, The MFS and quasi-Monte Carlo method for diffusion equations, Int. J. Num. Meth. Eng. 43, 1421 -1435, 1998) (Requires no meshing if = circle or sphere) • Others 2021/9/17 37

Domain Embedding Method D 2021/9/17 38

Dual Reciprocity Method (DRM) Assume that and that we can obtain an analytical solution to (15) Then To approximate f by data set we usually require fitting the given of pairwise distinct centres with the imposed conditions 2021/9/17 39

The linear system (16) is well-posed if the interpolation matrix is non-singular (17) where (18) and 2021/9/17 40
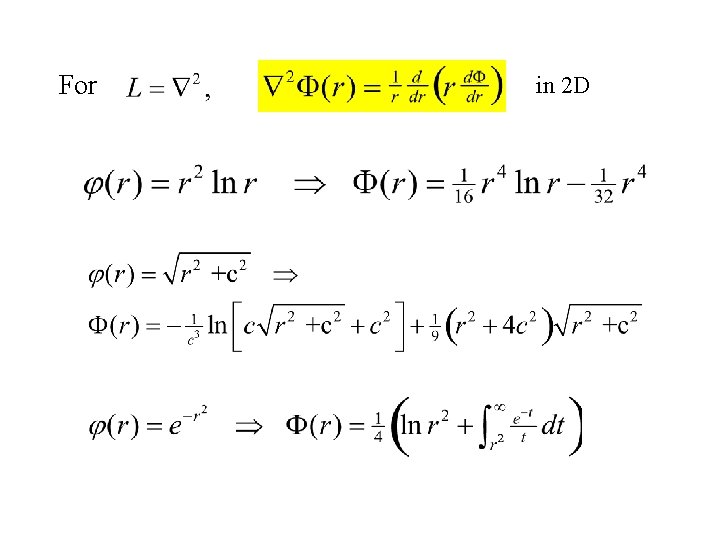
For 2021/9/17 in 2 D 41

Analytic Particular Solutions L= in 3 D Recall (19) Since we have 2021/9/17 42

Following the same integration procedure as above, we obtain (20) 2021/9/17 43
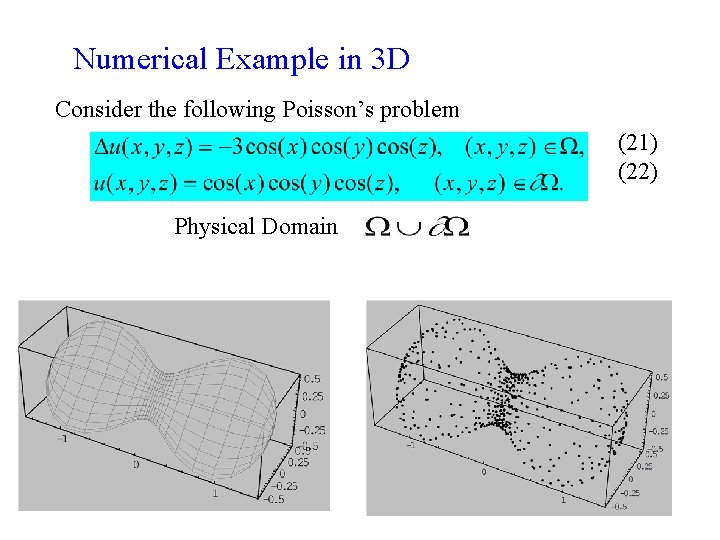
Numerical Example in 3 D Consider the following Poisson’s problem (21) (22) Physical Domain 2021/9/17 44
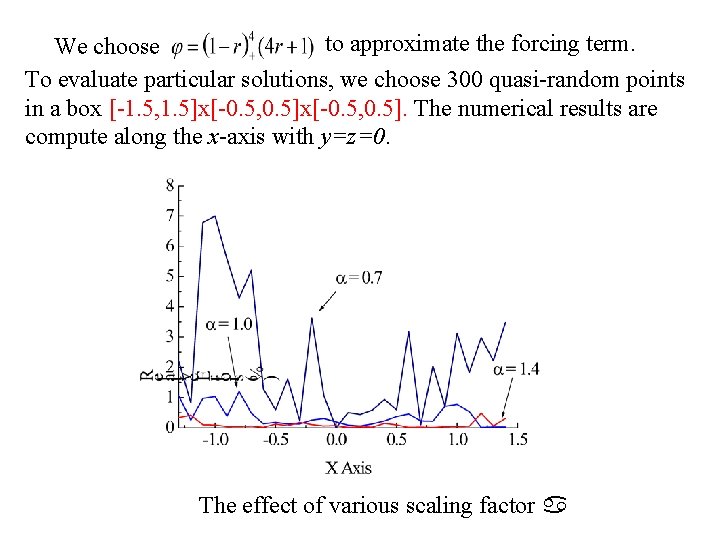
to approximate the forcing term. We choose To evaluate particular solutions, we choose 300 quasi-random points in a box [-1. 5, 1. 5]x[-0. 5, 0. 5]. The numerical results are compute along the x-axis with y=z=0. 2021/9/17 The effect of various scaling factor 45

RADIAL BASIS FUNCTION : POLYHARMONIC SPLINES • • M. A. Golberg, C. S. Chen & Y. F. Rashed, The annihilator method for Computing particular solutions to PDEs, Eng. Anal. Bound. Elem. , 23(3), 267274, 1999. A. Muleshkov, M. A. Golberg & C. S. Chen, Particular solutions of Helmholtztype operators using higher order polyharmonic splines, Computational Mechanics, 2000. (32) (33) where (34) 2021/9/17 46

Hence, to obtain approximate particular solutions to we approximate . By linearity, (37) Where the coefficients in (10) are chosen to guarantee maximal smoothness of 2021/9/17 47

For time-dependent problems, we consider two approaches to convert problems to Helmholtz equation • LAPLACE TRANSFORM • FINITE DIFFERENCES IN TIME ALSO POSSIBLE • OPERATOR SPLITTING (RAMACHANDRAN AND BALANKRISHMAN) 2021/9/17 48

(HEAT EQUATION) Consider the BVP (25) (26) (27) where D is a bounded domain in 2 D and 3 D. Let (28) 2021/9/17 (29) (30) 49

(WAVE EQUATION) Consider BVP (31) (32) (33) (34) (35) Similar approach can be applied to hyperbolic-heat equation and heat equations with memory 2021/9/17 50

(HEAT EQUATION) (36) (37) and (38) (39) (40) (41) 2021/9/17 51

http: //rbf-pde. uah. edu/ http: //www. cityu. edu. hk/ma/staff/ychon. html http: //www. num. math. uni-goettingen. de/schaback / http: //www. usm. edu/cschen 2021/9/17 52

The End 2021/9/17 53
- Slides: 53