Science 20 Unit B PHYSICS Chapter 1 Describing

Science 20 Unit B PHYSICS

Chapter 1: Describing Motion 1. 1 Average Speed 1. 2 New technologies 1. 3 Average Velocity 1. 4 & 1. 5 Graphing motion 1. 6 Calculating displacement 1. 7 & 1. 8 Stopping distance & braking 1. 9 Newton’s first law

Lesson 1. 1: Average Speed

What is uniform motion and nonuniform motion? l Uniform motion is motion in a straight line at a constant speed. – l Eg. ) a car traveling straight down a highway at 100 km/h Non-uniform motion is motion with a change in speed, direction or both. – Eg. ) a car slowing down or speeding up or turning around

What is average speed? l l Average speed is the distance (m or km) travelled over a specified time(s or h). Formula: average speed(m/s)=total distance(m) Means change in total time (s) v = d d t v t (see next slide)

km/h (km) (h)

Unit Conversions (see next slide) l Common conversions: 2 km x 1000 = ___ 2000 m Kilometer to meter: ___ l 2 Hours to seconds: ___ h x 3600 = 7200 ___ s l 120 s 2 min x 60 = ____ Minutes to seconds: ___ l 2 0. 6 km/h m/s: ___km/h x 1000 3600 = ___m/s l

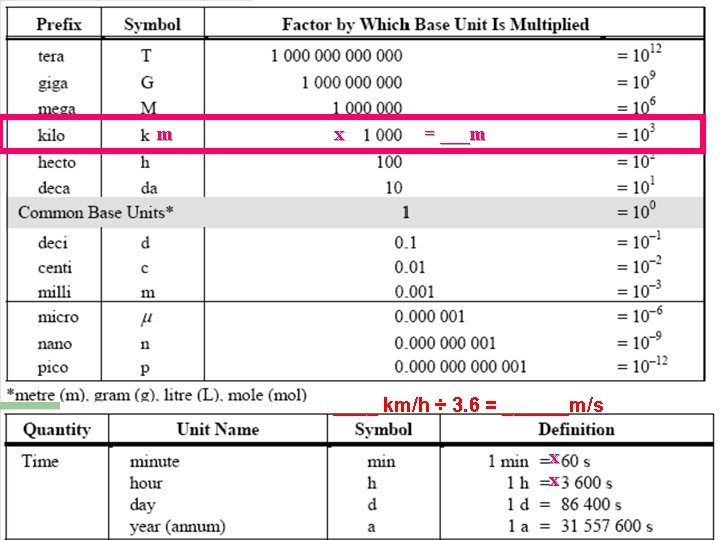
Example problem 1. 1 l Example: What is the speed of a cyclist that travels 40 km in 2. 5 h? – – l Step 1: Identify what you know and pick a formula d=40 km; t=2. 5 h; v=d/t Step 2: Substitute into the formula v = 40 m/2. 5 h (2 significant digits) Step 3: Solve v = 16 km/h (2 significant digits needed) Step 4: Use significant digits, units and a sentence The speed of the cyclist is 16 km/h. Try practice questions 1 – 3 on page 169

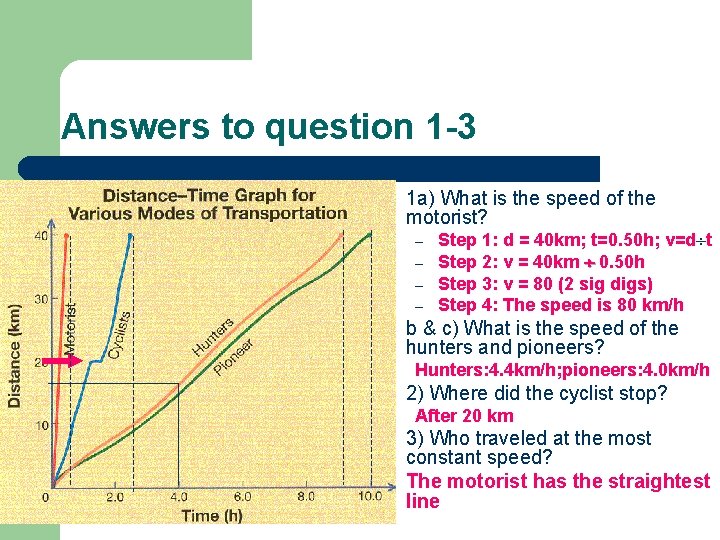
Answers to question 1 -3 l 1 a) What is the speed of the motorist? – – l Step 1: d = 40 km; t=0. 50 h; v=d t Step 2: v = 40 km 0. 50 h Step 3: v = 80 (2 sig digs) Step 4: The speed is 80 km/h b & c) What is the speed of the hunters and pioneers? Hunters: 4. 4 km/h; pioneers: 4. 0 km/h l 2) Where did the cyclist stop? After 20 km l 3) Who traveled at the most constant speed? The motorist has the straightest line

What is instantaneous speed, scalar quantities & vector quantities? l l l Instantaneous speed: Speed at an instant in time (eg) 40 km/h at this moment in time Scalar quantity: a quantity consisting of magnitude (amount) only, without direction. Eg) the speed is 100 km/h Vector quantity: a quantity consisting of magnitude (amount) and direction (north). Eg) the velocity is 100 km/h north

Example of scalars and vectors (pg 171 in text) l Scalars (no direction): – – – l Vectors(magnitude & direction): – l 284 m. L of Campbells soup 11. 89 on the VCR 20 C on thermometer 100. 3 FM on the radio 575 g of cereal 46 km & 117 km 15 km & 19 km to right Neither: – Highway 33 south (no magnitude is given)

d See What you Know Quiz v t 1. What is the equation for average speed? 2. What equation would you use to find d if v & t were given? 3. 100 km/h = ____ m/s? (use conversions to find the answer; how many meters are in 1 km, how many seconds are in one hour? ) 4. What is the difference between scalar and vector quantities? 5. Instantaneous speed is the _______ at an _______ in time.

d See What you Know Quiz v t 1. What is the equation for average speed? v = d/∆t 2. What equation would you use to find d if v & t were given? d = v * ∆t 3. 100 km/h = ____ m/s? (use conversions to find the answer; how many meters are in 1 km, how many seconds are in one hour? ) 100 km/h * 1000 m/1 km * 1 h/3600 s = 100 * 1000 / 3600 = 27. 8 m/s 4. What is the difference between scalar and vector quantities? Scalar: has magnitude/amount Vector: has magnitude & direction 5. Instantaneous speed is the speed at an instant in time.

Lesson 1. 2: Solving Problems with New Technologies

What are some technologies that have improved driving? l l l Soundproofing Suspension systems Power steering Halogen light bulbs Fuel efficient and fast engines

Example Problem 1. 3 l l During a sneeze, a driver’s eyes remain closed for 0. 50 s. If the car is moving at 100 km/h, km/h how far does the car move while the eyes are closed? SOLUTION: – – Step 1: t=0. 50 s; v=100 km/h x 1000 3600=27. 77 m/s; d=v t Step 2: d = 27. 77…m/s x 0. 50 s Step 3: d=13. 888 = 14 Step 4: The distance traveled is 14 m (about 3 car lengths) Try Practice Questions 9 & 10 on page 175

Q 8

Q 9 Q 9) It takes 2. 0 s to reach for a CD. a) If she is traveling 30 km/h what distance in meters does she travel. Step 1) v= 30 km/h x 1000/3600 = 8. 3333…m/s d=vt Step 2) d=8. 333 x 2. 0 s Step 3) d=16. 666666 Step 4) d = 17 m l

Example problem 1. 4 l l While traveling down a dark country road, the headlights allowed the driver to see 60 m. If the driver is traveling at 70 km/h, how many seconds will it take to reach the end of the headlight? SOLUTION: – – Step 1: d = 60 m; v=70 km/hx 1000 3600=19. 44…m/s; t= d v Step 2: t = 60 m 19. 44…m/s Step 3: t = 3. 08571; t=3. 1 Step 4: The time it would take is 3. 1 s Try Practice Problems 11 – 13 on page 176

Q 11 -13

Lesson 1. 3: Average Velocity

What are 3 vector measurements? l Position: Position a vector describing the location of an object relative to a reference point. – – l l Sign convention: an agreement about which direction is positive (north and east are positive) Try practice question 14 on page 180 Displacement ( d): a vector describing the change in length & direction of an object traveling in a straight line from a starting position. Average velocity( v): a vector describing the change in displacement over time. eg

How do you determine displacement? l A measurement from the starting point (r

Example problem 1. 5 l 5 cm=5 km [N] or + 5 km Melissa and Usha left 2. 0 hrs ago and travelled 5. 0 km from base camp. – – Use a ruler and the scale at the bottom of Figure B 1. 15 to identify where Melissa and Usha could be. Look at map to the right. - Scalzo or John Creek 5 cm=5 km[S] If Raj and Harvey want to join Melissa or – 5 km and Usha, what information other than the 5 km distance will they need? They need to know direction.

What is the head to tail method? What is the resultant? l l l Vectors can be drawn with arrows. The tail (start) and the head (end) of one arrow is labelled below. Tail 9 m (E) Head The head to tail method adds & subtracts vectors by using the head and tails of arrows. The resultant arrow is the arrow from the start to the end (head) of the last arrow drawn. start resultant arrow

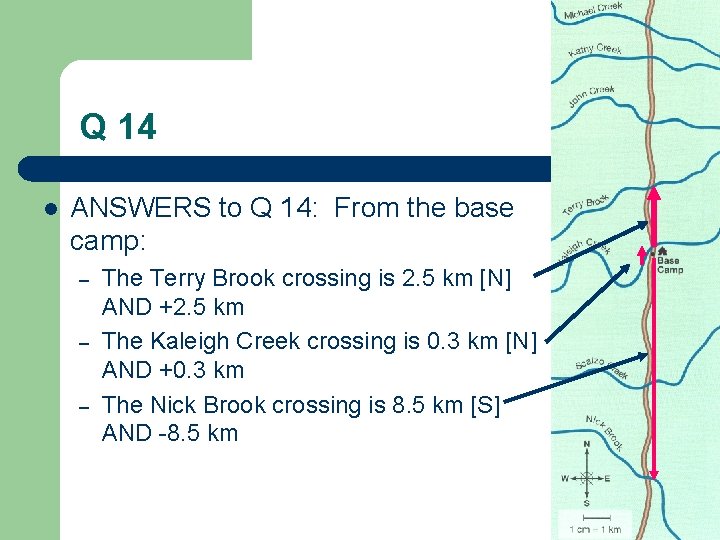
Q 14 l ANSWERS to Q 14: From the base camp: – – – The Terry Brook crossing is 2. 5 km [N] AND +2. 5 km The Kaleigh Creek crossing is 0. 3 km [N] AND +0. 3 km The Nick Brook crossing is 8. 5 km [S] AND -8. 5 km

Example problem 1. 6 Determine the displacement from the Michael Creek crossing to the Nick 17. 2 cm Brook crossing if it is 17. 2 cm south on the map and 1. 0 cm = 1. 0 km. l SOLUTION: d = 17. 2 km [S] or – 17. 2 km l Try practice problems 15 & 16 on page 181

Q 15 & 16 l l l 15 a)7. 5 km [N] AND +7. 5 km 15 b) 13. 5 km [N] AND + 13. 5 km 15 c) 5. 0 km [S] AND – 5. 0 km 15 d) 2. 5 km [N] AND + 2. 5 km 16) The answers are the same. They end up in the same place. b a c d

Comparing speed (scalar) and velocity (vector) l l Speed has the amount but no direction; therefore it is a scalar quantity Velocity has the amount and direction; it is a vector quantity

What is average velocity? l l Average velocity is the displacement (m or km w/direction) travelled over a specified time(s or h). Average velocity(m/s)[N] = displacement(m)[N] time (s) v = d d t v t

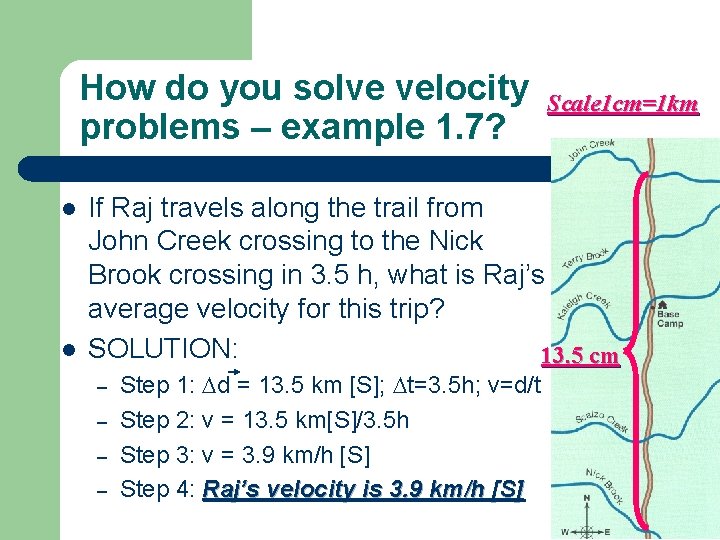
How do you solve velocity problems – example 1. 7? l l Scale 1 cm=1 km If Raj travels along the trail from John Creek crossing to the Nick Brook crossing in 3. 5 h, what is Raj’s average velocity for this trip? SOLUTION: 13. 5 cm – – Step 1: d = 13. 5 km [S]; t=3. 5 h; v=d/t Step 2: v = 13. 5 km[S]/3. 5 h Step 3: v = 3. 9 km/h [S] Step 4: Raj’s velocity is 3. 9 km/h [S]

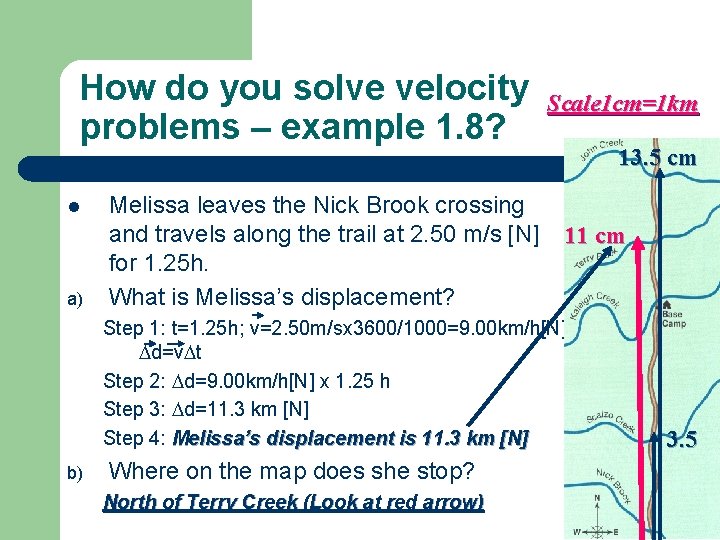
How do you solve velocity problems – example 1. 8? l a) Melissa leaves the Nick Brook crossing and travels along the trail at 2. 50 m/s [N] for 1. 25 h. What is Melissa’s displacement? Scale 1 cm=1 km 13. 5 cm 11 cm Step 1: t=1. 25 h; v=2. 50 m/sx 3600/1000=9. 00 km/h[N] d=v t Step 2: d=9. 00 km/h[N] x 1. 25 h Step 3: d=11. 3 km [N] Step 4: Melissa’s displacement is 11. 3 km [N] b) Where on the map does she stop? North of Terry Creek (Look at red arrow) 3. 5

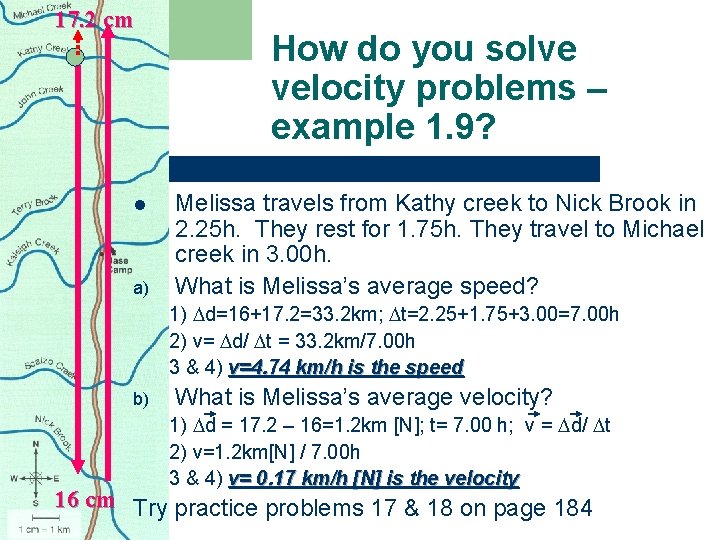
17. 2 cm l a) How do you solve velocity problems – example 1. 9? Melissa travels from Kathy creek to Nick Brook in 2. 25 h. They rest for 1. 75 h. They travel to Michael creek in 3. 00 h. What is Melissa’s average speed? 1) d=16+17. 2=33. 2 km; t=2. 25+1. 75+3. 00=7. 00 h 2) v= d/ t = 33. 2 km/7. 00 h 3 & 4) v=4. 74 km/h is the speed b) What is Melissa’s average velocity? 1) d = 17. 2 – 16=1. 2 km [N]; t= 7. 00 h; v = d/ t 2) v=1. 2 km[N] / 7. 00 h 3 & 4) v= 0. 17 km/h [N] is the velocity 16 cm Try practice problems 17 & 18 on page 184

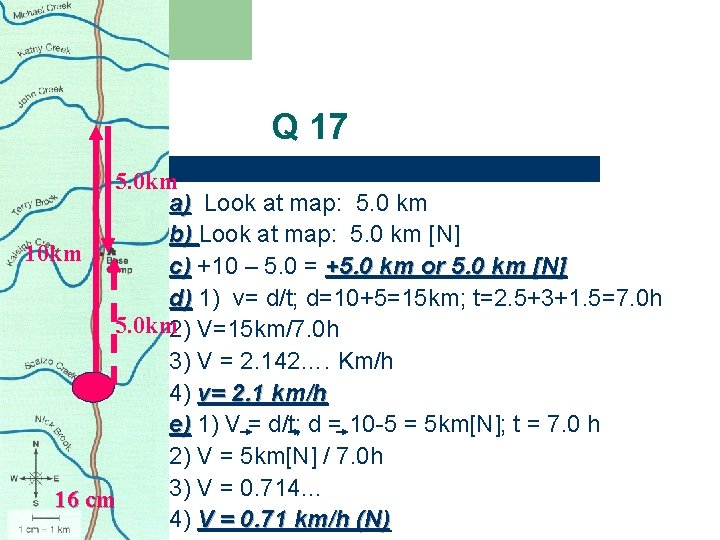
Q 17 5. 0 km a) Look at map: 5. 0 km b) Look at map: 5. 0 km [N] 10 km c) +10 – 5. 0 = +5. 0 km or 5. 0 km [N] d) 1) v= d/t; d=10+5=15 km; t=2. 5+3+1. 5=7. 0 h 5. 0 km 2) V=15 km/7. 0 h 3) V = 2. 142…. Km/h 4) v= 2. 1 km/h e) 1) V = d/t; d = 10 -5 = 5 km[N]; t = 7. 0 h 2) V = 5 km[N] / 7. 0 h 3) V = 0. 714… 16 cm 4) V = 0. 71 km/h (N)

1) scale d=1. 2 km[N] 4) resultant 1) start How do you find resultant displacement using scale diagram & head to tail method? 1. 2. 2) 1 st arrow 3) 2 nd arrow 3. 4. Place a dot to represent the starting point and pick a scale where 1 cm = __ Draw the first arrow (vector) from the starting point Start the next arrow (vector) at the head of the last arrow. Repeat step 3 for all the arrows. To find the resultant displacement, draw a dotted line from the starting point to the end of the last arrow.

See what you know quiz 1. 2. 3. 4. 5. What is the difference between speed and velocity? Rearrange the velocity formula to find displacement A person walks 5. 0 m [N] and 6. 0 m [S]. Sketch using arrows, his travels and determine the displacement. (Use head and tail method. ) Calculate the velocity of the person in Q 3 if it takes 10 s. Calculate the speed of the person in Q 3 if it takes

Lesson 1. 4 & 1. 5: Graphing uniform and accelerated motion

Computer models & crash test dummies in collisions l l l Models showing the stress on the eye during a collision help safety experts make appropriate safety equipment like soft air bags and padded sterring wheels Surgens use robots to perform microsurgery on the eye. A microscope is used because the parts of the eye are so small they need to be magnified. Try questions 19 & 20 on page 187

What information does a graph tell us about motion? l l l The slope of the line tells us information like velocity or acceleration (slope = rise = y 2 -y 1) run x 2 -x 1 The shape of the line tells us if we have constant uniform speed/velocity, acceleration or if the object has stopped The area under the graph can tell us the distance/displacement travelled. (Area = length x width)

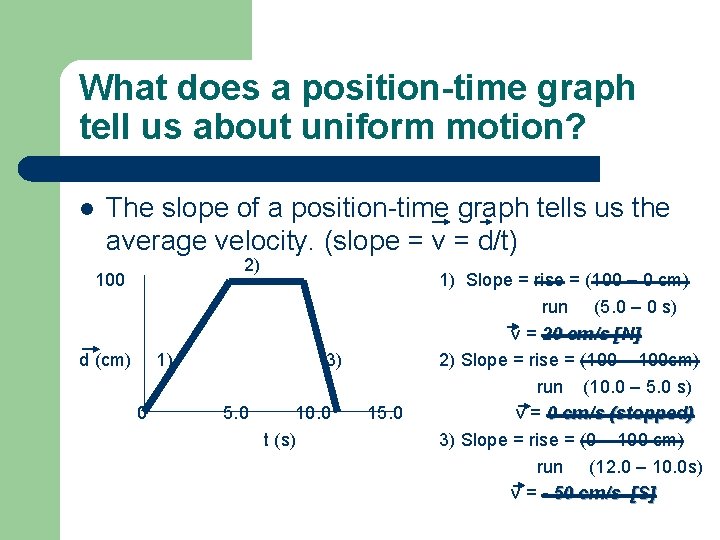
What does a position-time graph tell us about uniform motion? l The slope of a position-time graph tells us the average velocity. (slope = v = d/t) 2) 100 d (cm) 1) 0 3) 5. 0 10. 0 t (s) 15. 0 1) Slope = rise = (100 – 0 cm) run (5. 0 – 0 s) v = 20 cm/s [N] 2) Slope = rise = (100 – 100 cm) run (10. 0 – 5. 0 s) v = 0 cm/s (stopped) 3) Slope = rise = (0 – 100 cm) run (12. 0 – 10. 0 s) v = - 50 cm/s [S]

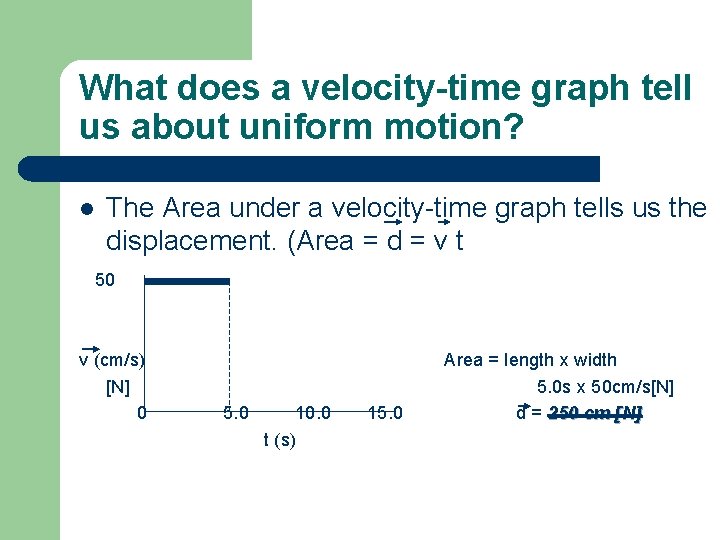
What does a velocity-time graph tell us about uniform motion? l The Area under a velocity-time graph tells us the displacement. (Area = d = v t 50 v (cm/s) [N] 0 5. 0 10. 0 t (s) 15. 0 Area = length x width 5. 0 s x 50 cm/s[N] d = 250 cm [N]

Try some on your own l Assignment book Questions

Different types of graphs

What is the formula for acceleration? Acceleration is the change in velocity over a specific time interval. l Acceleration(m/s/s) = change in velocity (m/s) change in time (s) l Accleration = (final velocity – initial velocity) change in time a = (vf – vi) (vf-vi) t vf = vi + at a t NOTE: Rest or stopped means v = 0 m/s , l

vf = vi + a t Acceleration vf =final velocity (m/s) [ ] vf = 0 if brake to a stop vi= initial velocity(m/s) [ ] Formula vi= 0 if starting at rest vf- vi a t

Calculating acceleration from a word problem-example 1 vi A car travelling 70 km/h [E] changes its vf velocity to 90 km/h [E] in 4. 5 s. What is the average acceleration? l – – Step 1: vf=90 km/h=25 m/s; vi=70 km/h=19. 44. . m/s; t=4. 5 s; a=(vf-vi) t Step 2: a = (25 m/s-19. 44…m/s) 4. 5 s Step 3: 1. 2 m/s/s Step 4: The average acceleration of the car is 1. 2 m/s/s [E]

Calculating acceleration from a word problem-example 2 A sprinter has vi an average acceleration of 3. 0 m/s 2 from rest to his maximum velocity of vf 11. 0 m/s. Calculate the time needed to reach the maximum velocity. How does increasing the acceleration give the sprinter better results? l – – Step 1: t = (vf -vi=o vi ) a; t = vf a Step 2: t =11. 0 m/s 3. 0 m/s 2 Step 3: t = 3. 7 s Step 4: It takes 3. 7 s for the sprinter to reach his maximum velocity.

Calculating acceleration from a word problem-example 3 l vi A group of teens riding a tube start from rest and accelerate at 1. 15 m/s 2. What is the speed after 6. 0 s? vf = ? – – Step 1: vf =vvi=o i + a t; vf = a t Step 2: vf =(1. 15 m/s 2)(6. 0 s) Step 3: vf = 6. 9 m/s Step 4: The teens reach a speed of 6. 9 m/s after traveling down the hill for 6. 0 s.

Try some on your own l Solve question 30, 33 & 34 from your assignment books on your own. Show your steps l Compare your answer with the people in the group - be ready to demonstrate your questions on the board for a penny!

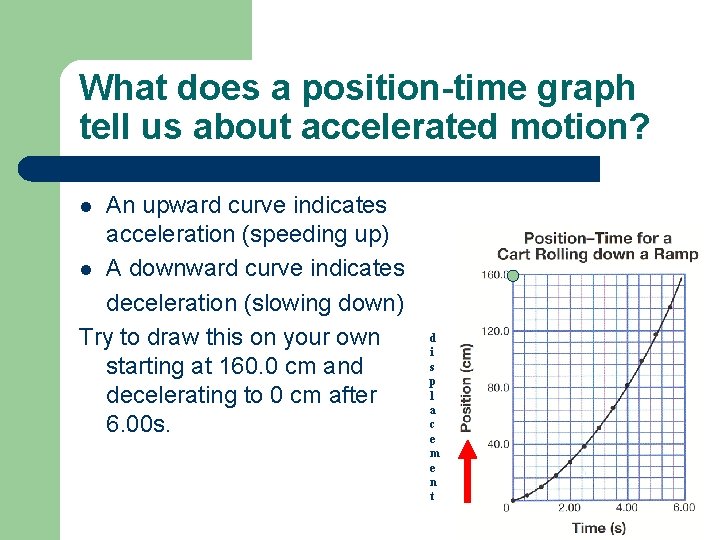
What does a position-time graph tell us about accelerated motion? An upward curve indicates acceleration (speeding up) l A downward curve indicates deceleration (slowing down) Try to draw this on your own starting at 160. 0 cm and decelerating to 0 cm after 6. 00 s. l d i s p l a c e m e n t

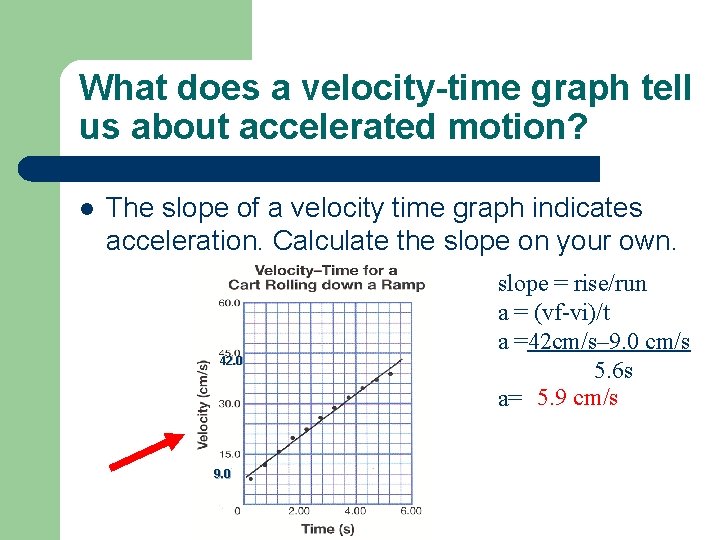
What does a velocity-time graph tell us about accelerated motion? l The slope of a velocity time graph indicates acceleration. Calculate the slope on your own. 42. 0 9. 0 slope = rise/run a = (vf-vi)/t a =42 cm/s– 9. 0 cm/s 5. 6 s a= 5. 9 cm/s

Determining negative acceleration. l Objects that fall accelerate at -9. 81 m/s/s due to gravity (g). These objects have a negative acceleration because they are heading in a negative direction. Add this to your databooks. g = 9. 81 m/s/s (down)

Try some on your own l l On your own do Questions 20, 26, 27 & 28 in your assignment book. Show your steps. Groups - be ready to demonstrate your questions on the board for a penny.

2. What is the equation for acceleration? 3. A car travelling 70 km/h [E] changes its velocity to 90 km/h [E] in 4. 5 s. What is the average acceleration? 4. Use the velocity/time graph to find acceleration. Velocity (m/s) 1. What is acceleration? 1 2 3 4 5 6 7 8 9 10 SEE WHAT YOU KNOW 0 1 2 3 4 5 6 7 8 9 10 Time (s) 5. What is the value of acceleration due to gravity?

SEE WHAT YOU KNOW 1. What is acceleration? change in velocity over a specific time interval. 2. What is the equation for acceleration? a = (vf-vi)/∆t 3. A car travelling 70 km/h [E] changes its velocity to 90 km/h [E] in 4. 5 s. What is the average acceleration? Step 1: vf=90 km/h=25 m/s; vi=70 km/h=19. 44. . m/s; t=4. 5 s; a=(vf-vi) t Step 2: a = (25 m/s-19. 44…m/s) 4. 5 s Step 3: 1. 2 m/s/s Step 4: The average acceleration of the car is 1. 2 m/s/s [E]

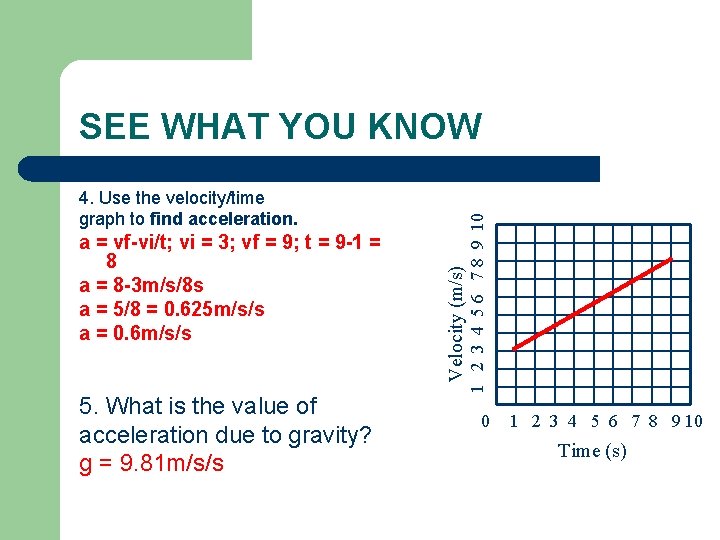
a = vf-vi/t; vi = 3; vf = 9; t = 9 -1 = 8 a = 8 -3 m/s/8 s a = 5/8 = 0. 625 m/s/s a = 0. 6 m/s/s 5. What is the value of acceleration due to gravity? g = 9. 81 m/s/s Velocity (m/s) 4. Use the velocity/time graph to find acceleration. 1 2 3 4 5 6 7 8 9 10 SEE WHAT YOU KNOW 0 1 2 3 4 5 6 7 8 9 10 Time (s)

Lesson 1. 6: Calculating Displacement during acceleration

Determining the minimum length (displacement) of an acceleration lane Displacement = area under a speed-time graph l Displacement(m[ ])=average velocity(m/s)xtime(s) l d = (vf+vi) x t; Don’t need acceleration. 2 d Formula in t = ___d____ (vf+vi) t databook (vf + vi)/2 2 l

Formula 9 in databook No a

Example problem using the displacement equation l l A car enters the acceleration lane with an initial velocity of 20. 0 km/h [E]. The car reaches a final velocity of 100. 0 km/h [E] in 8. 00 s. What is the displacement in meters? SOLUTION: – – l Step 1: vi=20. 0 km/hx 1000/3600=5. 55…m/s[E]; vf=100 km/hx 1000/3600=27. 77…m/s[E]; t=8. 00 s; d= t(vf+vi)2 Step 2: d=8. 00 s(27. 77…+5. 55…m/s[E])/2 Step 3: d=133 m [E] Step 4: The displacement is 133 m [E] Try practice question 32 on page 208

Displacement example using acceleration due to gravity l l l Gravity causes objects to accelerate at -9. 81 m/s/s (down) =g or decelerate at 9. 81 m/s/s (up) up Using acceleration due to gravity and the acceleration formula, what is the initial velocity of the baseball if it traveled for 1. 8 s to it’s maximum height where it briefly stops. SOLUTION: – – Step 1: Step 2: Step 3: Step 4: vi = vf-at; vf = 0 m/s (up), a = -9. 81 m/s/s (up), ∆t = 1. 8 s vi = 0 m/s - 9. 81 m/s/s (up) * 1. 8 s vi = 17. 658 m/s vi = 18 m/s

Try Some On Your Own l l Choose a partner (get into pairs) One partner solve #32 from your Assignment Book 2 nd partner solve #33 from your Assignment Book Once solved, teach your partner how you solved the question - Each person needs to write their partner’s question/answer down as they are being taught.

Another displacement equation l l l Displacement = area under the graph Displacement = rectangle area + triangle area Displacement = lw + ½ bh Displacement = initial velocity x time + 0. 5 acceleration x time d=(vi t) + (0. 5 a t 2) - no final velocity (vf) formula #8 in databook

Another Displacement Equation No vf

Draw and arrow from this slide to “another displacement equation” slide. It is out of order in your notes. Finding displacement when passing another vehicle on the highway. l l A care travelling 90 km/h [E] accelerates at 0. 50 m/s 2 while passing another vehicle. It it takes 5. 0 s to pass, what is the displacement? SOLUTION – – Step 1: Step 2: Step 3: Step 4: vi = 90 km/h /3. 6 = 25 m/s (E), a= 0. 50 m/s 2 (E), t=5. 0 s d = (vit) + (0. 5 at 2); d = (25 x 5) + (0. 5 x 0. 50 x 52); 125 + 6. 25 d = 131. 25 = 1. 3 x 102 m (E) Try practice problem 33 on page 209

Example 1 with the new displacement equation l l Juanita leaves the trampoline with an initial velocity of 11. 8 m/s up. Determine the displacement after 0. 80 s. SOLUTION: – – Step 1: Step 2: Step 3: Step 4: vi = 11. 8 m/s (up), a = 9. 81 m/s 2, t =0. 80 s d= (vit) + (0. 5 at 2) d = (11. 8 x 0. 8) + (0. 5 x-9. 81 x 0. 82) d= 9. 44 + -3. 1392 = 6. 3 m (up)

You Create It! l Each person has 3 min. to create a word problem that solves for displacement. – – l l l Choose which displacement equation you want to use Write the question and write the solution on the back Have one other person in your group check your question and answer (make any adjustments) Send questions to another group Solve a question!!

Example 2 using the new displacement equation (WATER) l l A diver steps off the edge of a platform and enters the water 5. 0 m below. If the initial velocity of the diver was zero, determine the time it takes the diver to reach the water. SOLUTION: – – Step 1: Step 2: Step 3: Step 4: d = 5. 0 m, vi = 0, a = +9. 81 m/s 2 d = vit + 0. 5 at 2 5. 0/(0. 5 x 9. 81) = 0 + 0. 5 x 9. 81 x t 2/(0. 5 x 9. 81) 1. 0193…. = t 2; t= 1. 0 s Try questions 34 – 35 on page 211

Lesson 1. 7 & 1. 8: Stopping distance and braking

What is reaction distance and braking distance? Reaction distance: the distance a vehicle travels while the driver is reacting. d=v t l Braking distance: the distance a vehicle travels from the moment the brakes are first applied to the time the vehicle stops. t = vi/a; d= t(vi/2) l Stopping distance = reaction distance + braking distance Try question 36 l

Your Reaction Time! WHAT TO RECORD: l The time (t) it took to catch the meter stick s l The measurement of where you caught the meter stick (dr) m l Record answer

dr = Reaction Distance b ds = dr + d b dr = v*t db = Braking Distance ds = Stopping Distance

Example of calculating stopping distance l l If a driver is traveling at 30. 6 m/s, reacts after 1. 50 s & decelerates at 5. 85 m/s/s, what is the stopping distance? SOLUTION: – Reaction distance: l l – Braking distance: t = 5. 23 s l l – Step 1: dr = v*t Step 2: dr = 30. 6 m/s*1. 50 s Step 3: dr = 45. 9 m Step 4: dr = 45. 9 m Step 1: db = (vi/2)t Step 2: db = (30. 6 m/s/2)5. 23 s Step 3: db = (15. 3 m/s)*5. 23 s Step 4: db = 80. 0 m Stopping distance: ds = dr + db 45. 9+80. 0 = 125. 9 m Try Practice Question 38 on page 216

Controlling traffic at intersections l A vehicle travelling at 60. 0 km/h approaches an intersection where the light has just turned yellow. a) If the reaction time is 1. 50 s and deceleration is 5. 85 m/s/s, what is the stopping distance? (db-time = 2. 85 s) Step 1: dr = v*t Step 2: (60. 0 km/h)/3. 6 = 16. 7 m/s * 1. 50 s = 25. 1 m Step 3: (t = 2. 85 s) db = (vi/2)t = (16. 7 m/s /2)2. 85 s = 23. 8 m Step 4: ds = dr+ db 25. 1 m + 23. 8 = 48. 9 m

Controlling traffic at intersections (OPTIONAL) l A vehicle travelling at 60. 0 km/h approaches an intersection where the light has just turned yellow. b) Using your answer in part a) & the info above, what is the time required for the driver to travel this distance (area of no return) at a uniform speed. Step 1: total time = tr(reaction time) + tb(braking time) Step 2: total time = 1. 50 s + 2. 85 s Step 3: total time = 4. 35 s Step 4: The time required is 4. 35 s c) How long should the light remain yellow? The light should remain yellow longer than 4. 35 s. Try Question 39 -42 on page 218

SEE WHAT YOU KNOW l l If a driver is traveling at 30. 6 m/s, reacts after 1. 50 s & decelerates at 5. 85 m/s/s, what is the stopping distance? SOLUTION: – Reaction distance: l l – Braking distance: t = 5. 23 s l l – – Step 1: dr = v*t Step 2: dr = 30. 6 m/s*1. 50 s Step 3: dr = 45. 9 m Step 4: dr = 45. 9 m Step 1: db = (vi/2)t Step 2: db = (30. 6 m/s/2)5. 23 s Step 3: db = (15. 3 m/s)*5. 23 s Step 4: db = 80. 0 m Stopping distance: ds = dr + db 45. 9+80. 0 = 125. 9 m

Lesson 1. 9: Newton’s First & Second Laws of Motion

What are factors affecting deceleration? l Forces of friction: Force of air resistance 2. Force of road resistance (Ice or wet conditions should be considered since they decrease this force 3. Force applied by the braking system NET FORCE: sum of all these forces 1. Mass: The larger the mass, the longer it takes to decelerate. Try question 43 -44 on page 222 l

Newton’s Laws l l There are 3 laws of motion We will begin looking at them in this order for understandings sake: l l l Newton’s 2 nd Law Newton’s 1 st Law Newton’s 3 rd Law

What is Newton’s Second law l l An object will accelerate in the direction of the net force Formula: a = F or Fnet = ma m

In Your Databooks… Units for Force are kg*m/s/s or N [] 2 nd Law F m [] a

Example of Newton’s Second law l A vehicle with a mass of 1250 kg is travelling 45 km/h east, when the driver brakes and stops. a) Determine acceleration if the force is 7000 N. – – l Step 1: Step 2: Step 3: Step 4: b) Determine the length of time the net force must be applied to stop (using your acceleration formula) – – Step 1: t = (vf-vi)/a Step 2: Step 3: Step 4: Try questions 45 -46 on page 226.

What is Newton’s 1 st Law of Motion l l In the absence of a net force, an object in motion will tend to maintain its velocity and an object at rest will tend to remain at rest. Net Force can be calculated by adding the applied force and the frictional forces. – – Forces in a West and South direction are negative. Forces in a North and East direction are positive. [] [] []

Appling Newton’s first law l a) Determine the net force & acceleration of: A motorcycle with a mass of 245 kg, applies a force of 1880 N [W] to over come frictional forces of 520 N [E]. Step 1: Step 2: Step 3: Step 4: b) A car with a mass of 1075 kg, applies a force of 4800 N [W] to overcome frictional forces of 4800 N [E] Step 1: Step 2: Step 3: Step 4: Which Example Illustrates Isaac Newton’s 1 st Law?

What is inertia? l l Inertia is the property of an object to resist changes in its state of motion. Try practice questions 47 -49 on page 233. Which object from the slide before (245 kg or 1075 kg) has the most inertia? 1075 kg has more inertia than the 245 kg object because it resists changes more.

Seatbelts – Why do they work? l l l Discuss in your groups the usefulness of a seatbelt using Newton’s 1 st Law and Inertia. Pick a spokes person to share with the class your answer. Watch This…

Lesson 2. 4: A closer look at forces and Newton’s Third Law

Newton’s 3 rd Law l l Whenever on object exerts a force on a second object, the second object exerts an equal but opposite force on the first object. F 1 on 2 = -F 2 on 1

Other examples of the 3 rd Law A car is cruising down the street. A rocket is lifting off toward space. A ball is dropped off a very tall building. The car’s tires push down on the road. The rocket pushes down on the gas (rocket fuel exhaust). The Earth is pulling the ball down. The road is pushing up on the car’s tires. The gas pushes up on the rocket. The ball is pulling up the Earth!

Example Problems Identify the action and reaction forces in the illustrations handed out to you. l l Illustrations will be handed out for you to label the forces.

SEE WHAT YOU KNOW • An object will accelerate in the direction of the net force • Fnet = Fa + Ff • F 1 on 2 = -F 2 on 1 • Whenever one object exerts a force on a second object, the second object exerts an equal but opposite force on the first object. • Fnet = ma • In the absence of a net force, an object in motion will tend to maintain its velocity and an object at rest will tend to remain at rest.

Newton’s 2 nd Law Newton’s 1 st Law Newton’s 3 rd Law An object will accelerate in the direction of the net force In the absence of a net force, an object in motion will tend to maintain its velocity and an object at rest will tend to remain at rest. Whenever one object exerts a force on a second object, the second object exerts an equal but opposite force on the first object. Fnet = ma Fnet = Fa = Ff F 1 on 2 = -F 2 on 1 Which of Newton’s Laws is demonstrated in the word problem below? (Place a check mark under the correct heading) a)A vehicle with a mass of 1250 kg is accelerating at 5. 6 m/s/s East. Determine, just the force of the vehicle. Step 1: Fnet = ma, m = 1250 kg, a = 5. 6 m/s/s Step 2: Fnet = 1250 kg*5. 6 m/s/s [E] Step 3: Fnet = 7000 N [E] Step 4: Fnet = 7. 0 X 103 N [E]

Chapter 2: Collisions 2. 1 Momentum 2. 2 Change in momentum

Lesson 2. 1: Momentum

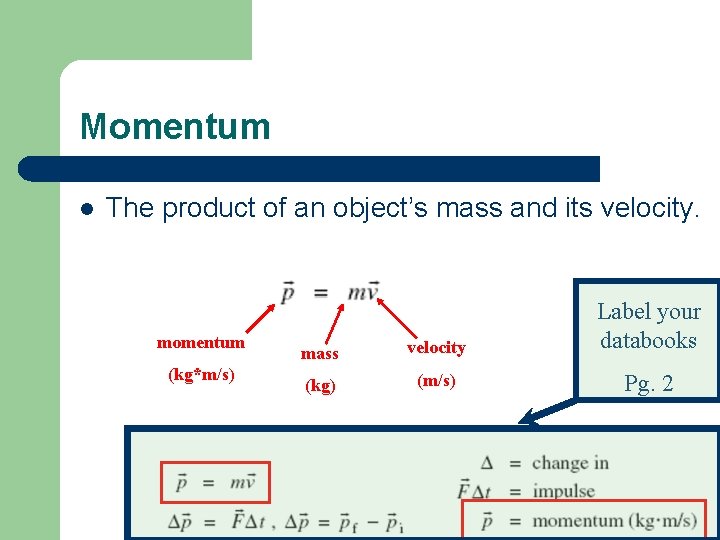
Momentum l The product of an object’s mass and its velocity. momentum (kg*m/s) mass velocity Label your databooks (kg) (m/s) Pg. 2

Example Problem 2. 1 Determine the momentum of a vehicle with a mass of 2100 kg moving at a velocity of 22 m/s[E].

Example Problem 2. 1 Determine the momentum of a vehicle with a mass of 2100 kg moving at a velocity of 22 m/s [E]. (Let east be the positive direction) SOLUTION Step 1: p = mv, m = 2100 kg, v = +22 m/s [E], p = ? Step 2: p = mv; p = (2100 kg) (+22 m/s) p = + 4. 6 X 104 kg*m/s [E]

Now You Try l Can these objects have the same momentum, ? l m = 0. 43 kg, m = 0. 17 kg, m= 0. 058 kg If the velocity is the same, which object has the most momentum? If the momentum is the same, which object will have the highest speed? l l

More practice l l l Do # 1 -5 of the Chapter 2 questions in your Assignment Book Q 1) Q 2) Q 3) Q 4) Q 5)

See What You Know 1. Momentum is the product of an object’s ______ and it’s _____. 2. Write the formula for finding momentum. 3. Fill in the units for each value: m = _____, v = _____, p = _____ 4. Determine the momentum of a vehicle with a mass of 2020 kg moving at a velocity of 24 m/s[E]. 5. Which object will have the larger momentum if moving at the same velocity? A bowling ball or a soccer ball?

See What You Know 1. Momentum is the product of an object’s mass and it’s velocity. 2. Write the formula for finding momentum. p = mv 3. Fill in the units for each value: m = kg, v = m/s, p = kg*m/s 4. Determine the momentum of a vehicle with a mass of 2020 kg moving at a velocity of 24 m/s[E]. 4. 8 E 4 5. Which object will have the larger momentum if moving at the same velocity? A bowling ball or a soccer ball?

Lesson 2. 2: Change in Momentum

Momentum Changes l l l Momentum of an owl changes when it interacts with it’s prey because the velocity changes. Momentum of a snow ball changes when a person rolls it across a field because the mass changes. Equation for momentum is p = mv, so a change in momentum is caused by change in mass(m) or velocity(v). (we will focus on change in velocity for the rest of class) What variable in the formula changes for the owl? velocity

Change in Momentum A change in momentum is equal to the mass times the change in velocity. Formula: ∆p = m(vf-vi)

Example Problem (add this to your notes) A 4. 00 kg water balloon reaches a velocity of 31. 3 m/s just before striking the ground. The velocity of the balloon is 0 m/s after striking the ground. Calculate the change in momentum. Answer: Step 1 ∆p = m(vf-vi) Step 2 ∆p = 4. 00 kg(0 m/s – 31. 3 m/s) Step 3 ∆p = 4. 00 kg(-31. 3 m/s) Step 4 ∆p =-125. 2 kg*m/s= -1. 25 X 102 kg*m/s

Force formulas that cause Change in Momentum 1. FIRST FORCE FORMULA: • a = vf-vi and F =m (vf-vi) a ∆t ∆t Force is equal to the mass times change in velocity, divided by time. 2. SECOND FORCE FORMULA ∆p = m (vf-vi) and F= m(v ∆pf-vi) ∆t Force is equal to the change in momentum divided by time.

Force formulas that cause Change in Momentum in your databooklets F = Force (N) m = mass (kg) This formula Rearranged is: F= ∆p ∆t Copy this formula in your databook, next to the force formula. vf = final velocity (m/s) vi = initial velocity (m/s) t = time (s) p = momentum (kg*m/s)

Data Tool Kit m= vf = vi = t= NOTE: your direction will be [W]

Calculations 1 st Force Formula: F = m(vf-vi)/t Your Momentum: ∆p = m(vf-vi) 2 nd Force Formula: F = ∆p/t Your Momentum by manipulating the 2 nd Force Formula:

Example Problem #1 (2. 4 in the text) A 2. 1 kg barn owl flying at a velocity of 15 m/s[E] strikes head-on with the windshield of a car travelling 30 m/s[W]. If the time interval for the impact was 6. 7 X 10 -3 s, determine the force that acted on the owl. ANSWER: Step 1 F = m(vf-vi), m=2. 1 kg, vf=-30 m/s, vi=15 m/s, ∆t Step 2 F = 2. 1 kg(-30 m/s – 15 m/s) = 2. 1 kg(-45 m/s) 6. 7 X 10 -3 s Step 3 F = -1. 4 X 104 kg*m/s 2 Step 4 F = -1. 4 X 104 N OR 1. 4 X 104 N[W] 6. 7 X 10 -3 s

Example problem #2 A 2000 kg car travelling at 25 m/s [E] strikes a tree and comes to rest a) Calculate the change in momentum. b) If the impact took 0. 23 s, determine the force exerted on the car using the momentum from a). Answer: a) ∆p = m(vf-vi) = 2000 kg(0 m/s-25 m/s) = -50 X 103 N [E] b) F = ∆p = -50 X 103 N = -217391 N = 2. 2 X 105 N [E] ∆t 0. 23 s

Try some on your own A 500 g ball thrown at a velocity of 5. 00 m/s strikes a wall. After 0. 25 s, the ball rebounds back with a velocity of 4. 50 m/s. a) What is the change in momentum? b) What is the force exerted on the ball using F = m(vf-vi)/t ? c) What is the force exerted on the ball using F = ∆p/t ? 1.

Answers to Try It On Your Own a) What is the change in momentum? m=(Convert 500 g/1000) = 0. 5 kg, vf = 4. 50 m/s, vi= 5. 00 m/s ∆p=m(vf-vi)/∆t = 0. 5 kg(4. 50 m/s-5. 00 m/s) ∆p=-0. 25 kg*m/s OR -0. 25 N b) What is the force exerted on the ball using F = m(vf-vi)/t ? F = 0. 5 kg(4. 50 m/s-5. 00 m/s)/0. 25 s F = -0. 25 kg*m/s / 0. 25 s = -1. 0 kg*m/s/s or -1. 0 N c) What is the force exerted on the ball using F = ∆p/t ? F = ∆p/∆t F = -0. 25 kg*m/s / 0. 25 s = -1. 0 kg*m/s/s or -1. 0 N

Factors Affecting Change in Momentum Change in momentum depends on the force applied to the object and the time interval over which the force acts. Formula: momentum can be determined from the force formula manipulated ∆p F ∆t Highlight the formula in your databook and add the triangle.

Example Problem 2. 5 Calculate the ∆p for: Case 1: Two dogs pull a sled, each with a force of 15 N and a total force of 30 N. If they pull for 10 s, what is their change in momentum? ∆p = F∆t ∆p = 30 N*10 s= 3. 0 E 2 kg*m/s Case 2: Four dogs pull a sled, each with a force of 15 N and a total force of 60 N if they pull for 10 s, what is their change in momentum? ∆p = F∆t ∆p = 60 N * 10 s= 6. 0 E 2 kg*m/s Case 3: Two dogs pull a sled, each with a force of 15 N and a total force of 30 N. If they pull for 5 s, what is their change in momentum? ∆p = F∆t ∆p = 30 N * 5 s = 1. 5 E 2 kg*m/s Case 4: Four dogs pull a sled, each with a force of 7. 5 N and a total force of 30 N if they pull for 10 s, what is their change in momentum? ∆p = F∆t ∆p = 30 N * 10 s= 3. 0 E 2 kg*m/s

Case Study Questions 1. 2. 3. 4. Which dog sled had the most momentum and why? Which dog sled had the least momentum and why? Why did case 1 and 4 have the same momentum, even though they had a different number of dogs? What two factors affect momentum?

Try it on your own l Try practice questions #6, 8 and 9 from your assignment books. l If you need more practice Try practice questions #7, 8 on pg. 251

See What You Know 1. Name two factors that affect a change in momentum? 2. A 2. 1 kg barn owl flying at a velocity of 15 m/s[E] strikes head-on with the windshield of a car travelling 30 m/s[W]. If the time interval for the impact was 6. 7 X 10 -3 s, determine the force that acted on the owl. 3. What is the 2 nd Force Formula? 4. Four dogs pull a sled, each with a force of 15 N and a total force of 60 N if they pull for 10 s, what is their change in momentum? 5. Is momentum a scalar or a vector quantity?

See What You Know 1. Name two factors that can affect a change in momentum? a change in mass and a change in velocity OR force and a change in time 2. A 2. 1 kg barn owl flying at a velocity of 15 m/s[E] strikes head-on with the windshield of a car travelling 30 m/s[W]. If the time interval for the impact was 6. 7 X 10 -3 s, determine the force that acted on the owl. Step 1 F = m(vf-vi), m=2. 1 kg, vf=-30 m/s, vi=15 m/s, ∆t Step 2 F = 2. 1 kg(-30 m/s – 15 m/s) = 2. 1 kg(-45 m/s) 6. 7 X 10 -3 s Step 3 F = -1. 4 X 104 kg*m/s 2 Step 4 F = -1. 4 X 104 N OR 1. 4 X 104 N[W]

See What You Know 3. What is the 2 nd Force Formula? F = ∆p ∆t 4. Four dogs pull a sled, each with a force of 15 N and a total force of 60 N if they pull for 10 s, what is their change in momentum? ∆p = F∆t ∆p = 60 N * 10 s= + 6. 0 E 2 kg*m/s 5. Is momentum a scalar or a vector quantity? quantity

Lesson 2. 3: Impulse

What is impulse? The product of the net force applied to an object and the time interval during which the force acts. l Is also equal to the change in momentum. l

What two factors influence impulse? l l l From the description of impulse, what do you think are the two factors that influence impulse? Force and Time Underline Force and Time in the description (located in the last slide)

What is the formula for impulse? Impulse does not have it’s own symbol, it is represented by the word impulse or the variables F∆t. impulse = F∆t

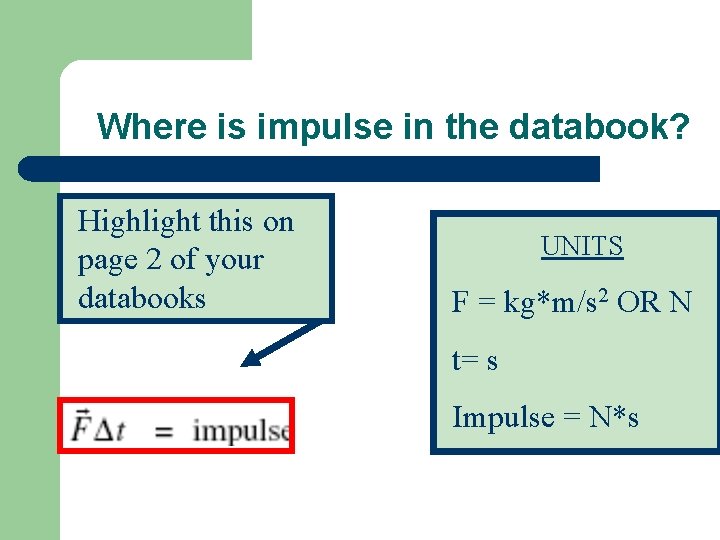
Where is impulse in the databook? Highlight this on page 2 of your databooks UNITS F = kg*m/s 2 OR N t= s Impulse = N*s

Example of solving a impulse problem? A hockey puck strikes a goalie’s mask. The time interval of the impact with the mask is 0. 012 s, during which the mask exerts a force of 400 N to change the momentum of the puck. Determine the impulse provided by the mask on the puck. impulse = F∆t impulse = + 400 N * 0. 012 s impulse = + 4. 8 N*s

Impulse and Destructive/Non. Destructive Force. l An impulse can keep destructive forces as small as possible by allowing for a long time interval for the interaction. impulse = F∆t On the other hand… l impulse = F∆t An impulse can increase destructive forces by allowing only a short time interval for the interaction.

What are ways that impulse affects our daily lives? Impulse affects. . . l How sports equipment is designed l The design of safety features in vehicles such as plastic shock absorbing bumpers, padded dashboards, shock-absorbing steering wheel, seat belts and air bags. l How we catch a baseball l How crash barriers are designed l How we remove snow from our boots l Etc.

Lesson 2. 5: Conservation of Momentum

Lesson 2. 6: Designing a helmet