Science 10 Aim Calculating Conversions Displacement Time speed

Science 10 �Aim: Calculating Conversions, Displacement, Time, speed and velocity

Agenda �Conversion examples �Conversion worksheet �Lunch – extra help time �Displacement and velocity notes �Homework: read p. 137 -154 (acceleration and velocity)) �Next class

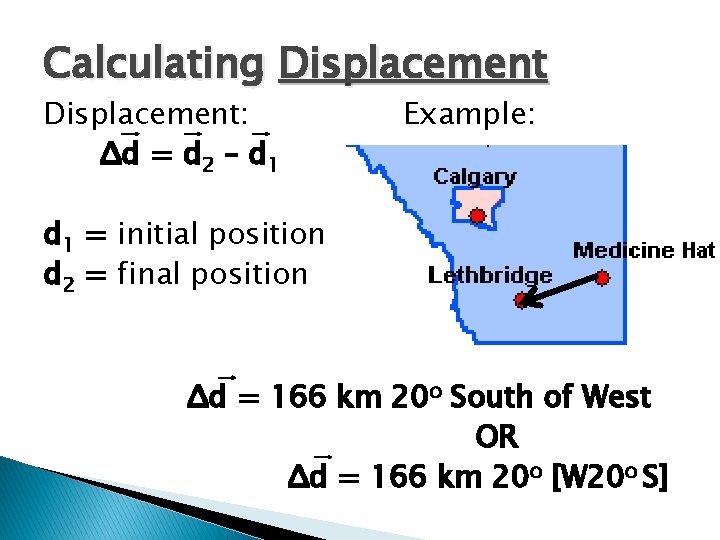
Calculating Displacement: Δd = d 2 – d 1 Example: d 1 = initial position d 2 = final position Δd = 166 km 20 o South of West OR Δd = 166 km 20 o [W 20 o S]

Calculating Total Distance Traveled Because distance is scalar (no direction), simply add together all the distance Example: A student ran 50 m east, 20 m south, 35 m west, and 25 m north. The total distance traveled is 230 m.

Vectors = magnitude and DIRECTION Therefore, to indicate direction in equations we use negative and positive numbers Direction conventions in Physics: Right is Positive (+) Left is Negative (-) East is Positive (+) West is Negative (-) North is Positive (+)South is Negative (-) Up is Positive (+) Down is Negative (-)

Calculating Total Displacement Total displacement of one object moving several different displacements is the vector sum of the displacements. Δdtotal = d 1 + d 2 + … Example: A student walks 23 m N, turns around and walks 33 m S. What is the student’s total displacement?

Calculating Total Displacement Total displacement of one object moving several different displacements is the vector sum of the displacements. Δdtotal = d 1 + d 2 + … Example: A student walks 23 m N, turns around and walks 33 m S. What is the student’s total displacement? Δdtotal = d 1 + d 2 + … = (+23 m) + (-33 m) = - 10 m (or 10 m S)

Time (t) is a point in time as it relates to your reference or zero time. A time interval ( t) is the difference between two times. t = t 2 – t 1

Speed (v) �A scalar �The distance traveled by an object during a given time interval divided by the time interval V avg = Δd = d 2 – d 1 Δt t 2 – t 1

Speed (v) �A scalar �The distance traveled by an object during a given time interval divided by the time interval V avg = Δd = d 2 – d 1 Δt t 2 – t 1 Example: A car travelled a distance of 550 m in a time interval of 35 s. What is its speed?

Velocity (v) �A vector �The displacement of an object during a time interval divided by the time interval V avg = Δd = d 2 – d 1 Δt t 2 – t 1

Velocity (v) Example: Two trainers with stopwatches are timing a runner who is training for a race. Both timers start their stopwatches when the runner leaves the starting point. The first trainer is standing at a position that is 12 m[S] of the starting point and the second trainer is 65 m[S] of the starting point. Each trainer stops her stopwatch when the runner passes her. The first trainer’s stopwatch reads 1. 6 s and the second trainer’s stopwatch reads 8. 7 s. What is the athlete’s velocity with running between the trainers?

Using Tables and Graphs. . . �Graphs are often used to represent the motion of an object. �Graphs are usually draw from the information contained in a data table �A table can be prepared by recording observations of a moving object

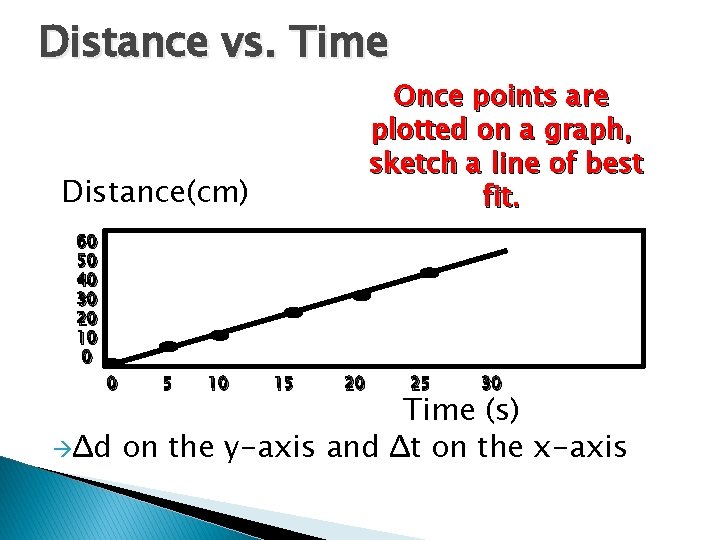
Distance vs. Time Once points are plotted on a graph, sketch a line of best fit. Distance(cm) 60 50 40 30 20 10 0 0 5 10 15 20 25 30 Time (s) Δd on the y-axis and Δt on the x-axis

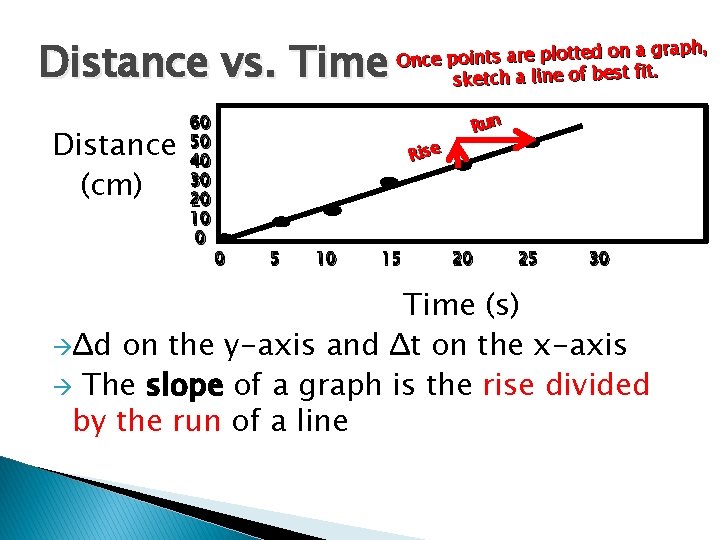
Distance vs. Time Distance (cm) 60 50 40 30 20 10 0 on a graph, Once points are plotted sketch a line of best fit. Rise 0 5 10 15 Run 20 25 30 Time (s) Δd on the y-axis and Δt on the x-axis The slope of a graph is the rise divided by the run of a line

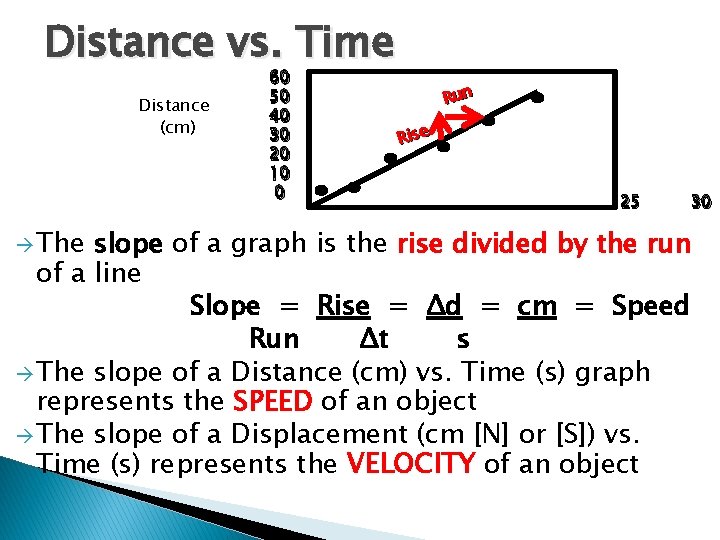
Distance vs. Time Distance (cm) The 60 50 40 30 20 10 0 Run Rise 0 5 10 15 20 25 slope of a graph is the rise divided by the run of a line Slope = Rise = Δd = cm = Speed Run Δt s The slope of a Distance (cm) vs. Time (s) graph represents the SPEED of an object The slope of a Displacement (cm [N] or [S]) vs. Time (s) represents the VELOCITY of an object 30

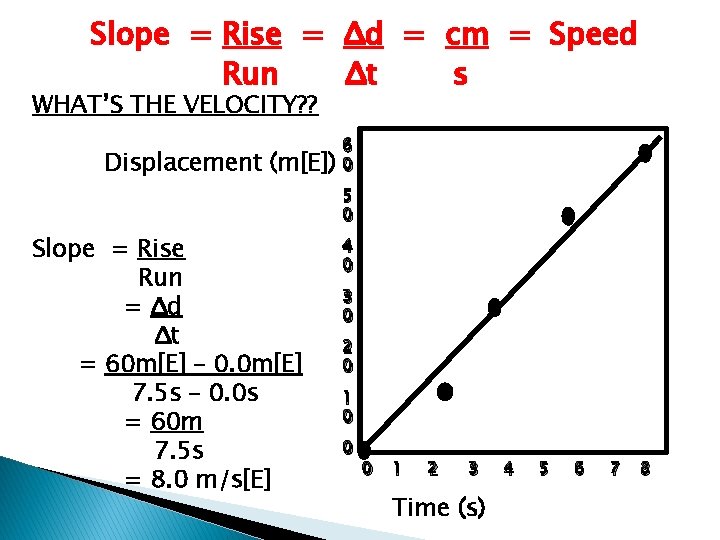
Slope = Rise = Δd = cm = Speed Run Δt s WHAT’S THE VELOCITY? ? Displacement (m[E]) 6 0 5 0 Slope = Rise Run = Δd Δt = 60 m[E] – 0. 0 m[E] 7. 5 s – 0. 0 s = 60 m 7. 5 s = 8. 0 m/s[E] 4 0 3 0 2 0 1 0 0 0 1 2 3 Time (s) 4 5 6 7 8

WHAT’S THE VELOCITY? ? 6 0 Displacement (m[E]) 5 0 4 0 3 0 2 0 1 0 0 0 1 2 3 4 5 Time (s) 6 7 8

Acceleration A Vector Quantity A measure of the change in velocity over a time of period Symbol = a Units = m/s 2

Two Ways to Accelerate an Object 1) 2) Change the speed of the object Change the direction of an object

Calculating Acceleration a = v 2 - v 1 t t 2 - t 1 When an object speeds up, it shows positive acceleration When an object slows down, it shows negative acceleration

Acceleration Question Example 1) A train starts at rest and reaches a speed of 54 km/h in 10 seconds. What is its acceleration?

Acceleration Question Example 2) An object starts from rest and accelerates for a time of 12 s. From 5. 0 to 8. 7 seconds, the car changes speed from 15 m/s to 27. 8 m/s. Calculate the acceleration of the object during this time period.

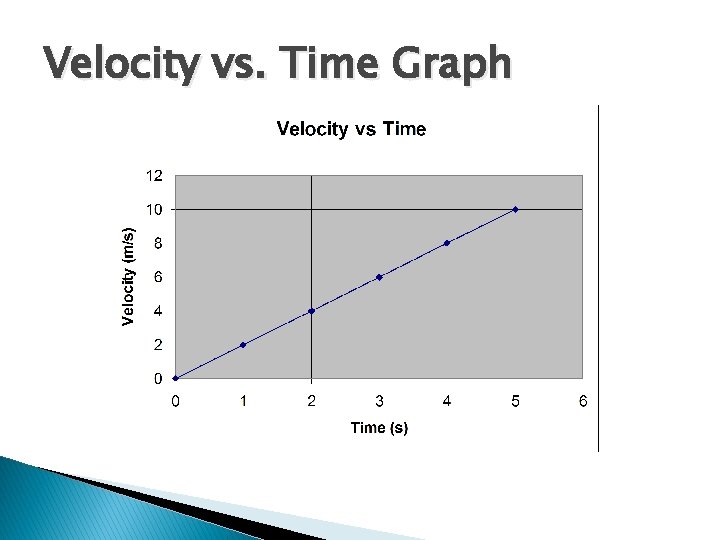
Velocity vs. Time Graph

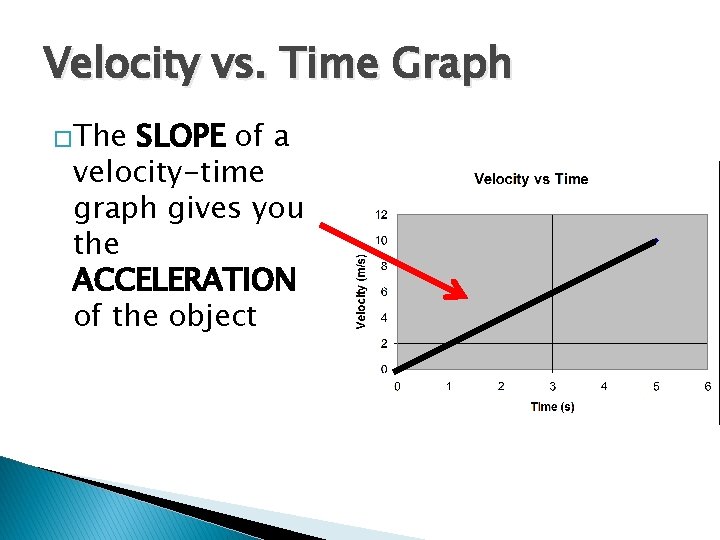
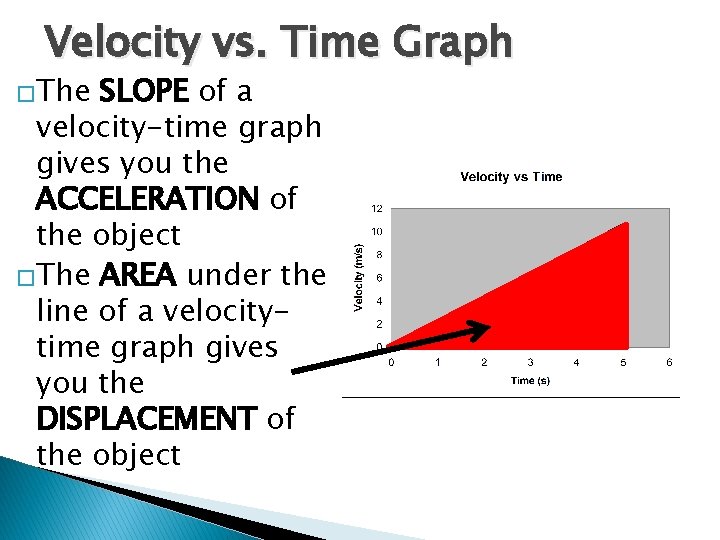
Velocity vs. Time Graph �The SLOPE of a velocity-time graph gives you the ACCELERATION of the object

Velocity vs. Time Graph �The SLOPE of a velocity-time graph gives you the ACCELERATION of the object �The AREA under the line of a velocitytime graph gives you the DISPLACEMENT of the object

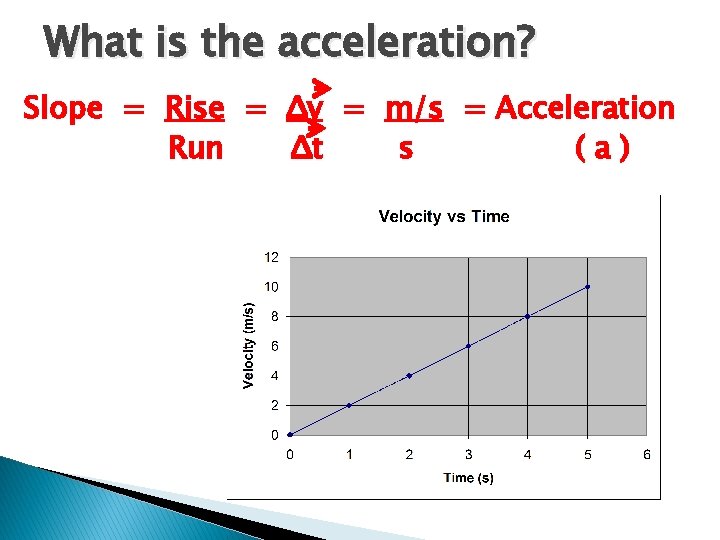
What is the acceleration? Slope = Rise = Δv = m/s = Acceleration Run Δt s (a)

WORK INDIVIDUALLY FIND THE ACCELERATION? 6 0 5 0 Velocity (m/s[N]) 4 0 3 0 2 0 1 0 0 0 1 2 3 4 5 Time (s) 6 7 8

Graphs and Motion

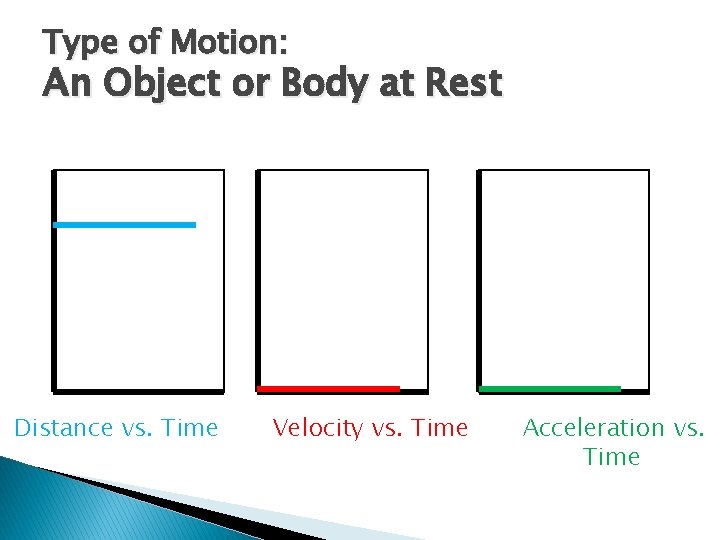
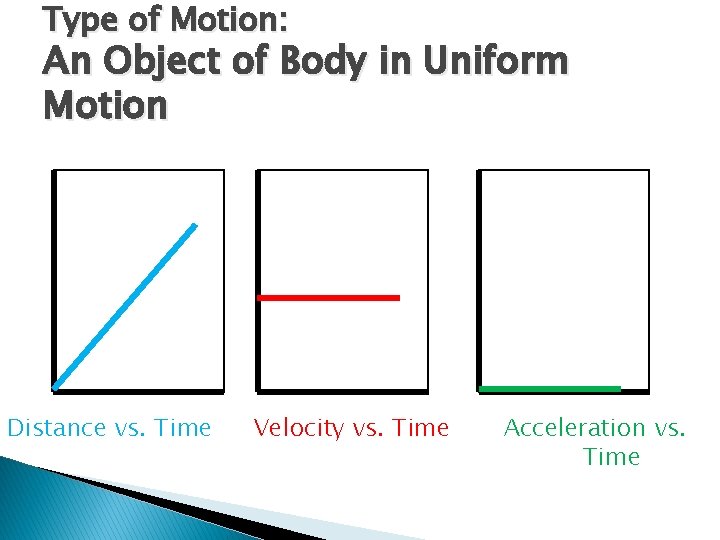
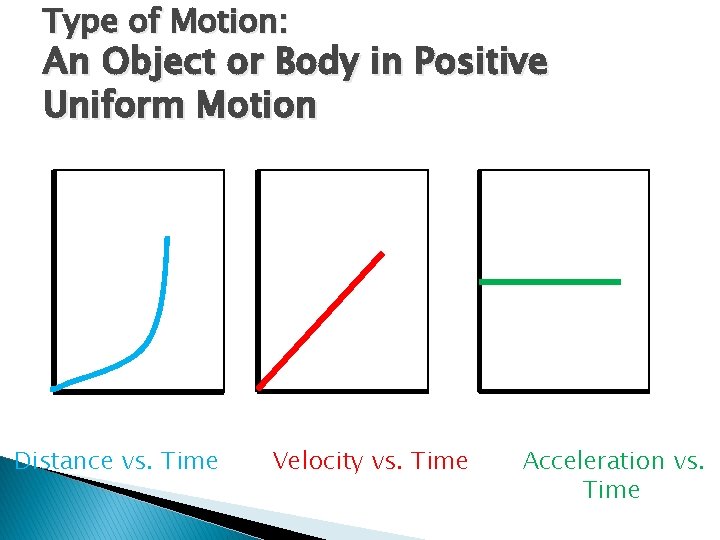
Graphs and Motion Graphs can be used to show different types of motion. 3 types of graphs that can show the same type of motion: Distance vs. Time Velocity vs. Time Acceleration vs. Time

Type of Motion: An Object or Body at Rest Distance vs. Time Velocity vs. Time Acceleration vs. Time

Type of Motion: An Object of Body in Uniform Motion Distance vs. Time Velocity vs. Time Acceleration vs. Time

Type of Motion: An Object or Body in Positive Uniform Motion Distance vs. Time Velocity vs. Time Acceleration vs. Time

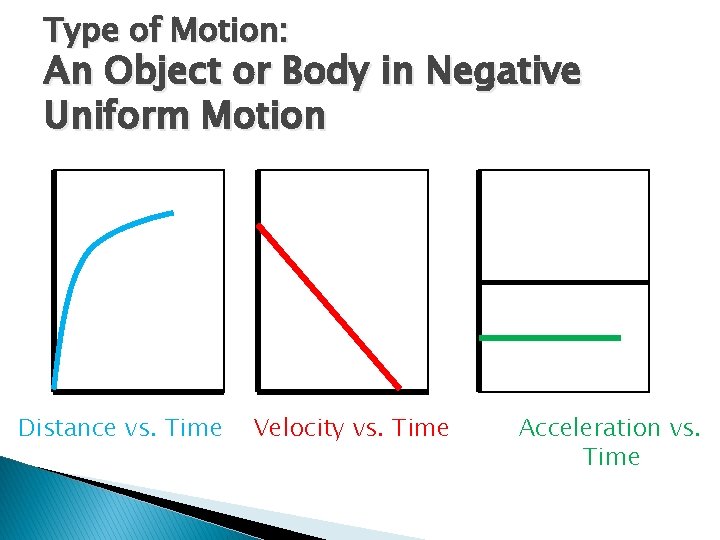
Type of Motion: An Object or Body in Negative Uniform Motion Distance vs. Time Velocity vs. Time Acceleration vs. Time