School of EECS Peking University Advanced Compiler Techniques

School of EECS, Peking University “Advanced Compiler Techniques” (Fall 2011) Loops Guo, Yao

Content n Concepts: Dominators n Depth-First Ordering n Back edges n Graph depth n Reducibility n Natural Loops n Efficiency of Iterative Algorithms n Fall 2011 “Advanced Compiler Techniques” 2

Loops are Important! n Loops dominate program execution time n n Needs special treatment during optimization Loops also affect the running time of program analyses n Fall 2011 e. g. , A dataflow problem can be solved in just a single pass if a program has no loops “Advanced Compiler Techniques” 3

Dominators n Node d dominates node n if every path from the entry to n goes through d. n n Quick observations: u u n written as: d dom n Every node dominates itself. The entry dominates every node. Common Cases: n n Fall 2011 The test of a while loop dominates all blocks in the loop body. The test of an if-then-else dominates all blocks in either branch. “Advanced Compiler Techniques” 4

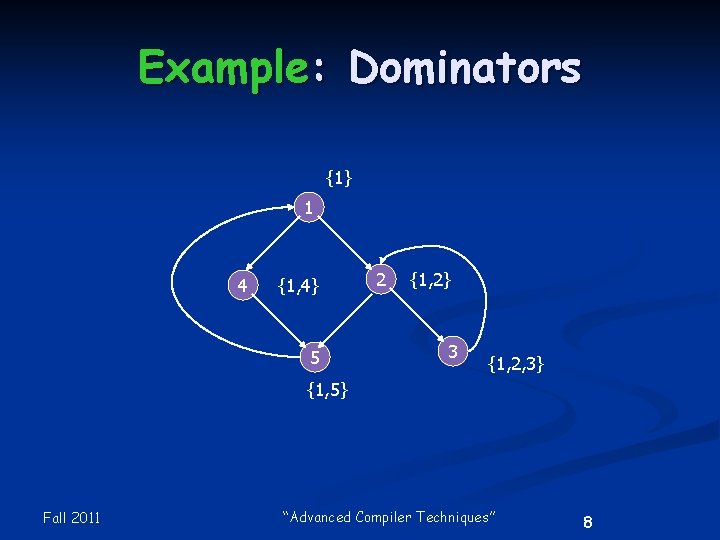
Example: Dominators 1 2 4 5 Fall 2011 3 “Advanced Compiler Techniques” 5

Dominator Tree n Immediate dominance: d idom n n n d dom n, d n, no m s. t. d dom m and m dom n Immediate dominance relationships form a tree 1 2 4 5 Fall 2011 1 2 4 3 “Advanced Compiler Techniques” 3 5 6

Finding Dominators n A dataflow analysis problem: For each node, find all of its dominators. Direction: forward n Confluence: set intersection n Boundary: OUT[Entry] = {Entry} n Initialization: OUT[B] = All nodes n Equations: n n OUT[B] = IN[B] U {B} n IN[B] = p is a predecessor of B OUT[p] Fall 2011 “Advanced Compiler Techniques” 7

Example: Dominators {1} 1 4 {1, 4} 5 2 {1, 2} 3 {1, 2, 3} {1, 5} Fall 2011 “Advanced Compiler Techniques” 8

Depth-First Search Start at entry. n If you can follow an edge to an unvisited node, do so. n If not, backtrack to your parent (node from which you were visited). n Fall 2011 “Advanced Compiler Techniques” 9

Depth-First Spanning Tree Root = entry. n Tree edges are the edges along which we first visit the node at the head. n 1 4 2 3 Fall 2011 5 “Advanced Compiler Techniques” 10

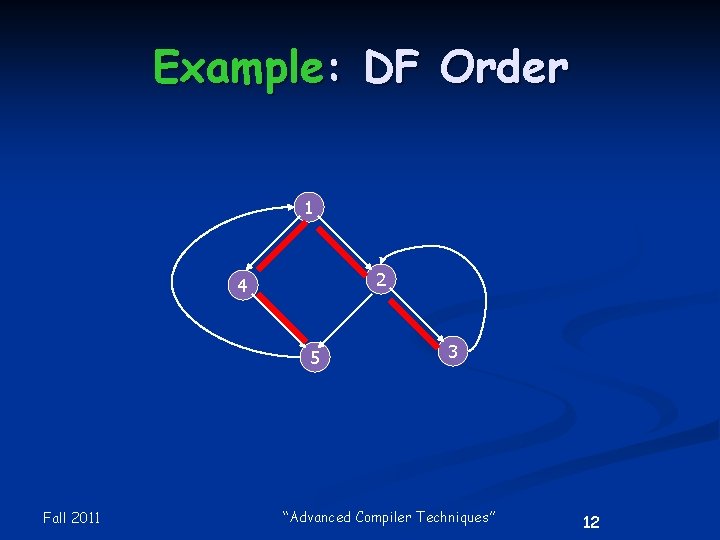
Depth-First Node Order The reverse of the order in which a DFS retreats from the nodes. n Alternatively, reverse of postorder traversal of the tree. n Fall 2011 “Advanced Compiler Techniques” 11

Example: DF Order 1 2 4 5 Fall 2011 3 “Advanced Compiler Techniques” 12

Four Kinds of Edges 1. 2. 3. 4. Tree edges. Advancing edges (node to proper descendant). Retreating edges (node to ancestor, including edges to self). Cross edges (between two nodes, neither of which is an ancestor of the other. Fall 2011 “Advanced Compiler Techniques” 13

A Little Magic n n Of these edges, only retreating edges go from high to low in DF order. Most surprising: all cross edges go right to left in the DFST. n Fall 2011 Assuming we add children of any node from the left. “Advanced Compiler Techniques” 14

Example: Non-Tree Edges Retreating Forward 1 2 4 3 5 Cross Fall 2011 “Advanced Compiler Techniques” 15

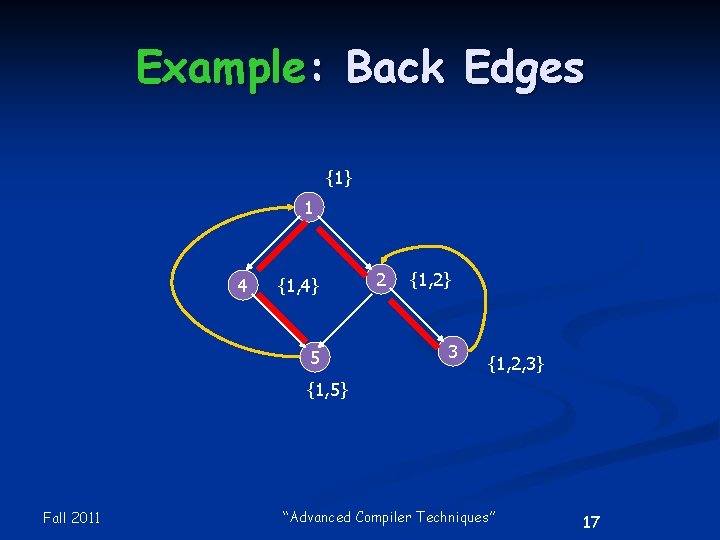
Back Edges An edge is a back edge if its head dominates its tail. n Theorem: Every back edge is a retreating edge in every DFST of every flow graph. n n Fall 2011 Converse almost always true, but not always. “Advanced Compiler Techniques” 16

Example: Back Edges {1} 1 4 {1, 4} 5 2 {1, 2} 3 {1, 2, 3} {1, 5} Fall 2011 “Advanced Compiler Techniques” 17

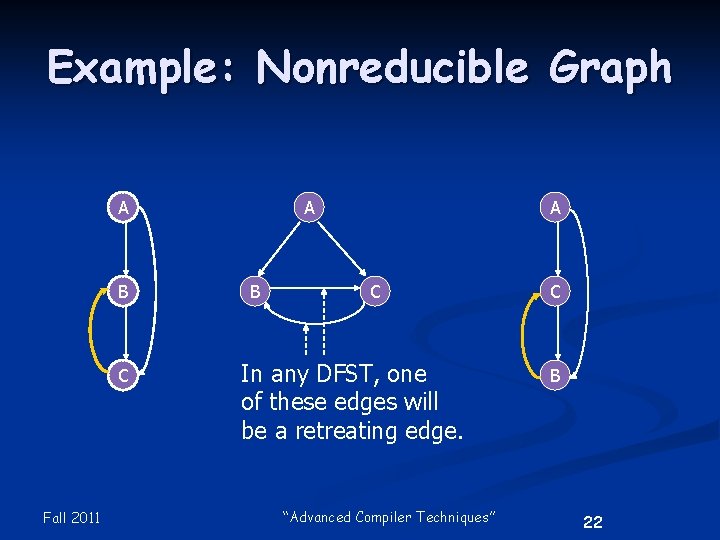
Reducible Flow Graphs n n A flow graph is reducible if every retreating edge in any DFST for that flow graph is a back edge. Testing reducibility: Take any DFST for the flow graph, remove the back edges, and check that the result is acyclic. Fall 2011 “Advanced Compiler Techniques” 18

Example: Remove Back Edges 1 2 4 5 Fall 2011 3 “Advanced Compiler Techniques” 19

Example: Remove Back Edges 1 2 4 5 3 Remaining graph is acyclic. Fall 2011 “Advanced Compiler Techniques” 20

Why Reducibility? n n Folk theorem: All flow graphs in practice are reducible. Fact: If you use only while-loops, forloops, repeat-loops, if-then(-else), break, and continue, then your flow graph is reducible. Fall 2011 “Advanced Compiler Techniques” 21

Example: Nonreducible Graph A B C Fall 2011 A B A C In any DFST, one of these edges will be a retreating edge. “Advanced Compiler Techniques” C B 22

Why Care About Back/Retreating Edges? 1. 2. Proper ordering of nodes during iterative algorithm assures number of passes limited by the number of “nested” back edges. Depth of nested loops upper-bounds the number of nested back edges. Fall 2011 “Advanced Compiler Techniques” 23

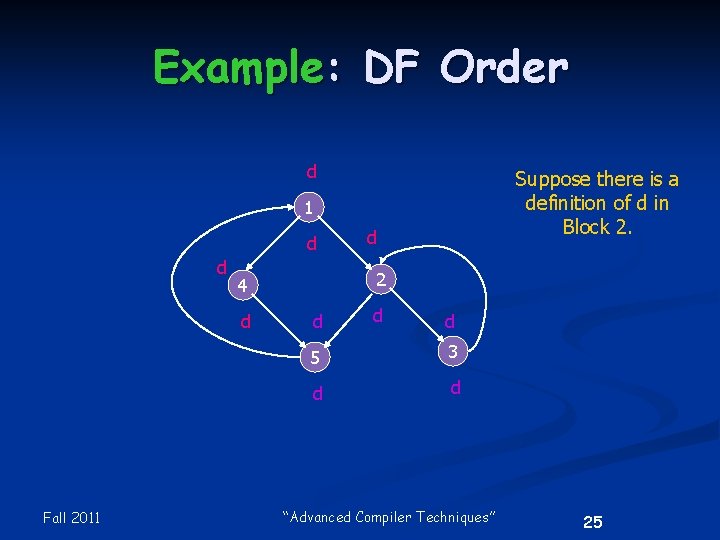
DF Order and Retreating Edges Suppose that for a Reaching Definitions analysis, we visit nodes during each iteration in DF order. n The fact that a definition d reaches a block will propagate in one pass along any increasing sequence of blocks. n When d arrives along a retreating edge, it is too late to propagate d from OUT to IN. n Fall 2011 “Advanced Compiler Techniques” 24

Example: DF Order d Suppose there is a definition of d in Block 2. 1 d d Fall 2011 2 4 d d d 5 3 d d “Advanced Compiler Techniques” 25

Depth of a Flow Graph The depth of a flow graph is the greatest number of retreating edges along any acyclic path. n For RD, if we use DF order to visit nodes, we converge in depth+2 passes. n Depth+1 passes to follow that number of increasing segments. n 1 more pass to realize we converged. n Fall 2011 “Advanced Compiler Techniques” 26

Example: Depth = 2 1 -> 4 ->7 - - -> 3 -> 10 ->17 - - -> retreating increasing Fall 2011 increasing 6 -> 18 -> 20 retreating increasing “Advanced Compiler Techniques” 27

Similarly. . . n AE also works in depth+2 passes. n n Unavailability propagates along retreatfree node sequences in one pass. So does LV if we use reverse of DF order. n Fall 2011 A use propagates backward along paths that do not use a retreating edge in one pass. “Advanced Compiler Techniques” 28

In General. . . n The depth+2 bound works for any monotone framework, as long as information only needs to propagate along acyclic paths. n Fall 2011 Example: if a definition reaches a point, it does so along an acyclic path. “Advanced Compiler Techniques” 29

However. . . n Constant propagation does not have this property. a=b L: a = b b = c c = 1 goto L Fall 2011 b=c c=1 “Advanced Compiler Techniques” 30

Why Depth+2 is Good n Normal control-flow constructs produce reducible flow graphs with the number of back edges at most the nesting depth of loops. n n Fall 2011 Nesting depth tends to be small. A study by Knuth has shown that average depth of typical flow graphs =~2. 75. “Advanced Compiler Techniques” 31

Example: Nested Loops 3 nested whileloops; depth = 3. Fall 2011 3 nested repeatloops; depth = 1 “Advanced Compiler Techniques” 32

Natural Loops n A natural loop is defined by: n A single entry-point called header na n header dominates all nodes in the loop A back edge that enters the loop header n Otherwise, it is not possible for the flow of control to return to the header directly from the "loop" ; i. e. , there really is no loop. Fall 2011 “Advanced Compiler Techniques” 33

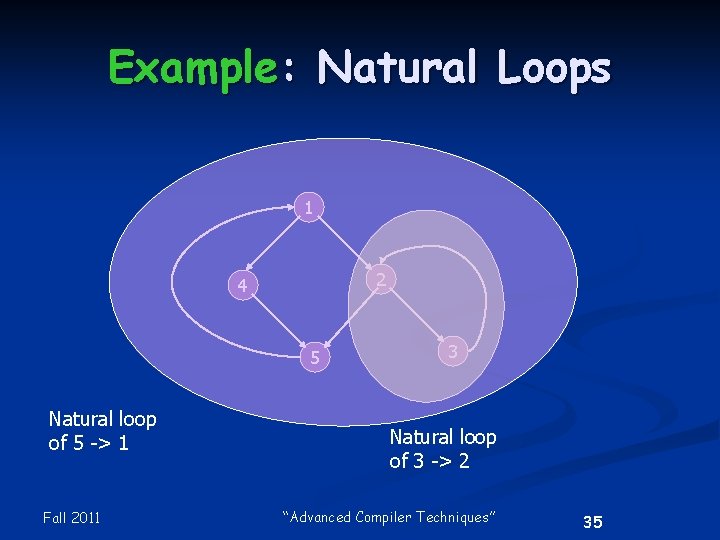
Find Natural Loops n n n The natural loop of a back edge a->b is {b} plus the set of nodes that can reach a without going through b. Remove b from the flow graph, find all predecessors of a Theorem: two natural loops are either disjoint, identical, or nested. Fall 2011 “Advanced Compiler Techniques” 34

Example: Natural Loops 1 2 4 5 Natural loop of 5 -> 1 Fall 2011 3 Natural loop of 3 -> 2 “Advanced Compiler Techniques” 35

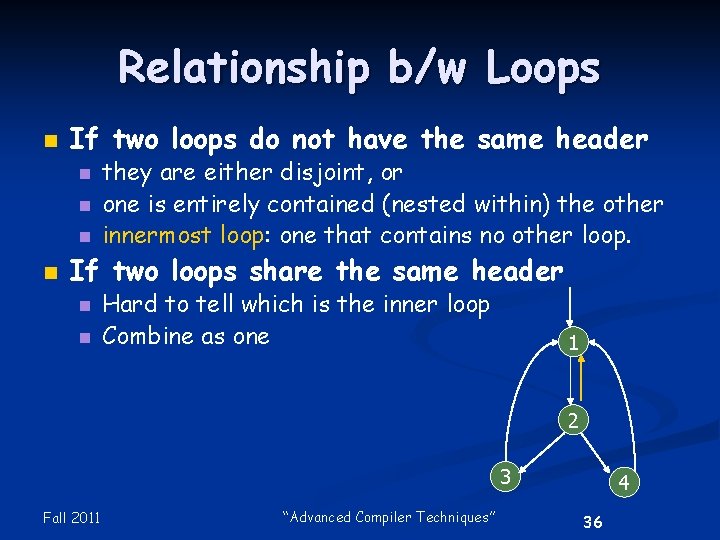
Relationship b/w Loops n If two loops do not have the same header n n they are either disjoint, or one is entirely contained (nested within) the other innermost loop: one that contains no other loop. If two loops share the same header n n Hard to tell which is the inner loop Combine as one 1 2 3 Fall 2011 “Advanced Compiler Techniques” 4 36

Next Time n Single Static Assignment (SSA) n Fall 2011 Readings: Cytron'91, Chow'97 “Advanced Compiler Techniques” 37