Schneidrahmen Componentbased implementation of a dynamic optimization algorithm

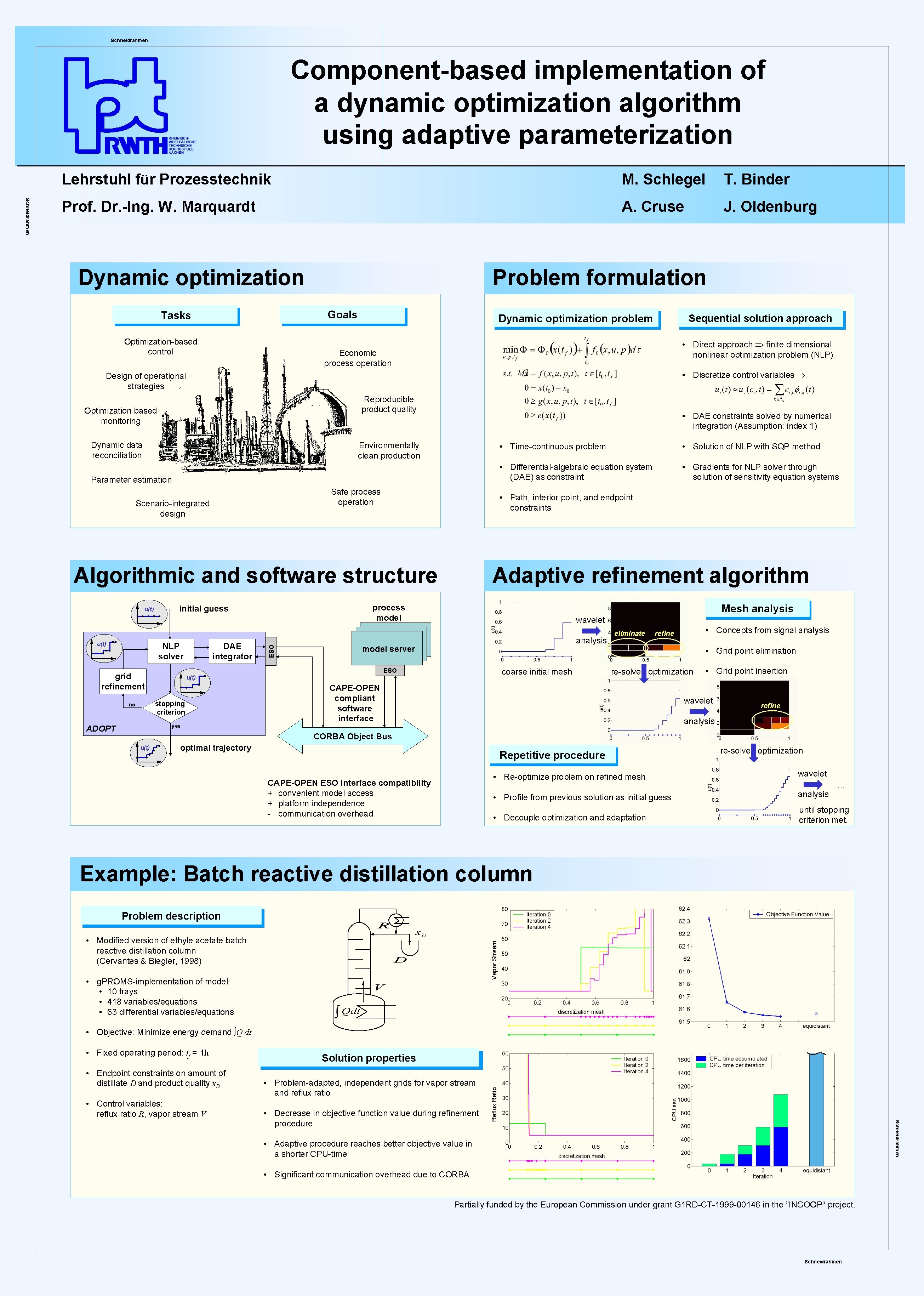
Schneidrahmen Component-based implementation of a dynamic optimization algorithm using adaptive parameterization M. Schlegel T. Binder Prof. Dr. -Ing. W. Marquardt A. Cruse J. Oldenburg Dynamic optimization Problem formulation Goals Tasks Optimization-based control Sequential solution approach Dynamic optimization problem • Direct approach finite dimensional nonlinear optimization problem (NLP) Economic process operation • Discretize control variables Design of operational strategies Reproducible product quality Optimization based monitoring Dynamic data reconciliation • DAE constraints solved by numerical integration (Assumption: index 1) Environmentally clean production Parameter estimation Safe process operation Scenario-integrated design u(t) DAE integrator yes ADOPT • Gradients for NLP solver through solution of sensitivity equation systems Mesh analysis wavelet analysis model server eliminate • Concepts from signal analysis refine • Grid point elimination coarse initial mesh u(t) stopping criterion no • Differential-algebraic equation system (DAE) as constraint Adaptive refinement algorithm ESO grid refinement • Solution of NLP with SQP method process model initial guess NLP solver • Time-continuous problem • Path, interior point, and endpoint constraints Algorithmic and software structure ESO re-solve optimization CAPE-OPEN compliant software interface • Grid point insertion wavelet refine analysis CORBA Object Bus u(t) optimal trajectory Repetitive procedure CAPE-OPEN ESO interface compatibility + convenient model access + platform independence - communication overhead re-solve optimization • Re-optimize problem on refined mesh wavelet • Profile from previous solution as initial guess analysis • Decouple optimization and adaptation until stopping criterion met. … Example: Batch reactive distillation column Problem description Vapor Stream • Modified version of ethyle acetate batch reactive distillation column (Cervantes & Biegler, 1998) • g. PROMS-implementation of model: • 10 trays • 418 variables/equations • 63 differential variables/equations • Objective: Minimize energy demand Q dt • Fixed operating period: tf = 1 h • Endpoint constraints on amount of distillate D and product quality x. D • Control variables: reflux ratio R, vapor stream V Solution properties • Problem-adapted, independent grids for vapor stream and reflux ratio Schneidrahmen • Decrease in objective function value during refinement procedure Reflux Ratio Schneidrahmen Lehrstuhl für Prozesstechnik • Adaptive procedure reaches better objective value in a shorter CPU-time • Significant communication overhead due to CORBA Partially funded by the European Commission under grant G 1 RD-CT-1999 -00146 in the ”INCOOP“ project. Schneidrahmen