Schema Refinement and Normalization Zachary G Ives University

Schema Refinement and Normalization Zachary G. Ives University of Pennsylvania CIS 550 – Database & Information Systems September 25, 2003 Some slide content courtesy of Susan Davidson & Raghu Ramakrishnan

Administrivia § § HW 2 due now HW 3 handed out Readings on XML: papers rather than textbook Will shortly have readings for each project group § Q: Dinkar’s office hours conflict with 505 on Monday. Would you prefer them on Friday? 2

Schema Refinement & Design Theory § ER Diagrams give us a start in logical schema design § Sometimes need to refine our designs further § There’s a system and theory for this § Focus is on redundancy of data Causes update, insertion, deletion anomalies 3

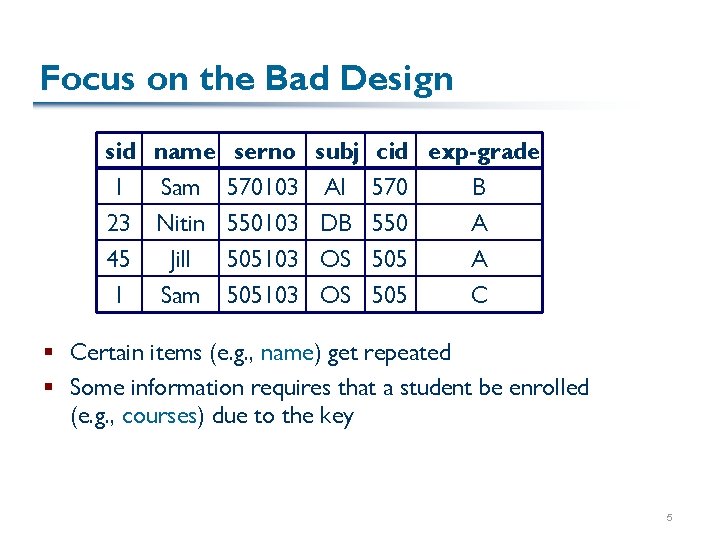
Not All Designs are Equally Good Why is this a poor schema design? Stuff(sid, name, serno, subj, cid, exp-grade) And why is this one better? Student(sid, name) Course(serno, cid) Subject(cid, subj) Takes(sid, serno, exp-grade) 4

Focus on the Bad Design sid name serno subj cid exp-grade 1 Sam 570103 AI 570 B 23 Nitin 550103 DB 550 A 45 Jill 505103 OS 505 A 1 Sam 505103 OS 505 C § Certain items (e. g. , name) get repeated § Some information requires that a student be enrolled (e. g. , courses) due to the key 5

Functional Dependencies Describe “Key-Like” Relationships A key is a set of attributes where: If keys match, then the tuples match A functional dependency (FD) is a generalization: If an attribute set determines another, written A ! B then if two tuples agree on attribute set A, they must agree on B: sid ! name What other FDs are there in this data? Ø FDs are independent of our schema design choice 6

Formal Definition of FD’s Def. Given a relation schema R and subsets X, Y of R: An instance r of R satisfies FD X Y if, for any two tuples t 1, t 2 2 r, t 1[X ] = t 2[X] implies t 1[Y] = t 2[Y] § For an FD to hold for schema R, it must hold for every possible instance of r (Can a DBMS verify this? Can we determine this by looking at an instance? ) 7

General Thoughts on Good Schemas We want all attributes in every tuple to be determined by the tuple’s key attributes, i. e. part of a superkey (for key X Y, a superkey is a “non-minimal” X) What does this say about redundancy? But: § What about tuples that don’t have keys (other than the entire value)? § What about the fact that every attribute determines itself? 8

Armstrong’s Axioms: Inferring FDs Some FDs exist due to others; can compute using Armstrong’s axioms: § Reflexivity: If Y X then X Y (trivial dependencies ) name, sid name § Augmentation: If X Y then XW YW serno subj so serno, exp-grade subj, exp-grade § Transitivity: If X Y and Y Z then X Z serno cid and cid subj so serno subj 9

Armstrong’s Axioms Lead to… If X Y and X Z then X YZ § Pseudotransitivity: If X Y and WY Z then XW Z § Decomposition: If X Y and Z Y then X Z § Union: Let’s prove these from Armstrong’s Axioms 10

Closure of a Set of FD’s Defn. Let F be a set of FD’s. Its closure , F +, is the set of all FD’s: {X Y | X Y is derivable from F by Armstrong’s Axioms} Which of the following are in the closure of our Student. Course FD’s? name cid subj serno subj cid, sid subj cid sid 11

Attribute Closures: Is Something Dependent on X? Defn. The closure of an attribute set X, X+, is: X+ = {Y | X Y F +} § This answers the question “is Y determined (transitively) by X? ”; compute X+ by: closure : = X; repeat until no change { if there is an FD U V in F such that U is in closure then add V to closure} § Does sid, serno subj, exp-grade? 12

Equivalence of FD sets Defn. Two sets of FD’s, F and G, are equivalent if their closures are equivalent, F + = G + e. g. , these two sets are equivalent: {XY Z, X Y} and {X Z, X Y} § F + contains a huge number of FD’s (exponential in the size of the scheme) § Would like to have smallest “representative” FD set 13

Minimal Cover we express Defn. A FD set F is minimal if: each FD in 1. Every FD in F is of the form X A, simplest form where A is a single attribute 2. For no X A in F is: in a sense, F – {X A } equivalent to F each FD is “essential” 3. For no X A in F and Z X is: to the cover F – {X A } {Z A } equivalent to F Defn. F is a minimum cover for G if F is minimal and is equivalent to G. e. g. , {X Z, X Y} is a minimal cover for {XY Z, X Y} 14

More on Closures If F is a set of FD’s and X Y F + then for some attribute A Y, X A F + Proof by counterexample. Assume otherwise and let Y = {A 1, . . . , An} Since we assume X A 1, . . . , X An are in F + then X A 1. . . An is in F + by union rule, hence, X Y is in F + which is a contradiction 15

Why Armstrong’s Axioms? Why are Armstrong’s axioms (or an equivalent rule set) appropriate for FD’s? They are: § Consistent : any relation satisfying FD’s in F will satisfy those in F + § Complete : if an FD X Y cannot be derived by Armstrong’s axioms from F, then there exists some relational instance satisfying F but not X Y Ø In other words, Armstrong’s axioms derive all the FD’s that should hold 16

Proving Consistency We prove that the axioms’ definitions must be true for any instance, e. g. : § For augmentation (if X Y then XW YW): If an instance satisfies X Y, then: § For any tuples t 1, t 2 r, if t 1[X] = t 2[X] then t 1[Y] = t 2[Y] by defn. § If, additionally, it is given that t 1[W] = t 2[W], then t 1[YW] = t 2[YW] 17

Proving Completeness Suppose X Y F + and define a relational instance r that satisfies F + but not X Y: § Then for some attribute A Y, X A F + § Let some pair of tuples in r agree on X + but disagree everywhere else: X A X+ –X R – X+ – {A} x 1 x 2. . . xn a 1, 1 v 2. . . vm w 1, 1 w 2, 1. . . x 1 x 2. . . xn a 1, 2 v 1 v 2. . . vm w 1, 2 w 2, 2. . . 18

Proof of Completeness cont’d § Clearly this relation fails to satisfy X A and X Y. We also have to check that it satisfies any FD in F +. § The tuples agree on only X +. Thus the only FD’s that might be violated are of the form X’ Y’ where X’ X+ and Y’ contains attributes in R – X + – {A}. § But if X’ Y’ F+ and X’ X+ then Y’ X+ (reflexivity and augmentation). Therefore X’ Y’ is satisfied. 19

Decomposition § Consider our original “bad” attribute set Stuff(sid, name, serno, subj, cid, exp-grade) § We could decompose it into Student(sid, name) Course(serno, cid) Subject(cid, subj) § But this decomposition loses information about the relationship between students and courses. Why? 20

Lossless Join Decomposition R 1, … Rk is a lossless join decomposition of R w. r. t. an FD set F if for every instance r of R that satisfies F, ÕR 1(r) ⋈. . . ⋈ ÕRk(r) = r Consider: sid name serno subj cid exp-grade 1 23 Sam Nitin 570103 550103 AI DB 570 550 B A What if we decompose on (sid, name) and (serno, subj, cid, exp-grade)? 21

Testing for Lossless Join R 1, R 2 is a lossless join decomposition of R with respect to F iff at least one of the following dependencies is in F+ (R 1 R 2) R 1 – R 2 (R 1 R 2) R 2 – R 1 So for the FD set: sid name serno cid, exp-grade cid subj Is (sid, name) and (serno, subj, cid, exp-grade) a lossless decomposition? 22

Dependency Preservation Ensures we can “easily” check whether a FD X Y is violated during an update to a database: § The projection of an FD set F onto a set of attributes Z, F Z is {X Y | X Y F +, X Y Z} i. e. , it is those FDs local to Z’s attributes § A decomposition R 1, …, Rk is dependency preserving F + = (F R 1 . . . F R k)+ if The decomposition hasn’t “lost” any essential FD’s, so we can check without doing a join 23

Example of Lossless and Dependency-Preserving Decompositions Given relation scheme R(name, street, city, st, zip, item, price) And FD set name street, city st street, city zip name, item price Consider the decomposition R 1(name, street, city, st, zip) and R 2(name, item, price) Ø Is it lossless? Ø Is it dependency preserving? What if we replaced the first FD by name, street city? 24

Another Example Given scheme: R(sid, fid, subj) and FD set: fid subj sid, subj fid Consider the decomposition R 1(sid, fid) and R 2(fid, subj) Ø Is it lossless? Ø Is it dependency preserving? 25

FD’s and Keys § Ideally, we want a design s. t. for each nontrivial dependency X Y, X is a superkey for some relation schema in R § We just saw that this isn’t always possible § Hence we have two kinds of normal forms 26

Two Important Normal Forms Boyce- Codd Normal Form (BCNF). For every relation scheme R and for every X A that holds over R, either A X (it is trivial) , or or X is a superkey for R Third Normal Form (3 NF). For every relation scheme R and for every X A that holds over R, either A X (it is trivial), or X is a superkey for R, or A is a member of some key for R 27

Normal Forms Compared § BCNF is preferable, but sometimes in conflict with the goal of dependency preservation § It’s strictly stronger than 3 NF § Let’s see algorithms to obtain: § A BCNF lossless join decomposition § A 3 NF lossless join, dependency preserving decomposition 28

BCNF Decomposition Algorithm (from. Korth et al. ; our book gives recursive version) result : = {R} compute F+ while there is a schema Ri in result that is not in BCNF { let A B be a nontrivial FD on Ri s. t. A Ri is not in F+ and A and B are disjoint } result: = (result – Ri) {(Ri - B), (A, B)} 29

3 NF Decomposition Algorithm Let F be a minimal cover i: =0 for each FD A B in F { if none of the schemas Rj, 1 j i, contains AB { increment i Ri : = (A, B) } } if no schema Rj, 1 j i contains a candidate key for R { increment i Ri : = any candidate key for R } return (R 1, …, Ri) Build dep. preserving decomp. Ensure lossless decomp. 30

Summary § We can always decompose into 3 NF and get: § Lossless join § Dependency preservation § But with BCNF we are only guaranteed lossless joins § BCNF is stronger than 3 NF: every BCNF schema is also in 3 NF § The BCNF algorithm is nondeterministic, so there is not a unique decomposition for a given schema R 31