Schema per affrontare la risoluzione di un problema

Schema per affrontare la risoluzione di un problema 0) Vincere la “paura” e/o la “pigrizia” 1) Prima lettura: comprendere il contesto in cui collocare il problema 2) Seconda lettura: leggere attentamente evidenziando ipotesi (dati e condizioni) e tesi (incognita, richieste) 3) Schematizzare o disegnare i legami esistenti tra dati e richieste 4) Dimostrazione: individuare gli strumenti e le conoscenze adeguati a soddisfare la / le richieste del problema 5) Formalizzare: tradurre in linguaggio simbolico la/ le relazioni tra dati e incognite 6) risolvere il problema con un metodo efficace 7) verificare la correttezza delle soluzioni: il risultato è sensato? 8) Ricercare eventuali percorsi risolutivi più efficaci

Leggere il testo con attenzione I quattro personaggi rappresentati sono sepolti fino al collo, non possono muoversi e possono vedere solo ciò che sta davanti a loro. Tra il primo a sinistra e gli altri c’è un alto muro. Tutti sanno che ognuno di loro indossa un cappello, e che i cappelli sono due bianchi e due neri. Avranno tutti salva la vita soltanto se uno di loro, entro qualche minuto, riuscirà a dire di che colore è il cappello che ha in testa. Qualcuno parlerà? E cosa dirà?

soluzione Il secondo aspetta qualche minuto e non sente parlare il terzo quindi capisce di avere il cappello diverso dal primo e dice “NERO”.

Comprendere un testo di geometria individuare subito gli oggetti che si possono visualizzare trascurando temporaneamente quelli meno chiari. Successivamente cercare di capire in che relazione stanno tali oggetti Vediamo questo esempio : "È data una sfera di diametro AB = 2 r. Determinare sul diametro di questa sfera un segmento AC = x in modo che conducendo da C il piano perpendicolare al diametro, la somma della superficie della zona la cui altezza è AC e della superficie laterale del cono DOE avente per vertice il centro O della sfera e per base la sezione formata dall’intersezione tra piano e sfera, sia uguale a a 2"

Come procedere gli oggetti immediatamente individuabili in una prima lettura potrebbero essere una sfera, il suo diametro, un piano perpendicolare al diametro e un cono. Sistemando poi le lettere sulla figura possiamo cominciare a montare insieme gli oggetti individuati: A e B sono gli estremi del diametro, C un punto di tale diametro, il piano deve passare per C, ecc. … A volte per comprendere, arrivati in fondo alla frase, dobbiamo fare il percorso inverso.

rappresentare un problema una corretta rappresentazione del problema aiuta a pervenire alla sua soluzione. In alcuni casi, rappresentare correttamente il problema porta a una soluzione immediata, come nel seguente esempio: PROBLEMA Se si tolgono a una scacchiera regolare il quadratino in alto a destra e quello in basso a sinistra, è possibile ricoprire i restanti 62 quadratini con 33 pezzi del domino? (Notare che ciascun pezzo del domino occupa esattamente 2 quadratini. )

Soluzione La risposta è no Ciò è immediatamente evidente se si colorano i quadratini della scacchiera di nero e di bianco si osserva che i due quadratini sottratti alla scacchiera sono entrambi dello stesso colore, ad esempio bianchi, e quindi restano sulla scacchiera 31 quadratini bianchi e 33 quadratini neri. D'altra parte, ciascun domino copre esattamente un quadratino bianco e uno nero; perciò, il problema è insolubile.

La dimostrazione come atto creativo Le soluzioni inconsuete Questi problemi mettono a dura prova la nostra inventiva. Richiedono una certa capacità di inventare soluzioni o ragionamenti inconsueti. Ci aiutano a mettere in campo il pensiero produttivo cioè l'insieme dei processi che portano la mente a produrre procedure nuove rispetto a ciò che è stato imparato

Problema Su di un tavolo, troviamo una candela, dei fiammiferi e una scatola di puntine; vogliamo costruire con essi una fonte di luce che sia solidale con una porta, e quindi si muova quando la porta viene aperta o chiusa

Soluzione In questo caso, la soluzione del problema consiste nello svuotare la scatola, attaccarla alla porta con due puntine, e usarla come porta -lampada, ponendo su di essa la candela. Questa soluzione richiede di cambiare il ruolo della scatola, che da contenitore delle puntine, apparentemente inutile, diviene parte essenziale della soluzione. Ciò però richiede una certa dose di inventiva.

Vediamo ora un altro esempio: Dal soffitto pendono due corde, e il problema consiste nel collegarle. Purtroppo, le due corde distano tra loro così tanto da non riuscire, con le braccia aperte, a prenderle entrambe. Abbiamo a disposizione una sedia e delle forbici; come fare?

Soluzione Anche in questo caso, la soluzione del problema non è convenzionale. Vari soggetti si ostinano a usare la sedia per avvicinare in qualche modo le corde (che, notoriamente, cadono verticalmente dal soffitto, e quindi restano alla stessa distanza fra loro anche se ci mettiamo in piedi sulla sedia). Altre strategie prevedono di tagliare pezzi di fune da una parte e annodarli dall'altra, ma anch'esse non funzionano. La soluzione del problema consiste nel legare le forbici a una delle corde e costruire così un pendolo, che viene fatto oscillare. In questo modo, è possibile prendere l'altro capo della corda, spostarsi verso il centro della stanza, e afferrare al volo il pendolo, collegando le due corde. L'aspetto non intuitivo della soluzione consiste nell'usare le forbici non per tagliare le corde, come sarebbe naturale, bensì come peso, per generare le oscillazioni.

Dimostrazione Dopo aver individuato l'obiettivo da raggiungere, si devono mettere in campo tutte le risorse per arrivare allo scopo: Non ci sono regole automatiche. Evita stereotipi del tipo: Un problema si risolve in 10 minuti. Corollario : dopo 10 minuti abbandona Nei problemi vanno applicate le conoscenze appena studiate. Corollario: se non le ricordi, lascia perdere. La matematica formale ha poco a che fare con il reale: Corollario: ignorala quando devi risolvere un problema

Formalizzare Il prodotto di tre numeri interi consecutivi è sempre divisibile per due e per tre. Dire, giustificando la risposta se n 3 -n è divisibile per 6,

Valutare se i risultati sono sensati v

GLI AMICI MATEMATICI Due amici, John e Paul, entrambi matematici, si incontrano dopo anni, e si scambiano domande sulle rispettive famiglie. “Quanti figli hai adesso, e quanti anni hanno? ” chiede John all’amico. “Ho tre figli” risponde Paul. “Il prodotto delle loro età è 36 e la somma delle loro età è uguale al numero di quel tram che sta passando”. “Le informazioni che mi hai dato non bastano a farmi conoscere le età dei tuoi figli!” replica John dopo qualche istante. Oh, perdonami, hai ragione! Ti dirò anche questo: il maggiore ha gli occhi verdi”, fa Paul. Sapresti dire quanti anni hanno i tre figli di Paul?

La somma non è sufficiente poiché ci sono due possibilità allora l’informazione in più dice che il grande non è gemello: l’unico caso di due possibilità è la somma 13 quindi le età sono 2, 2 9.

I figli della vicina “La vicina di casa ha dei figli: l’età del minore è la metà dell’età del maggiore e il prodotto di tutte le età è 1664. Quanti sono i figli della vicina? ”

Soluzione La scomposizione di 1664 è 27 13. Occorre che 27 sia il prodotto dell’età del più piccolo e del più grande: l’unica possibilità è che il minore abbia 23 = 8 anni e il maggiore abbia 24 = 16 anni. Infatti 23 è la metà di 24. La vicina ha tre figli.

Dividere in gruppi Il prof di matematica vuole dividere gli alunni della classe in gruppi di tre ma rimane un alunno da solo, allora tenta di dividere in gruppi da quattro ma rimangono due alunni. Infine divide in gruppi da cinque ma ne rimangono ne restano ancora due: di quanti alunni è composta la classe?

Soluzione Il numero cercato diviso 3 dà resto 1: 4; 7; 10; 13; 16; 19; 22; 25; … diviso 4 dà resto 2: 6; 10; 14; 18; 22; 26; … diviso 5 dà resto 2: 7; 12; 17; 22; 27; … La classe è composta di 22 alunni

La Palestra “L’insegnante di educazione fisica, per un problema di spazio, ha detto che avrebbe portato in palestra metà della classe più mezzo studente. Alle proteste degli altri, l’insegnante ha risposto che la settimana successiva avrebbe portato in palestra metà dei rimanenti più mezzo studente, e nella terza settimana avrebbe portato i rimanenti. Di quanti alunni potrebbe essere composta la classe? ”

Soluzione Quando possiamo dire mezzo alunno? n n/2+1/2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 (n-n/2+1/2)/2+1/2 2 2, 5 3 3, 5 4 4, 5 5 5, 5 6 6, 5 7 7, 5 8 8, 5 9 9, 5 10 10, 5 11 11, 5 12 12, 5 13 13, 5 14 14, 5 15 15, 5 16 16, 5 17 17, 5 18 18, 5 19 n-(n/2+n/4+1) 1, 5 1, 75 2 2, 25 2, 75 3 3, 25 3, 75 4 4, 25 4, 75 5 5, 25 5, 75 6 6, 25 6, 75 7 7, 25 7, 75 8 8, 25 8, 75 9 9, 25 9, 75 10 -0, 5 -0, 25 0, 75 1 1, 25 1, 75 2 2, 25 2, 75 3 3, 25 3, 75 4 4, 25 4, 75 5 5, 25 5, 75 6 6, 25 6, 75 7 7, 25 7, 75 8

Risolvere problemi con le equazioni Un elefante e un topo pesano insieme una tonnellata e un etto. L’elefante pesa una tonnellata in più del topo. Quanto pesa il topo? ”

Scriviamo i dati in linguaggio simbolico P: peso dell’elefante p: peso del topo Convertiamo le tonnellate e l’etto in Kg. 1 ton=1000 Kg 1 hg=0, 1 Kg P+p=1000, 1 Kg p=x (incognita) P=p+1000 Kg Consideriamo la prima delle equazioni che abbiamo scritto: P+p=1000, 1 Kg Quante incognite, cioè grandezze di cui non si conosce il valore, contiene? Contiene due incognite, P e p Non è possibile risolvere un’equazione in due incognite, occorre eliminarne una. La variabile da eliminare è quella che non ci interessa, cioè la P.

Scriviamo l’equazione utilizzando l’incognita x Utilizziamo la seconda informazione: L’elefante pesa una tonnellata in più del topo. Scritta in linguaggio simbolico: P=p+1000 Kg Poiché P è uguale alla somma p+1000 kg, possiamo sostituire al suo posto questa espressione nella prima equazione : P+p=1000, 1 Kg p+1000 kg+p=1000, 1 kg Ricordiamo che p=x (incognita), quindi: x+1000 kg+x=1000, 1 kg Risolvendo l’equazione si ottiene x=0, 05 kg Il topolino pesa 0, 05 kg. Convertiamo questa misura in grammi 0, 05 kg=50 g Sommando il peso dell’elefante e quello del topolino si deve ottenere 1 tonnellata e 1 etto: 1000, 05 kg+0, 05 kg=1000, 1 kg.

Giochi di magia Pensa ad un numero, raddoppialo, aggiungi cinque, togli il numero che hai pensato. Aggiungi due e togli il numero che hai pensato. Moltiplica per tre. Puoi essere sicuro del risultato?

Problema Aldo oggi compie gli anni e I parenti si riuniscono per festeggiarlo. Sua zia Bruna, che non lo vede da tempo, esclama: “ Ma come sei diventato alto!” Aldo risponde: “Lo sai zia? La mia statura in centimetri è dodici volte la mia età, ma tre anni fa ero alto tredici volte la mia età. Eppure sono cresciuto di 24 centimetri. Quanti anni ha compiuto Aldo ? (da olimpiadi di informatica 4/12/2008)

Equazioni diofantee (o indeterminate ) del tipo ax+by=c con a, b, c interi e soluzioni intere. Un negoziante acquista un certo numero di camicie da 40 euro e un certo numero di camicie da 60 euro. Ha a disposizione 560 euro. Quante camicie di un tipo e quante di un altro può acquistare ponendosi l'obiettivo di utilizzare tutta la cifra a disposizione?

Equazioni diofantee Al mercato di Rifredi con 36 euro si può comprare un maglione, una camicia e nove paia di calzini. Sapendo che due camicie costano quanto un magione e quattro paia di calzini, quanto costa ogni singolo pezzo di vestiario?

I SACCHETTI DI BIGLIE (da “Zona quiz” del Corriere della Sera) Isacco ha un negozio di giocattoli e ordina 7 piccoli sacchetti di biglie e 18 grandi sacchetti di biglie. Tutte le biglie sono uguali. Quando arriva lo scatolone, si accorge che durante il trasporto tutti i sacchetti si sono rotti e le biglie, 233 in tutto, rotolano allegramente nella scatola. Come fa Isacco a sapere quante biglie c’erano nei sacchetti piccoli e quante in quelli grandi?

SOLUZIONE Si osserva con una tabella in EXCEL che gli unici valori che danno numeri interi sono 5 e 11 o 23 e 4 ma essendo i sacchetti piccoli con meno biglie l’unica soluzione accettabile è la prima.

Sistemi Nella città di non fumo gli unici negozi sono tabaccherie e latterie. L'anno scorso le tabaccherie erano i 2/3 delle latterie; quest'anno due tabaccherie sono diventate latterie cosicchè ora le tabaccherie sono solo i 9/16 delle latterie (dall'anno scorso il numero di negozi di Nonfumo è rimasto lo stesso). Quante latterie c'erano l'anno scorso a Nonfumo? (A) 12 (B) 16 (C ) 20 (D) 30 (E) 60 (olimpiadi di matematica novembre 2009)

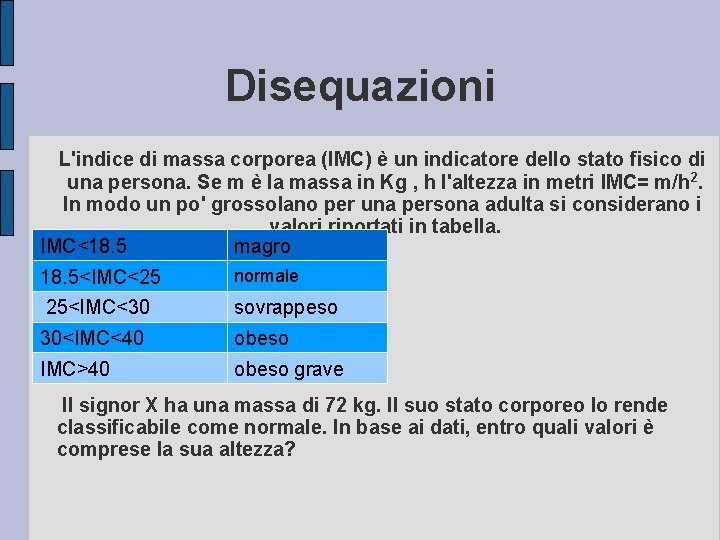
Disequazioni L'indice di massa corporea (IMC) è un indicatore dello stato fisico di una persona. Se m è la massa in Kg , h l'altezza in metri IMC= m/h 2. In modo un po' grossolano per una persona adulta si considerano i valori riportati in tabella. IMC<18. 5 magro 18. 5<IMC<25 normale 25<IMC<30 sovrappeso 30<IMC<40 obeso IMC>40 obeso grave Il signor X ha una massa di 72 kg. Il suo stato corporeo lo rende classificabile come normale. In base ai dati, entro quali valori è comprese la sua altezza?

Problemi di scelta La piscina di Acquadolce offre ai suoi frequentatori due diverse modalità di pagamento: è possibile fare un abbonamento mensile, che costa 75 euro oppure pagare un biglietto di 5 euro per ogni ingresso. Con quanti ingressi in un mese conviene fare l'abbonamento? (da prove invalsi giugno 2009)

Problemi di scelta Un'azienda agricola pugliese deve scegliere l'agenzia di trasporti più conveniente per portare il suo olio nel capoluogo da dove viene portato in treno al nord. Sul territorio ci sono due agenzie con le seguenti offerte: Agenzia SICURRAPIDO costo fisso di 230 europiù 2 euro per ogni quintale di merce trasportata Agenzia PRESTOEBENE costo fisso di 130 euro più 2. 1 euro al quintale più costo aggiuntivo inversamente proporzionale al carico trasportato. Se il camion è pieno tale costo è 20 euro. Carico massimo 500 quintali. Indica con x il numero di quintali da trasportare e con y il costo in euro. Scrivi il costo del trasporto per le due agenzie. Per quale quantità di merce le due agenzie hanno lo stesso prezzo? Indica i costi delle due agenzie per 10, 200, 400, 500 quintali. Rappresenta su un grafico i due costi e indica la scelta più conveniente in funzione della quantità di merce trasportata.