Scheduling Periodic RealTime Tasks with Heterogeneous Reward Requirements

Scheduling Periodic Real-Time Tasks with Heterogeneous Reward Requirements I-Hong Hou and P. R. Kumar 1

Problem Overview � Imprecise Computation Model: � Tasks generate jobs periodically, each job with some deadline � Jobs that miss deadline cause performance degradation of the system, rather than timing fault � Partially-completed jobs are still useful and generate some rewards � Previous tasks work: maximize the total rewards of all � Assumes that rewards of different tasks are equivalent � May result in serious unfairness � Does not allow tradeoff between tasks � This 2 task work: Provide guarantees on reward for each

Example: Video Streaming �A server serves several video streams � Each stream generates a group of frames (GOF) periodically � Frames need to be delivered on time, or they are not useful � Lost frames result in glitches of videos � Frames of the same flow are not equally important � MPEG has three types of frames: I, P, and B � I-frames are more important than P-frames, which are more important than B-frames � Goal: provide guarantees on perceived video quality for each stream 3

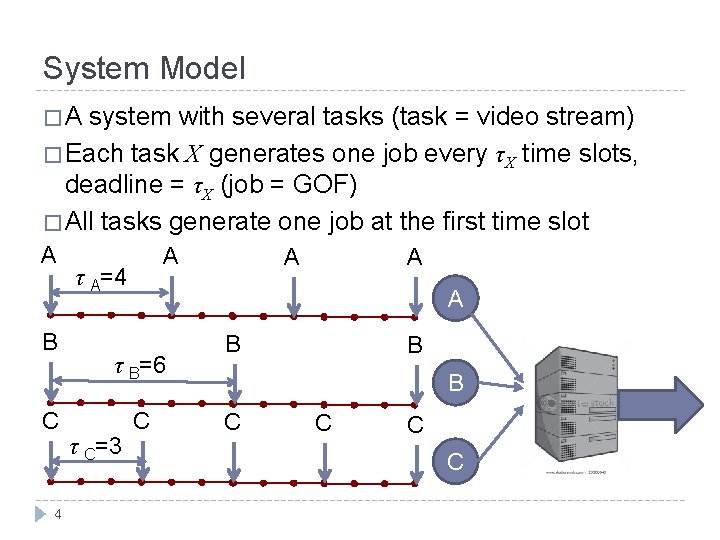
System Model �A system with several tasks (task = video stream) � Each task X generates one job every τX time slots, deadline = τX (job = GOF) � All tasks generate one job at the first time slot A B C 4 A τ A=4 A τ B=6 τ C=3 A A C B B B C C

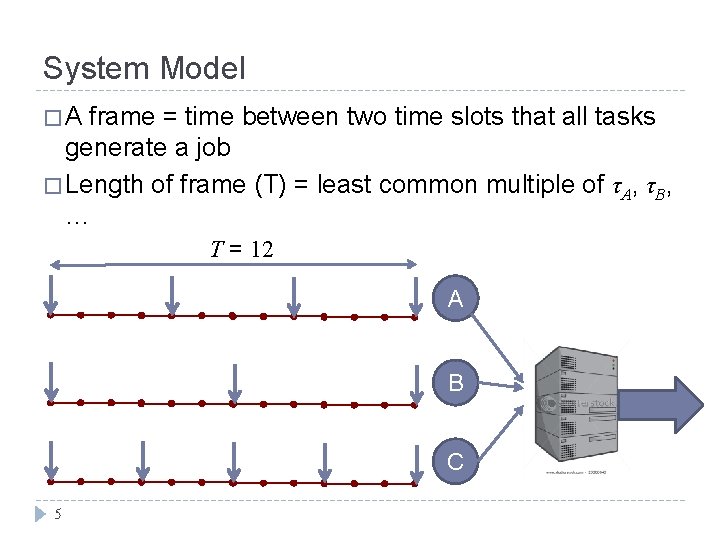
System Model �A frame = time between two time slots that all tasks generate a job � Length of frame (T) = least common multiple of τA, τB, … T = 12 A B C 5

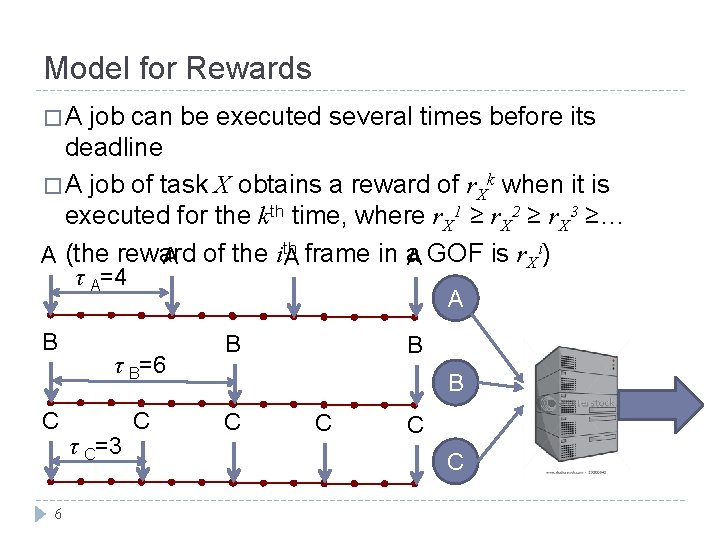
Model for Rewards �A job can be executed several times before its deadline � A job of task X obtains a reward of r. Xk when it is executed for the kth time, where r. X 1 ≥ r. X 2 ≥ r. X 3 ≥… A (the reward A of the ith A GOF is r. Xi) A frame in a τ A=4 B C 6 A τ B=6 τ C=3 C B B B C C

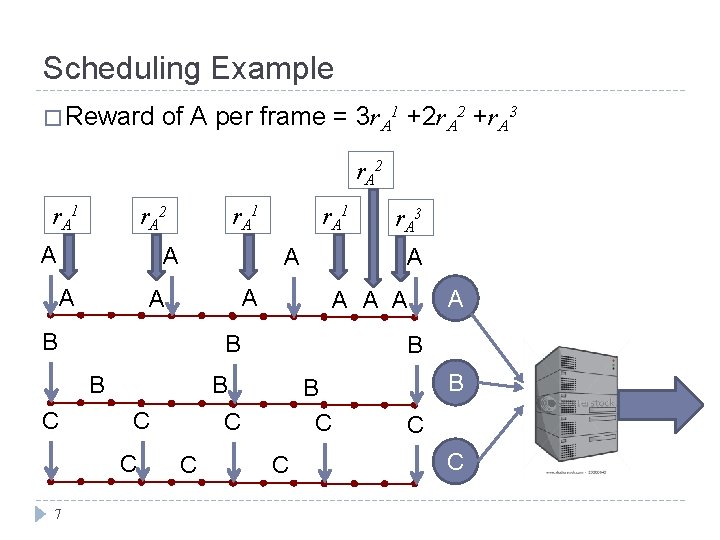
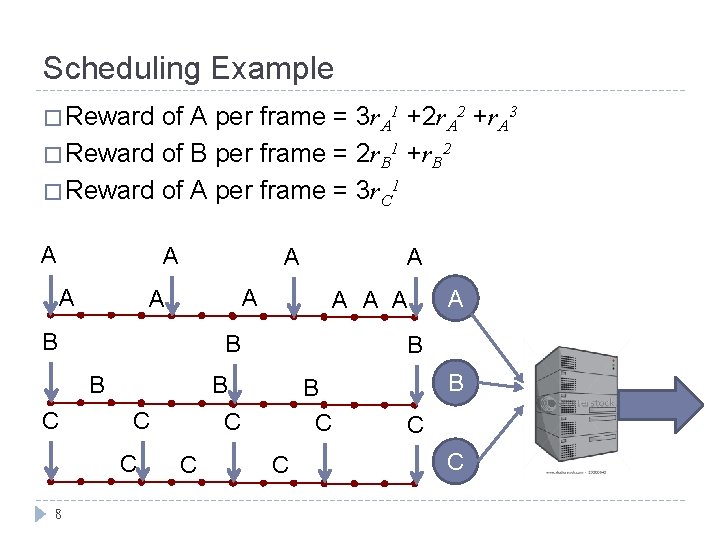
Scheduling Example � Reward of A per frame = 3 r. A 1 +2 r. A 2 +r. A 3 r. A 2 r. A 1 r. A 2 A A A C B C C C A B B C 7 A A A B B r. A 3 A A B C r. A 1 C B C C

Scheduling Example � Reward of A per frame = 3 r. A 1 +2 r. A 2 +r. A 3 � Reward of B per frame = 2 r. B 1 +r. B 2 � Reward of A per frame = 3 r. C 1 A A A B C C C A B B C 8 A A A B B C A A C B C C

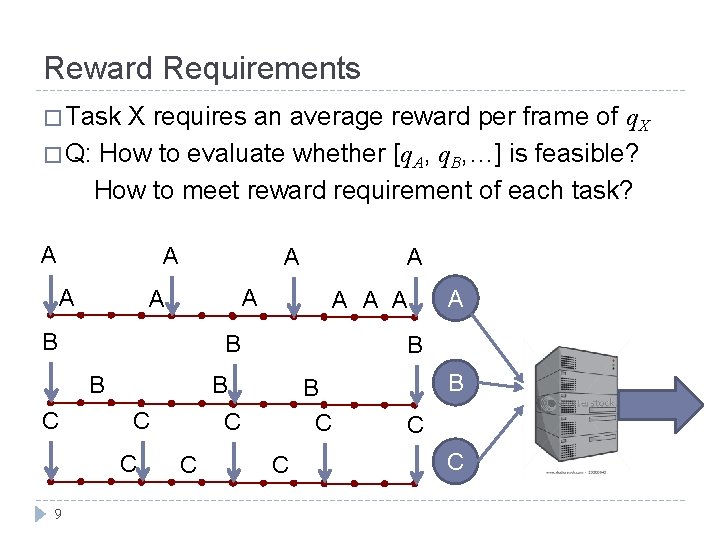
Reward Requirements � Task X requires an average reward per frame of q. X � Q: How to evaluate whether [q. A, q. B, …] is feasible? How to meet reward requirement of each task? A A A B C C C A B B C 9 A A A B B C A A C B C C

Extension for Imprecise Computation Models � Imprecise Computation Model: Each job may have a mandatory part and an optional part � Mandatory part needs to be completed, or results in a timely fault � Incomplete optional part only reduces performance � Our model: set the reward of a mandatory part to be M, where M is larger than any finite number � The reward requirement of a task = a. M+b, where a is the number of mandatory parts, and b is the requirements on optional parts � Fulfill reward requirement ensures that all mandatory parts are completed on time 10

Feasibility Condition : = average number of jobs of X that are executed at least i times per frame � Obviously, 0 ≤ f. Xi ≤ T/τX � f Xi � Average reward of X = ∑i f. Xir. Xi � Average reward requirement: ∑i f. Xir. Xi ≥ q. X � The average number of time slots that the server spends on X per frame = ∑i f. Xi � Hence, ∑X ∑i f. Xi ≤ T 11

Admission Control � Theorem: A system is feasible if and only if there exists a vector [ f. Xi ]such that 1. 0 ≤ f. Xi ≤ T/τX 2. ∑i f. Xir. Xi ≥ q. X 3. ∑X ∑i f. Xi ≤ T � Check feasibility by linear programming � Complexity of admission control can be further reduced by noting r. X 1 ≥ r. X 2 ≥ r. X 3 ≥… � Theorem: check feasibility in O(∑X τX) time 12

Scheduling Policy � Q: Given a feasible system, how to design a policy that fulfill all reward requirements? � Propose a framework for designing policies � Propose an on-line scheduling policy � Analyze the performance of the on-line scheduling policy 13

A Condition Based on Debts � Let s. X(k) be the reward obtained by X in the kth frame � Debt of task X in the kth frame: d. X(k) = [d. X(k-1)+q. X - s. X(k)]+ � x+ : = max{x, 0} � The requirement of task X is met if d. X(k)/k→ 0, as k→∞ � Theorem: A policy that maximizes ∑X d. X(k)s. X(k) for every frame fulfills every feasible system � Such 14 a policy is called a feasibility optimal policy

Approximation Policy � Computation overhead of a feasibility optimal policy may be high � Study performance guarantees of suboptimal policies � Theorem: A policy whose resulting ∑X d. X(k)s. X(k) is at least 1/p of the resulting ∑X d. X(k)s. X(k) by an optimal policy, then this policy achieves reward requirement [q. X] if the reward requirement [pq. X] is feasible � Such 15 a policy is called a p-approximation policy

An On-Line Scheduling Policy � At some time slot, let ( j. X -1) be the number of times that the server has worked on the current job of X � If the server schedules X in this time slot, X obtains a reward of r. Xj. X � Greedy Maximizer: Schedule the task X that maximizes r. Xj. X d. X(k) in every time slot � Greedy 16 Maximizer can be efficiently implemented

Performance of Greedy Maximizer � The Greedy Maximizer is feasibility optimal when the period length of all tasks are the same � τA = τB =… � However, when tasks have different period lengths, the Greedy Maximizer is not feasibility optimal 17

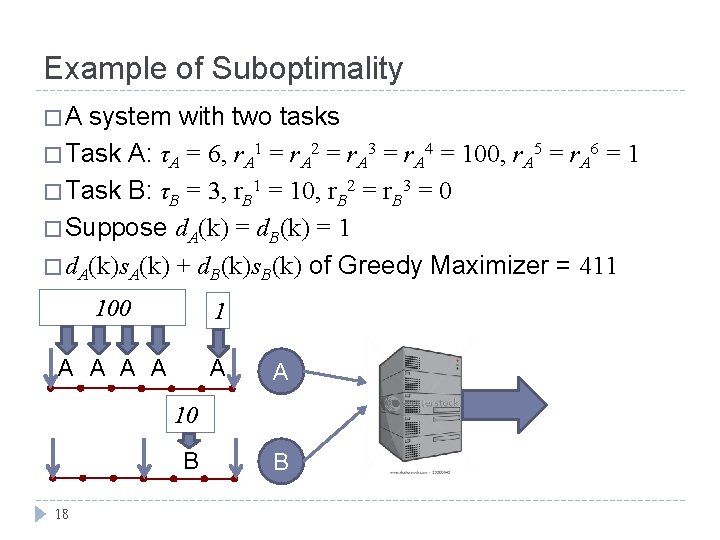
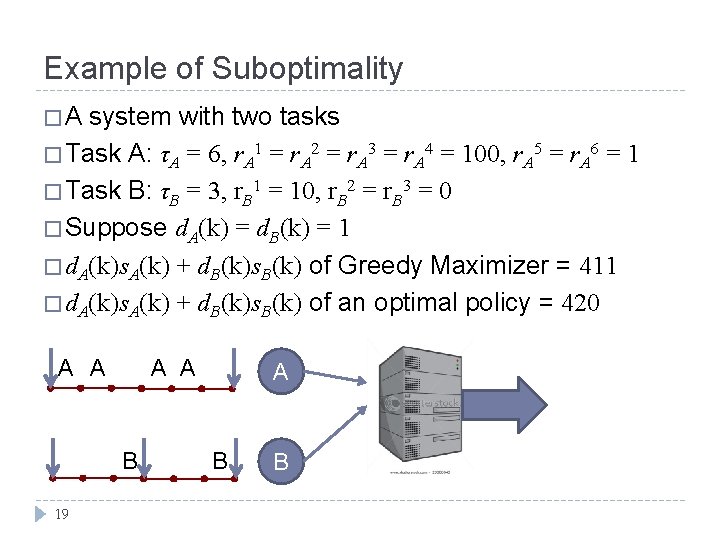
Example of Suboptimality �A system with two tasks � Task A: τA = 6, r. A 1 = r. A 2 = r. A 3 = r. A 4 = 100, r. A 5 = r. A 6 = 1 � Task B: τB = 3, r. B 1 = 10, r. B 2 = r. B 3 = 0 � Suppose d. A(k) = d. B(k) = 1 � d. A(k)s. A(k) + d. B(k)s. B(k) of Greedy Maximizer = 411 100 1 A A A 10 B 18 B

Example of Suboptimality �A system with two tasks � Task A: τA = 6, r. A 1 = r. A 2 = r. A 3 = r. A 4 = 100, r. A 5 = r. A 6 = 1 � Task B: τB = 3, r. B 1 = 10, r. B 2 = r. B 3 = 0 � Suppose d. A(k) = d. B(k) = 1 � d. A(k)s. A(k) + d. B(k)s. B(k) of Greedy Maximizer = 411 � d. A(k)s. A(k) + d. B(k)s. B(k) of an optimal policy = 420 A A B 19 A B B

Approximation Bound � Analyze the worst case performance of the Greedy Maximizer � Show that resulting ∑X d. X(k)s. X(k) is at least 1/2 of the resulting ∑X d. X(k)s. X(k) by any other policy � Theorem: The Greedy Maximizer is a 2 approximation policy � The Greedy Maximizer achieves reward requirements [q. X] as long as requirements [2 q. X] are feasible 20

Simulation Setup: MPEG Streaming � MPEG: 1 GOF consists of 1 I-frame, 3 P-frames, and 8 B-frames � Two groups of tasks, A and B � Tasks in A treat both I-frames and P-frames as mandatory parts, while tasks in B only require Iframes to be mandatory � B-frames are optional for tasks in A; both P-frames and Bframes are optional for tasks in B � 3 21 tasks in each group

Reward Function for Optional Part � Each task gains some reward when its optional parts are executed � Consider three types of optional part reward functions: exponential, logarithmic, and linear � Exponential: X obtains a total reward of (5+k)(1 -e-i/5) if its job is executed i times, where k is the index of the task X � Logarithmic: X obtains a total reward of (5+k)log(10 i+1) if its job is executed i times � Linear: X obtains a total reward of (5+k)i if its job is executed i times 22

Performance Comparison � Assume all tasks in A requires an average reward of α, and all tasks in B requires an average reward of β � Plot all pairs of (α, β) that are achieved by each policy � Consider three policies: � Feasible: the feasible region characterized by the feasibility conditions � Greedy Maximizer � MAX: a policy that aims to maximize the total reward in the system 23

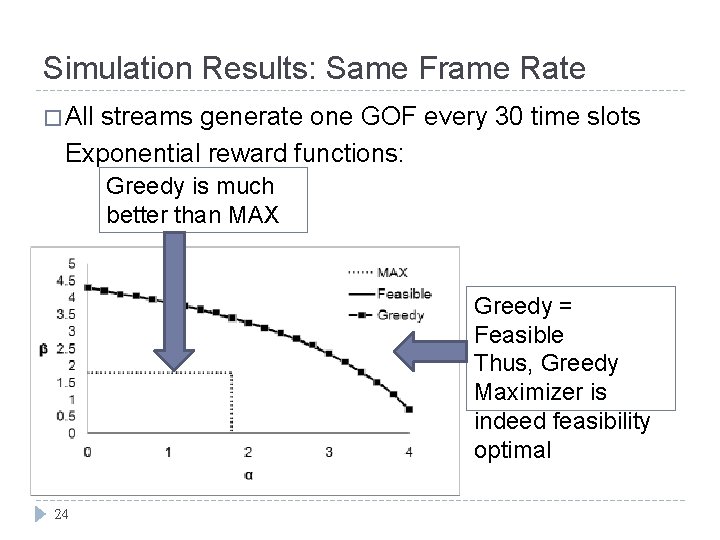
Simulation Results: Same Frame Rate � All streams generate one GOF every 30 time slots Exponential reward functions: Greedy is much better than MAX Greedy = Feasible Thus, Greedy Maximizer is indeed feasibility optimal 24

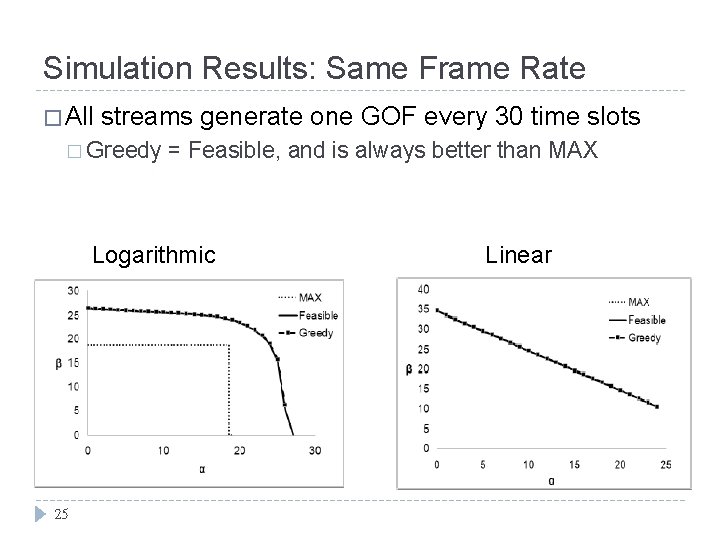
Simulation Results: Same Frame Rate � All streams generate one GOF every 30 time slots � Greedy = Feasible, and is always better than MAX Logarithmic 25 Linear

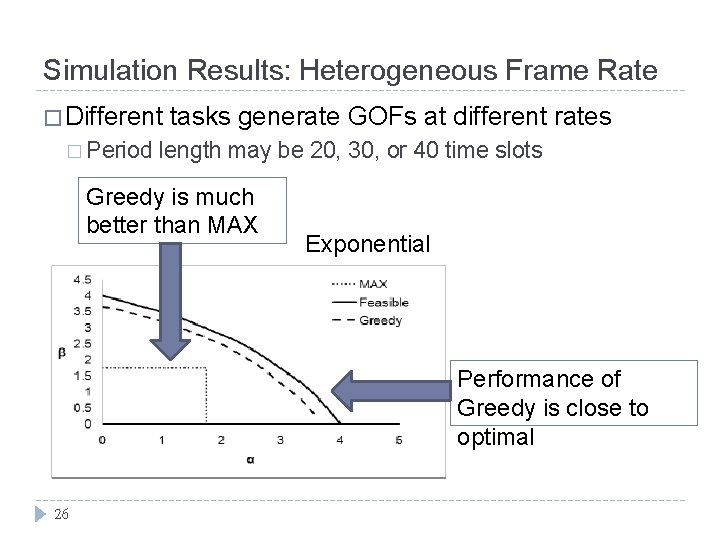
Simulation Results: Heterogeneous Frame Rate � Different � Period tasks generate GOFs at different rates length may be 20, 30, or 40 time slots Greedy is much better than MAX Exponential Performance of Greedy is close to optimal 26

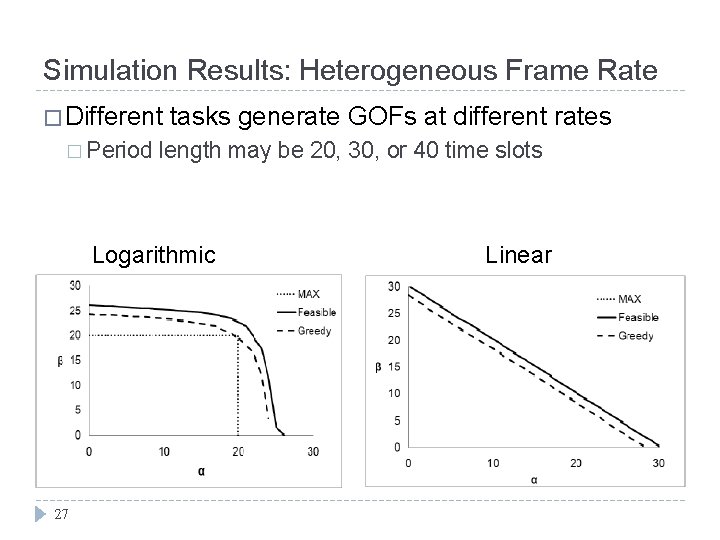
Simulation Results: Heterogeneous Frame Rate � Different � Period tasks generate GOFs at different rates length may be 20, 30, or 40 time slots Logarithmic 27 Linear

Conclusions � We propose a model based on the imprecise computation models that supports per-task reward guarantees � This model can achieve better fairness, and allow fine-grain tradeoff between tasks � Derive a sharp condition for feasibility � Propose an on-line scheduling policy, the Greedy Maximizer � Greedy Maximizer is feasibility optimal when all tasks have the same period length � It is a 2 -approximation policy, otherwise 28