Scheduling in Delay Graphs with Applications to Optical

Scheduling in Delay Graphs with Applications to Optical Networks Isaac Keslassy (Stanford University), Murali Kodialam, T. V. Lakshman, Dimitri Stiliadis (Bell-Labs)

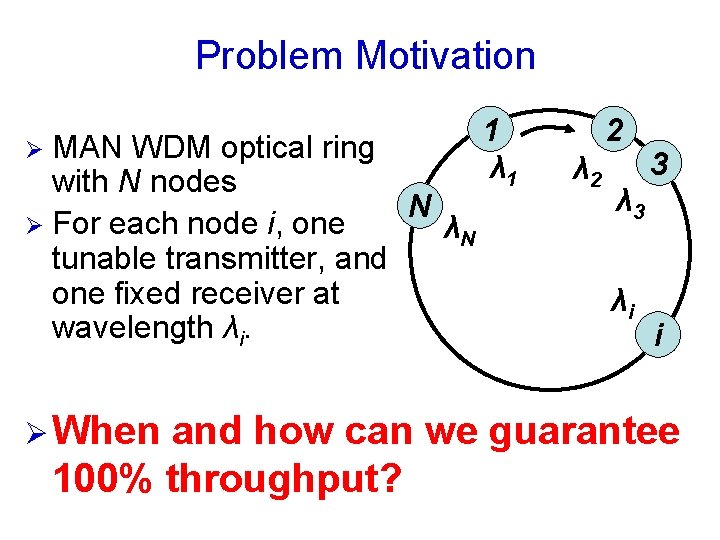
Problem Motivation MAN WDM optical ring with N nodes N Ø For each node i, one λN tunable transmitter, and one fixed receiver at wavelength λi. Ø Ø When 1 λ 1 2 λ 2 3 λi i and how can we guarantee 100% throughput?

Outline Ø Introduction: Scheduling with no Delays Ø Bipartite Delay Graph Ø TSS Algorithm Ø Theorems on Separable Architectures Ø Non-Separable Architectures

Scheduling with no Delays Ø Assume no propagation delays (each packet transmitted is immediately received) Ø A single transmitter and receiver per node => when i sends to j, i cannot send to j’≠j and j cannot receive from i’≠i Ø Slotted time, fixed-size packets

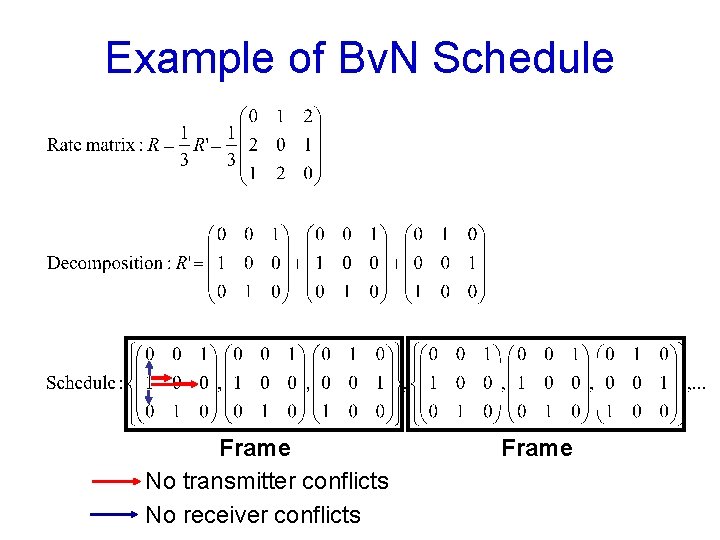
Frame-Based Scheduling Ø Input: Ø Birkhoff-von Neumann (Bv. N) schedule: A frame of F matrices S 1, …, SF such that Ø Ø Ø Arrivals ≤ Services: R’ ≤ S 1 +. . + SF {Si}’s are permutation matrices: any node sends and receives at most one packet per time-slot Known result: decomposition always exists

Example of Bv. N Schedule Frame No transmitter conflicts No receiver conflicts Frame

Neglecting Delays? Ø Propagation delays << time-slot ? Ø Example: MAN WDM ring Ø 30 km ring, 10 Gbps, 1 kb packets Ø Time-slot = 1 kb/(10 Gb/s) = 100 ns Ø Max propagation delay = 30 km/(3. 108 m/s) = 100μs Ø Clearly impossible to neglect delays

Outline Ø Introduction: Scheduling with no Delays Ø Bipartite Delay Graph Ø TSS Algorithm Ø Theorems on Separable Architectures Ø Non-Separable Architectures

Question Ø Question: Can we extend Birkhoff-von Neumann (Bv. N) to general case of WDM mesh with delays Ø Method: Provide simple model for mesh Use model to extend Bv. N 1. 2.

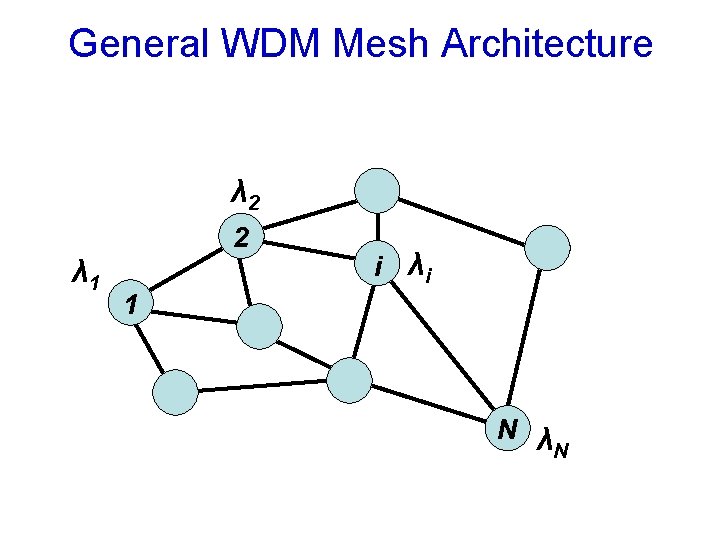
General WDM Mesh Architecture λ 2 2 λ 1 i λi 1 N λ N

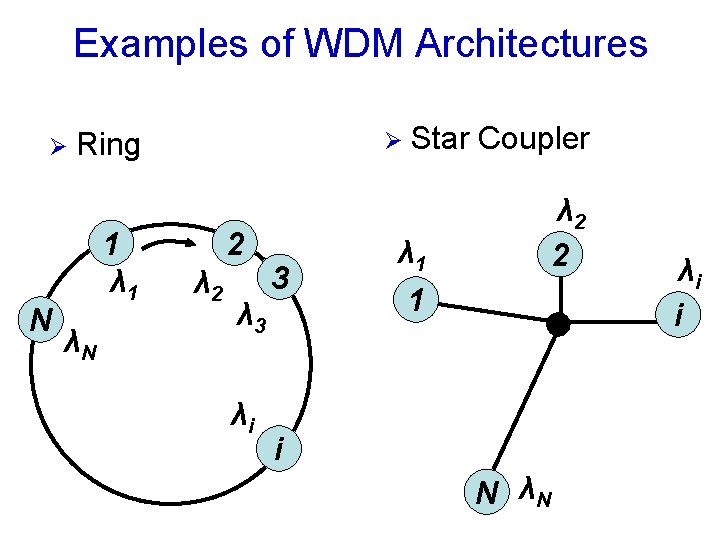
Examples of WDM Architectures Ø N Ring 1 λN Ø 2 λ 2 3 λi Star Coupler λ 2 2 λ 1 1 i N λN λi i

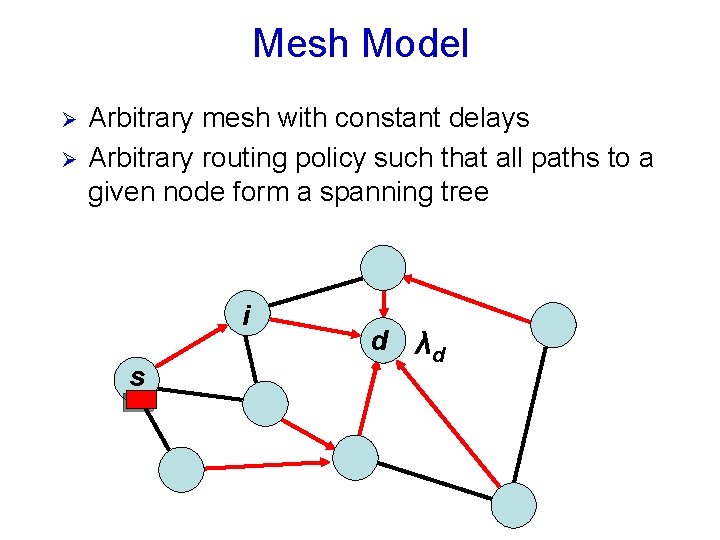
Mesh Model Ø Ø Arbitrary mesh with constant delays Arbitrary routing policy such that all paths to a given node form a spanning tree i s d λd

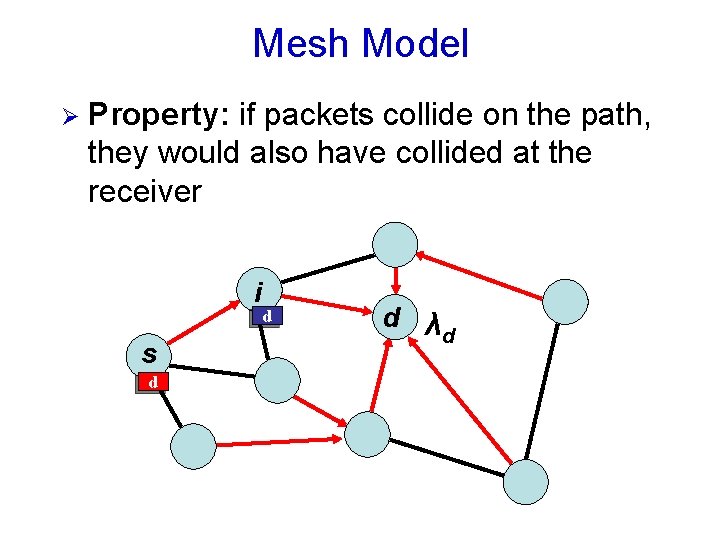
Mesh Model Ø Property: if packets collide on the path, they would also have collided at the receiver i s d d d λ d

Mesh Model Ø Property: if packets collide on the path, they would also have collided at the receiver Ø No collision at receiver no collision on path Ø We need to prevent only two types of collision: Ø At the transmitter Ø At the receiver

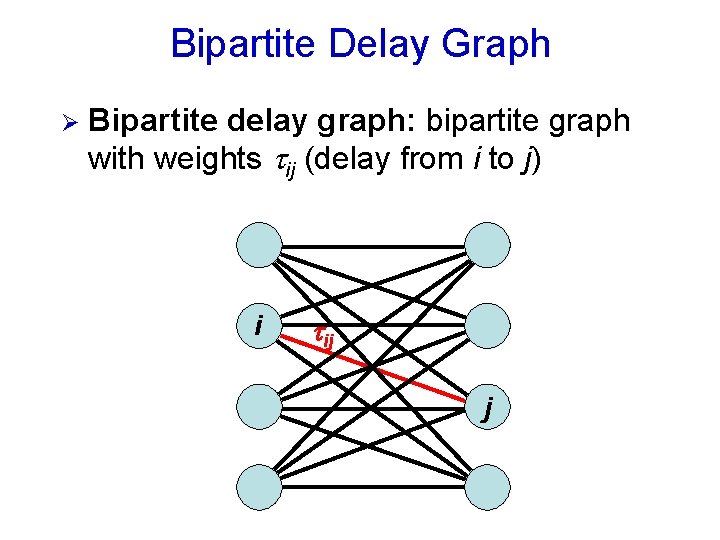
Bipartite Delay Graph Ø Bipartite delay graph: bipartite graph with weights ij (delay from i to j) i ij j

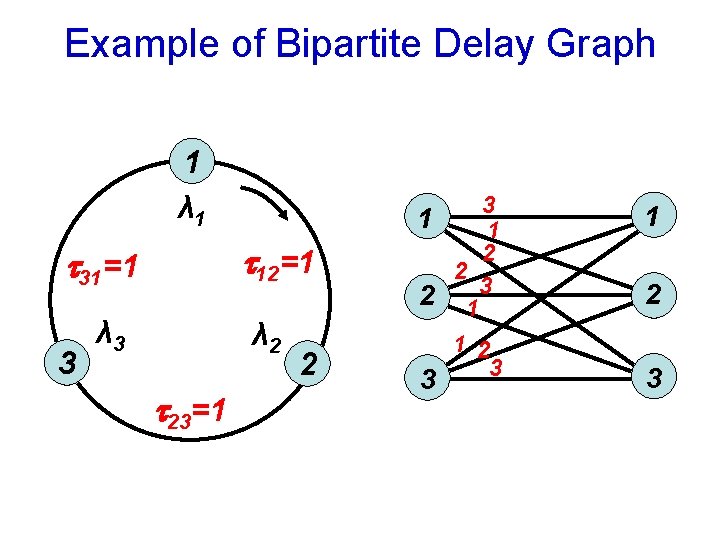
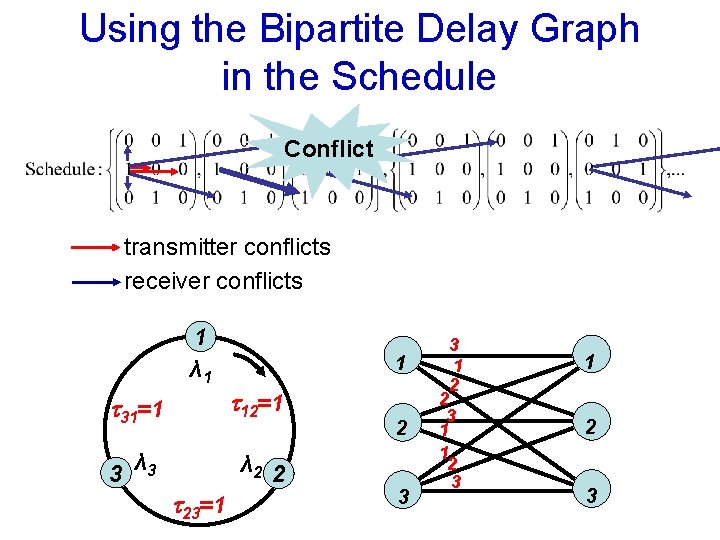
Example of Bipartite Delay Graph 1 λ 1 12=1 31=1 3 λ 2 23=1 3 1 2 2 2 13 1 2 3

Using the Bipartite Delay Graph in the Schedule Conflict transmitter conflicts receiver conflicts 1 λ 1 1 31=1 12=1 3 λ 2 2 23=1 2 3 3 1 2 2 3 1 1 2 3

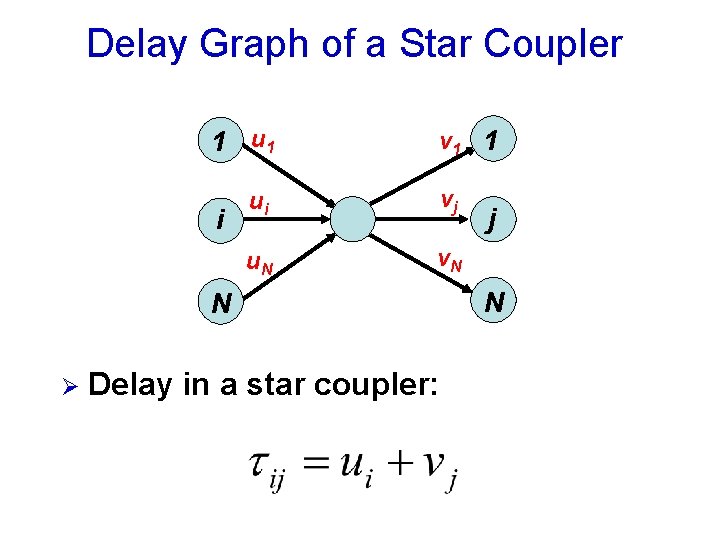
Delay Graph of a Star Coupler 1 u 1 i v 1 1 ui vj u. N v. N N Ø Delay in a star coupler: j N

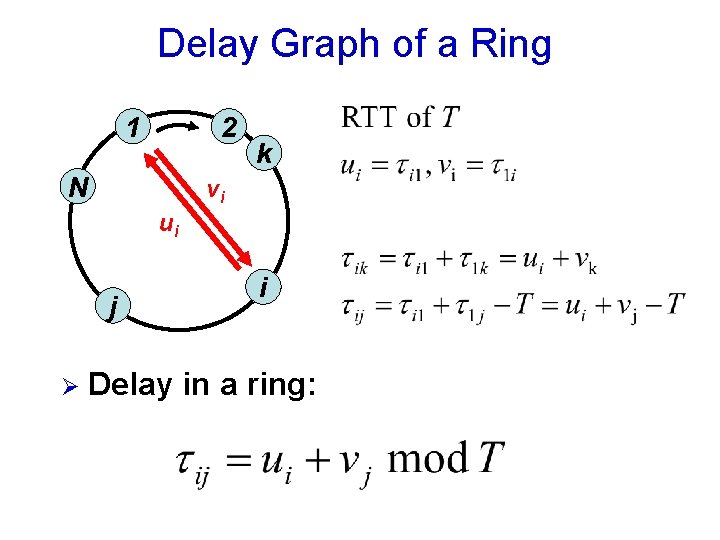
Delay Graph of a Ring 1 2 N k vi ui j Ø i Delay in a ring:

Outline Ø Introduction: Scheduling with no Delays Ø Bipartite Delay Graph Ø TSS Algorithm Ø Theorems on Separable Architectures Ø Non-Separable Architectures

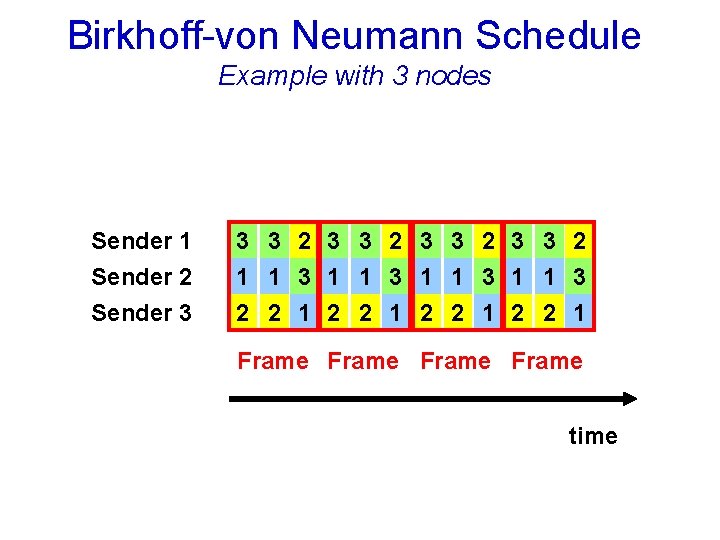
Birkhoff-von Neumann Schedule Example with 3 nodes Sender 1 3 3 2 Sender 2 Sender 3 1 1 3 2 2 1 Frame time

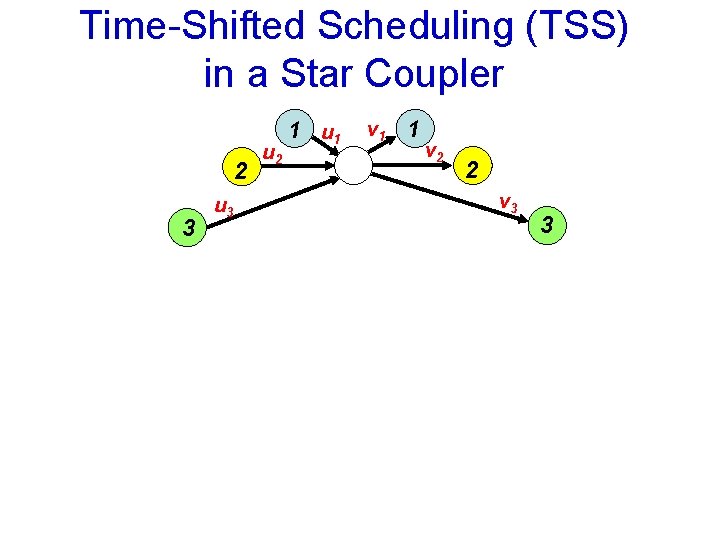
Time-Shifted Scheduling (TSS) in a Star Coupler 2 3 u 2 1 u 1 v 1 1 v 2 2 v 3 3

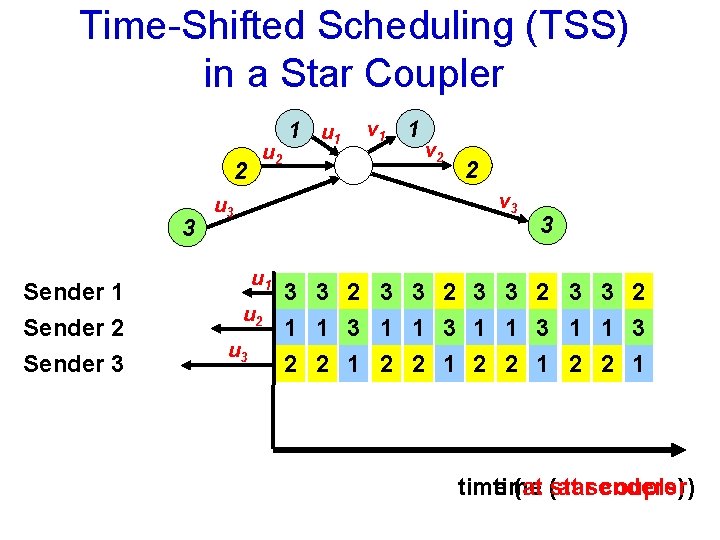
Time-Shifted Scheduling (TSS) in a Star Coupler u 2 2 3 Sender 1 Sender 2 Sender 3 1 u 1 v 1 1 v 2 2 v 3 u 1 u 2 u 3 3 2 3 3 2 1 1 3 2 2 1 time (at starsenders) coupler)

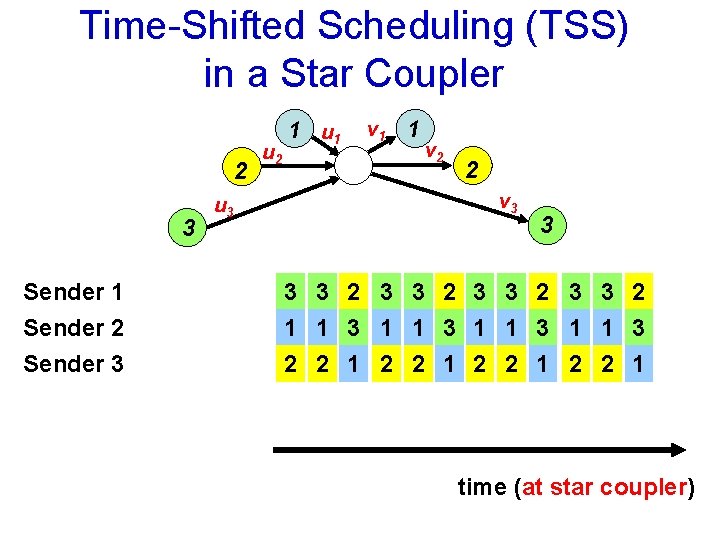
Time-Shifted Scheduling (TSS) in a Star Coupler 2 3 Sender 1 Sender 2 Sender 3 u 2 1 u 1 v 1 1 v 2 2 v 3 3 2 3 3 2 1 1 3 2 2 1 time (at star coupler)

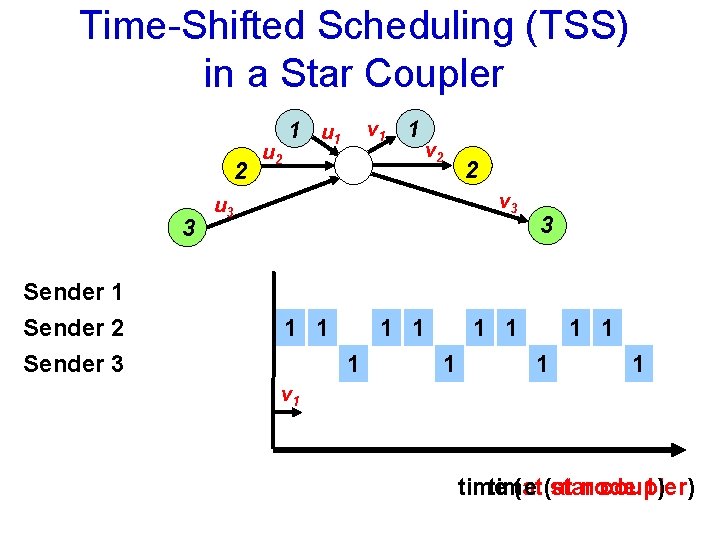
Time-Shifted Scheduling (TSS) in a Star Coupler 2 3 Sender 1 Sender 2 Sender 3 u 2 1 u 1 v 1 1 v 2 2 v 3 u 3 1 1 1 1 v 1 time (at(at star node coupler) 1)

TSS in a Star Coupler and in a Ring Ø In a star coupler, TSS works: Ø In a ring with RTT T, and a schedule of frame length F=T, TSS also works (shifting time by T doesn’t matter): and the schedule is modulo F=T.

Definitions (more general setting) Ø Separable architecture: Ø T-Separable architecture: ØA separable architecture is T-separable for all T Ø F-rate matrix: Rate matrix for which (optimal) Bv. N decomposition has frame length F

Properties Ø Property 1: Using the TSS algorithm, an F -separable architecture can schedule any F-rate matrix. Ø Example: Ø ring of RTT F Property 2: Using the TSS algorithm, a separable architecture can schedule any rate matrix. Ø Example: star coupler

Outline Ø Introduction: Scheduling with no Delays Ø Bipartite Delay Graph Ø TSS Algorithm Ø Theorems on Separable Architectures Ø Non-Separable Architectures

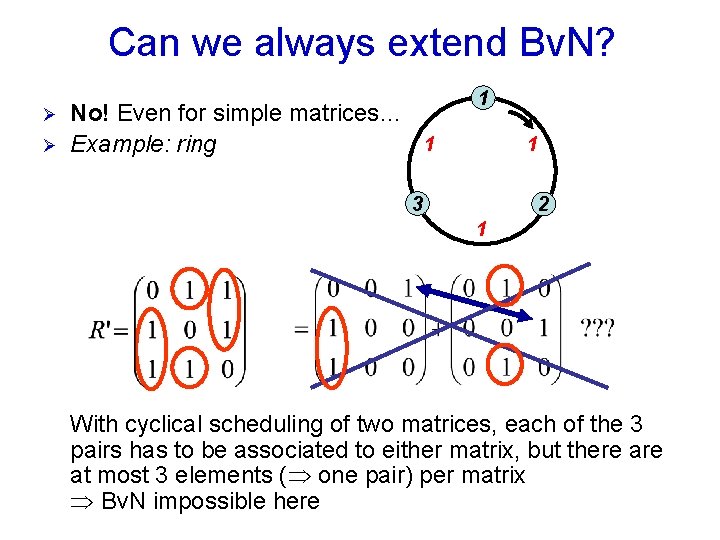
Can we always extend Bv. N? Ø Ø No! Even for simple matrices… 1 Example: ring 1 1 3 2 1 With cyclical scheduling of two matrices, each of the 3 pairs has to be associated to either matrix, but there at most 3 elements ( one pair) per matrix Bv. N impossible here

Theorems (Necessity and Sufficiency) Ø Theorem 1: An architecture can schedule any Frate matrix iff the architecture is F-separable. Ø Ø Theorem 2: An architecture can schedule any rate matrix iff the architecture is separable. Ø Ø Proof: if not F-separable, exhibit counter-example Proof: needs to be F-separable for all F Corollary (Negative result): Guaranteed framebased scheduling cannot be achieved in nonseparable architectures.

Outline Ø Introduction: Scheduling with no Delays Ø Bipartite Delay Graph Ø TSS Algorithm Ø Theorems on Separable Architectures Ø Non-Separable Architectures

Non-Separable Delay Graphs Guaranteed schedule in non-separable architecture? need to make it separable Ø Assume we can add delay lines ij between nodes. Ø How to minimize the sum of these delay lines? Ø

Non-Separable Delay Graphs Ø Dual formulation of Maximum Weight Matching Problem in Bipartite Delay Graph Ø Separable architecture: all matches are MWM Non-separable architecture: solving MWM gives minimum amount of additional delay lines Ø

Summary Ø The bipartite delay graph can model any mesh architecture Ø An architecture can schedule any F-rate matrix iff it is F-separable (e. g. ring of RTT=F) Ø An architecture can schedule any rate matrix iff it is separable (e. g. star coupler) Ø Non-separable architectures can schedule any rate matrix at minimum cost by adding delay lines and using maximum weight matching

Thank you.