Scheduling Algorithm and Analysis ESP Fall 2014 Computer

Scheduling Algorithm and Analysis (ESP – Fall 2014) Computer Science & Engineering Department Arizona State University Tempe, AZ 85287 Dr. Yann-Hang Lee yhlee@asu. edu (480) 727 -7507 Real-time Systems Lab, Computer Science and Engineering, ASU

Task Scheduling q Schedule: to determine which task is assigned to a processor at any time v order of execution v meet deadlines, fast response time, utilize resource effectively q Need an algorithm to generate a schedule v optimal scheduling algorithm: always find a feasible schedule if and only if a feasible schedule exists q Scheduler or dispatcher: the mechanism to implement a schedule q Misconcept: v RTOS will schedule tasks to meet task deadlines v A good schedule will reduce CPU load Real-time Systems Lab, Computer Science and Engineering, ASU 1

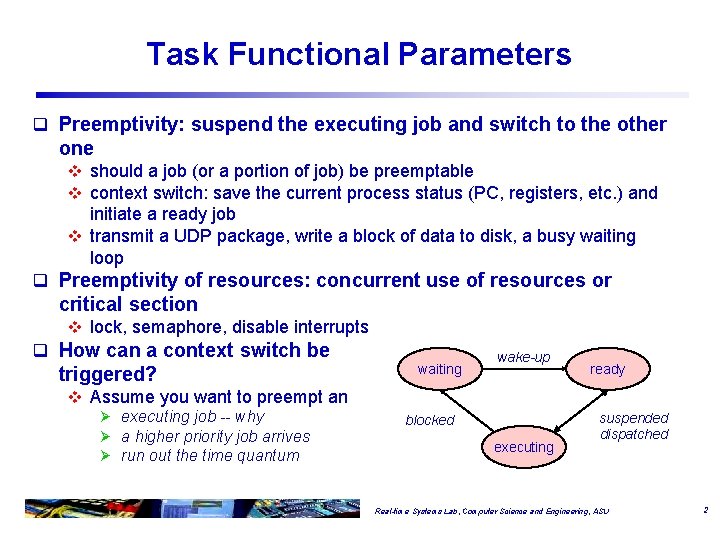
Task Functional Parameters q Preemptivity: suspend the executing job and switch to the other one v should a job (or a portion of job) be preemptable v context switch: save the current process status (PC, registers, etc. ) and initiate a ready job v transmit a UDP package, write a block of data to disk, a busy waiting loop q Preemptivity of resources: concurrent use of resources or critical section v lock, semaphore, disable interrupts q How can a context switch be triggered? v Assume you want to preempt an Ø executing job -- why Ø a higher priority job arrives Ø run out the time quantum waiting wake-up blocked executing ready suspended dispatched Real-time Systems Lab, Computer Science and Engineering, ASU 2

Event- and Time-Triggered Systems q Time-triggered control system v All activities are carried out at certain points in time know a priori at design time (based on a globally synchronized time base) Ø Transmission of messages Ø Task execution Ø Monitoring of external states v All nodes have a common notion of time q Event-triggered control system v All activities are carried out in response to events external to the system Ø Reception of a message Ø Termination of a task Ø External interrup Real-time Systems Lab, Computer Science and Engineering, ASU 3

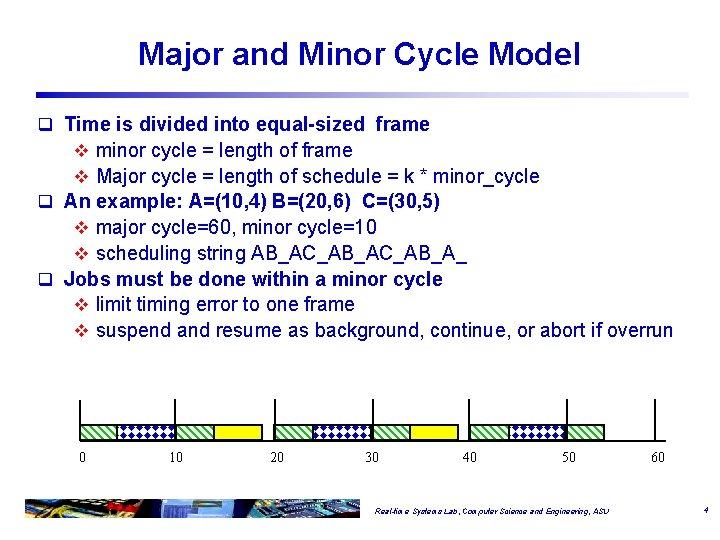
Major and Minor Cycle Model q Time is divided into equal-sized frame v minor cycle = length of frame v Major cycle = length of schedule = k * minor_cycle q An example: A=(10, 4) B=(20, 6) C=(30, 5) v major cycle=60, minor cycle=10 v scheduling string AB_AC_AB_A_ q Jobs must be done within a minor cycle v limit timing error to one frame v suspend and resume as background, continue, or abort if overrun 0 10 20 30 40 50 Real-time Systems Lab, Computer Science and Engineering, ASU 60 4

An Example q A 1 must be done at least every 10 ms, and takes 1 ms q A 2 must be completed with 5 ms when E occurs and takes 2 ms q E must be detected by polling and is detectable for at least 0. 5 ms 0. 5 ms q E would not occur twice within 50 ms q polling of E takes 0 overhead Real-time Systems Lab, Computer Science and Engineering, ASU 5

Major/Minor Cyclic Scheduling q There should be a periodic polling action for E v Assume a timer of 0. 5 ms to activate polling operation and no polling overhead q Should be an interval of 2 ms to execute A 2 for an arbitrary 5 ms interval v May detect E in the first frame and execute A 2 in the second frame period=2. 5 ms v A 2 takes 2 ms if E, otherwise is 0 WCET=2 ms q Should be an interval of 1 ms to execute A 1 for an arbitrary 10 ms interval v Period= 10 ms, WCET= 1 ms v Since 2 ms + 1 ms > 2. 5 ms, we will divide A 1 into two parts of 0. 5 ms A 2 A 1_1 A 2 A 1_2 A 2 A 2 Real-time Systems Lab, Computer Science and Engineering, ASU 6

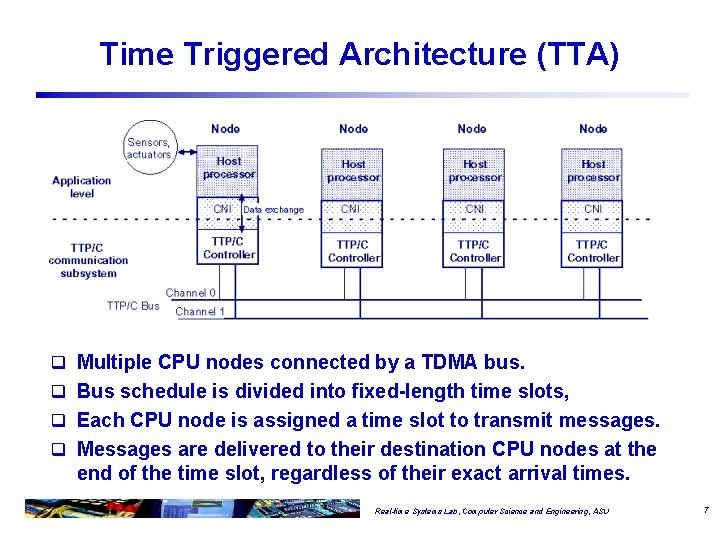
Time Triggered Architecture (TTA) q Multiple CPU nodes connected by a TDMA bus. q Bus schedule is divided into fixed-length time slots, q Each CPU node is assigned a time slot to transmit messages. q Messages are delivered to their destination CPU nodes at the end of the time slot, regardless of their exact arrival times. Real-time Systems Lab, Computer Science and Engineering, ASU 7

Summary of Cyclic Schedule q Pros v simple, table-driven, easy to validate (knows what is doing at any moment) v fit well for harmonic periods and small system variations v static schedule deterministic, static resource allocation, no preemption v small jitter, no scheduling anomalies q Cons v v v difficult to change (need to re-schedule all tasks) fixed released times for the set of tasks difficult to deal with dependencies schedule algorithm may get complex (NP-hard) doesn’t support aperiodic tasks efficiently Processes with sizeable computation times. Real-time Systems Lab, Computer Science and Engineering, ASU 8

Priority-Driven Scheduling of Periodic Tasks q Why priority-driven scheduling v use priority to represent urgency v easy implementation of scheduler (compare priorities and dispatch tasks) v tasks can be added or removed easily v no direct control of execution instance q How can we analyze the schedulability if we don’t know when a task is to be executed q Let’s begin a deterministic case in one processor v independent periodic tasks v deadline = period v preemptable v no overhead for context switch Real-time Systems Lab, Computer Science and Engineering, ASU 9

Priority-Driven Schedules q Assign priority when jobs arrive v static -- all jobs of a task have a fixed priority v dynamic -- different priorities to individual tasks of a task v relative priorities don’t change while jobs are waiting q Static priority schedules v Rate-monotonic -- the smaller a task period, the higher its priority v Deadline-monotonic – if deadline period, the smaller a task’s deadline (relative), the higher its priority q Dynamic priority schedules v EDF -- earliest deadline (absolute) first q Schedulable utilization: v a scheduling algorithm can feasibly schedule any sets of priority tasks if the total utilization is equal to or less than the schedulable utilization of the algorithm Real-time Systems Lab, Computer Science and Engineering, ASU 10

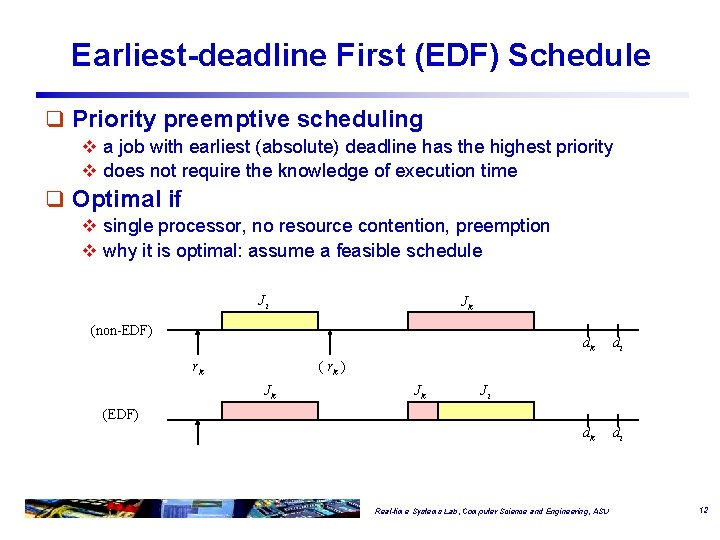
Earliest-deadline First (EDF) Schedule q Priority preemptive scheduling v a job with earliest (absolute) deadline has the highest priority v does not require the knowledge of execution time q Optimal if single processor, no resource contention, preemption q Scheduling anomaly if non-preemptive --- the schedule fails after we reduce job execution times D 1 D 2 D 3 T 1 T 2 T 3 Missed deadline ( all jobs meet their deadline under EDF after increasing e 1 ) Real-time Systems Lab, Computer Science and Engineering, ASU 11

Earliest-deadline First (EDF) Schedule q Priority preemptive scheduling v a job with earliest (absolute) deadline has the highest priority v does not require the knowledge of execution time q Optimal if v single processor, no resource contention, preemption v why it is optimal: assume a feasible schedule Ji Jk (non-EDF) rk dk di ( rk ) Jk Jk Ji (EDF) Real-time Systems Lab, Computer Science and Engineering, ASU 12

EDF Schedule q A optimal algorithm under single processor and preemptable tasks q How do we know a set of periodic tasks are schedulable under EDF ? q If we know the schedulable utilization SU of EDF, then any sets of tasks are schedulable when U SU q Theorem: A set of n periodic tasks can be scheduled by EDF iff q This schedulability utilization is no long true if deadline < period. Real-time Systems Lab, Computer Science and Engineering, ASU 13

Example of EDF Schedule q A digital robot with EDF schedule v control loop: ec 8 ms at 100 Hz v BIST: eb 50 ms v given v BIST can be done every 250 ms q Add a telemetry task to send and receive messages with et 15 ms v if BIST is done every 1000 ms v given v the telemetry task can have a relative deadline of 100 ms v sending or receiving must be separated at least 100 ms Real-time Systems Lab, Computer Science and Engineering, ASU 14

Rate-Monotonic Scheduling Algorithm q A base case: no additional overhead, simple periodic tasks with pi =Di q Assign priorities according their periods v Ti has a higher priority that Tk if i < k ( pi < pk ) v Is RM optimal? if there is a feasible fixed-priority schedule, then RM is feasible v How do we know RM is feasible schedulability test q Results: v RM is optimal if pi Di v sufficient condition utilization test v a complete test what is the worst response time given all possible arrivals and preemptions Real-time Systems Lab, Computer Science and Engineering, ASU 15

Critical Instant q Critical instant of Ti: a job of Ti arriving at the instant has a maximum response time q If we can find the critical instant of Ti, then v check whether all jobs of Ti meet their deadlines v let’s increase ei until the maximum response time = Di v schedulable utilization q In-phase instant is critical: all higher priority tasks are released at the same instant (assume all jobs are completed before the next job in the tasme task is released. ) v which T 2 has the maximum response time T 1 T 2 T 1, T 2 T 1 Real-time Systems Lab, Computer Science and Engineering, ASU 16

Schedulability: UB Test q Utilization bound (UB) test: a set of n independent periodic tasks scheduled by the rate monotonic algorithm will always meet its deadlines, for all task phasings, if U(1) = 1. 0 U(2) = 0. 828 U(3) = 0. 779 U(4) = 0. 756 U(5) = 0. 743 U(6) = 0. 734 U(7) = 0. 728 U(8) = 0. 724 U(9) = 0. 720 q For harmonic task sets, the utilization bound is U(n)=1. 00 for all n. Real-time Systems Lab, Computer Science and Engineering, ASU 17

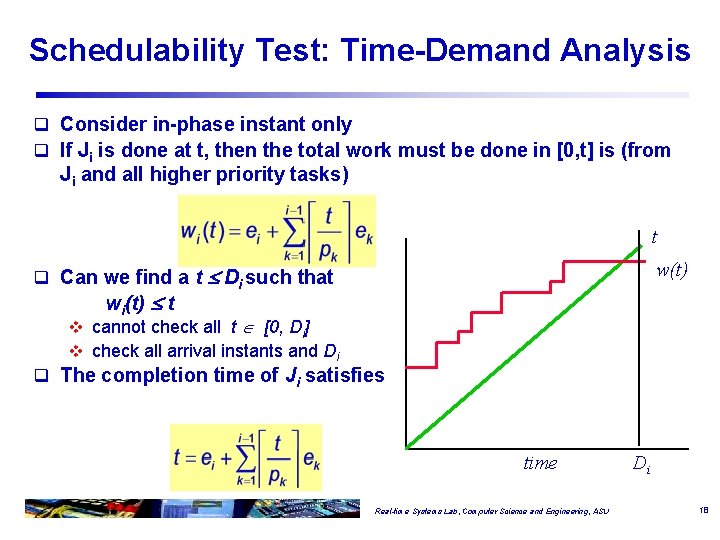
Schedulability Test: Time-Demand Analysis q Consider in-phase instant only q If Ji is done at t, then the total work must be done in [0, t] is (from Ji and all higher priority tasks) t w(t) q Can we find a t Di such that wi(t) t v cannot check all t [0, Di] v check all arrival instants and Di q The completion time of Ji satisfies time Real-time Systems Lab, Computer Science and Engineering, ASU Di 18

Schedulability: RT Test q Theorem: for a set of independent, periodic tasks, if each task meets its first deadline, with worst-case task phasing, the deadline will always be met. q Response Time (RT) test: v let an = response time of task i. iterative formula: an may be computed by the following v Test terminates when an+1 = an v Task i is schedulable if its response time is before its deadline: an ≤ Ti Real-time Systems Lab, Computer Science and Engineering, ASU 19

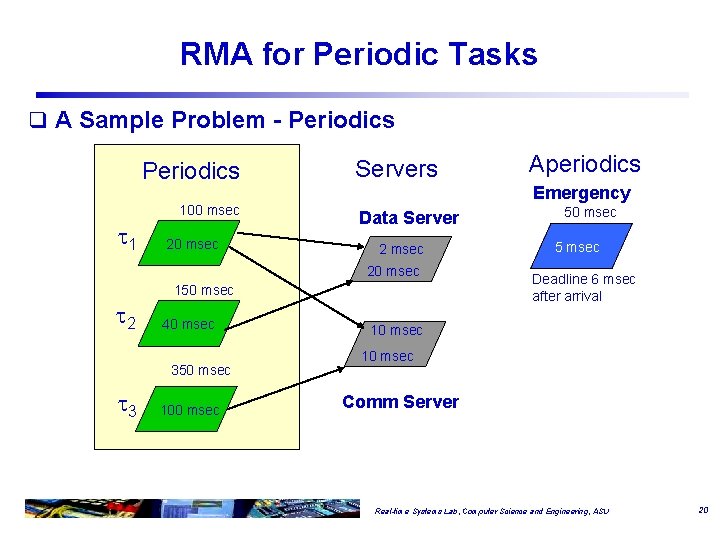
RMA for Periodic Tasks q A Sample Problem - Periodics 100 msec 1 20 msec Servers Emergency Data Server 2 msec 20 msec 150 msec 2 40 msec 350 msec 3 100 msec Aperiodics 50 msec 5 msec Deadline 6 msec after arrival 10 msec Comm Server Real-time Systems Lab, Computer Science and Engineering, ASU 20

Sample Problem: UB Test e p U Task 1 20 100 0. 200 Task 2 40 150 0. 267 Task 3 100 350 0. 286 q Total utilization is . 200 +. 267 +. 286 =. 753 < U(3) =. 779 q The periodic tasks in the sample problem are schedulable according to the UB test. Real-time Systems Lab, Computer Science and Engineering, ASU 21

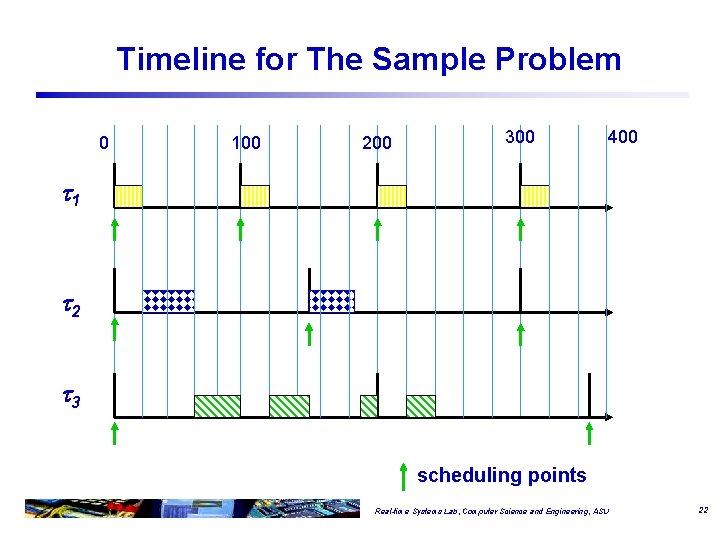
Timeline for The Sample Problem 0 100 200 300 400 1 2 3 scheduling points Real-time Systems Lab, Computer Science and Engineering, ASU 22

Example: Applying RT Test (1) q Taking the sample problem, we increase the compute time of ז 1 from 20 to 40; is the task set still schedulable? q Utilization for the first task : 40/100=0. 4 < U(1) q Utilization of first two tasks: 0. 667 < U(2) = 0. 828 v First two tasks are schedulable by UB test q Utilization of all three tasks: 0. 953 > U(3) = 0. 779 v UB test is inconclusive v Need to apply RT test Real-time Systems Lab, Computer Science and Engineering, ASU 23

Example: Applying RT Test (2) q Use RT test to determine if ז 3 meets its first deadline: i=3 Real-time Systems Lab, Computer Science and Engineering, ASU 24

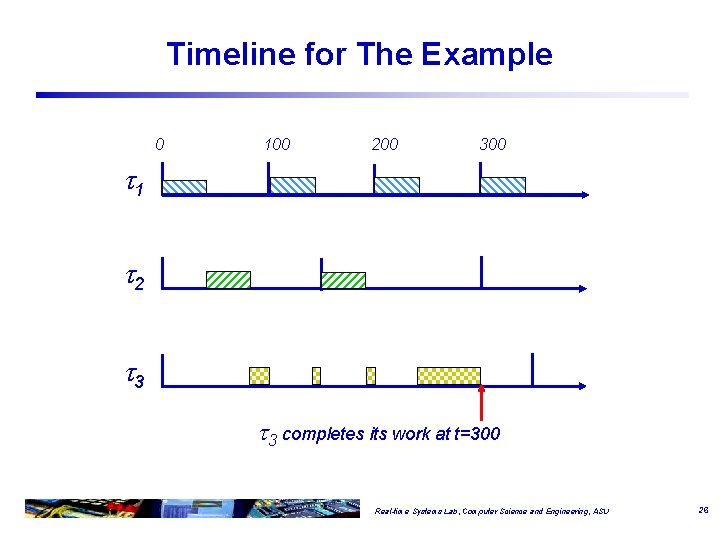
Example: Applying RT Test (3) a 3 = a 2 = 300 Done! q Task is schedulable using RT test. v a 3 = 300 < p 3 = 350 Real-time Systems Lab, Computer Science and Engineering, ASU 25

Timeline for The Example 0 100 200 300 1 2 3 3 completes its work at t=300 Real-time Systems Lab, Computer Science and Engineering, ASU 26

Summary q UB test is simple but conservative q RT test is more exact but also more complicated q To this point, UB and RT tests share the same limitations: v All tasks run on a single processor v All tasks are periodic and noninteracting v Deadlines are always at the end of the period v There are no interrupts v Rate monotonic priorities are assigned v There is zero context switch overhead v Tasks do not suspend themselves Real-time Systems Lab, Computer Science and Engineering, ASU 27

Modeling Task Switching Real-time Systems Lab, Computer Science and Engineering, ASU 28

Schedulability with Interrupts q Interrupt processing can be inconsistent with rate monotonic priority assignment. v interrupt handler executes with high priority despite its period v interrupt processing may delay execution of tasks with shorter periods q Effects of interrupt processing must be taken into account in schedulability model. q Question is: how to do that? Real-time Systems Lab, Computer Science and Engineering, ASU 29

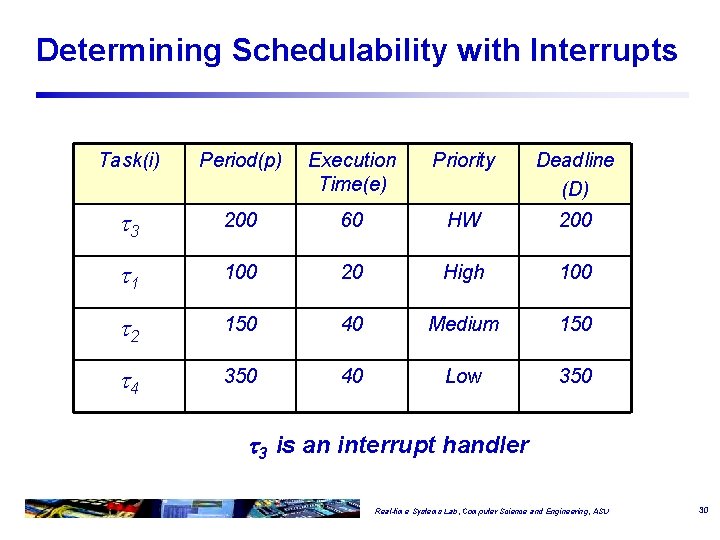
Determining Schedulability with Interrupts Task(i) Period(p) Execution Time(e) Priority Deadline (D) 3 200 60 HW 200 1 100 20 High 100 2 150 40 Medium 150 4 350 40 Low 350 3 is an interrupt handler Real-time Systems Lab, Computer Science and Engineering, ASU 30

UB Test with Interrupt Priority q Test is applied to each task. q Determine effective utilization (fi) of each task i using Preemption form the tasks that can hit more than once (with period less that Di) Execution of a task under test Preemption from tasks That can hit only once (with period greater than Di ) q Compare effective utilization against bound, U(n). n = num(Hn) + 1 num(Hn) = the number of tasks in the set Hn Real-time Systems Lab, Computer Science and Engineering, ASU 31

UB Test with Interrupt Priority: 3 q For 3, no tasks have a higher priority: H = Hn =H 1 = { }. q Note that utilization bound is U(1): num(Hn) = 0. Plugging in numbers: Real-time Systems Lab, Computer Science and Engineering, ASU 32

UB Test with Interrupt Priority: 1 q For 1, 3 has a higher priority: H = { 3}; Hn = {}; H 1 = { 3}. q Note that utilization bound is U(1): num(Hn) = 0. Plugging in the numbers: Real-time Systems Lab, Computer Science and Engineering, ASU 33

UB Test with Interrupt Priority: 2 q For 2 : H={ 1, 3}; Hn={ 1 }; H 1={ 3 }; q Note that utilization bound is U(2): num(Hn) = 1. Plugging in the numbers: Real-time Systems Lab, Computer Science and Engineering, ASU 34

UB Test with Interrupt Priority: q For 4 : H={ 1, 2, 3}; Hn={ 1 , 2, 3 }; H 1={}; q Note that utilization bound is U(4): num(Hn) = 3. Plugging in the numbers: Real-time Systems Lab, Computer Science and Engineering, ASU 35

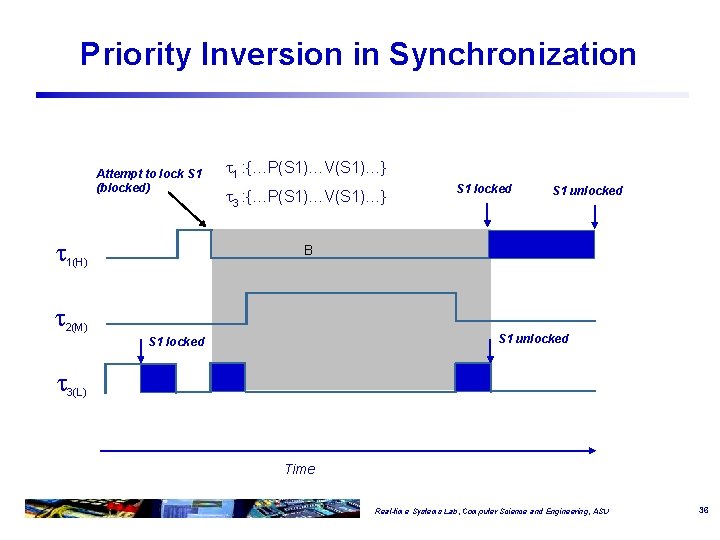
Priority Inversion in Synchronization Attempt to lock S 1 (blocked) 1(H) 1 : {…P(S 1)…V(S 1)…} 3 : {…P(S 1)…V(S 1)…} S 1 locked S 1 unlocked B 2(M) S 1 unlocked S 1 locked 3(L) Time Real-time Systems Lab, Computer Science and Engineering, ASU 36

Priority Inversion q Delay to a task’s execution caused by interference from lower priority tasks is known as priority inversion q Preemption is normal, but priority inversion should be avoided q Priority inversion is modeled by blocking time q Identifying and evaluating the effect of sources of priority inversion is important in schedulability analysis q Sources of priority Inversion v Synchronization and mutual exclusion v Non-preemtable regions of code v FIFO (first-in-first-out) queues Real-time Systems Lab, Computer Science and Engineering, ASU 37

Accounting for Priority Inversion q Recall that task schedulability is affected by v preemption: two types of preemption Ø can occur several times period Ø can occur once period v execution: once period v blocking: at most once period for each source q The schedulability formulas are modified to add a “blocking” or “priority inversion” term to account for inversion effects Real-time Systems Lab, Computer Science and Engineering, ASU 38

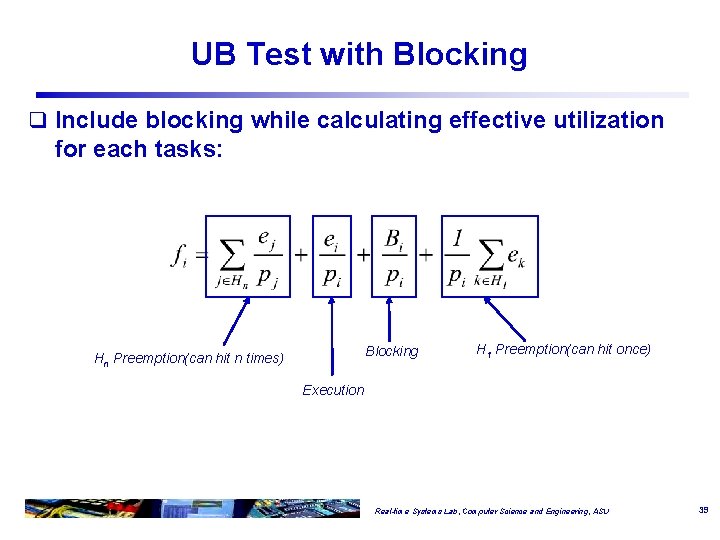
UB Test with Blocking q Include blocking while calculating effective utilization for each tasks: Blocking Hn Preemption(can hit n times) H 1 Preemption(can hit once) Execution Real-time Systems Lab, Computer Science and Engineering, ASU 39

RT Test with Blocking q Blocking is also included in the RT test q Perform test as before, including blocking effect Real-time Systems Lab, Computer Science and Engineering, ASU 40

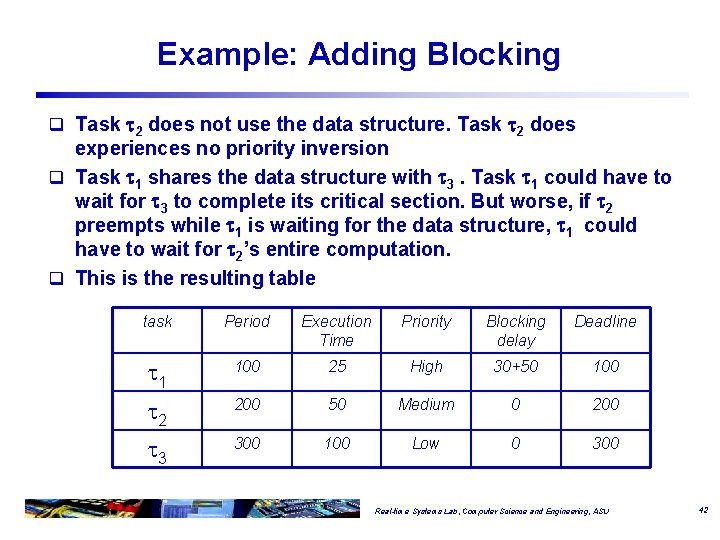
Example: Considering Blocking q Consider the following example Periodic tasks 1 2 3 100 msec 25 msec 200 msec Data Structure 10 msec 30 msec 50 msec 300 msec 100 msec What is the worst case blocking effect (priority inversion) experienced by each task ? Real-time Systems Lab, Computer Science and Engineering, ASU 41

Example: Adding Blocking q Task 2 does not use the data structure. Task 2 does experiences no priority inversion q Task 1 shares the data structure with 3. Task 1 could have to wait for 3 to complete its critical section. But worse, if 2 preempts while 1 is waiting for the data structure, 1 could have to wait for 2’s entire computation. q This is the resulting table task Period Execution Time Priority Blocking delay Deadline 1 100 25 High 30+50 100 2 200 50 Medium 0 200 3 300 100 Low 0 300 Real-time Systems Lab, Computer Science and Engineering, ASU 42

UB Test for Example q Recall UB test with blocking: Not schedulable with additional RT test, 3 is shown to be schedulable Real-time Systems Lab, Computer Science and Engineering, ASU 43

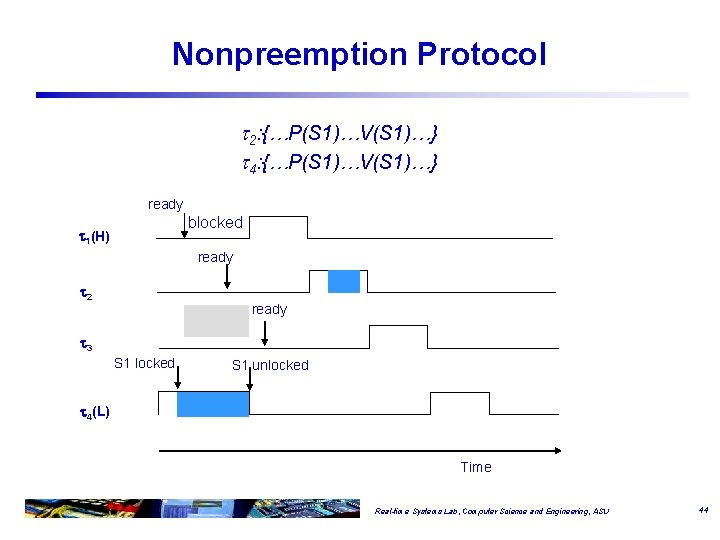
Nonpreemption Protocol 2: {…P(S 1)…V(S 1)…} 4: {…P(S 1)…V(S 1)…} ready blocked 1(H) ready 2 ready 3 S 1 locked S 1 unlocked 4(L) Time Real-time Systems Lab, Computer Science and Engineering, ASU 44

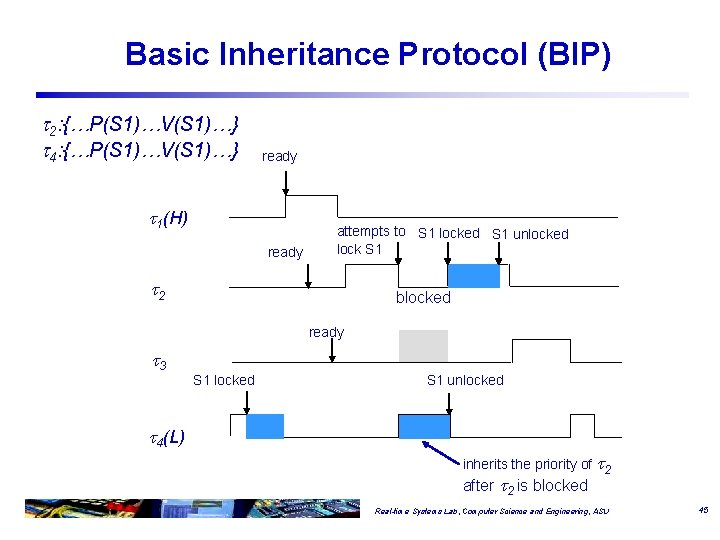
Basic Inheritance Protocol (BIP) 2: {…P(S 1)…V(S 1)…} 4: {…P(S 1)…V(S 1)…} ready 1(H) ready attempts to S 1 locked S 1 unlocked lock S 1 2 blocked ready 3 S 1 locked S 1 unlocked 4(L) inherits the priority of 2 after 2 is blocked Real-time Systems Lab, Computer Science and Engineering, ASU 45

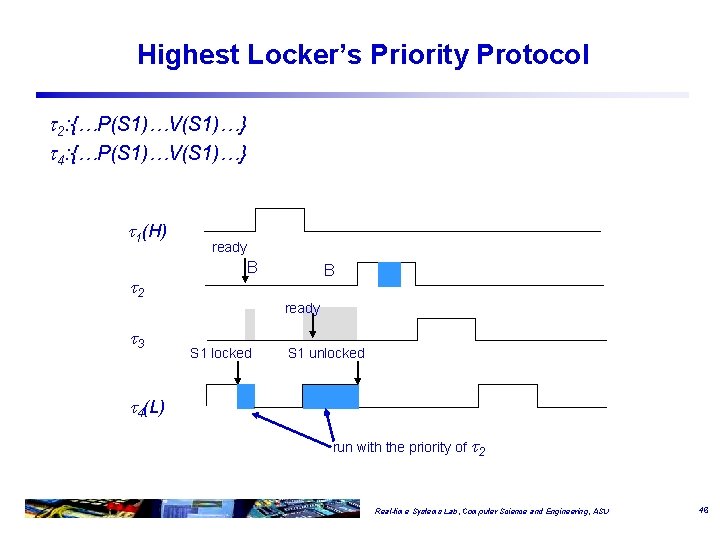
Highest Locker’s Priority Protocol 2: {…P(S 1)…V(S 1)…} 4: {…P(S 1)…V(S 1)…} 1(H) 2 ready B B ready 3 S 1 locked S 1 unlocked 4(L) run with the priority of 2 Real-time Systems Lab, Computer Science and Engineering, ASU 46

Summary of Synchronization Protocols Only if tasks do not suspend within critical sections 2 PCP is not affected if tasks suspend within critical sections. 1 Real-time Systems Lab, Computer Science and Engineering, ASU 47

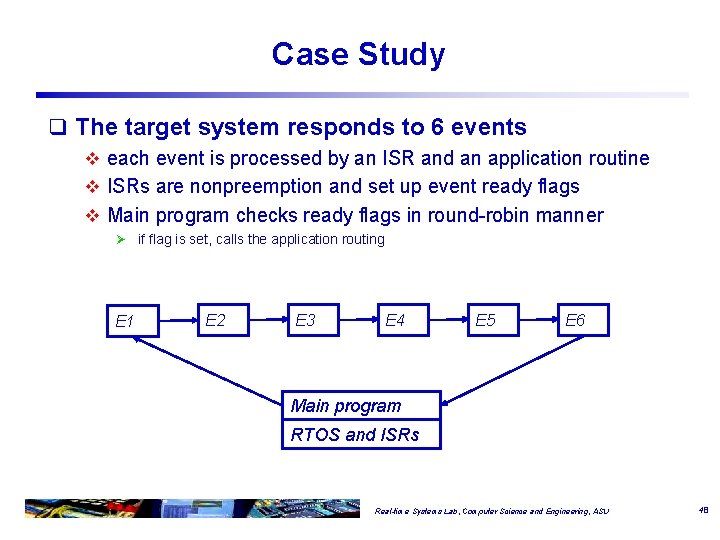
Case Study q The target system responds to 6 events v each event is processed by an ISR and an application routine v ISRs are nonpreemption and set up event ready flags v Main program checks ready flags in round-robin manner Ø if flag is set, calls the application routing E 1 E 2 E 3 E 4 E 5 E 6 Main program RTOS and ISRs Real-time Systems Lab, Computer Science and Engineering, ASU 48

Scheduling Discipline wait for signals Real-time Systems Lab, Computer Science and Engineering, ASU 49

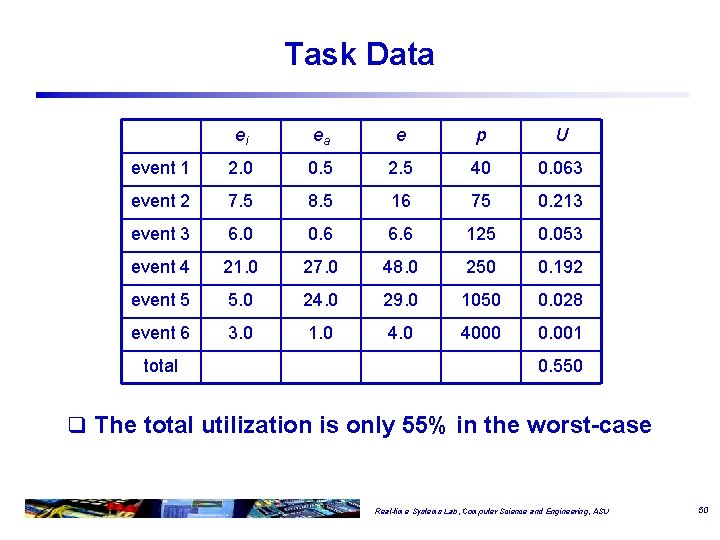
Task Data ei ea e p U event 1 2. 0 0. 5 2. 5 40 0. 063 event 2 7. 5 8. 5 16 75 0. 213 event 3 6. 0 0. 6 6. 6 125 0. 053 event 4 21. 0 27. 0 48. 0 250 0. 192 event 5 5. 0 24. 0 29. 0 1050 0. 028 event 6 3. 0 1. 0 4000 0. 001 total 0. 550 q The total utilization is only 55% in the worst-case Real-time Systems Lab, Computer Science and Engineering, ASU 50

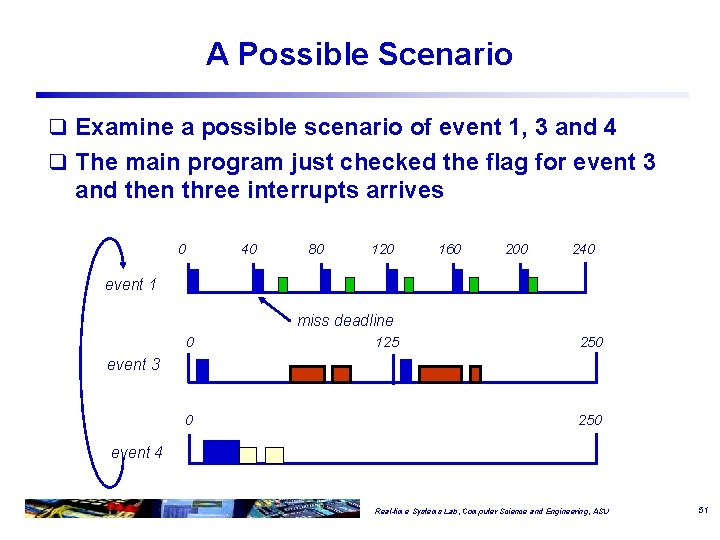
A Possible Scenario q Examine a possible scenario of event 1, 3 and 4 q The main program just checked the flag for event 3 and then three interrupts arrives 0 40 80 120 160 200 240 event 1 miss deadline 0 125 250 event 3 0 250 event 4 Real-time Systems Lab, Computer Science and Engineering, ASU 51

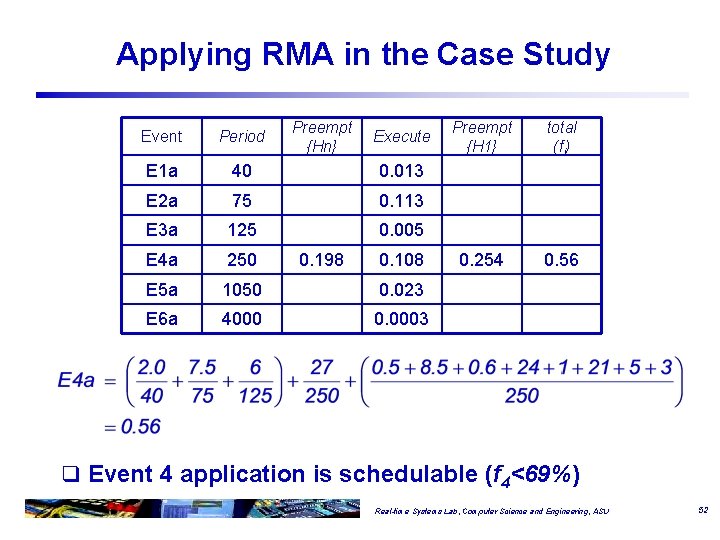
Applying RMA in the Case Study Preempt {Hn} Event Period E 1 a 40 0. 013 E 2 a 75 0. 113 E 3 a 125 0. 005 E 4 a 250 E 5 a 1050 0. 023 E 6 a 4000 0. 0003 0. 198 Execute 0. 108 Preempt {H 1} total (fi) 0. 254 0. 56 q Event 4 application is schedulable (f 4<69%) Real-time Systems Lab, Computer Science and Engineering, ASU 52

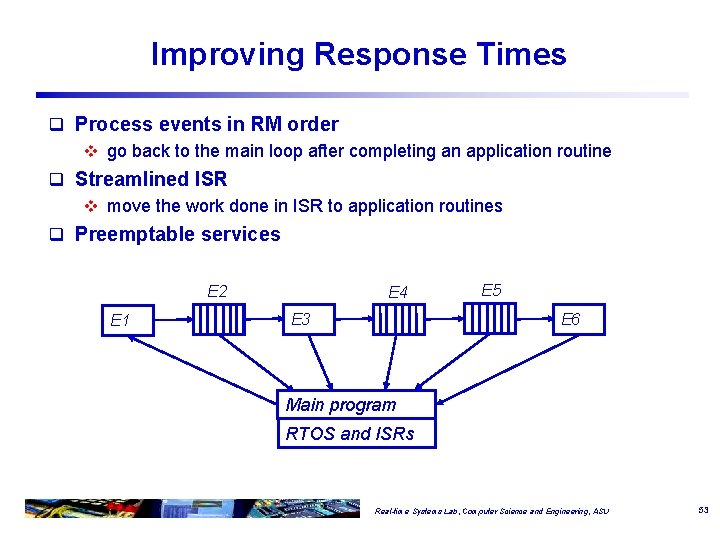
Improving Response Times q Process events in RM order v go back to the main loop after completing an application routine q Streamlined ISR v move the work done in ISR to application routines q Preemptable services E 2 E 1 E 4 E 3 E 5 E 6 Main program RTOS and ISRs Real-time Systems Lab, Computer Science and Engineering, ASU 53

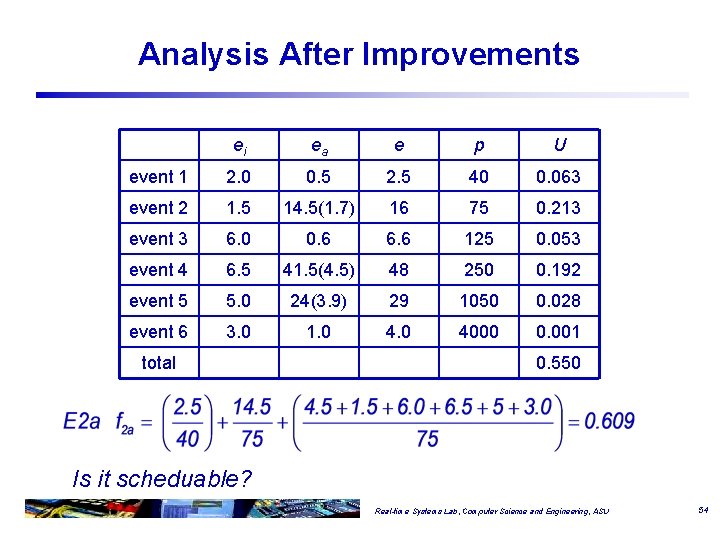
Analysis After Improvements ei ea e p U event 1 2. 0 0. 5 2. 5 40 0. 063 event 2 1. 5 14. 5(1. 7) 16 75 0. 213 event 3 6. 0 0. 6 6. 6 125 0. 053 event 4 6. 5 41. 5(4. 5) 48 250 0. 192 event 5 5. 0 24(3. 9) 29 1050 0. 028 event 6 3. 0 1. 0 4000 0. 001 total 0. 550 Is it scheduable? Real-time Systems Lab, Computer Science and Engineering, ASU 54