Schall Tne Klnge und Gerusche Was ist Schall

Schall – Töne, Klänge und Geräusche

Was ist Schall?

Versuche

Was kann man vom Schall sehen und fühlen? • Was kann man sehen und fühlen. . . • 1. Versuch: hüpfenden Kügelchen • 2. Versuch: 2 Tambolines mit Pendel http: //www. quarks. de/hoeren/0202. htm • 3. Versuch: Stimmgabel ins Wasser halten • Andere Versuche? • -> Schall hat etwas mit Bewegung zu tun

Wellenberg http: //www. kettering. edu/~drussell/Demos/waves-intro. html • Die einzelnen Seilstücke werden transversal ausgelenkt • An der Wand wird der Wellenberg invertiert = Phasensprung • Grund für Phasensprung: Die Wand reagiert auf die aufwärts gerichtete Kraft des ankommenden Wellenberges mit einer Gegenkraft in die entgegen gesetzte Richtung.

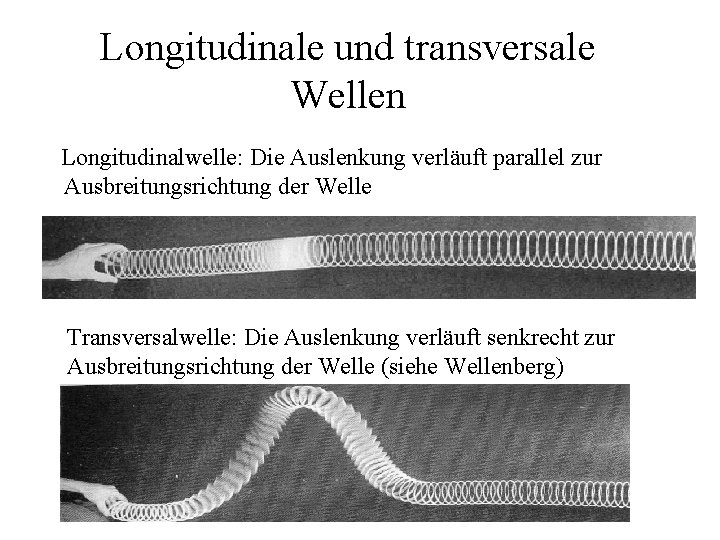
Longitudinale und transversale Wellen Longitudinalwelle: Die Auslenkung verläuft parallel zur Ausbreitungsrichtung der Welle Transversalwelle: Die Auslenkung verläuft senkrecht zur Ausbreitungsrichtung der Welle (siehe Wellenberg)

Wellen • Wie kann man Wellen erzeugen? • Eine Welle ist eine Störung, die sich in einem Medium ausbreitet. • Was für Störungen gibt es? • Wie sieht die Störung beim Tambolinversuch aus oder beim Versuch mit den hüfenden Kugeln oder beim Schall?

Schallwellen physikalisch gesehen • Physikalisch gesehen entsteht Schall durch eine wellenförmige Fortpflanzung einer Druck- und Dichteschwankungen in einem Medium. • Die Störungen pflanzen sich durch Wechselwirkung der Moleküle im Medium aus. • In Luft breiten sich longitudinale Wellen aus.

Physiker unterscheiden • Ton • Klang • Geräusch

Ton • Physikalisch gesprochen ist ein echter Ton ein Schallereignis, das nur aus einer Sinuswelle besteht.

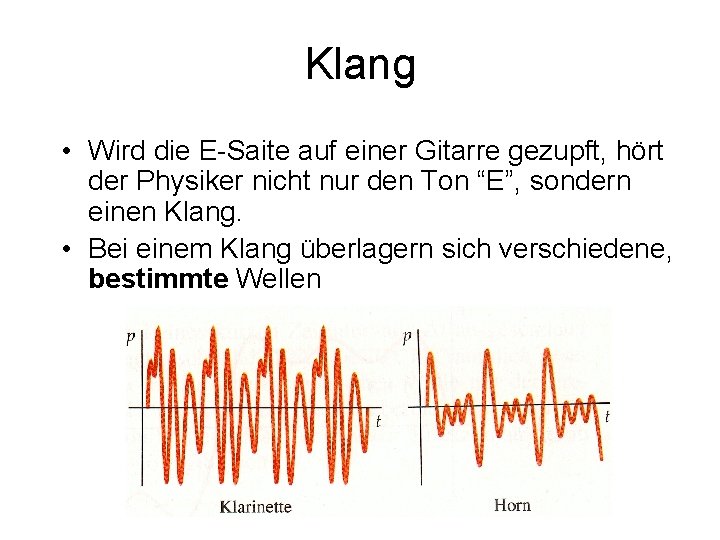
Klang • Wird die E-Saite auf einer Gitarre gezupft, hört der Physiker nicht nur den Ton “E”, sondern einen Klang. • Bei einem Klang überlagern sich verschiedene, bestimmte Wellen

Versuche: Ton und Klang mit Cassy

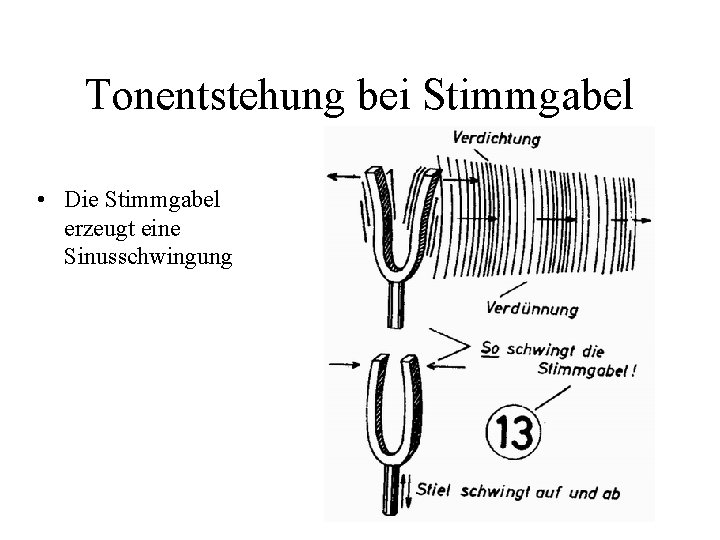
Tonentstehung bei Stimmgabel • Die Stimmgabel erzeugt eine Sinusschwingung

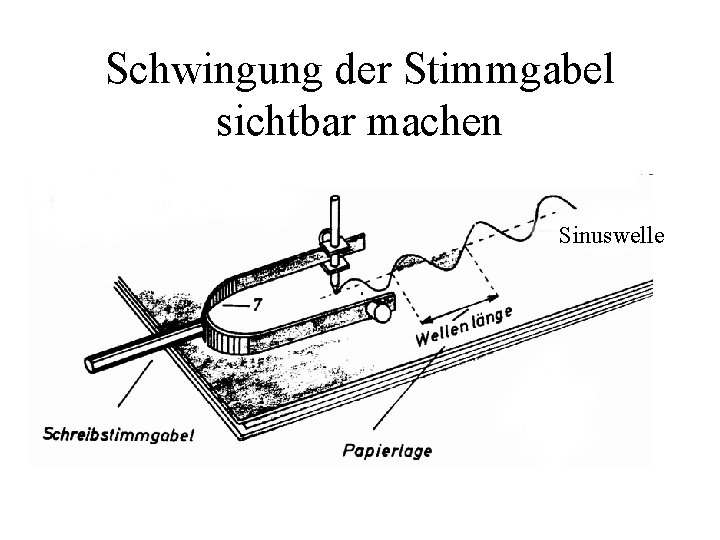
Schwingung der Stimmgabel sichtbar machen Sinuswelle

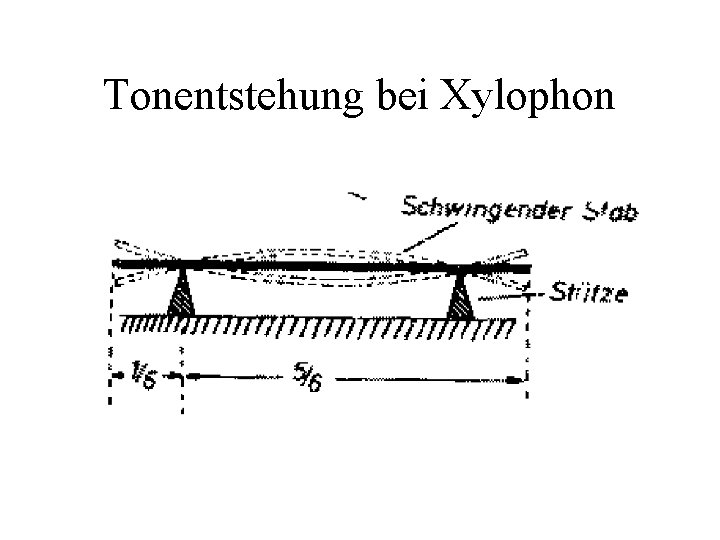
Tonentstehung bei Xylophon

Beim Klang überlagern sich: Grundton und Obertöne • Die Flöte (oder Klarientee, oder…) produziert nicht nur den Ton E, sondern neben der Grundschwingung so genannte "Obertöne“ oder “Harmonische”. • Obertöne haben ein Mehrfaches der Frequenz des jeweiligen Grundtons. • Die Gesamtheit von Grundton und Obertönen ergibt das Frequenzspektrum eines Klangs.

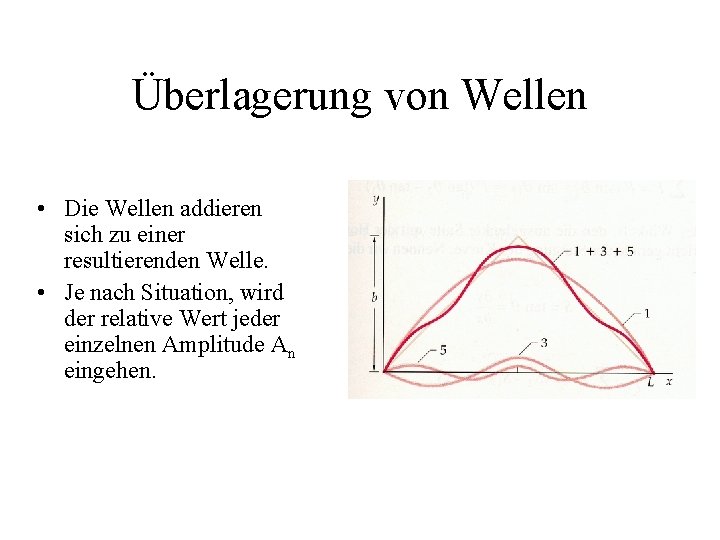
Überlagerung von Wellen • Die Wellen addieren sich zu einer resultierenden Welle. • Je nach Situation, wird der relative Wert jeder einzelnen Amplitude An eingehen.

Charakteristische Klang • Das Spektrum der Obertöne bestimmt den charakteristischen Klang eines Instruments. • Ein “Klang" klingt umso voller und wärmer, je mehr Obertöne ihn begleiten. • Bei einer Geige sind es mehr und stärkere Obertöne als bei einer Flöte.

Obertöne oder Harmonische bilden sich entsprechend den geometrischen Randbedingungen aus

Versuch : Stehende Seilwellen

Obertöne oder Harmonische beidseitig eingespannter Seite • Versuchsergebnis: • Es bilden sich stehende Wellen, die je nach Erregerfrequenz unterschiedliche Wellenlängen besitzen. • An den Enden befinden sich Schwingungsknoten • Je größer die Frequenz, umso kleiner die Wellenlänge, da v = f*λ. (v = Geschwindigkeit, f = Frequenz, λ = Wellenlänge)

Stehende Wellen beidseitig eingespannten Seil • Freihandversuch: fest gebundenes Seil

Entstehung einer stehenden Welle http: //www. kettering. edu/~drussell/Demos/superposition. html • Stehende Wellen entstehen durch Reflektion, • das heißt, es überlagern sich zwei Wellen, die sich addieren: • Y(x, t) = Asin (kx-ωt) + A sin (kx+ωt). • Additionstheorems: sinθ 1 + sinθ 2 = 2 * cos 0, 5 (θ 1 -θ 2) sin 0, 5 (θ 1+θ 2), (θ 1 = kx+ ωt und θ 2 = kx-ωt) • -> Y(x, t) = 2 A cos (ωt) sin (kx) • Dies ist eine stehende Welle, da Zeit- und Ortsterm voneinander unabhängig sind.

Stehende Wellen beidseitig eingespannten Seil und beidseitig geschlossenem Rohr • Für alle Wellenlängen λn gilt: L = n* (λn/2) • Entsprechend gilt für die Frequenzen: νn= n*(v/2 L) = n* ν 1 • • • L = Länge des Rohres, v = Schallgeschwindigkeit, n= 1, 2, 3, …, νn = Frequenz in Abhängigkeit von n, λn = Wellenlänge in Abhängigkeit von n

Versuch: Stehende Wellen bei einseitig offenem Rohr

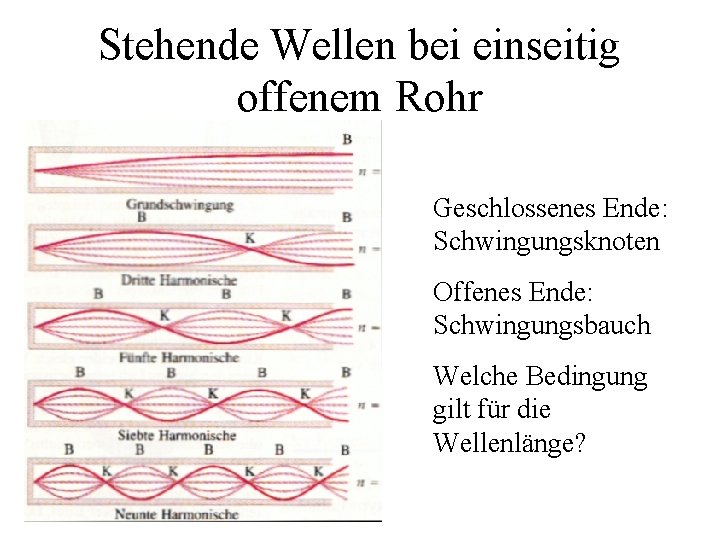
Stehende Wellen bei einseitig offenem Rohr Geschlossenes Ende: Schwingungsknoten Offenes Ende: Schwingungsbauch Welche Bedingung gilt für die Wellenlänge?

Bedingung für stehende Wellen bei einseitig offenem Rohr und einseitig eingespanntem Seil: L = n* (λn/4) υn = n*(v/4 L) n = 1, 3, 5, . . . (L = Länge des Rohres, λ = Wellenlänge, υ = Frequenz, v = Geschwindigkeit n = 1, 3, 5, . . . ) L

Versuch: Stehende Welle beidseitig offenem. Rohr

Bedingungen für stehende Wellen beidseitig offenem Rohr • Schwingungsbäuche an beiden Seiten des Rohres • L = n*(λ/2)

Chladni-Figuren Die Figuren entstehen, indem man mit einem Geigenbogen am Rand des Metalltellers streicht

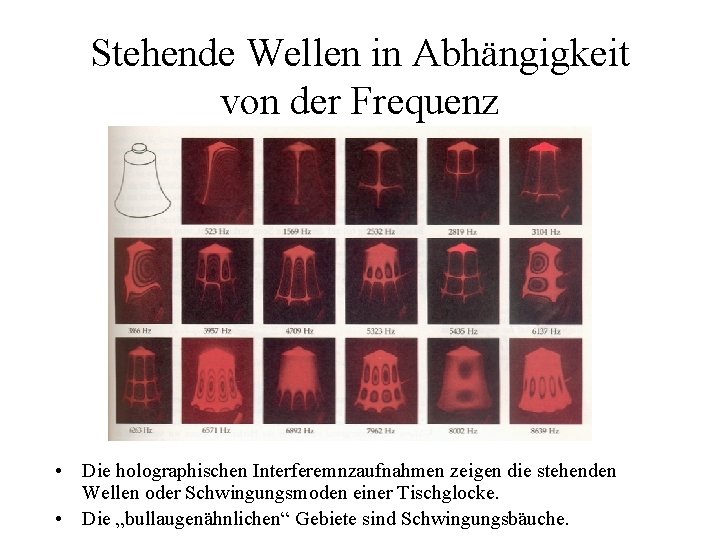
Stehende Wellen in Abhängigkeit von der Frequenz • Die holographischen Interferemnzaufnahmen zeigen die stehenden Wellen oder Schwingungsmoden einer Tischglocke. • Die „bullaugenähnlichen“ Gebiete sind Schwingungsbäuche.

Zusammenfassung • Die durch die Geometrie vorgegeben Grundtöne und Obertöne sind stehende Wellen. • Die stehenden Wellen überlagern sich und bilden so einen für die Geometrie des Körpers charakteristischen Klang