Scattering and diffraction Based on chapter 2 3

Scattering and diffraction (Based on chapter 2, 3, 4 in Williams and Carter)

Learning outcome • Know what is : – Elastic scattering, coherent scattering, incident beam, direct beam, cross section, differential cross section, mean free path, Airy disc, major semiangles, Fraunhofer and Fresnel diffraction • Possible scattering processes – Typical scattering angles, effect of Z and U etc

Scattering-Diffraction • When do we talk about A) Scattering? B) Diffraction? Incident beam Scattered/diffracted beam Direct beam

Scattering and diffraction • Particles are scattered/deflected • Waves are diffracted A single scattering event is dependent on U and Z Scattering from a specimen is influenced by its thickness, density, crystallinity, angle of the incident beam.

• Why are electrons scattered in the specimen? • How can the scattering process affect the energy and the coherency of the incident electrons?

Electron scattering • What is the probability that an electron will be scattered when it passes near an atom? – The idea of a cross section, σ • If the electron is scattered, what is the angle through which it is deviated? – Used to control which electrons form the image • What is the average distance an electron travels between scattering events? – The mean free path, λ • Does the scattering event cause the electrons to lose energy or not? – Distinguishing elestic and inelastic scattering

Some definitions • Single scattering: 1 scattering event • Plural scattering: 1 -20 scattering events • Multiple scattering: >20 scattering events • Forward scattered: scattered through < 90 o • Bacscattered: scattered through > 90 o As the specimen gets thicker more electrons are back scattered

X-rays versus electrons • X-rays are scattered by the electrons in a material • Electrons are scattered by both the electron and the nuclei in a material – The electrons are directly scattered and not by an field to field exchange as in the case for X-rays • The scattering process is not important for diffraction

Electron scattering • Elastic – The kinetic energy is unchanged – Change in direction relative to incident electron beam • Inelastic – The kinetic energy is changed (loss of energy) – Energy form the incident electron is transferred to the electrons and atoms in the specimen • Coherent – Elastically scattering electrons are usually coherent • Incoherent – Inelastic electrons are usually incoherent (low angles (<1 o)) – Elastic scattering to higher angles (>~10 o)

Interaction cross section The chance of a particular electron undergoing any kind of interaction with an atom is determined by an interaction cross section (an area). σatom=πr 2 r has different value for each scattering process and depends on E 0 When divided by the actual area of the atom the it represents the probability that a scattering event will occure. Elastic scattering from an isolated atom: Radius of the scatteing field of the nucleus and the electron : re=e/Vθ rn=Ze/Vθ

Differential cross section d σ/dΩ The differential cross section dσ/dΩ describes the angular distribution of scattering from an atom, and is a measure of the probability for scattering in a solid angle dΩ.

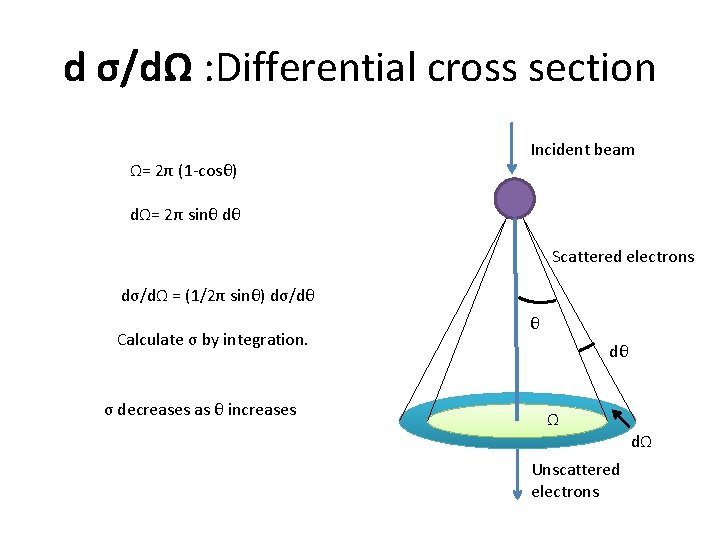
d σ/dΩ : Differential cross section Ω= 2π (1 -cosθ) Incident beam dΩ= 2π sinθ dθ Scattered electrons dσ/dΩ = (1/2π sinθ) dσ/dθ Calculate σ by integration. σ decreases as θ increases θ dθ Ω dΩ Unscattered electrons

Scattering form the specimen Total scattering cross section/The number of scattering events per unit distance that the electrons travels through the specimen: σtotal=Nσatom= Noσatom ρ/A N= atoms/unit volume No: Avogadros number, ρ: density of pecimen, A: atomic weight of the scattering atoms If the specimen has a thickness t the probability of scattering through the specimen is: tσtotal=Noσatom ρt/A

Some numbers • For 100 -400 ke. V – The elastic cross section is almost always the dominant component of the total scattering. – 100 ke. V: • σelastic = ~10 -22 m 2 • σinelastic = ~10 -22 - 10 -26 m 2 See examples of σ in Figure 4. 1 – Typical scattering radius: r ~ 0. 01 nm

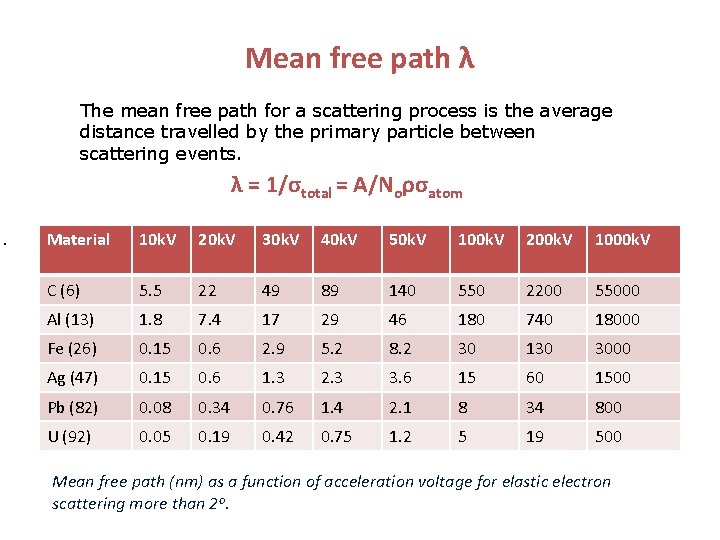
Mean free path λ The mean free path for a scattering process is the average distance travelled by the primary particle between scattering events. λ = 1/σtotal = A/Noρσatom Material 10 k. V 20 k. V 30 k. V 40 k. V 50 k. V 100 k. V 200 k. V 1000 k. V C (6) 5. 5 22 49 89 140 550 2200 55000 Al (13) 1. 8 7. 4 17 29 46 180 740 18000 Fe (26) 0. 15 0. 6 2. 9 5. 2 8. 2 30 130 3000 Ag (47) 0. 15 0. 6 1. 3 2. 3 3. 6 15 60 1500 Pb (82) 0. 08 0. 34 0. 76 1. 4 2. 1 8 34 800 U (92) 0. 05 0. 19 0. 42 0. 75 1. 2 5 19 500 Mean free path (nm) as a function of acceleration voltage for elastic electron scattering more than 2 o.

Electron scattering The probability of scattering is described in terms of either an “interaction cross-section” or a mean free path. Mote Carlo simulations: http: //www. matter. org. uk/TEM/electron_scattering. htm# • Elastic – The kinetic energy is unchanged – Change in direction relative to incident electron beam • Inelastic – The kinetic energy is changed (loss of energy) – Energy form the incident electron is transferred to the electrons and atoms in the specimen

Elastic scattering • Major source of contrast in TEM images • Scattering from an isolated atom – From the electron cloud: few degrees of angular deviation – From the positive nucleus: up to 180 o

Scattering • Eleastic scattering is the major source of contrast in TEM images • Scattering from an isolated atom – From the electron cloud: few degrees of angular deviation – From the positive nucleus: up to 180 o Fig. 3. 1 Williams and Carter

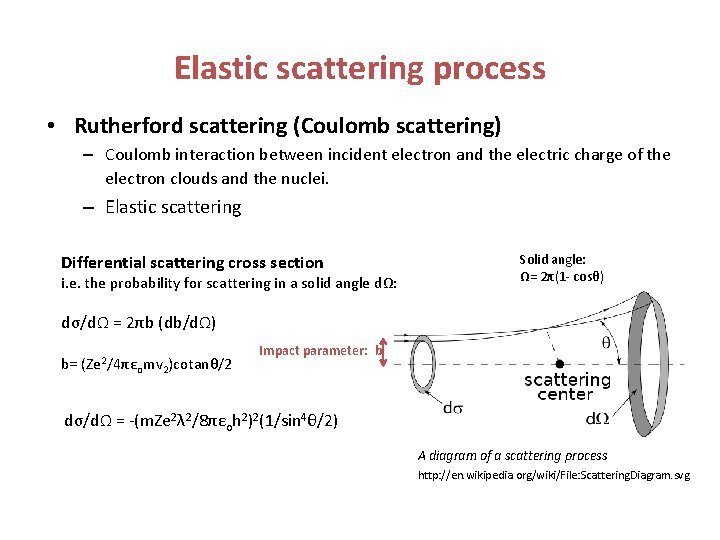
Elastic scattering process • Rutherford scattering (Coulomb scattering) – Coulomb interaction between incident electron and the electric charge of the electron clouds and the nuclei. – Elastic scattering Differential scattering cross section i. e. the probability for scattering in a solid angle dΩ: Solid angle: Ω= 2π(1 - cosθ) dσ/dΩ = 2πb (db/dΩ) b= (Ze 2/4πε omv 2)cotanθ/2 Impact parameter: b dσ/dΩ = -(m. Ze 2λ 2/8πεoh 2)2(1/sin 4θ/2) A diagram of a scattering process http: //en. wikipedia. org/wiki/File: Scattering. Diagram. svg

Atomic scattering factor f(θ) • | f(θ)|2=dσ/dΩ • f(θ) is a measure of amplitude of an electron wave scattered from an isolated atom • | f(θ)|2 is proportional to the scattered intesity

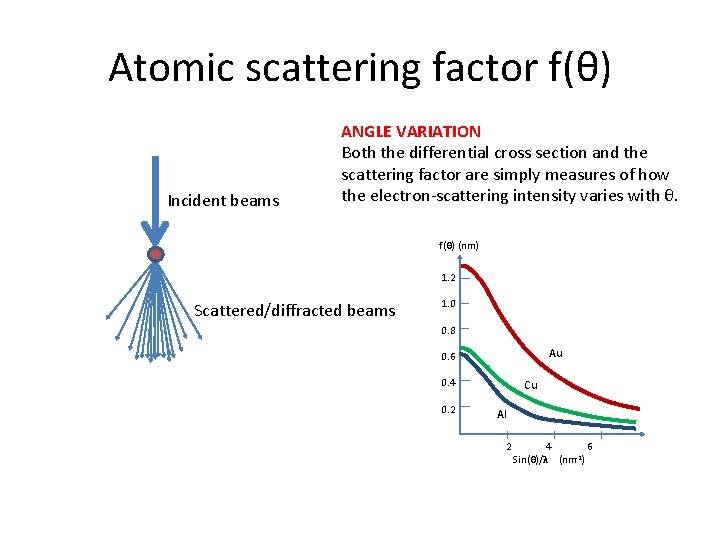
Atomic scattering factor f(θ) Incident beams ANGLE VARIATION Both the differential cross section and the scattering factor are simply measures of how the electron-scattering intensity varies with θ. f(θ) (nm) 1. 2 Scattered/diffracted beams 1. 0 0. 8 Au 0. 6 0. 4 0. 2 Cu Al 2 4 6 Sin(θ)/λ (nm-1)

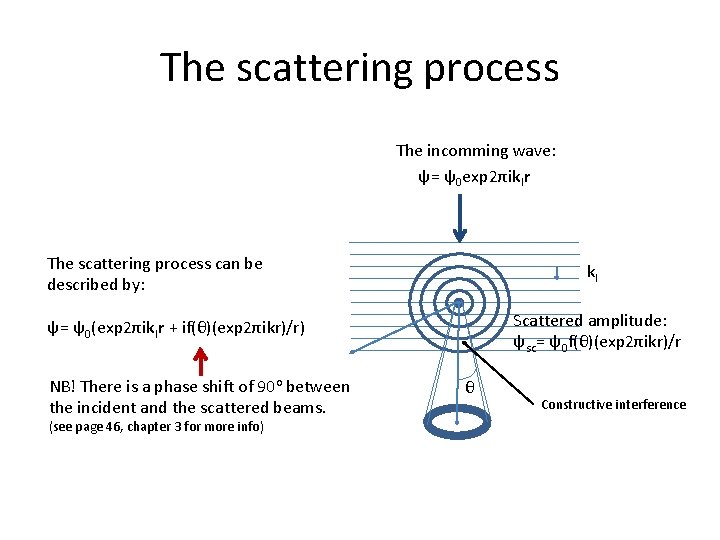
The scattering process The incomming wave: ψ= ψ0 exp 2πik. Ir The scattering process can be described by: k. I Scattered amplitude: ψsc= ψ0 f(θ)(exp 2πikr)/r ψ= ψ0(exp 2πik. Ir + if(θ)(exp 2πikr)/r) NB! There is a phase shift of 90 o between the incident and the scattered beams. (see page 46, chapter 3 for more info) θ Constructive interference

The structure factor F(θ) Acel=(exp 2πikr)/r Σfi(θ)exp 2πi. K. ri K=? and ri= ? F(θ) is a measure of the amplitude scattered by a unit cell of a crystal structure The intensity: IF(θ)I 2 Under specific conditions, electrons scattering in a crystal may result in ZERO scattered intensity.

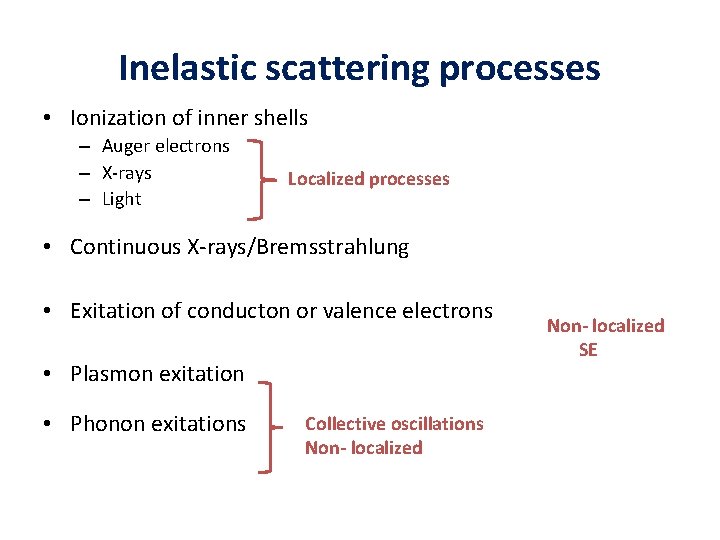
Inelastic scattering processes • Ionization of inner shells – Auger electrons – X-rays – Light Localized processes • Continuous X-rays/Bremsstrahlung • Exitation of conducton or valence electrons • Plasmon exitation • Phonon exitations Collective oscillations Non- localized SE

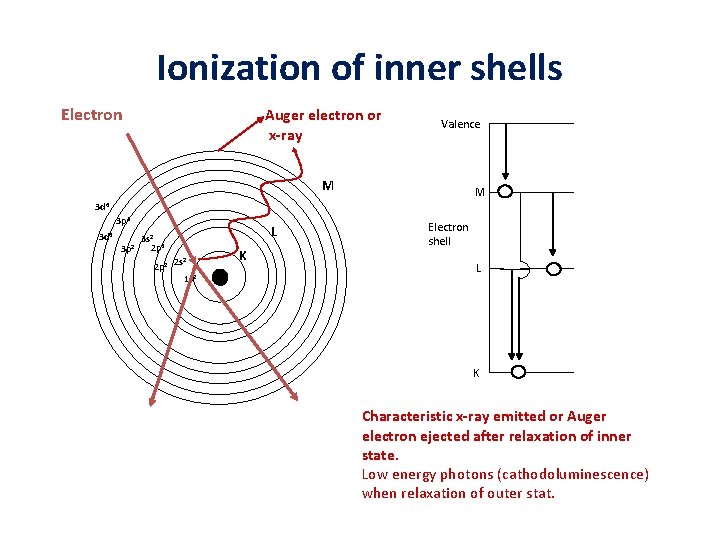
Ionization of inner shells Electron Auger electron or x-ray Valence M M 3 d 6 3 p 4 3 d 4 L 3 s 2 2 2 p 4 3 p 2 p 2 2 s 2 1 s 2 K Electron shell L K Characteristic x-ray emitted or Auger electron ejected after relaxation of inner state. Low energy photons (cathodoluminescence) when relaxation of outer stat.

Auger electrons or x-rays EELS?

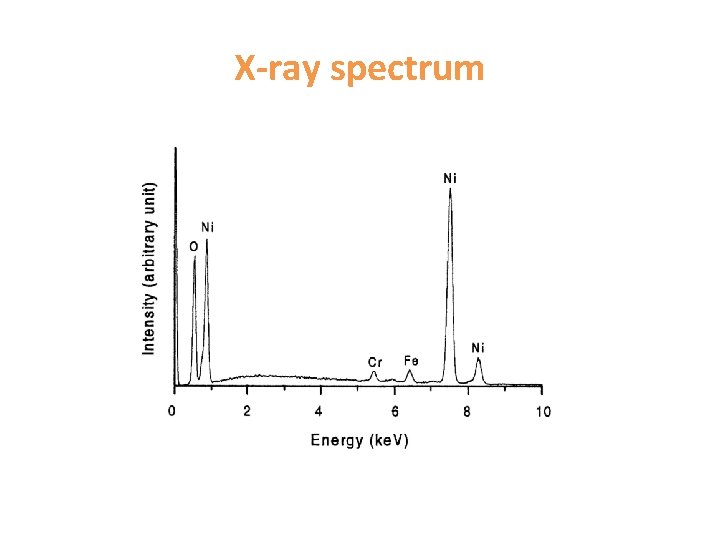
X-ray spectrum

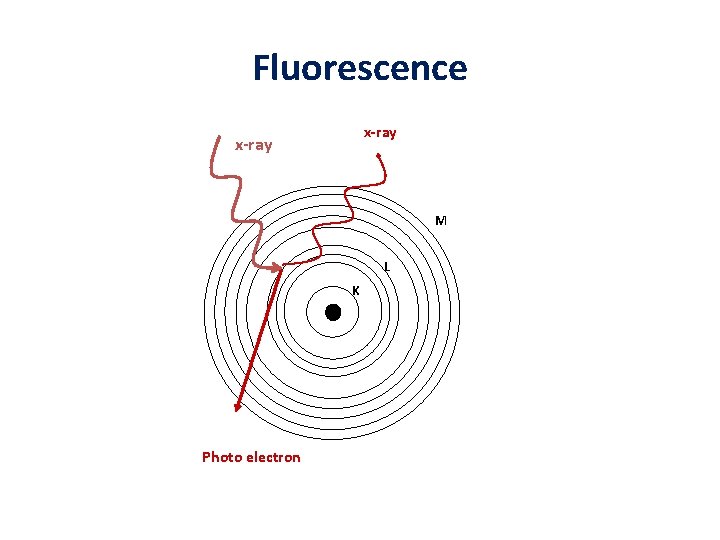
Fluorescence x-ray M L K Photo electron

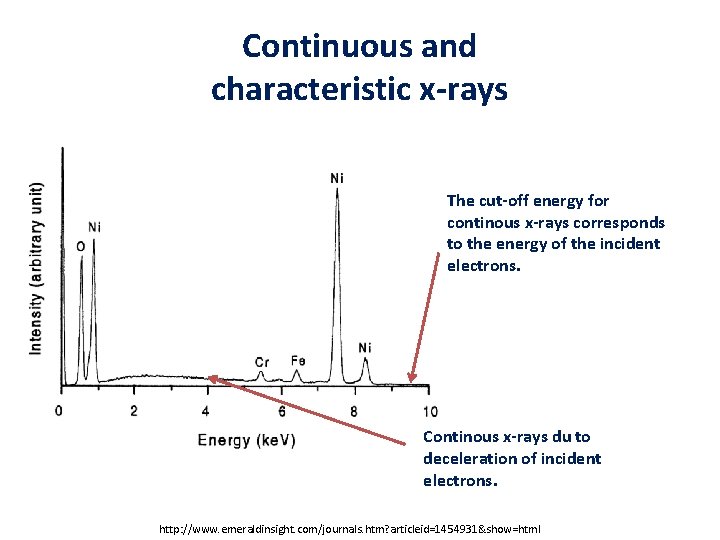
Continuous and characteristic x-rays The cut-off energy for continous x-rays corresponds to the energy of the incident electrons. Continous x-rays du to deceleration of incident electrons. http: //www. emeraldinsight. com/journals. htm? articleid=1454931&show=html

Secondary electrons (SEs) are electrons within the specimen that are ejected by the beam electrons. Electrons from the conduction or valence band. E ~ 0 – 50 e. V The secondary emission coefficient: Auger electrons δ=number of secondary electrons/numbers of primary electrons Dependent on acceleration voltage.

Cathodoluminescence Conduction band Valence band

Plasmon excitations The incoming electrons can interact with electrons in the ”electron gas” and cause the electron gas to oscillate. The oscillations are called plasmons. Plasmon frequency: ω=((ne 2/εom))1/2 Energy: Ep=(h/2π)ω Ep~ 10 -30 e. V, λp, 100 k. V ~150 nm n: free electron density, e: electron charge, εo: dielectric constant, m: electron mass

Phonon excitation Equivalent to specimen heating Energy losses ~ 0. 1 e. V The effect in the diffraction patterns: -Reduction of intensities (Debye-Waller factor) -Diffuce bacground between the Bragg reflections

EELS Sum of several losses Thin specimens

Fraunhofer and Fresnel diffraction • Far-field diffraction • Near-field diffraction

Diffraction from slits and holes • Young`s slitt experiment • Phasor diagram • Airy disk

Angles and diffraction patterns • Figure 2. 12 – Beam convergence angle, α – Collection angle, β – Scattering semiangle, θ Diffraction patterns: Picture of the distribution of scattered electrons Fig. 2. 13 Williams and Carter