Scattering Amplitudes Song He Institute of Theoretical Physics






































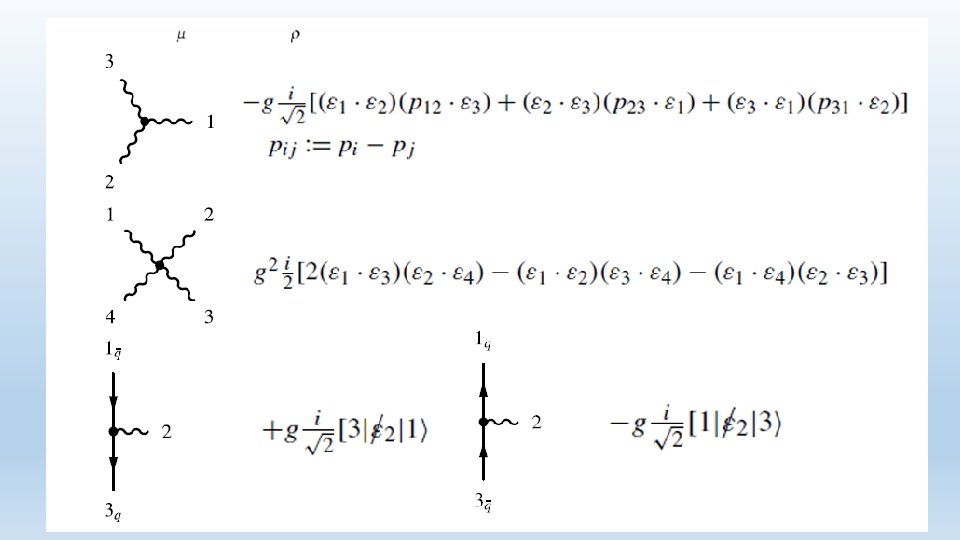







- Slides: 55

Scattering Amplitudes Song He Institute of Theoretical Physics, Chinese Academy of Sciences , Beijing

Motivations: QFT and Amplitudes

Quantum Field Theory (QFT) • Our theoretical framework to describe Nature • Essentially the consequence of two major principles

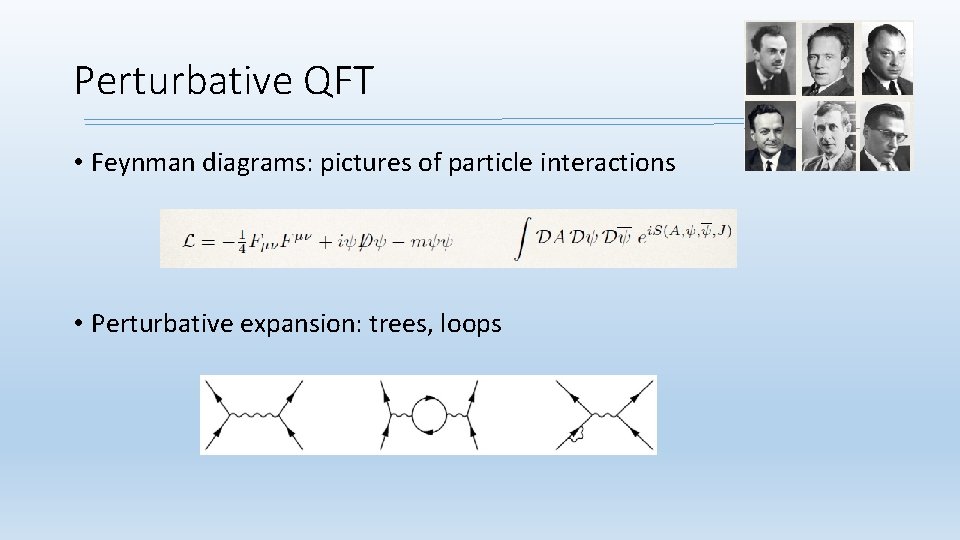
Perturbative QFT • Feynman diagrams: pictures of particle interactions • Perturbative expansion: trees, loops

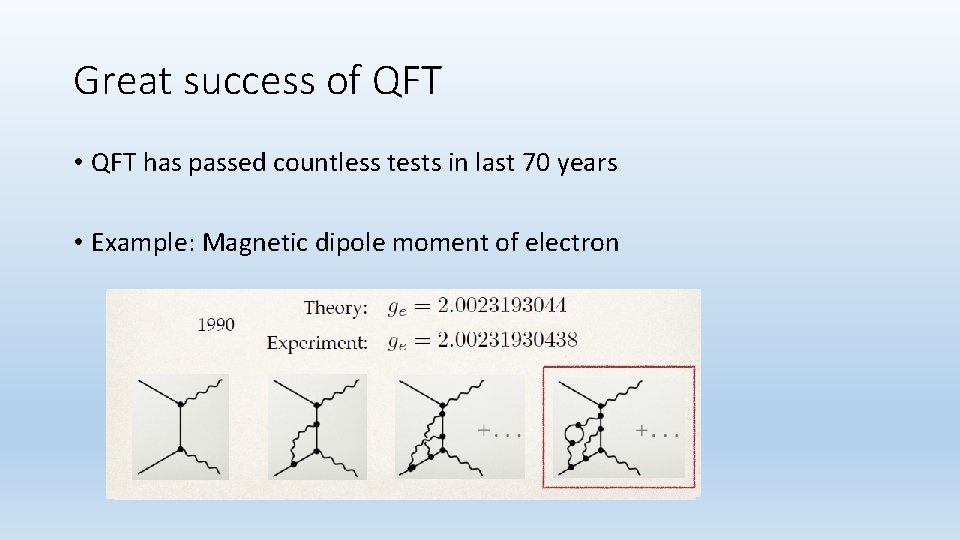
Great success of QFT • QFT has passed countless tests in last 70 years • Example: Magnetic dipole moment of electron

Incomplete picture • Our understanding of QFT is incomplete! • Also, tension with gravity and cosmology If there is a new way of thinking about QFT, it must be seen even at weak coupling • Explicit evidence: scattering amplitudes

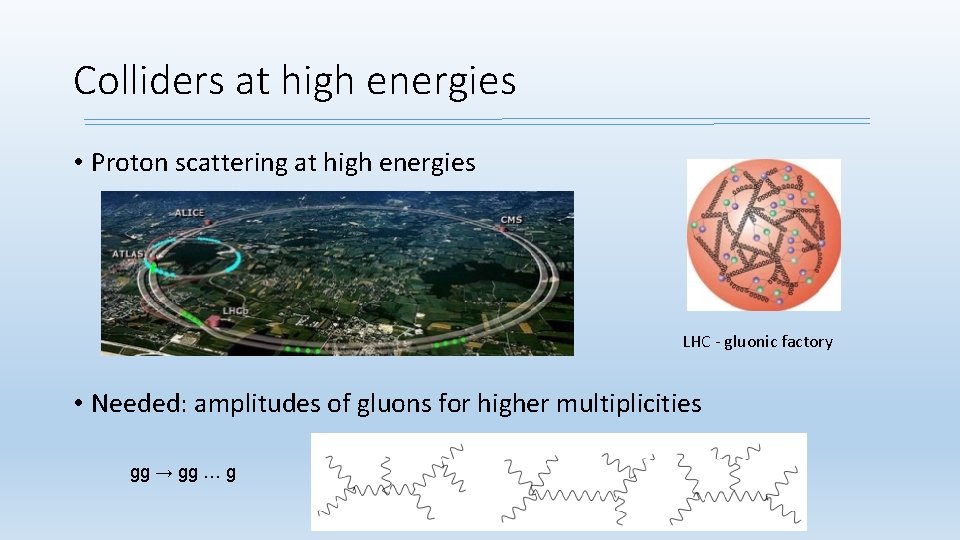
Colliders at high energies • Proton scattering at high energies LHC - gluonic factory • Needed: amplitudes of gluons for higher multiplicities gg → gg … g

Early 80 s • Status of the art: gg → ggg Brute force calculation 24 pages of result

New collider • 1983: Superconducting Super Collider approved • Energy 40 Te. V: many gluons! • Demand for calculations, next on the list: gg→gggg

Parke-Taylor formula(Parke, Taylor 1985) • Process : gg→gggg • 220 Feynman diagrams, ~ 100 pages of calculations • 1985: Paper with 14 pages of result

Parke-Taylor formula Within a year they realized

Parke-Taylor formula Within a year they realized

Birth of amplitudes

Spinor-Helicity Formalism

Spinors Lorentz group representations Infinitesimally with These are 6 generators of the Lorentz group: We see that the SO(1, 3) may be mapped to two commuting copies of SU(2)

Spinors Basis Weyl spinors Chiral solutions of the massless Dirac equation e. g.

Spinors Lower spin representations of 4 -D Lorentz group

Spinor-helicity formalism for massless particles For a massless particle

Spinor-helicity formalism for massless particles Requiring the four-momentum to be real with Lorentz-signature translates into the relation The sign in this relation follows the sign of the energy of the associated four-momentum An explicit realization

Spinor invariants of the two SU(2)’s By definition, Lorentz invariant objects= functions of spinor invariants (“angle” and “square” brackets) Mandelstam invariants For real momenta, we have

Spinor invariants anti-symmetry Momentum conversation Schouten Identity

Little group Rescaling freedom (little group) for real momenta for complex momenta

Little group Under little group scaling, the amplitude transforms homogeneously. e. g.

Helicity Lorentz invariant quantity for massless particles U(1) generator of helicity

Three point amplitudes Momentum conversation requires which is a singular kinematic point for real momenta! has two chirally conjugate solutions

Three point amplitudes The 3 -pt amplitude is non-singular, and completely fixed by Poincare invariance! Up to an overall constant solution 1: Little group scaling fixes for solution 2

Three point amplitudes Consider the special case of 3 pt amps with identical spin (s) particles e. g. --+ or but the second case is obviously non-local! Poincare + locality → MHV three point amplitudes

Gluon polarizations Basic properties (null, transverse, etc. ) are automatically satisfied

Gluon polarizations transforms like helicity +1

Gluon polarizations: 3 pt pick

Graviton polarization ~ 200 terms

Graviton polarization: 3 pt The on-shell amplitude is remarkable simple (the square of gluon 3 pt amplitudes!)

Graviton polarization: 4 pt thousands of terms Unimaginable to calculate 4 or more gravitons amplitudes by brute force

Gauge-theory Amps: Helicity, Color etc.

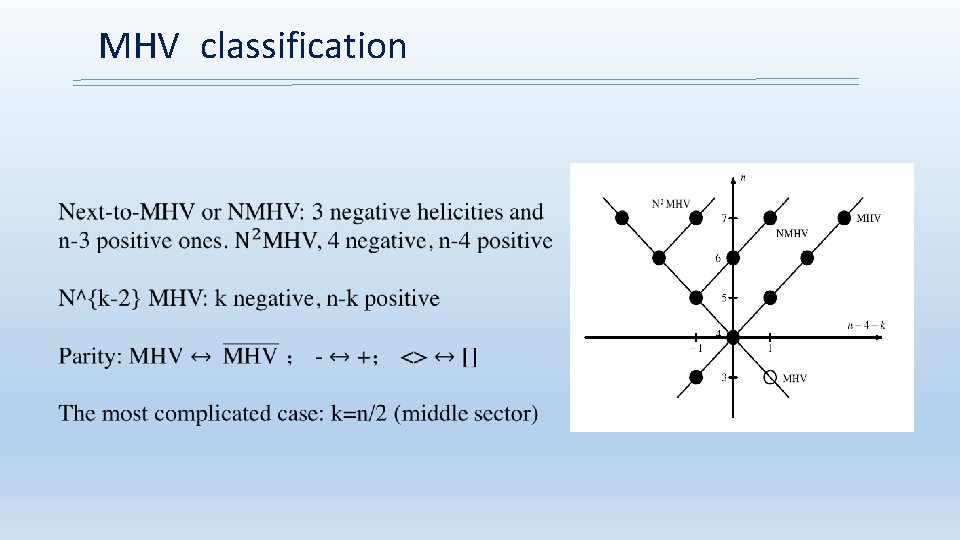
Helicity amplitudes Helicities of gluons (gravitons) +1 or -1 (+2 or -2) helicity amplitudes e. g. A(+++---), A(++----), A(--++++), … Huge simplifications, with different properties and structures! Number of negative-helicity gluons (gravitons): k k=0: k=1: k=n-1: k=n: A(+, +, +, …, +)=0 A(-, -, -, … , -)=0 A(-, +, +, …, +)=0 A(+, -, -, … , -)=0 both at tree level in general and For all loops with supersymmetries

Vanishing tree amplitudes

Vanishing tree amplitudes Similarly, the gluon tree-amplitude with one flipped helicity state vanishes which follows from the choice

Simplest amplitudes: MHV

MHV classification

Non-Abelian Gauge Theories invariant under the local gauge transformation

Feynman rules for non-abelian gauge theory

Color decompositions organize color d. o. f. → colors x kinematics → pieces with simpler analytic properties

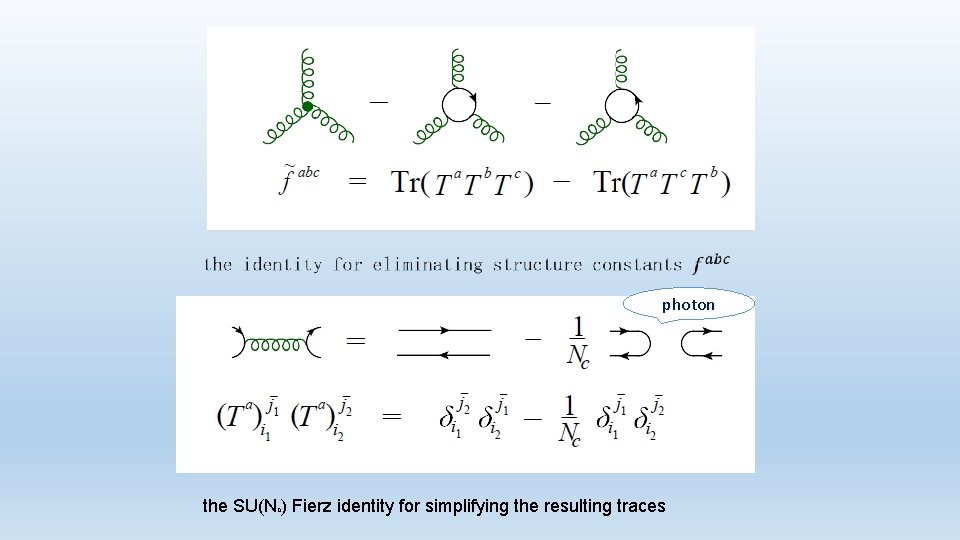
photon the SU(Nc) Fierz identity for simplifying the resulting traces

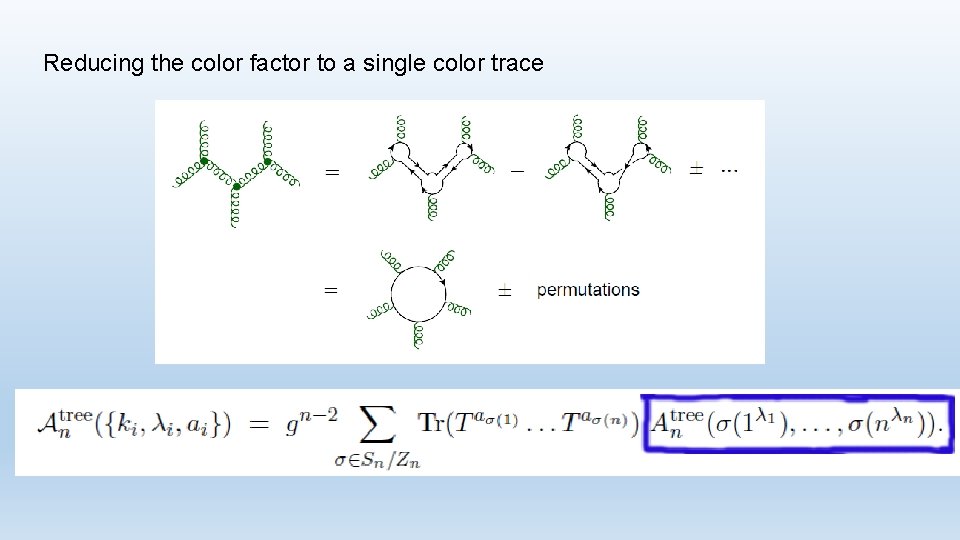
Reducing the color factor to a single color trace

Color-ordered amplitudes Gauge invariant This is a key object of our interest Different orderings related by permutations Color-summed cross section is indeed made up of color-ordered amplitudes simpler pole structure
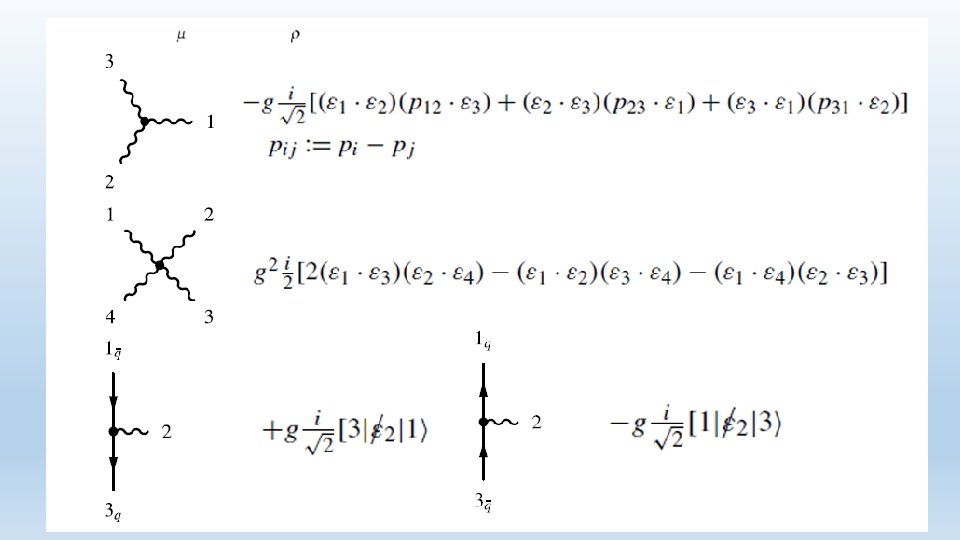
Color ordered Feynman rules

QCD amplitudes: e. g. similar decomposition for those with one fermion line

Properties of color-ordered amplitudes l Cyclicity l Reflection l U(1) decoupling

l Kleiss-Kuijf relations (fancy version of U(1) decoupling) l Bern-Carrasco-Johansson relations

Some Examples

A simple four-point example little group check

Other helicity structures exchanges labels 1 and 2 two other terms can be obtained by parity

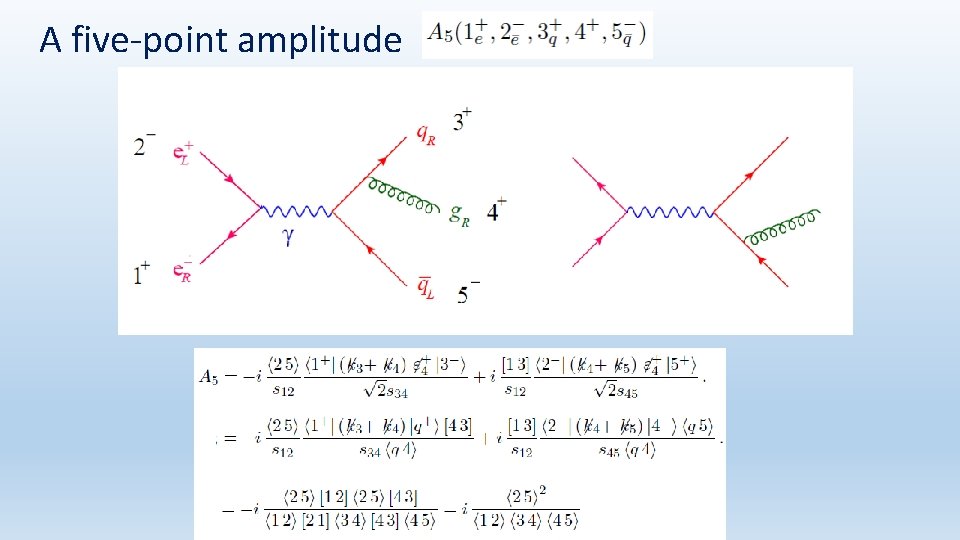
A five-point amplitude

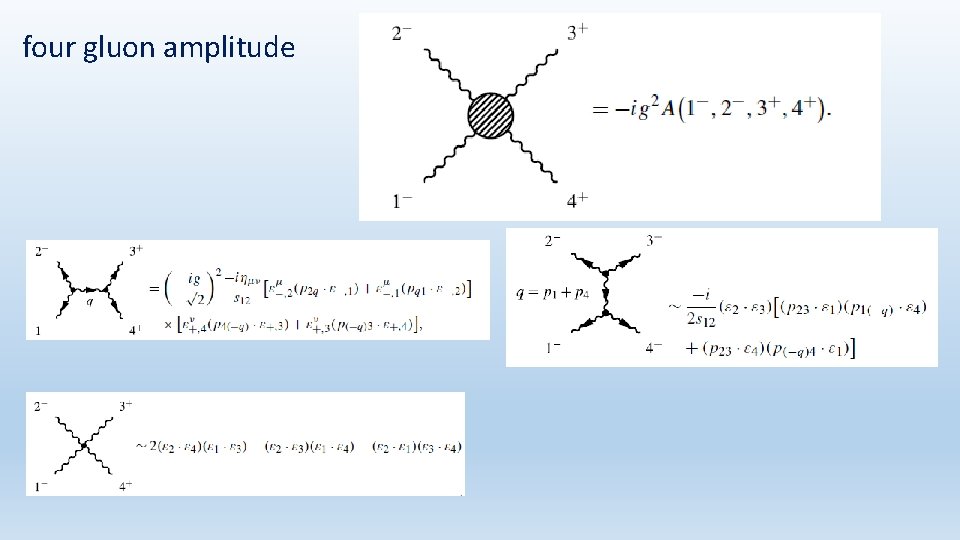
four gluon amplitude

A nice choice of reference left only 2 diagrams vanish