Scatter Diagrams Objectives D Grade Draw a scatter

Scatter Diagrams Objectives: D Grade Draw a scatter diagram by plotting points on a graph Interpret the scatter graph Draw a line of best fit C Grade Interpret the line of best fit Identify the type and strength of correlation

Scatter Diagrams A scatter graph is a graph using paired data that can be used to find out whethere is a relationship between two variables. paired data is two separate pieces of data referring to the same thing e. g. the age and value of a car the height and shoe size of a person the marks that a person gained in two separate tests. A variable is a piece of information that can change. e. g. test results - these can be any value, but will be a specific value for a particular person's test.

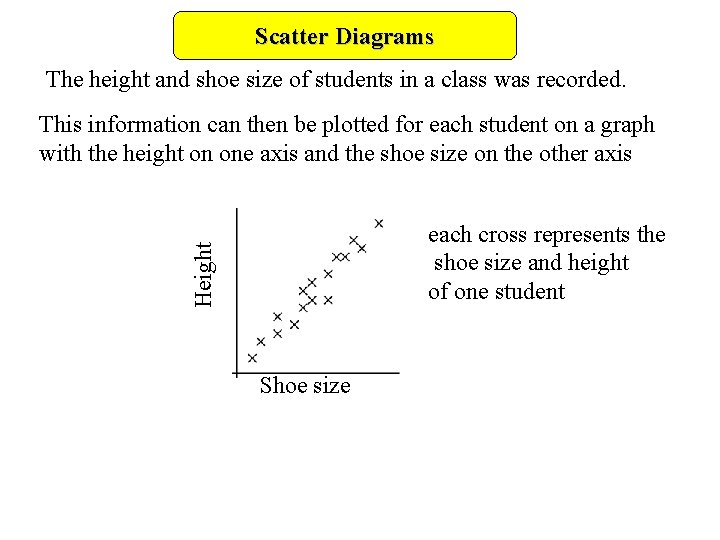
Scatter Diagrams The height and shoe size of students in a class was recorded. This information can then be plotted for each student on a graph with the height on one axis and the shoe size on the other axis Height each cross represents the shoe size and height of one student Shoe size

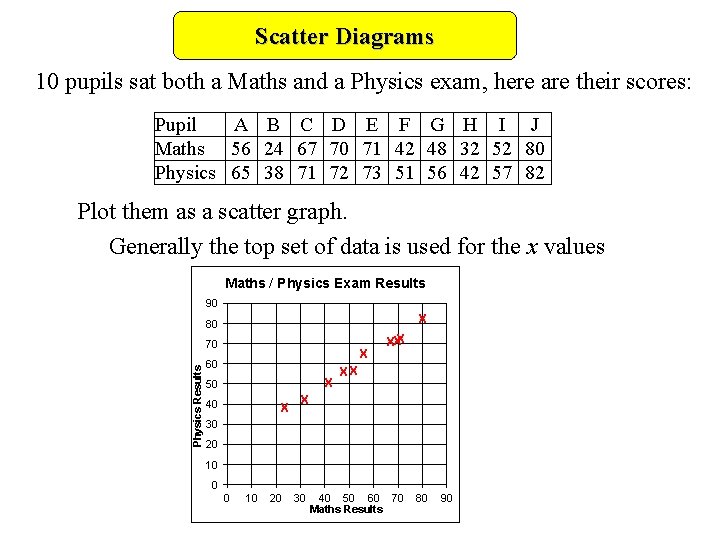
Scatter Diagrams 10 pupils sat both a Maths and a Physics exam, here are their scores: Pupil A B C D E F G H I J Maths 56 24 67 70 71 42 48 32 52 80 Physics 65 38 71 72 73 51 56 42 57 82 Plot them as a scatter graph. Generally the top set of data is used for the x values Maths / Physics Exam Results 90 X 80 Physics Results 70 X 60 X 50 40 X XX X 30 20 10 0 0 10 20 30 40 50 60 70 Maths Results 80 90

Scatter Diagrams Correlation: is a measure of the relationship between two variables; correlation is measure in terms of type and strength correlation is assessed by being strong or weak strong means there is a very strong relationship such as ‘the hotter the weather the more ice creams are sold’ weak means there is no relationship between things such as ‘the colder the weather the better my exam results will be’

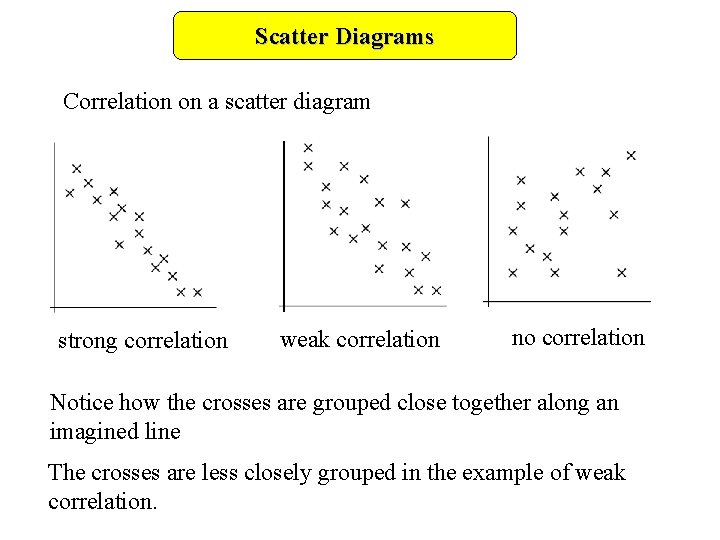
Scatter Diagrams Correlation on a scatter diagram strong correlation weak correlation no correlation Notice how the crosses are grouped close together along an imagined line The crosses are less closely grouped in the example of weak correlation.

Scatter Diagrams Correlation can also be described and positive or negative, Depending on the slope (gradient) of the graph positive correlation negative correlation Positive correlation means that as one item increases, so does the other. e. g. as a person’s height increases so does their armspan Negative correlation means that as one item increases, so does the other. e. g. as a car gets older its value decreases

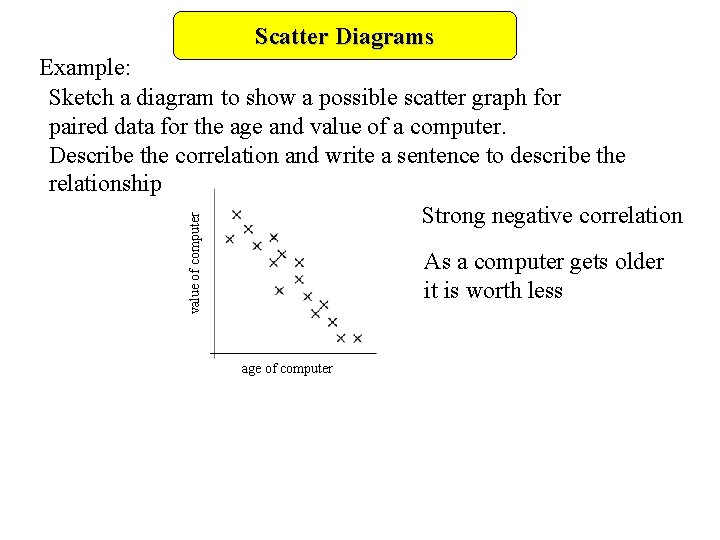
Scatter Diagrams value of computer Example: Sketch a diagram to show a possible scatter graph for paired data for the age and value of a computer. Describe the correlation and write a sentence to describe the relationship Strong negative correlation As a computer gets older it is worth less age of computer

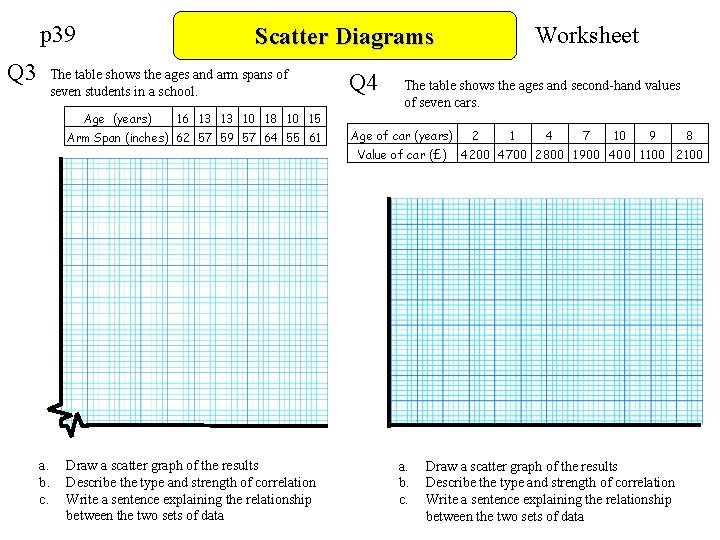
p 39 Q 3 The table shows the ages and arm spans of seven students in a school. Age (years) 16 13 13 10 18 10 15 Arm Span (inches) 62 57 59 57 64 55 61 Q 4 The table shows the ages and second-hand values of seven cars. Age of car (years) Value of car (£) a. b. c. Worksheet Scatter Diagrams Draw a scatter graph of the results Describe the type and strength of correlation Write a sentence explaining the relationship between the two sets of data a. b. c. 2 1 4 7 10 9 8 4200 4700 2800 1900 400 1100 2100 Draw a scatter graph of the results Describe the type and strength of correlation Write a sentence explaining the relationship between the two sets of data

Scatter Diagrams Q 5 The table shows the daily rainfall and the number Of sunbeds sold at a resort on the south coast Amount of rainfall (mm) 0 1 2 5 6 9 Q 8 refer to book p 40 11 Number of sunbeds sold 380 320 340 210 220 110 60 a. b. c. Draw a scatter graph of the results Describe the type and strength of correlation Write a sentence explaining the relationship between the two sets of data Worksheet

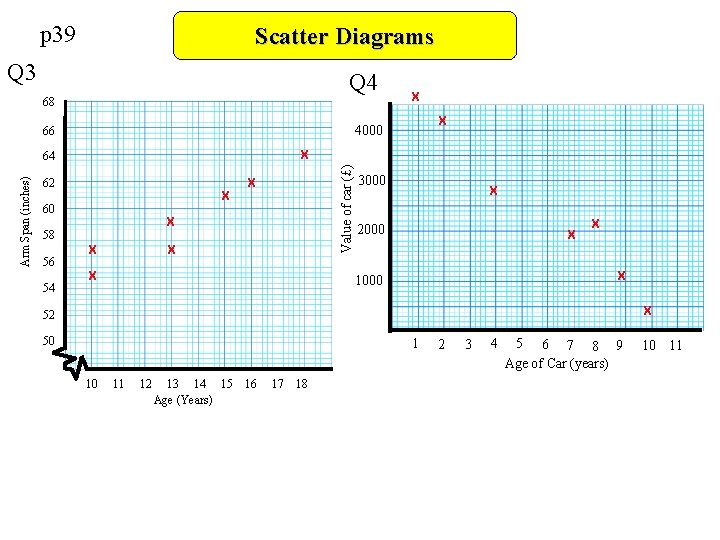
p 39 Scatter Diagrams Q 3 Q 4 68 X 62 X 60 Value of car (£) Arm Span (inches) 64 X X 58 54 X 4000 66 56 X X 3000 X 2000 X X X 1000 X 52 50 1 10 11 12 13 14 15 Age (Years) 16 17 18 2 3 4 5 6 7 8 9 Age of Car (years) 10 11

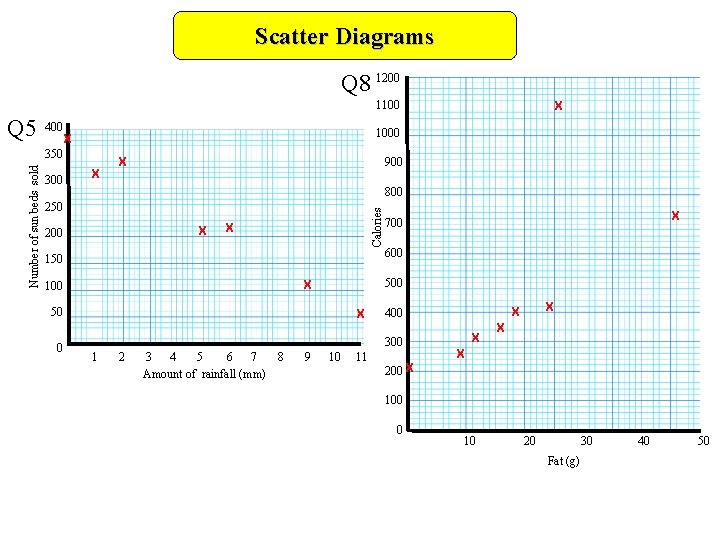
Scatter Diagrams Q 8 1200 1100 400 1000 X Number of sun beds sold 350 300 X X 900 800 250 X 200 Calories Q 5 X 150 50 X 600 2 3 4 5 6 7 Amount of rainfall (mm) 8 9 10 11 X X 400 300 1 X 700 500 X 100 0 X X 200 X 100 0 10 20 30 Fat (g) 40 50