Scanning Inflation and Reheating Topdown approach to inflation

Scanning Inflation and Reheating Top-down approach to inflation: seeks to embed it in fundamental theory Bottom-up approach to inflation: reconstruction of acceleration trajectories Lev Kofman, CITA Cosmo 05, Bonn September 1, 2005

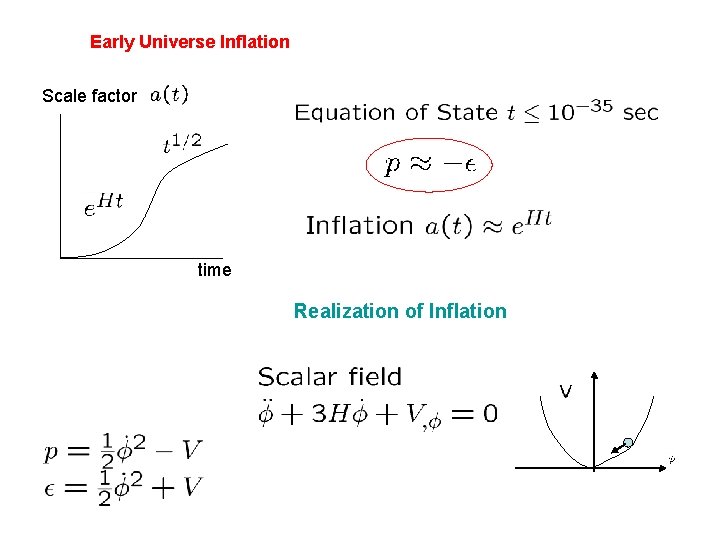
Early Universe Inflation Scale factor time Realization of Inflation

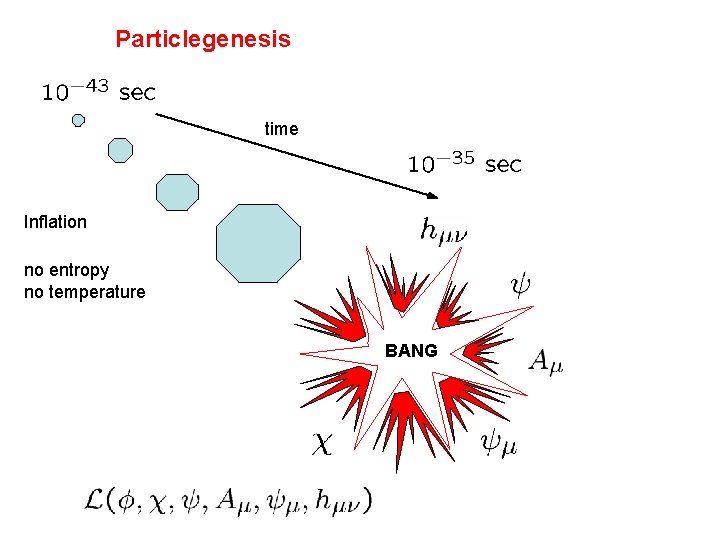
Particlegenesis time Inflation no entropy no temperature BANG

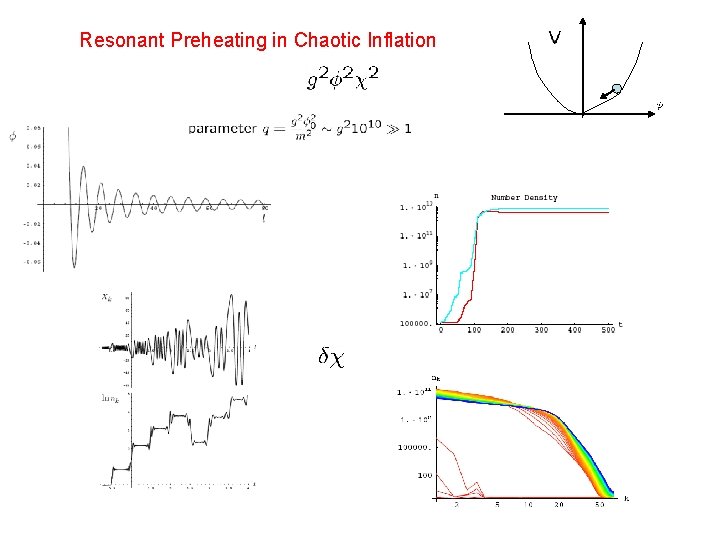
Resonant Preheating in Chaotic Inflation

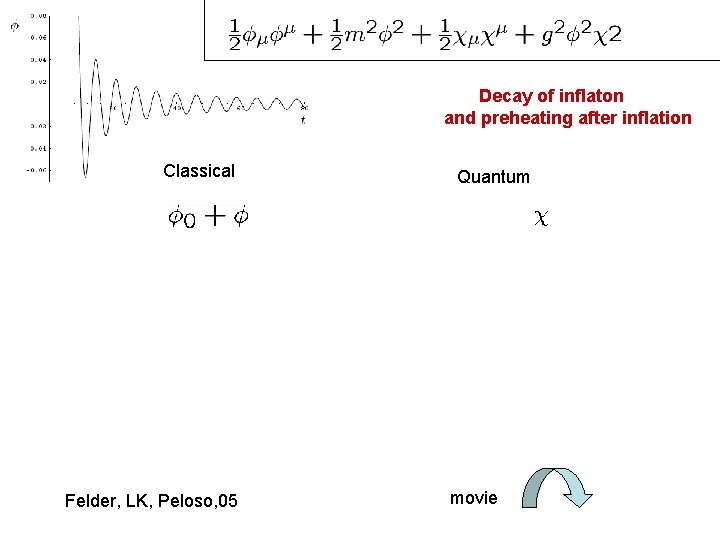
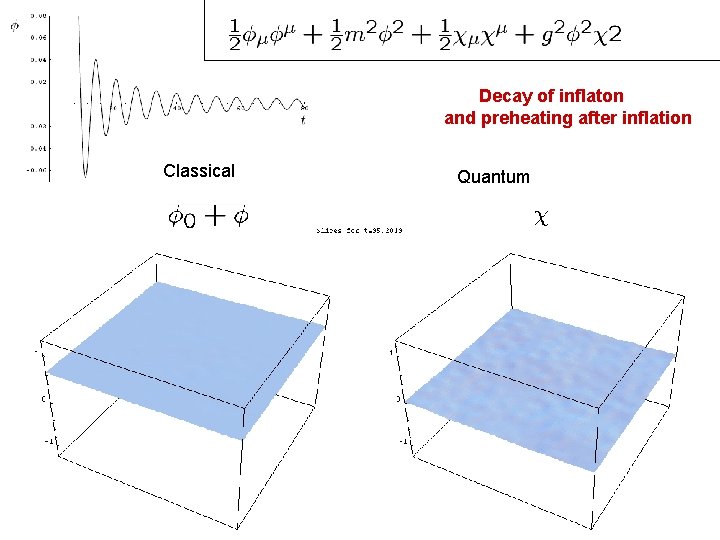
Decay of inflaton and preheating after inflation Classical Felder, LK, Peloso, 05 Quantum movie

Decay of inflaton and preheating after inflation Classical Quantum

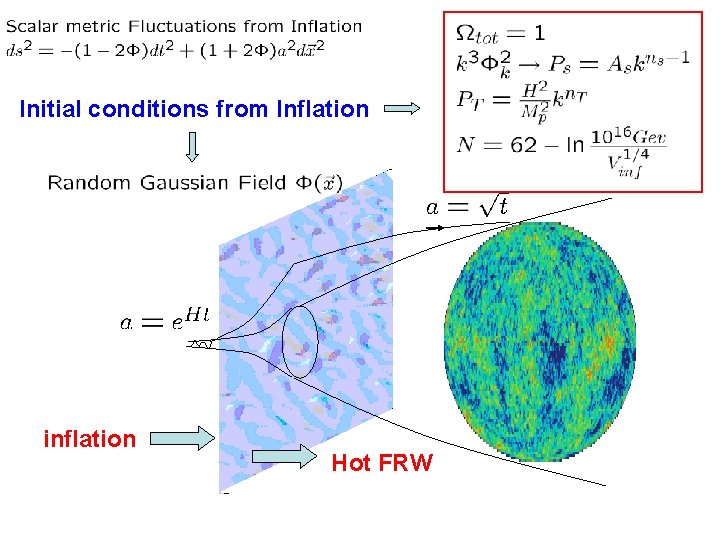
Initial conditions from Inflation inflation Hot FRW

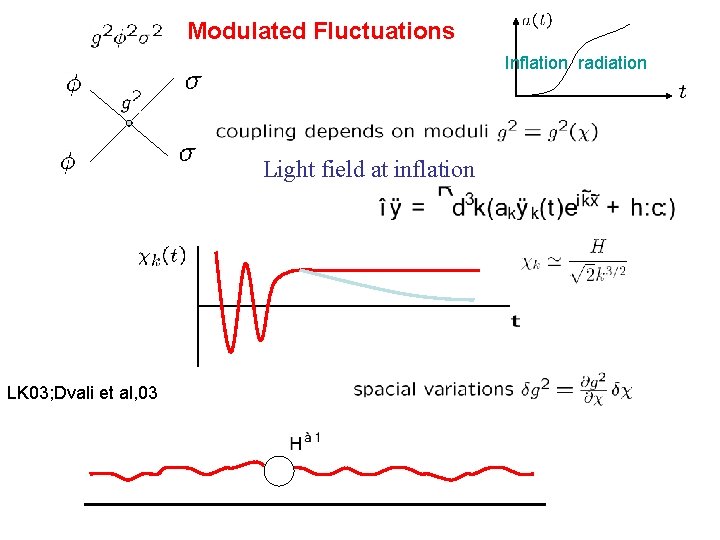
Modulated Fluctuations Inflation radiation Light field at inflation LK 03; Dvali et al, 03

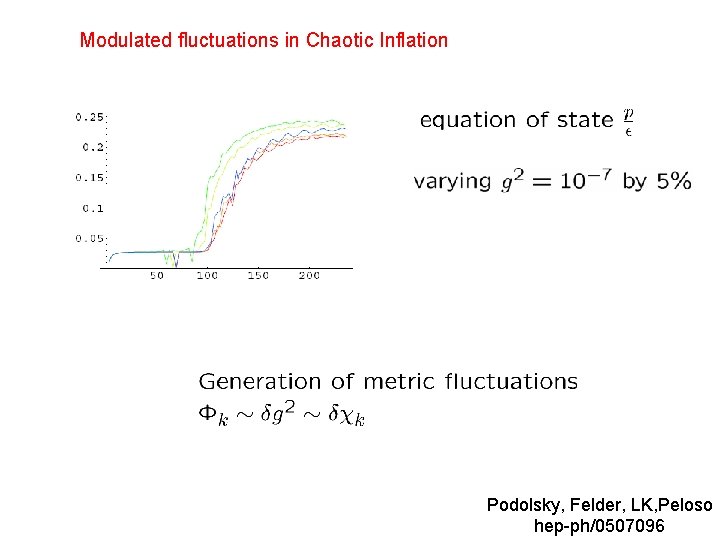
Modulated fluctuations in Chaotic Inflation Podolsky, Felder, LK, Peloso hep-ph/0507096

4 dimensional Inflation predicts No classical inhomogeneities from the past Scale free gaussian fluctuations of all light scalars No vector perturbations Scalar (almost scale free gaussian) metric perturbations Tensor (scale free gaussian) metric perturbations Creation of all SM particles in preheating/thermalization

Inflation in the context of ever changing fundamental theory 1980 -inflation Old Inflation New Inflation Chaotic inflation SUGRA inflation Double Inflation 1990 Extended inflation Hybrid inflation SUSY F-term inflation 2000 Power-law inflation SUSY P-term inflation Racetrack inflation Assisted inflation SUSY D-term inflation Brane inflation Super-natural Inflation K-flation N-flation DBI inflation Tachyon inflation Warped Brane inflation

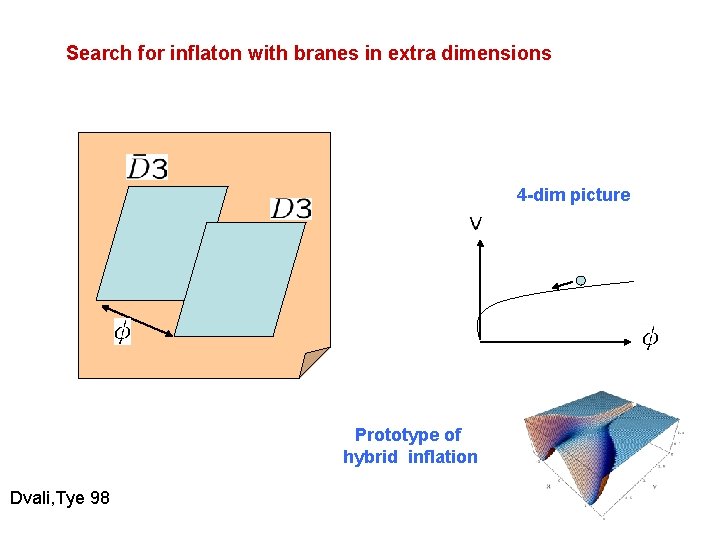
Search for inflaton with branes in extra dimensions 4 -dim picture Prototype of hybrid inflation Dvali, Tye 98

Compactification of inner dimensions with branes Old string theory New phenomenology Strongly warped 5 d geometry Randal, Sundrum 99

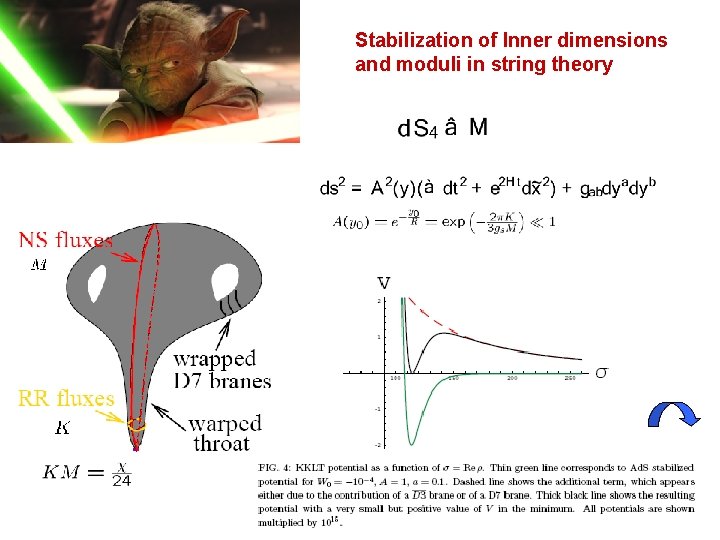
Stabilization of Inner dimensions and moduli in string theory

Realization of String Theory Inflation KKLMMT 03 on the ground of KKLT throat warped geometry Mobile brane Warped brane inflation Conformal coupling problem Realization of warped brane inflation with conformal inflaton modulated fluctuations scalar field associated with angular position at

Realization of String Theory Chaotic Inflation Mobile brane Mukohyama, LK 05 Chaotic inflation

Reheating after String Theory Inflation Barnaby, Burgess, Cline, hep-th/0412095 LK, Yi, hep-th/0507257 Frey, Mazumdar, Myers, hep-th/0508139 Chialva, Shiu, Underwood, hep-th/0508229

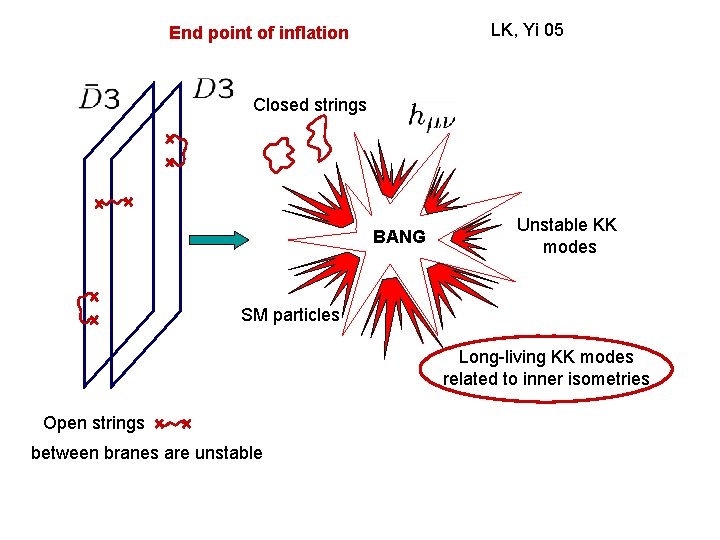
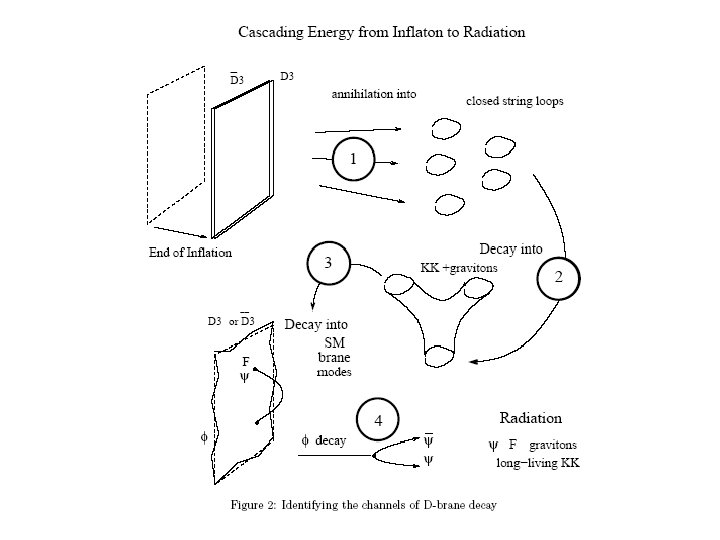
LK, Yi 05 End point of inflation Closed strings BANG Unstable KK modes SM particles Long-living KK modes related to inner isometries Open strings between branes are unstable

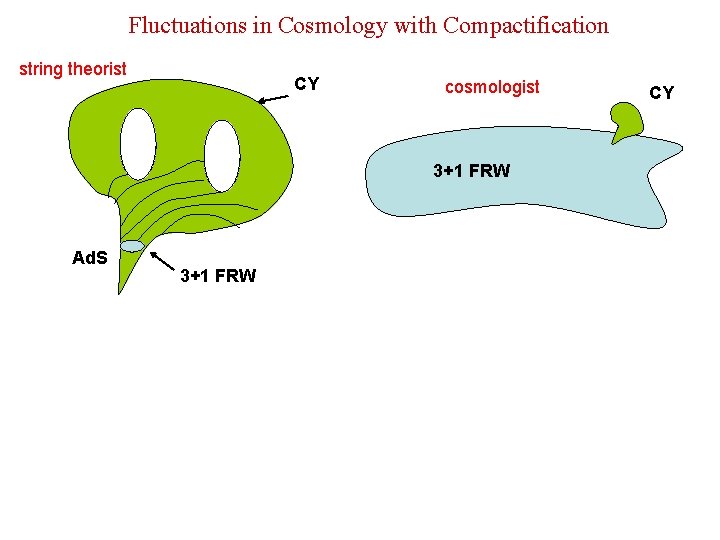
Fluctuations in Cosmology with Compactification string theorist Ad. S CY 3+1 FRW

Fluctuations in Cosmology with Compactification string theorist CY cosmologist 3+1 FRW Ad. S 3+1 FRW CY

Fluctuations in Cosmology with Compactification string theorist CY cosmologist 3+1 FRW Ad. S 3+1 FRW CY +fluctuations Practical cosmologist 3+1 FRW +fluctuations CY

KK story KK particles are thermalized first SM particles are thermalized much later KK from M with isometries are stable No complete decya KK particles freeze out

4 dim Inflation in 10 dim String Theory predicts All what 4 dim inflation predicts Creation of non-SM particles (KK modes) in reheating/thermalization Short-wavelength gravitational radiation Scale free gaussian fluctuations of many light scalars Modulated cosmological fluctuations String theory Cosmic strings

Bottom-up Scanning Inflation R. Bond, C. Contaldi, A. Frolov, L. Kofman T. Souradeep P. Vandrevange

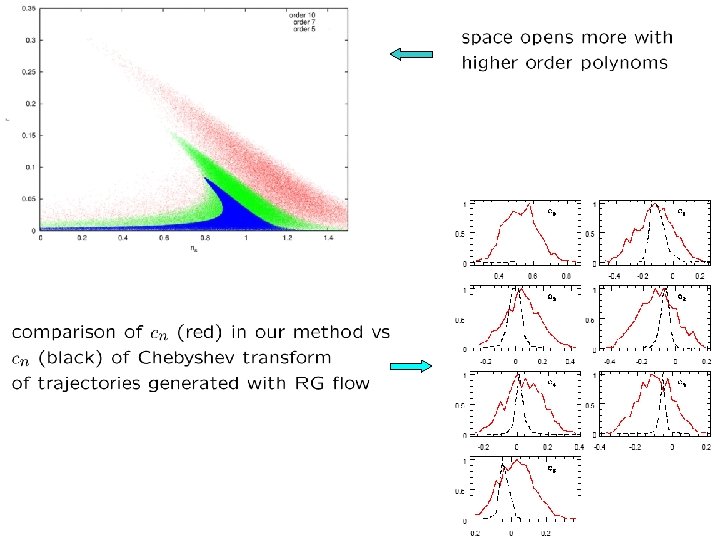
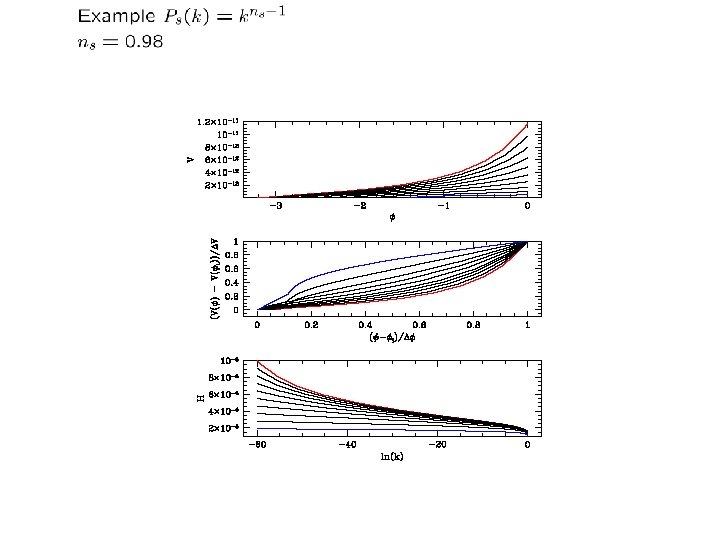
Ensemble of Inflationary trajectories Chebyshev decomposition Space of models opens wide

Observational constraints on trajectories Markov Chain Monte Carlo

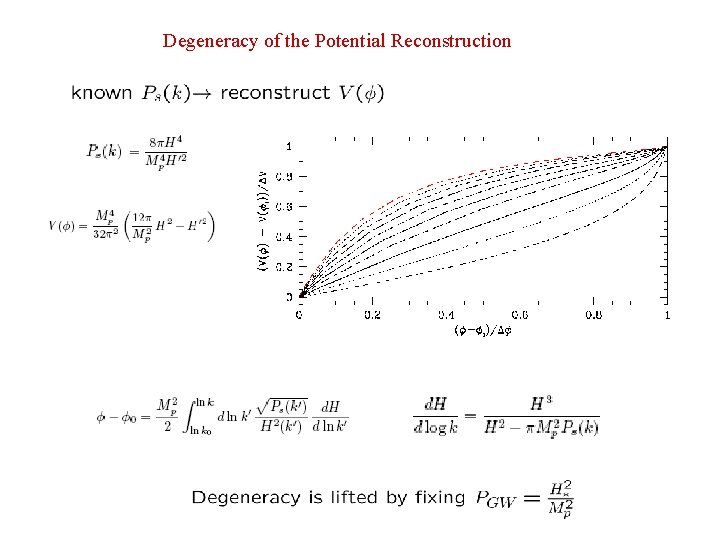
Degeneracy of the Potential Reconstruction

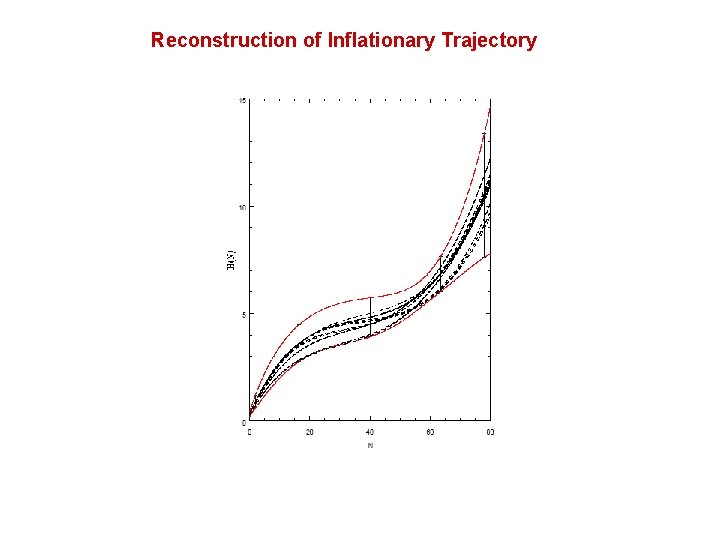
Reconstruction of Inflationary Trajectory

The Parameters of Cosmic Structur Formation Cosmic Numerology: CMBall + LSS, stable & consistent pre-WMAP 1 & post. WMAP 1 (BCP 03), Jun 03 data (BCLP 04), CMBall+CBIpol 04, CMBall+Boom 03+LSS Jul’ 21 05, CMBall Jul 05 LSS=2 d. F, SDSS (weak lensing, cluster abundances); also HST, SN 1 a As = 22 +- 3 x 10 -10 ns =. 95 +-. 02 (. 97 +-. 02 with tensor) (+-. 004 PL 1) At / As < 0. 36 95% CL (+-. 02 PL 2. 5+Spider) dns /dln k = -. 07 +-. 04 to -. 05 +-. 03 (+-. 005 P 1) -. 002 +-. 01 (+Lya Mc. Donald etal 04) (Aiso / As < 0. 3 large scale, < 3 small scale niso = 1. 1+-. 6)