Scanning Gate Microscopy of a Nanostructure inside which

Scanning Gate Microscopy of a Nanostructure inside which electrons interact Axel Freyn, Ioannis Kleftogiannis and Jean-Louis Pichard CEA / IRAMIS Service de Physique de l’Etat Condensé Phys. Rev. Lett. 100, 226802 (2008)

Outline • Part I : The quantum transmission of a nanosystem inside which the electrons interact becomes non local. • Part II : Method for probing electron-electron interactions inside a nanostructure using a scanning gate microscope.

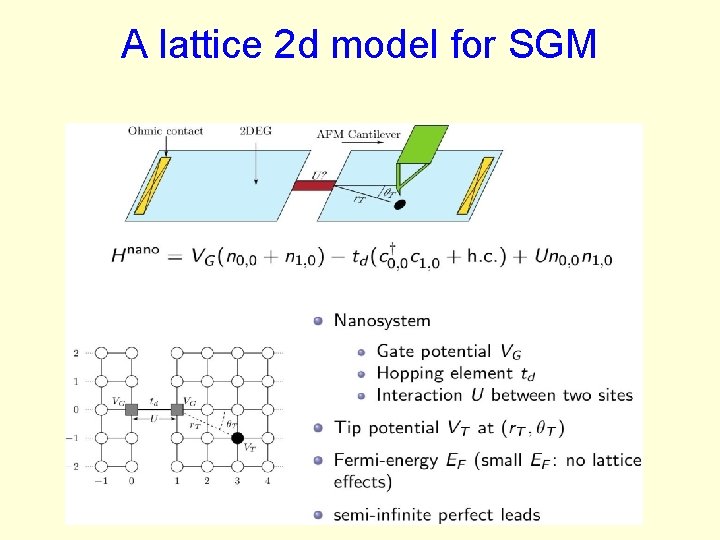
The simplest spinless lattice model with a single nearest neighbor interaction Interacting nanosystem with six parameters • 3 Hopping integrals: ( td , tc, th =1) • Nearest neighbor repulsion: U n 1 no • Gate potential: VG • Filling factor (Fermi energy: EF)

Interacting nanosystem in series with a one body scatterer (attached ring pierced by an Aharonov-Bohm flux) A. Freyn and JLP, Phys. Rev. Lett. 98, 186401 (2007)

Effective nanosystem transmission |ts|2 (Hartree-Fock approximation) Large effect of the AB-flux upon the effective transmission |ts|2 This effect occurs only if the electrons interact inside the nanosystem

The effect of the AB-flux upon the nanosystem effective transmission falls off with the distance LC Decay expected for Friedel oscillations

2 nanosystems in series Y. Asada, A. Freyn and JLP; Eur. Phys. J. B 53, 109 (2006)

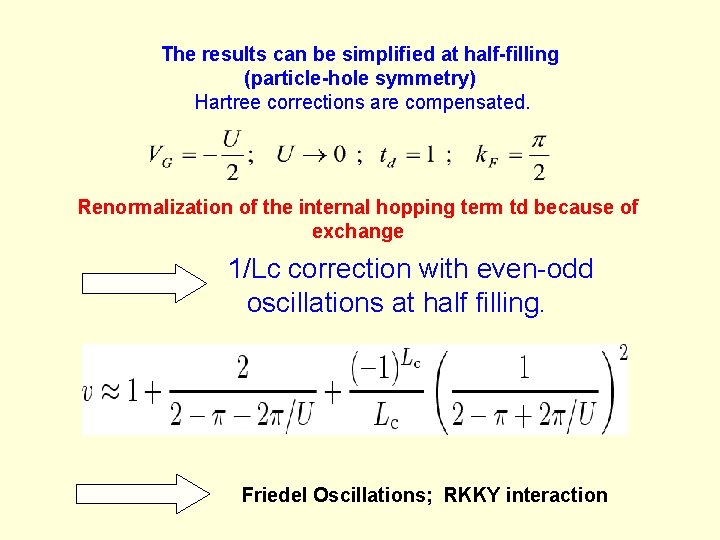
The results can be simplified at half-filling (particle-hole symmetry) Hartree corrections are compensated. Renormalization of the internal hopping term td because of exchange 1/Lc correction with even-odd oscillations at half filling. Friedel Oscillations; RKKY interaction

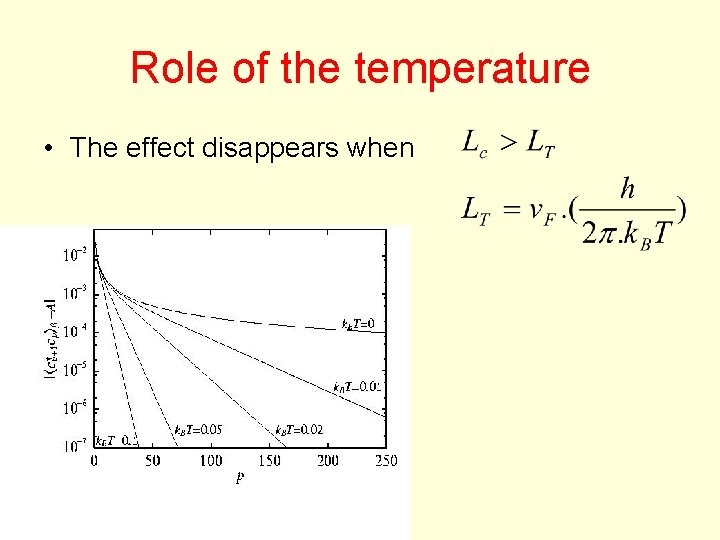
Role of the temperature • The effect disappears when

Origin of the non local transmission (Hartree-Fock theory) • The external scatterer induces Friedel oscillations of the electron density inside the interacting nanosystem • This modifies the Hartree potentials and the Fock corrections inside the nanosystem. • The nanosystem effective transmission can be partly controlled by external scatterers when the electrons interact inside the nanosystem

• To neglect electron-electron interactions outside the nanosystem is not realistic when 1 d wires are attached to it. • This assumption becomes more realistic if one attaches 2 d strips of large enough electron density Scanning gate microscopy

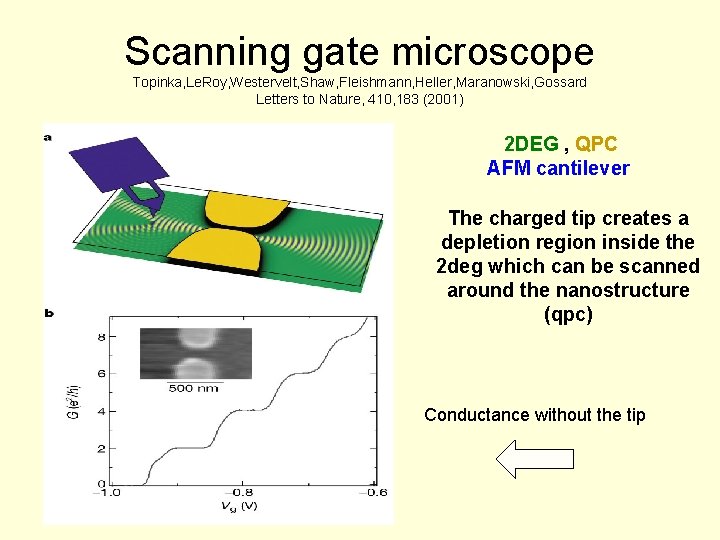
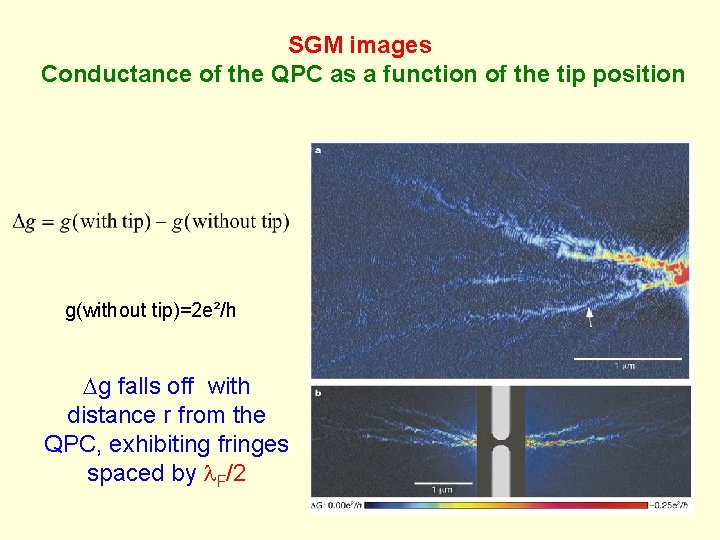
Scanning gate microscope Topinka, Le. Roy, Westervelt, Shaw, Fleishmann, Heller, Maranowski, Gossard Letters to Nature, 410, 183 (2001) 2 DEG , QPC AFM cantilever The charged tip creates a depletion region inside the 2 deg which can be scanned around the nanostructure (qpc) Conductance without the tip

SGM images Conductance of the QPC as a function of the tip position g(without tip)=2 e²/h Dg falls off with distance r from the QPC, exhibiting fringes spaced by l. F/2

The electron-electron interactions inside the QPC can be probed by SGM images • By lateral gates (or additional top gate), one reduces the electron density inside the QPC. This makes the interactions non negligible inside the QPC, [0. 7 (2 e 2 /h) anomaly]. The density remains important and the interactions negligible outside the QPC. • The Friedel oscillations created by the charged tip can modify the effective QPC transmission, if the electrons interact inside the QPC

A lattice 2 d model for SGM

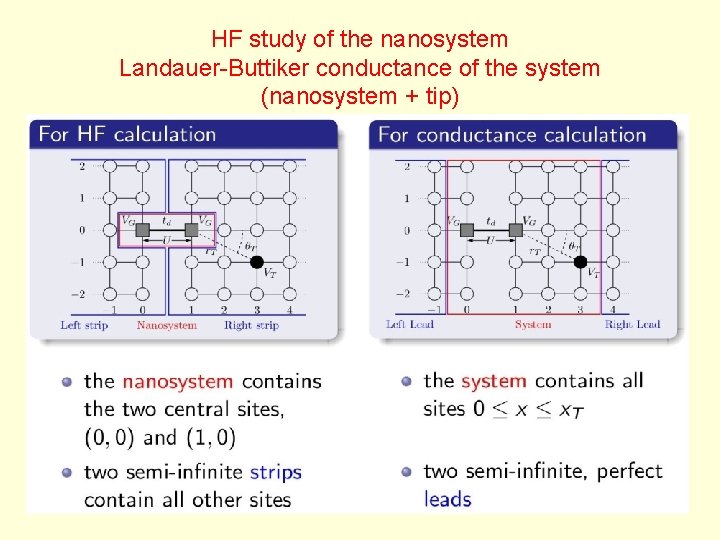
HF study of the nanosystem Landauer-Buttiker conductance of the system (nanosystem + tip)

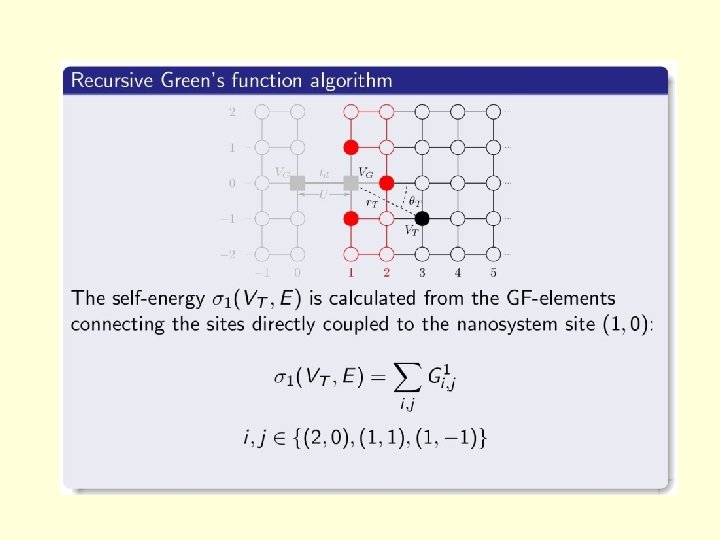
Hartree-Fock theory for the interacting nanosystem coupled to 2 d non interacting strips This self-energy has to be calculated using a recursive method for different positions of the tip and energies E<EF

Self-consistent solution of coupled integral equations

Conductance of the combined system (nanosystem + tip)

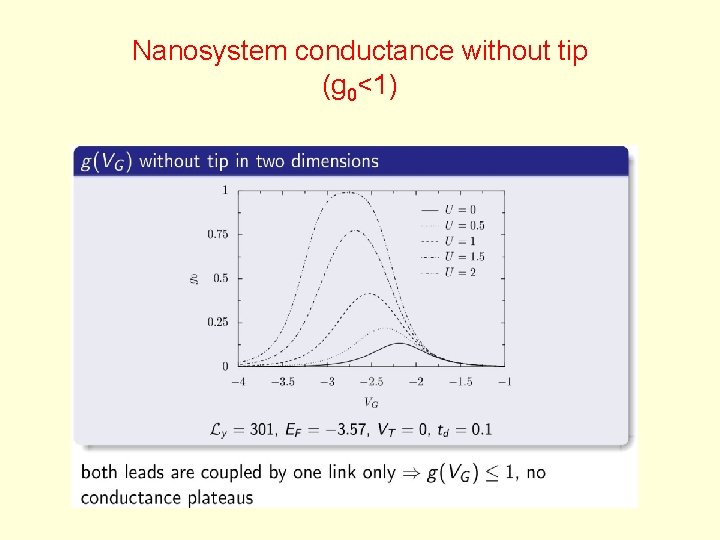
Nanosystem conductance without tip (g 0<1)

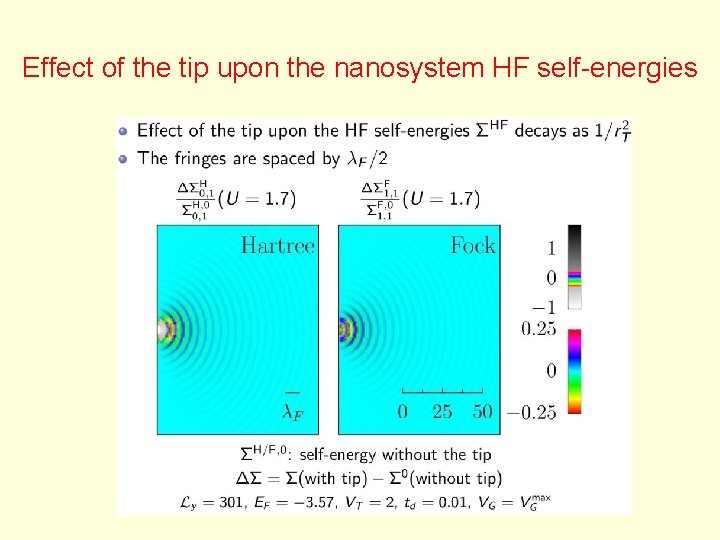
Effect of the tip upon the nanosystem HF self-energies

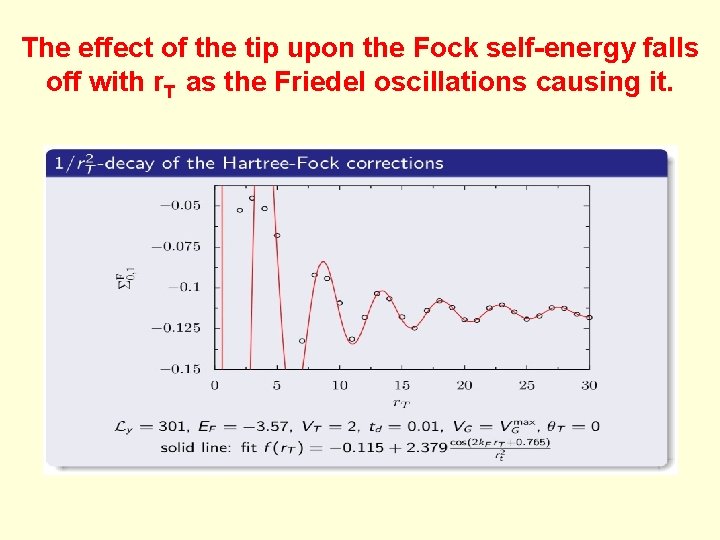
The effect of the tip upon the Fock self-energy falls off with r. T as the Friedel oscillations causing it.

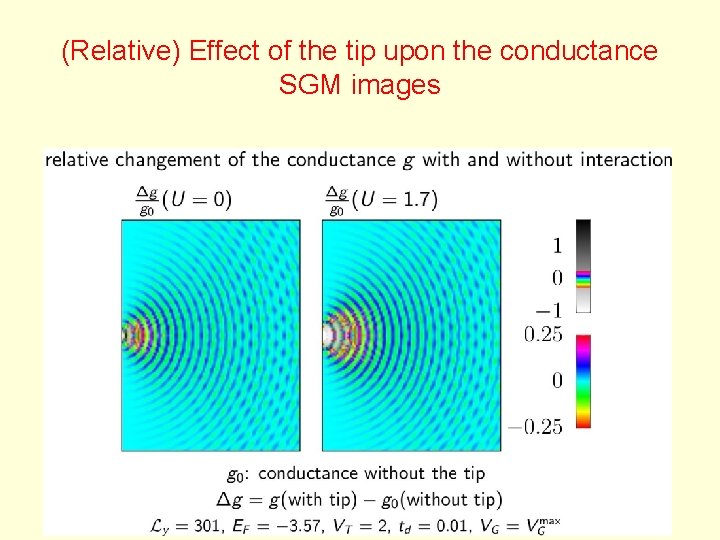
(Relative) Effect of the tip upon the conductance SGM images

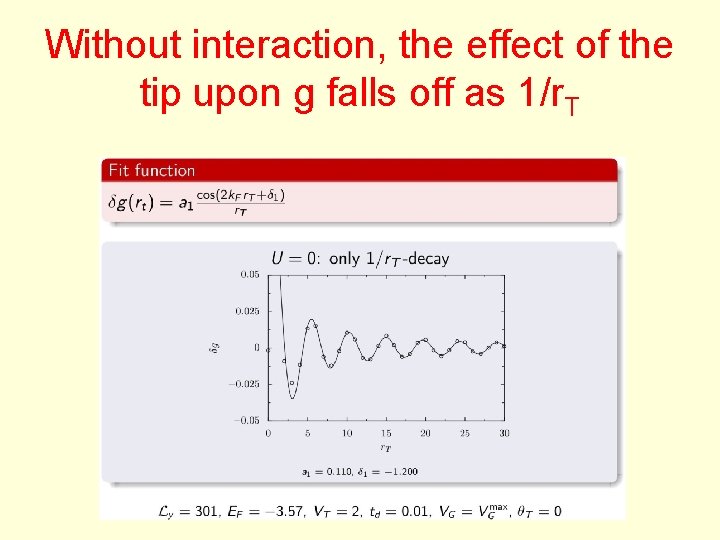
Without interaction, the effect of the tip upon g falls off as 1/r. T

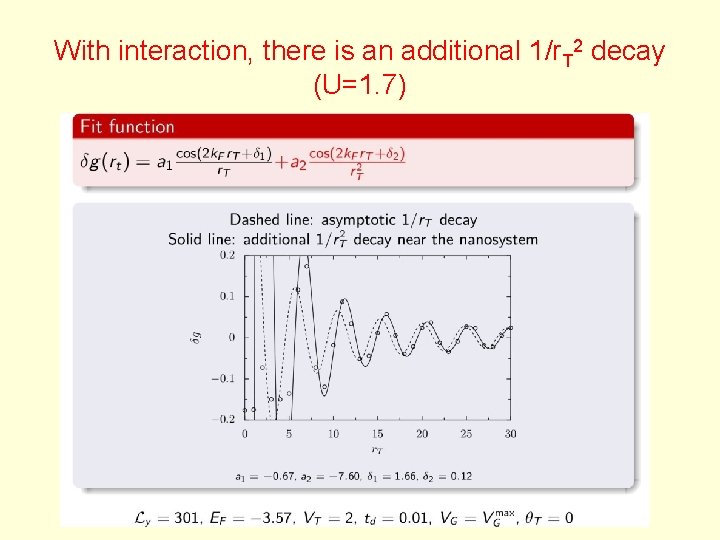
With interaction, there is an additional 1/r. T 2 decay (U=1. 7)

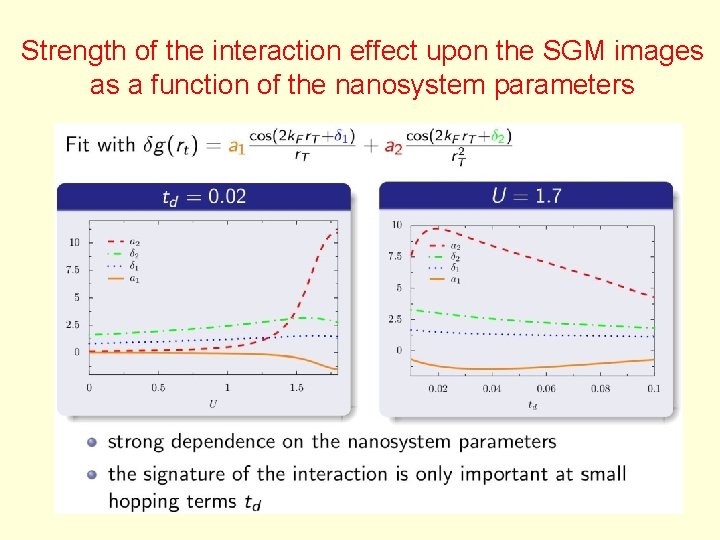
Strength of the interaction effect upon the SGM images as a function of the nanosystem parameters

Summary • The effective transmission can be modified by external scatterers when the electrons interact inside the nanosystem. • This non local effect can be probed using a scanning gate microscope (enhanced fringes near the nanostructure + phase shift of the fringes). • In the HF approximation, the effect is induced by the Friedel (Hartree) or related (exchange) oscillations created by the external scatterers inside the nanosystem. • One can make the effect very large by a suitable choice of the nanosystem parameters. Reducing td enhances the effect. But an orbital Kondo effect (yielded by inversion symmetry) occurs when td goes to 0. • Comparison between HF, DMRG, NRG results…

References • • • R. Molina, D. Weinmann and JLP, Eur. Phys. J. B 48, 243, (2005). Y. Asada, A. Freyn and JLP, Eur. Phys. J. B 53, 109 (2006). A. Freyn and JLP, Phys. Rev. Lett. 98, 186401 (2007). A. Freyn and JLP, Eur. Phys. J. B 58, 279 (2007). A. Freyn, I. Kleftogiannis and JLP, Phys. Rev. Lett. 100, 226802 (2008). • D. Weinmann, R. Jalabert, A. Freyn, G. -L. Ingold and JLP, ar. Xiv: 0803. 2780 (2008).

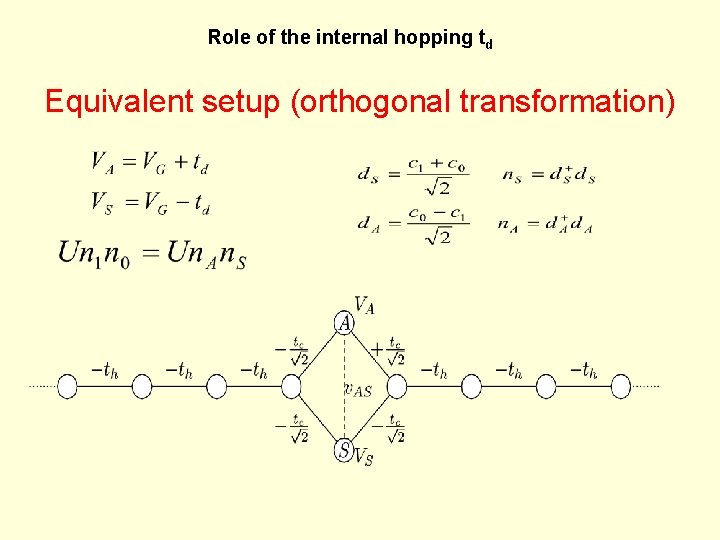
Role of the internal hopping td Equivalent setup (orthogonal transformation)

Hartree-Fock Equations 1. Original basis 2. Transformed basis (v. AS = 0 because of inversion symmetry)