scannerlexical analyzer z scanner z scannerfinite state automaton

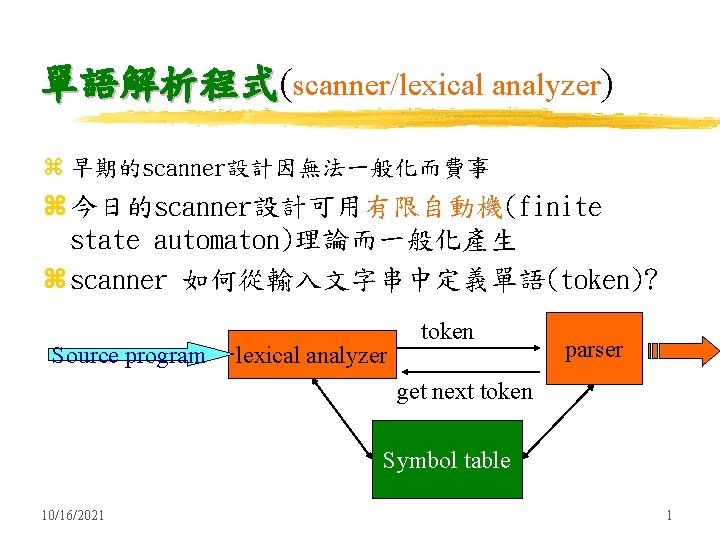
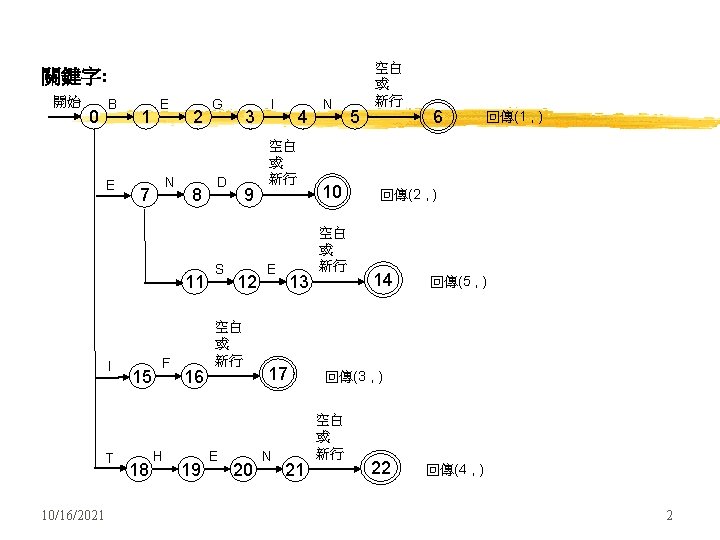
單語解析程式( 單語解析程式 scanner/lexical analyzer) z 早期的scanner設計因無法一般化而費事 z 今日的scanner設計可用有限自動機(finite state automaton)理論而一般化產生 z scanner 如何從輸入文字串中定義單語(token)? Source program lexical analyzer token parser get next token Symbol table 10/16/2021 1

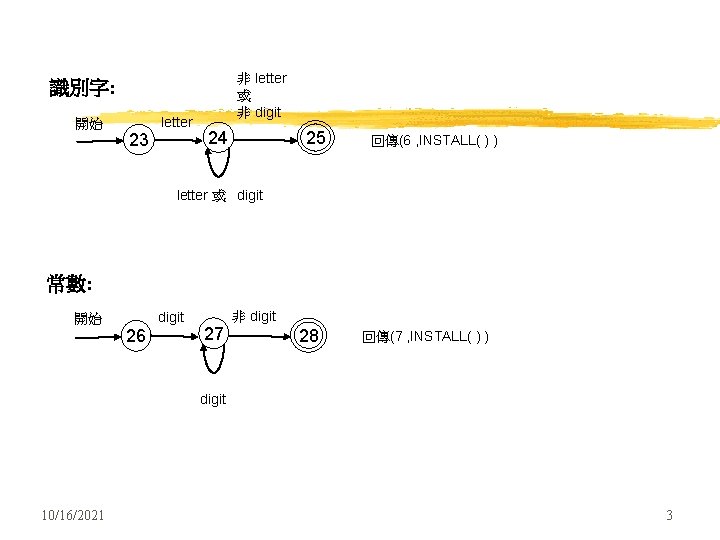
非 letter 或 非 digit 識別字: 開始 letter 23 24 25 回傳(6 , INSTALL( ) ) letter 或 digit 常數: 開始 digit 26 27 非 digit 28 回傳(7 , INSTALL( ) ) digit 10/16/2021 3

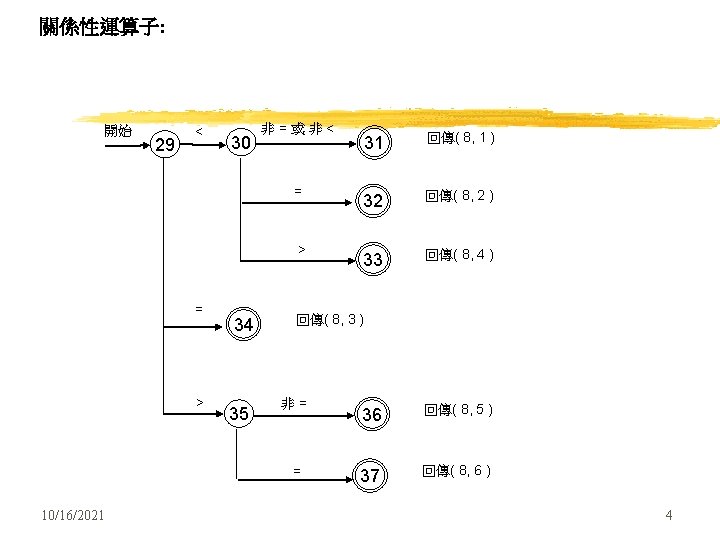
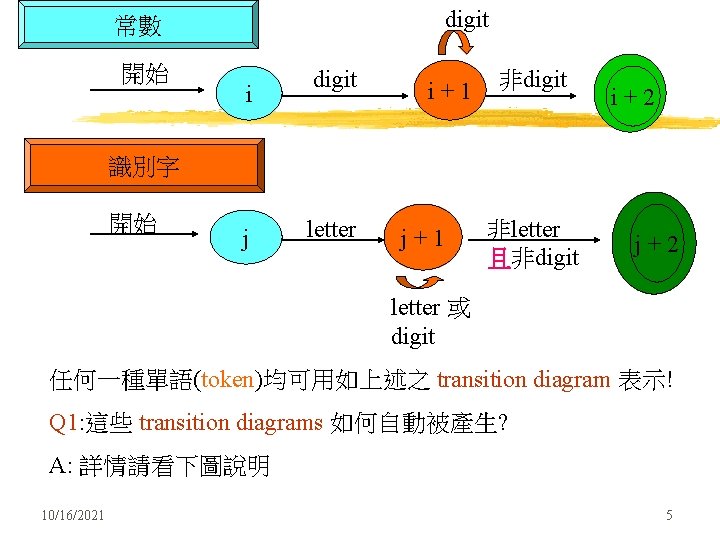
digit 常數 開始 i digit i+1 非digit i+2 識別字 開始 j letter j+1 非letter 且非digit j+2 letter 或 digit 任何一種單語(token)均可用如上述之 transition diagram 表示! Q 1: 這些 transition diagrams 如何自動被產生? A: 詳情請看下圖說明 10/16/2021 5

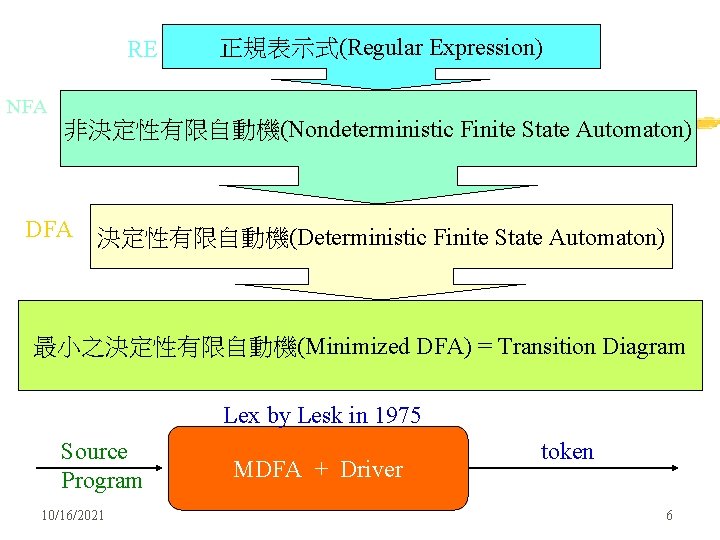
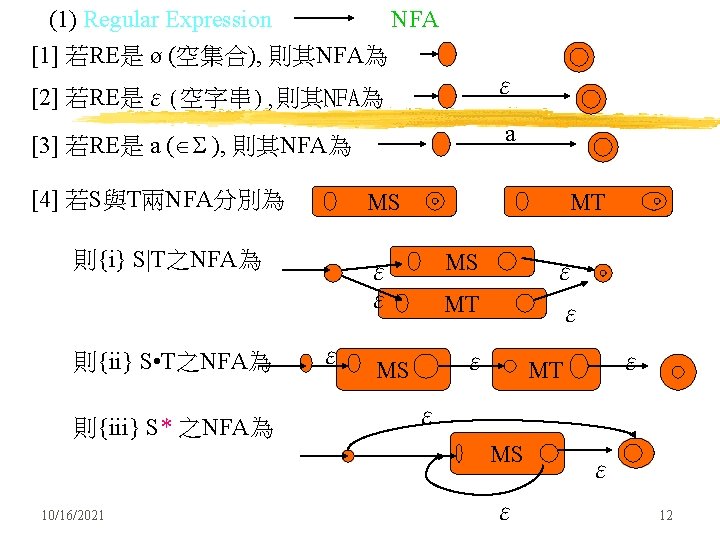
RE NFA 正規表示式(Regular Expression) 非決定性有限自動機(Nondeterministic Finite State Automaton) DFA 決定性有限自動機(Deterministic Finite State Automaton) 最小之決定性有限自動機(Minimized DFA) = Transition Diagram Lex by Lesk in 1975 Source Program 10/16/2021 MDFA + Driver token 6

． ． ． ““ ; /* IGNORE BLANKS */ let return(LET); “*” return(MUL); “=” return (ASSIGN); [a-z. A-Z] [a-z. A-Z 0 -9]* {make entries in tables; return (ID)} (a) %token ASSIGN ID LET MUL ．．． ． statement : LET ID ASSIGN EXPR {．．．} expr : expr MUL expr {$$ = build ( MUL, $1 , $3 ) ; } expr : ID {．．．} ． ． ． (b) 10/16/2021 7

0* , 10* , 01* , 0*1* , (10 | 11)* The languages accepted by finite automata are easily described by simple expressions called regular expressions. The regular expressions over Σ (an alphabet) and the sets that they denote are defined recursively as follows. 1) ∅ is a regular expression and denotes the empty set. 2) ε is a regular expression and denotes the set {ε}. 3) For each a in Σ, a is a regular expression and denotes the set {a}. 4) If r and s are regular expressions denoting the languages R and S, respectively, then ( r | s), (rs), and (r* ) are regular expressions the denote the sets R∪S, RS, and R* , respectively. * ={ε, 10, 11, 1010, 1011, 1110, 1111, . . . } (10 | 11) 10/16/2021 8

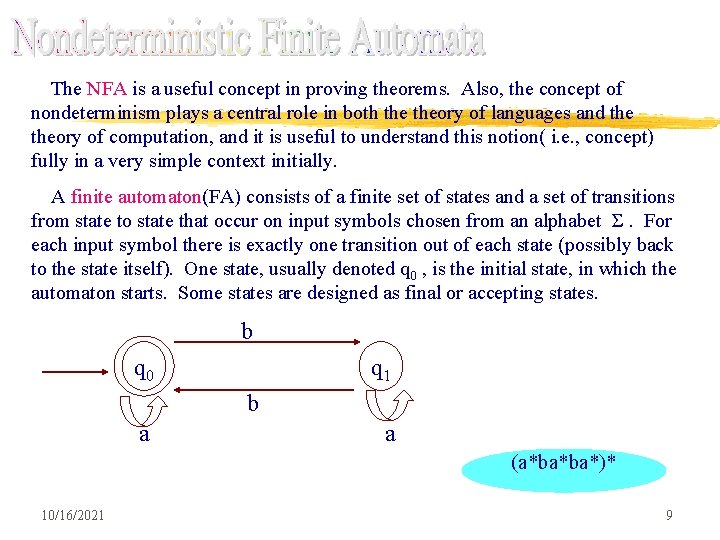
The NFA is a useful concept in proving theorems. Also, the concept of nondeterminism plays a central role in both theory of languages and theory of computation, and it is useful to understand this notion( i. e. , concept) fully in a very simple context initially. A finite automaton(FA) consists of a finite set of states and a set of transitions from state to state that occur on input symbols chosen from an alphabet Σ. For each input symbol there is exactly one transition out of each state (possibly back to the state itself). One state, usually denoted q 0 , is the initial state, in which the automaton starts. Some states are designed as final or accepting states. b q 0 q 1 b a a (a*ba*ba*)* 10/16/2021 9

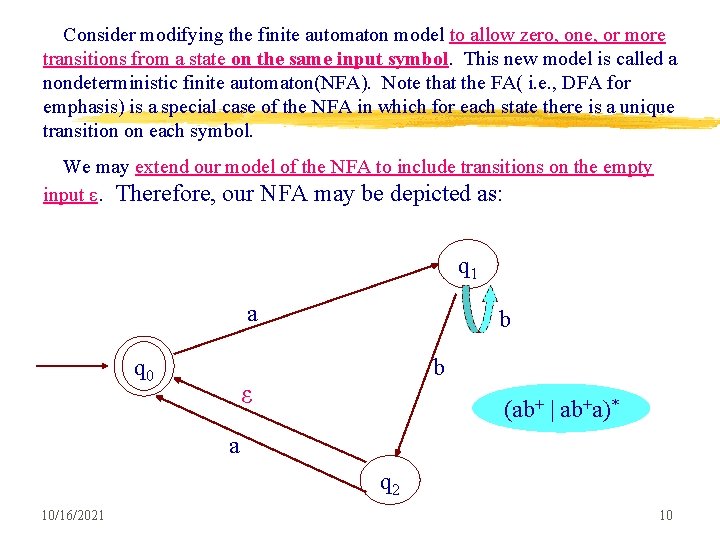
Consider modifying the finite automaton model to allow zero, one, or more transitions from a state on the same input symbol. This new model is called a nondeterministic finite automaton(NFA). Note that the FA( i. e. , DFA for emphasis) is a special case of the NFA in which for each state there is a unique transition on each symbol. We may extend our model of the NFA to include transitions on the empty input ε. Therefore, our NFA may be depicted as: q 1 a q 0 b b ε (ab+ | ab+a)* a q 2 10/16/2021 10

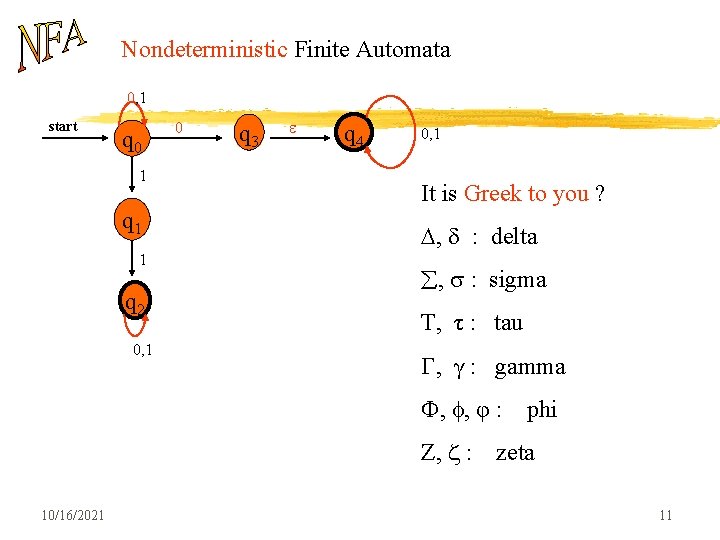
Nondeterministic Finite Automata 0, 1 start q 0 1 q 1 1 q 2 0, 1 0 q 3 q 4 0, 1 It is Greek to you ? D, : delta , : sigma T, τ : tau , γ : gamma , , φ : Z, : 10/16/2021 phi zeta 11

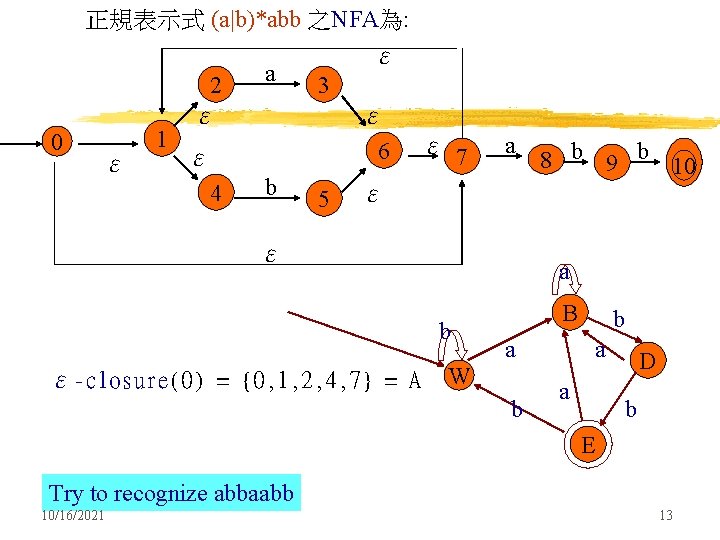
正規表示式 (a|b)*abb 之NFA為: ε a 2 3 ε ε 1 0 ε 6 ε 7 ε b 4 5 ε a b ε-closure(0) = {0, 1, 2, 4, 7} = A 8 b 9 b 10 B a W b b a a D b E Try to recognize abbaabb 10/16/2021 13

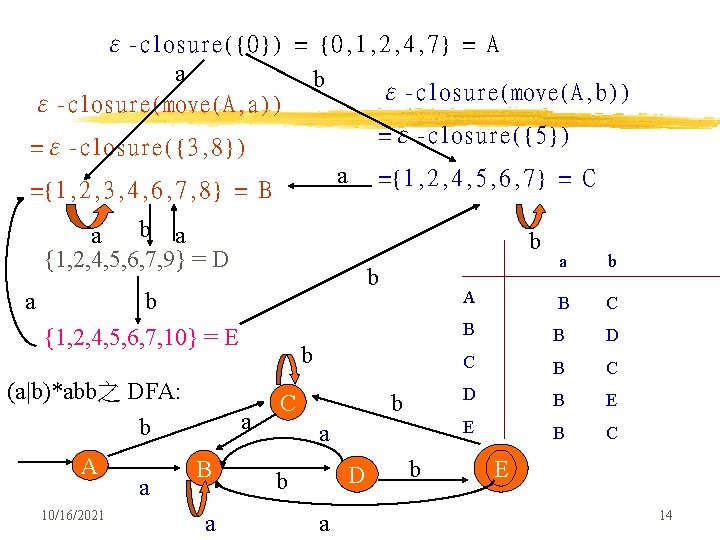
ε-closure({0}) = {0, 1, 2, 4, 7} = A a b ε-closure(move(A, b)) ε-closure(move(A, a)) =ε-closure({5}) =ε-closure({3, 8}) a ={1, 2, 3, 4, 6, 7, 8} = B ={1, 2, 4, 5, 6, 7} = C b a a {1, 2, 4, 5, 6, 7, 9} = D a b b b {1, 2, 4, 5, 6, 7, 10} = E b (a|b)*abb之 DFA: a b A 10/16/2021 a B a C b a D b a b A B C B B D C B C D B E E B C E 14

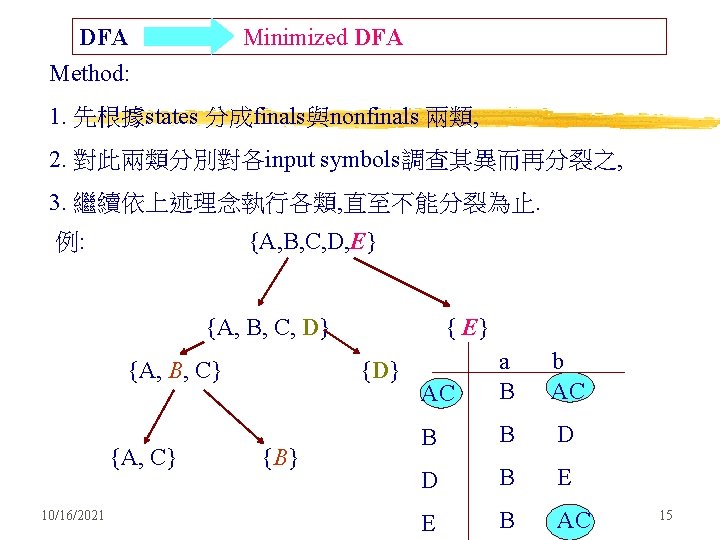
DFA Method: Minimized DFA 1. 先根據states 分成finals與nonfinals 兩類, 2. 對此兩類分別對各input symbols調查其異而再分裂之, 3. 繼續依上述理念執行各類, 直至不能分裂為止. {A, B, C, D, E} 例: {A, B, C, D} {A, B, C} {A, C} 10/16/2021 { E} {D} {B} AC a B b AC B B D D B E E B AC 15

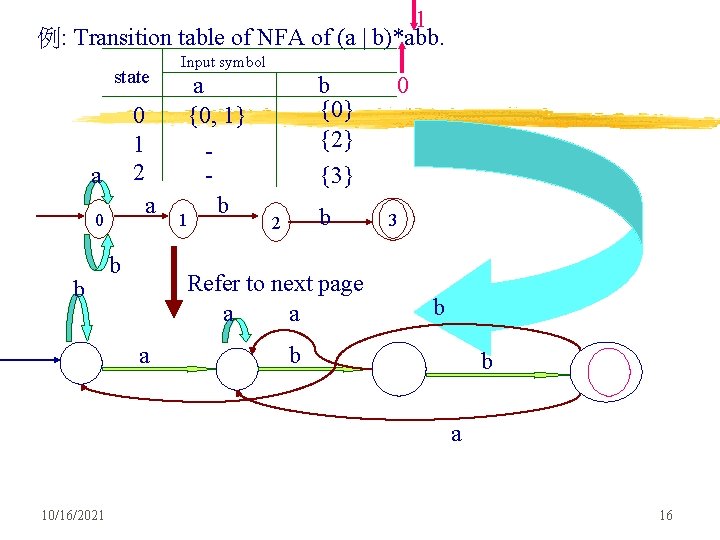
1 例: Transition table of NFA of (a | b)*abb. state 0 1 2 a b a {0, 1} b {0} {2} a 0 Input symbol b 1 {3} b b 2 Refer to next page a a a 0 3 b b b a 10/16/2021 16

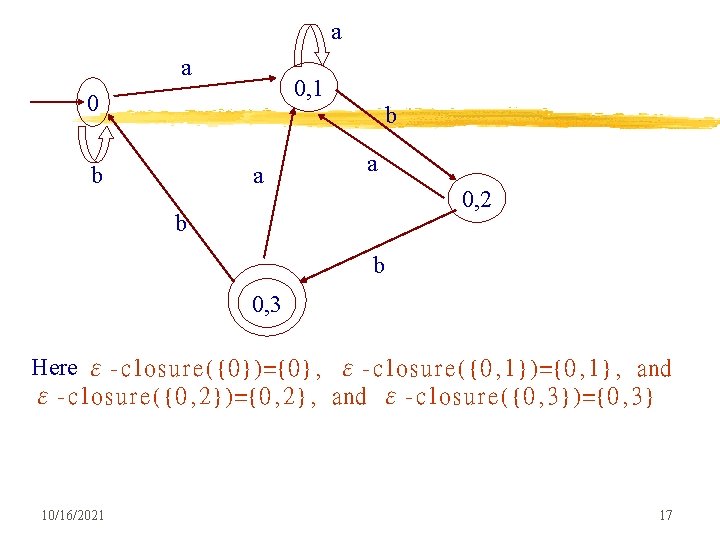
a a 0, 1 0 b b a a 0, 2 b b 0, 3 Here ε-closure({0})={0}, ε-closure({0, 1})={0, 1}, and ε-closure({0, 2})={0, 2}, and ε-closure({0, 3})={0, 3} 10/16/2021 17

Alphabets: An Alphabet is a finite set of symbols. We will usually use to denote the alphabet of input symbols or “terminal characters. ” String: A String (or “sentence” or “word”) is a finite sequence of symbols. The set + : The set of all strings over of length 1 or more. The length of x is |x|. The empty string ; | | = 0 * Concatenation xy or x·y. x = x * x 2 = xx : the set of all strings over of length 0 or more. * { } x is a Prefix of y if there exists a z such that y = xz 10/16/2021 x is a Proper Prefix of y if x is a prefix of y and z y. 18

A Language is some subset of * . Terminals are members of . Another set of symbols (alphabet) are the non-terminals (or variables or syntactic categories) which represent strings of terminals. Vocabulary symbols are terminals or non-terminals. Concatenation of languages L · M = {xy| x L, y M} Li = concatenation of L i times, L 0 = { } L M = {x| x L or x M} The closure of L is L* = i=0 Li = L 0 L 1 L 2 . . . The positive closure of L is L+. 10/16/2021 19

Introduction to Automata Theorem Definitions : An ALPHABET is a finite set of symbols. . We will usually use to denote the alphabet of input symbols or "terminal characters". A STRING is a finite sequence of symbols. A LANGUAGE is some subset of *. Any set of strings accepted by a finite automata is said to be REGULAR. A RECOGNIZER is a machine (system) with a finite description that can accept a terminal string for some grammar and determine whether the string is in the language accepted by the grammar. 10/16/2021 20

Pumping Lemma for Regular Sets Let L be a regular set, then there exists a constant p>0 depending on L such that for every w L where |w| p, w=xyz where 0< |y| p ==> xyk z L for all k 0. Pf: Let M be a finite automaton that accepts L. Let p be the number of states in M. Select w L such that |w| p, then w can be written as a 1 a 2 a 3. . . an-1 an s 0 s 1 s 2 sn-1 sn Since n+1>p, not all of the states can be unique. Let si = sj for some i<j i+p, now let x = a 1 a 2. . . ai , y = ai+1. . . aj , z = aj+1. . . an. Now we can delete y from w or insert y any number of times and we will still go from the start to final state. So xyk z L for every k 0. QED. 10/16/2021 21

Qz 1: Prove L={ 0 n 1 n| n 1} is NOT regular Pf: Assume L is regular. Pick a “large enough” string in L, say w = 0 p 1 p. Now, show no substring y of w can be pumped. One of the following must be true. (w = 0 p 1 p = xyz) (1) y = 0 i for some i 1 but xy 2 z = 0 p+i 1 p L (2) y = 1 i for some i 1 but xy 2 z = 0 p 1 p+i L (3) y = 0 i 1 j for some i, j 1 but xy 2 z = 0 p-i 0 i 1 j 1 p-j L p 1 j 0 i 1 p 0 Therefore, L is NOT regular. QED. n steps 0 1 10/16/2021 0 1 22

Qz 2: Prove L={ 0 p| p is a prime number} is NOT regular Pf: Assume L is regular. [thus any string of L is pumpable] Let w = xyz where x=ap, y=aq , z=ar, p, r 0, q> 0, then 0 p+nq+r L for each n 0, that is p+nq+r is prime for each n 0. But this is impossible, since let n = p+2 q+r+2, then p+nq+r = (q+1)(p+2 q+r) which is a product of two natural numbers each greater than 1. So, if n=p+2 q+r+2, then p+nq+r is NOT prime. Therefore, it is controversy to the assumption of w L for each n 0. 10/16/2021 QED. 23

Theorem: Let L be a set accepted by a nondeterministic finite state automaton. Then there exists a deterministic finite state automaton that accepts L. The feeling of pumping x z Def: y DFA: M=(K, , , S 0, F) where K=set of states, = set of alphabet, S 0 K, the start state. F K, set of final states, and 10/16/2021 : k * K, the transition function 24

Exercises: 1. Construct minimum-state DFA’s for the following regular expressions. (a) (a|b)*a(a|b) 2. Reduce the following NFA to a minimal DFA. F is the only final state. ｜ + ( ) * -----｜--------------S ｜ A B A A ｜ D D B B ｜ A B C E C ｜ D F A D ｜ E C E ｜ C F D F F ｜ B 10/16/2021 25

I. Define the following: ( a ) A grammar; ( b) Four types of grammars; ( c ) Four types of languages; II. Let= { a, b} and let L = { | } ( a ) Show that L is a context-free language; ( b ) Show that L is not a regular language. III. Let ={ a , b}. Give an automaton each which accept the following languages. (a) = ; (b)={ } 10/16/2021 26

IV. Find the languages accepted by the following automata ={ a , b } (a) (b) V. Define the following terms: ( a ) an algorithm; ( b) a procedure; ( c ) regular operations; VI. Let A={ }be an automaton. Let the relation R defined on by if and only if where. Show that ( a ) R is an equivalence relation. ( b )Show that R is right invariant. 10/16/2021 27