Scanner 2015 03 16 Front End Source code

Scanner 2015. 03. 16

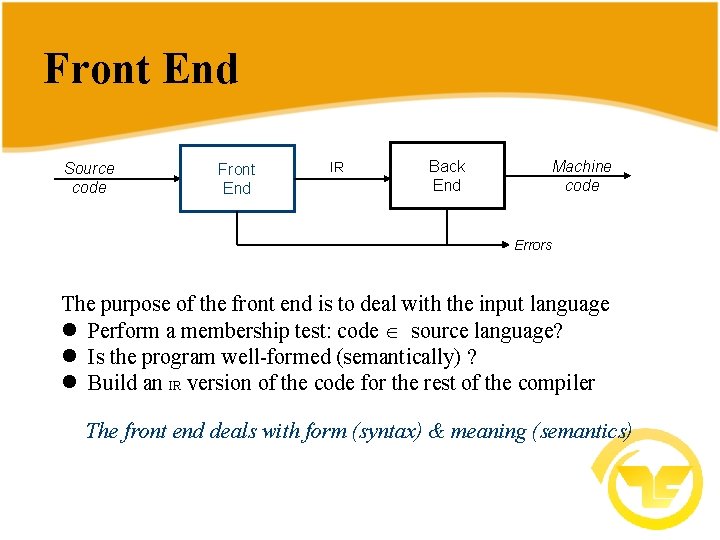
Front End Source code Front End IR Back End Machine code Errors The purpose of the front end is to deal with the input language l Perform a membership test: code source language? l Is the program well-formed (semantically) ? l Build an IR version of the code for the rest of the compiler The front end deals with form (syntax) & meaning (semantics)

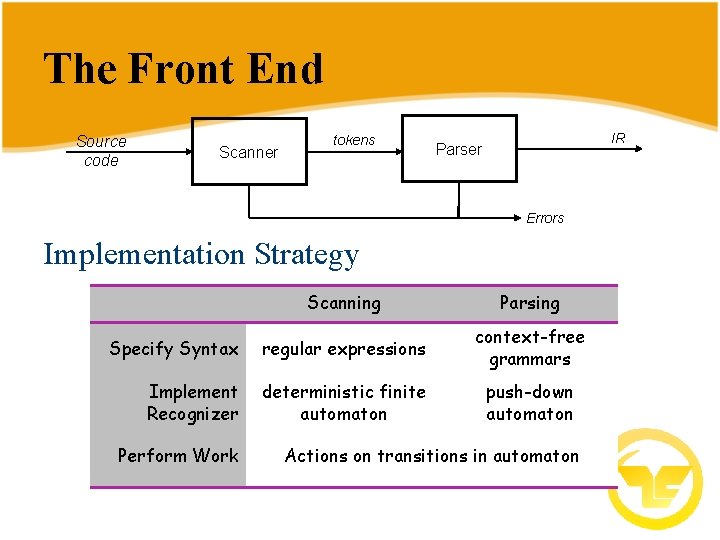
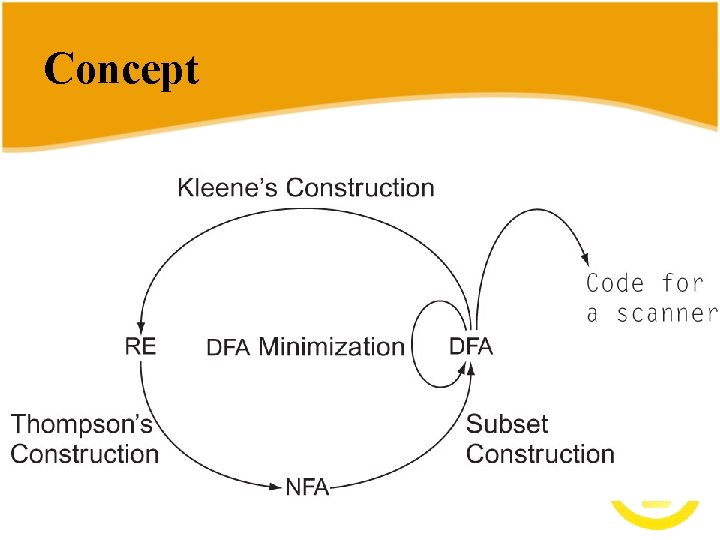
The Front End Source code Scanner tokens IR Parser Errors Implementation Strategy Scanning Parsing Specify Syntax regular expressions context-free grammars Implement Recognizer deterministic finite automaton push-down automaton Perform Work Actions on transitions in automaton

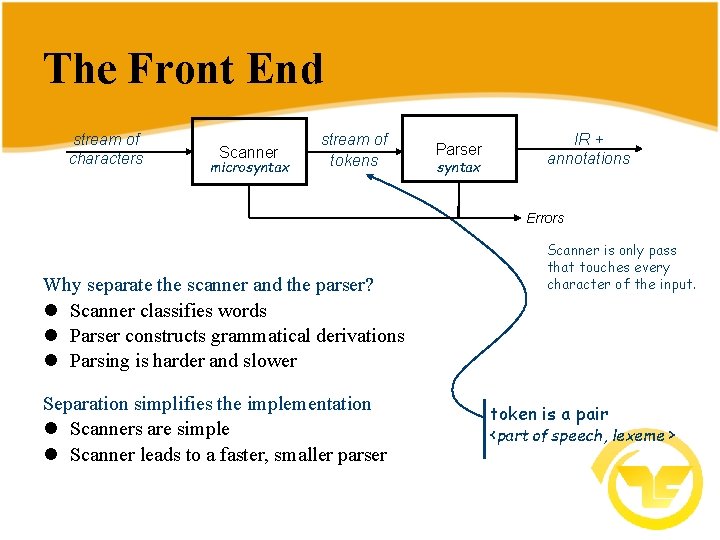
The Front End stream of characters Scanner microsyntax stream of tokens Parser syntax IR + annotations Errors Why separate the scanner and the parser? l Scanner classifies words l Parser constructs grammatical derivations l Parsing is harder and slower Separation simplifies the implementation l Scanners are simple l Scanner leads to a faster, smaller parser Scanner is only pass that touches every character of the input. token is a pair <part of speech, lexeme >

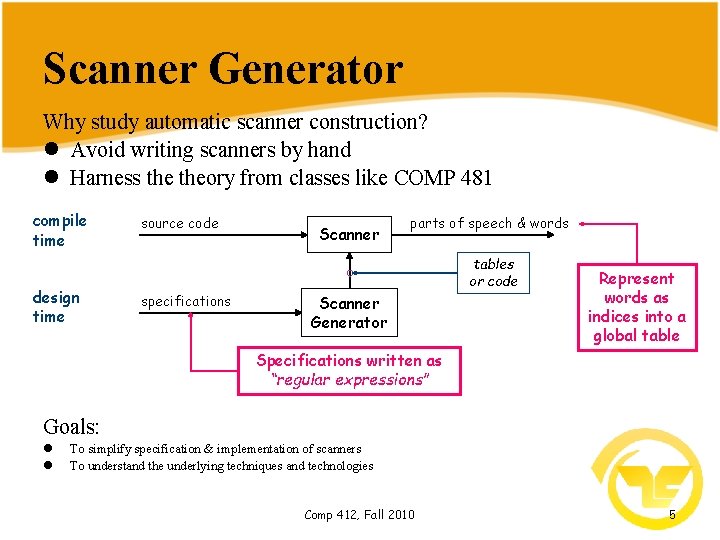
Scanner Generator Why study automatic scanner construction? l Avoid writing scanners by hand l Harness theory from classes like COMP 481 compile time design time source code Scanner parts of speech & words tables or code specifications Scanner Generator Represent words as indices into a global table Specifications written as “regular expressions” Goals: l l To simplify specification & implementation of scanners To understand the underlying techniques and technologies Comp 412, Fall 2010 5

Strings and Languages l Alphabet n An alphabet is a finite set of symbols (characters) l String n A string is a finite sequence of symbols from u s denotes the length of string s u denotes the empty string, thus = 0 l Language n A language is a countable set of strings over some fixed alphabet u. Abstract Language Φ u{ε}

String Operations l Concatenation (連接) n The concatenation of two strings x and y is denoted by xy l Identity (單位元素) n The empty string is the identity under concatenation. n s=s =s l Exponentiation n Define s 0 = si = si-1 s for i > 0 n By Define s 1 = s s 2 = ss

Language Operations l Union L M = { s s L or s M } l Concatenation L M = { xy x L and y M} l Exponentiation L 0 = { } Li = Li-1 L l Kleene closure (封閉包) L* = ∪i=0, …, Li l Positive closure L+ = ∪i=1, …, Li

Regular Expressions l Regular Expressions n A convenient means of specifying certain simple sets of strings. n We use regular expressions to define structures of tokens. n Tokens are built from symbols of a finite vocabulary. l Regular Sets n The sets of strings defined by regular expressions.

Regular Expressions l Basis symbols: n is a regular expression denoting language L( ) = { } n a is a regular expression denoting L(a) = {a} l If r and s are regular expressions denoting languages L(r) and M(s) respectively, then n r s is a regular expression denoting L(r) M(s) n rs is a regular expression denoting L(r)M(s) n r* is a regular expression denoting L(r)* n (r) is a regular expression denoting L(r) l A language defined by a regular expression is called a regular set.

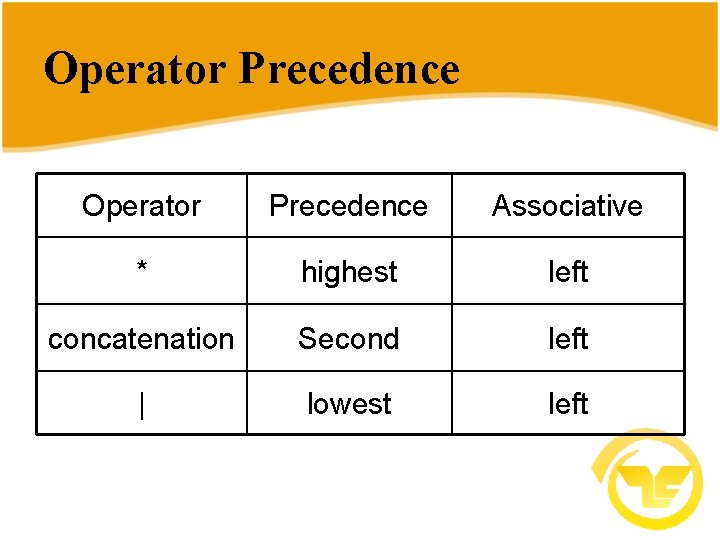
Operator Precedence Associative * highest left concatenation Second left | lowest left

Algebraic Laws for Regular Expressions Law r|s=s|r Description | is commutative r | ( s | t ) = ( r | s ) | t | is associative r(st) = (rs)t r(s|t) = rs | rt (s|t)r = sr | tr concatenation is associative concatenation distributes over | εr = rε = r ε is the identity for concatenation r* = ( r |ε)* ε is guaranteed in a closure r** = r* * is idempotent

Examples of Regular Expressions Identifiers: Letter (a|b|c| … |z|A|B|C| … |Z) Digit (0|1|2| … |9) Identifier Letter ( Letter | Digit )* Numbers: shorthand for (a|b|c| … |z|A|B|C| … |Z) ((a|b|c| … |z|A|B|C| … |Z) | (0|1|2| … |9))* Integer (+|-| ) (0| (1|2|3| … |9)(Digit *) ) Decimal Integer. Digit * Real ( Integer | Decimal ) E (+|-| ) Digit * Complex ( Real , Real ) Numbers can get much more complicated! Using symbolic names does not imply recursion underlining indicates a letter in the input stream 13

Finite Automata l Finite Automata are recognizers. n FA simply say “Yes” or “No” about each possible input string. n A FA can be used to recognize the tokens specified by a regular expression n Use FA to design of a Lexical Analyzer Generator l Two kind of the Finite Automata n Nondeterministic finite automata (NFA) n Deterministic finite automata (DFA) l Both DFA and NFA are capable of recognizing the same languages.

NFA Definitions l NFA = { S, , , s 0, F } n A finite set of states S n A set of input symbols Σ uinput alphabet, ε is not in Σ n A transition function u : S S n A special start state s 0 n A set of final states F, F S (accepting states)

Transition Graph for FA is a state is a transition is a the start state is a final state

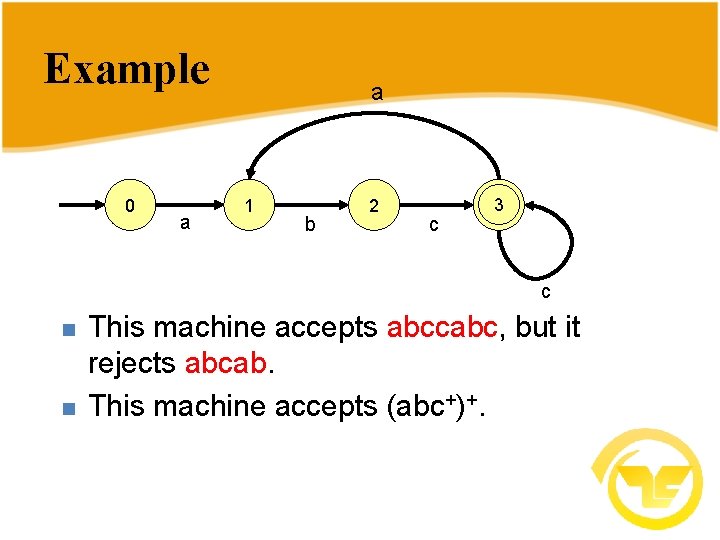
Example 0 a a 1 b 2 c 3 c n n This machine accepts abccabc, but it rejects abcab. This machine accepts (abc+)+.

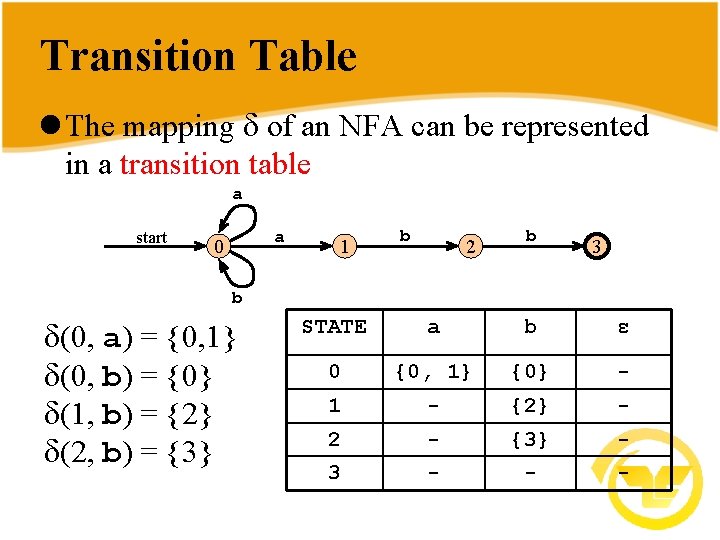
Transition Table l The mapping of an NFA can be represented in a transition table a start a 0 1 b 2 b 3 b (0, a) = {0, 1} (0, b) = {0} (1, b) = {2} (2, b) = {3} STATE a b ε 0 {0, 1} {0} - 1 - {2} - 2 - {3} - 3 - - -

DFA l DFA is a special case of an NFA n There are no moves on input ε n For each state s and input symbol a, there is exactly one edge out of s labeled a. l Both DFA and NFA are capable of recognizing the same languages.

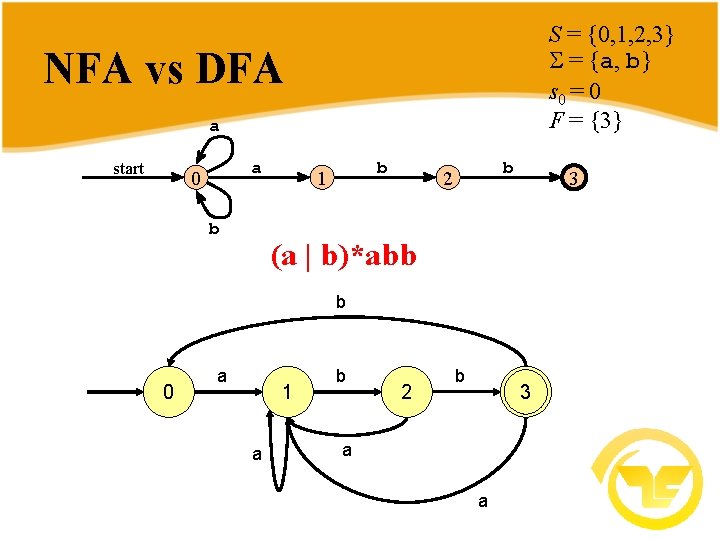
S = {0, 1, 2, 3} = {a, b} s 0 = 0 F = {3} NFA vs DFA a start a 0 b b 1 b 2 3 (a | b)*abb b 0 a 1 a b 2 b 3 a a

Concept