Scan Conversion 2001 1 10 Graphics Lab Contents

Scan Conversion 2001. 1. 10 Graphics Lab. 김성남

Contents • • • Scene Display What is Scan Conversion? Line Drawing Algorithms Circle Algorithm Filled-Area Primitives - Scan-Line Fill Algorithm - Boundary Fill Algorithm - Flood-Fill Algorithm - Inside-Outside Test

Scene Display • Scene Display 무수한 점들로 구성된 image → 제한된 pixel의 집합인 H/W Device(monitor)에 어떻게 표시할 것인가? • Scene Display 방법 - pixel arrays → frame buffer 에 load - basic geometric structures → pixel patterns 으로 scan convert

What is Scan Conversion? • 정의 Image를 display하기위해 CRT등 H/W Device를 scanning 할때 display하고자하는 image에 가장 근사하게(approximately) 대응되는 pixel을 convert 하는 방법 * Graphics System, Package에 따라 다양하다. • Constraint - Digital Device(raster graphics system)

What is Scan Conversion? • Assumption pixel position : X축 : Scan line number Y축 : Column number Scan Line 4 Number 3 2 1 0 0 1 2 3 4 5 Pixel Column Number

Line Drawing Algorithms • Cartesian slope-intercept equation for straight line y = mx + b Slope m = y 2 –y 1 x 2 –x 1 X의 Interval Δx Y의 Interval Δy에 대해 Δy = m Δx Δy Δx = m -----(1) -----(2) y 2 y 1 x 2

Line Drawing Algorithms • DDA(Digital Differential Analyzer) - left endpoint → right endpoint if slope m <= 1 then unit x interval Δx (Δx = 1) Yk+1 = Yk + m ----------(3) if slope m >= 1 then unit y interval Δy (Δy = 1) Xk+1 = Xk + 1 ----------(4) m - right endpoint → left endpoint Δx = -1, Δy = -1

Line Drawing Algorithms # include “device. h” #define ROUND(a) ((int) (a+0. 5)) void line. DDA (int xa, int ya, int xb, int yb) { int dx = xb – xa, dy = yb – ya, steps, k; float x. Increment, yincrement, x = xa, y = ya; if (abs(dx) > abs(dy)) steps = abs(dx); else steps = abs(dy); x. Increment = dx/(float) steps; y. Increment = dy/(float) steps; set. Pixel (ROUND(x), ROUND(y)); for (k=0; k < steps ; k++) { x += x. Increment; y += y. Increment; set. Pixel (ROUND(x), ROUND(y)); } }

Line Drawing Algorithms • DDA Algorithm의 장단점 - 장점 : Cartesian slope equation보다 빠르다. - 단점 Roundoff error의 누적으로 실제 line path에서 drift되어 pixel position이 계산된다. Cartesian slope equation보다 빠르지만, Rounding, floating point 계산은 time-consuming

Line Drawing Algorithms • Bresenham’s Line Algorithm - only incremental integer calculation을 사용 14 13 12 11 10 Specified Line Path 10 11 12 13 14 15 - Specified Line Path가 지나치는 두개의 선택가능한 pixel중에서 어느쪽이 Line Path에 더 가까운가로 pixel position 결정

Line Drawing Algorithms • Bresenham’s Line Drawing Algorithm for |m| < 1 일때 Yk+3 Yk+2 Yk+1 Yk y = mx + b Xk Xk+1 Xk+2 Yk+1 y Yk d 2 d 1 Xk+1 y = m(Xk+1) + b d 1 = y - Yk = m(Xk + 1) + b –Yk d 2 = (Yk + 1) – y = (Yk + 1) – m(Xk + 1) – b If d 1 – d 2 > 0 then Yk + 1 else Yk

Line Drawing Algorithms • Decision Parameter Pk = Δx(d 1 – d 2) = 2 Δy* Xk - 2 Δx* Yk + c ----(5) Pk+1 = 2 Δy* Xk+1 - 2 Δx* Yk+1 + c Pk+1 - Pk = 2 Δy(Xk+1 – Xk) - 2 Δx(Yk+1 - Yk) unit step을 x direction으로 하므로 Xk+1 = Xk + 1 Pk+1 = Pk + 2 Δy - 2 Δx(Yk+1 - Yk) Yk+1 – Yk 는 0, 1 이므로, (5)식을 이용하여 first decision parameter P 0 = 2 Δy – Δx starting pixel position (X 0, Y 0), m = Δy /Δx

Line Drawing Algorithms • Bresenham’s Line Drawing Algorithm for |m| < 1 1. Input the two line endpoint and store the left endpoint in (X 0, Y 0 ). 2. Load (X 0, Y 0 ) into the frame buffer, that is, plot the first point. 3. Calculate constants Δx, Δy, and 2Δy - 2 Δx, and obtain the starting value for decision parameter as P 0 = 2 Δy – Δx 4. At each Xk along the line, starting at k= 0, perform the following test: If Pk < 0, the next point to plot is (Xk + 1, Yk) and Pk+1 = Pk + 2 Δy otherwise, the next point to plot is (Xk + 1, Yk + 1) and Pk+1 = Pk + 2 Δy - 2 Δx 5. Repeat step 4 Δx times.
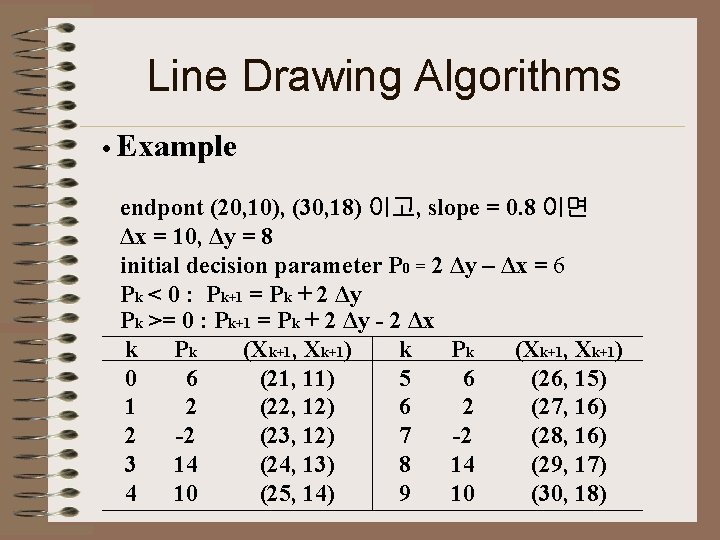
Line Drawing Algorithms • Example endpont (20, 10), (30, 18) 이고, slope = 0. 8 이면 Δx = 10, Δy = 8 initial decision parameter P 0 = 2 Δy – Δx = 6 Pk < 0 : Pk+1 = Pk + 2 Δy Pk >= 0 : Pk+1 = Pk + 2 Δy - 2 Δx k Pk (Xk+1, Xk+1) 0 6 (21, 11) 5 6 (26, 15) 1 2 (22, 12) 6 2 (27, 16) 2 -2 (23, 12) 7 -2 (28, 16) 3 14 (24, 13) 8 14 (29, 17) 4 10 (25, 14) 9 10 (30, 18)
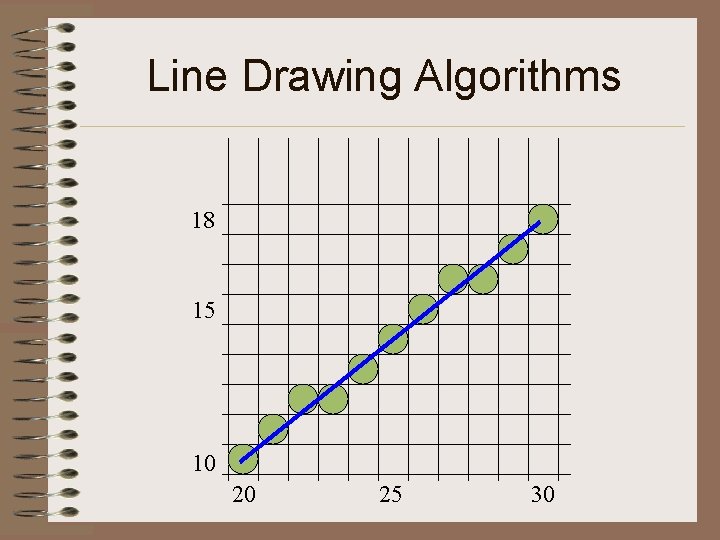
Line Drawing Algorithms 18 15 10 20 25 30
Line Drawing Algorithms • |m| > 1 일때, x, y의 역할 변경 즉, |m| < 1일때, unit step을 x direction으로 하여 Xk+1 = Xk + 1, 그에 따른 y값의 변화를 적용한것 처럼 unit step을 y direction으로 하고, 그에 따른 x의 값의 변화를 적용 • right endpoint → left endpoint 일때는 x, y value decrease • Horizontal Line(Δy = 0) Vertical Line(Δx = 0) diagonal Line(|Δx| = |Δy|) Frame buffer에서 직접 load
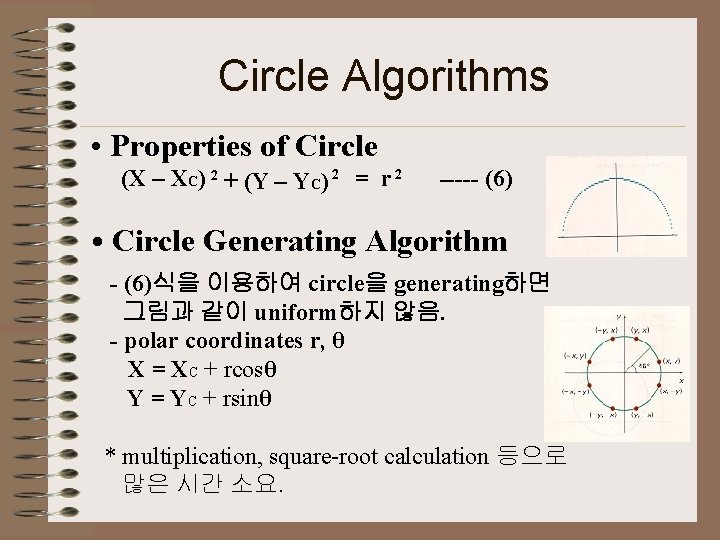
Circle Algorithms • Properties of Circle (X – XC) 2 + (Y – YC) 2 = r 2 ----- (6) • Circle Generating Algorithm - (6)식을 이용하여 circle을 generating하면 그림과 같이 uniform하지 않음. - polar coordinates r, θ X = XC + rcosθ Y = YC + rsinθ * multiplication, square-root calculation 등으로 많은 시간 소요.
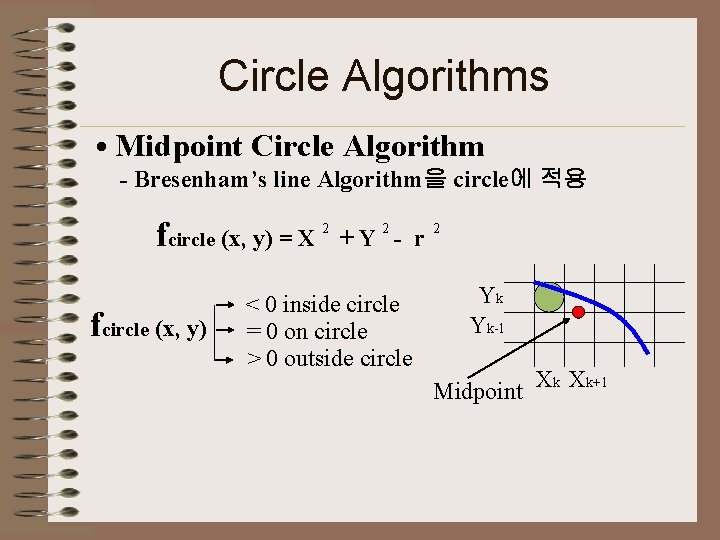
Circle Algorithms • Midpoint Circle Algorithm - Bresenham’s line Algorithm을 circle에 적용 fcircle (x, y) = X fcircle (x, y) 2 2 +Y - r < 0 inside circle = 0 on circle > 0 outside circle 2 Yk Yk-1 Midpoint Xk Xk+1

Circle Algorithms • Midpoint Circle Algorithm 1. Input radius r and circle center (XC, YC), and obtain the first point on the circumference of a circle center on the origin as (X 0, Y 0) = (0, r) 2. Calculate the initial value of the Decision parameter as P 0 = 5 - r → P 0 = 1 – r (for r an integer) 4 3. At each Xk, starting k = 0 : If Pk < 0, next point (Xk+1, Yk) and Pk+1 = Pk +2 Xk+1 + 1 else, next point (Xk+1, Yk-1) and Pk+1 = Pk +2 Xk+1 + 1 - 2 Yk+1 where 2 Xk+1 = 2 Xk + 2, 2 Yk+1 = 2 Yk - 2, 4. Determine symmetry points in the other seven octants. 5. Move acutual circle center (x, y) 6. Repeat step 3 through 5 until x >= y.

Circle Algorithms • Example r = 10, (Xc, Yc) = (0, 0) 일때 P 0 = 1 – r = 9 (X 0, Y 0) = (0, 10) 이므로 2 X 0 = 0, 2 Y 0 = 20 k Pk (Xk+1, Xk+1) 2 Xk+1 2 Yk+1 0 -9 (1, 10) 2 20 1 -6 (2, 10) 4 20 2 -1 (3, 10) 6 20 3 6 (4, 9) 8 18 4 -3 (5, 9) 10 18 5 8 (6, 8) 12 16 6 5 (7, 7) 14 14
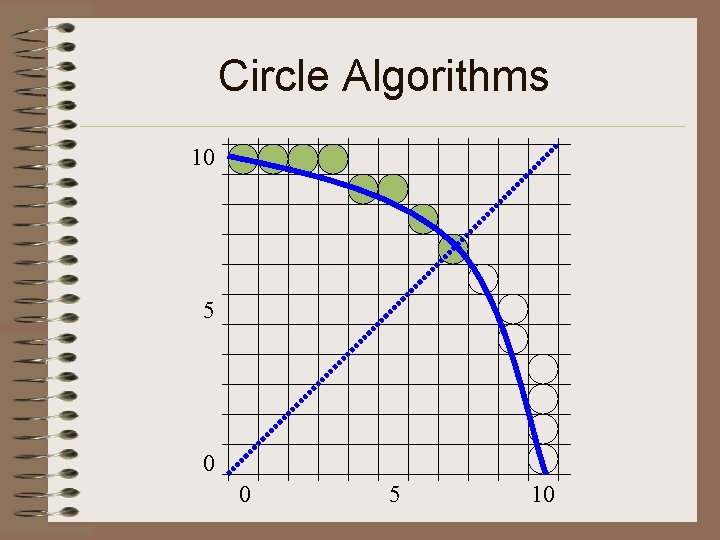
Circle Algorithms 10 5 0 0 5 10

Filled-Area Primitives • Area filling on raster system - scan-line fill algorithm : polygon, circle, ellipses, simple curves - boundary fill algorithm : more complex boundaries, interactive system - flood fill algorithm • Inside – Outside Test - odd-even rule - nonzero winding number rule

Scan-Line Fill Algorithm • Check the intersection points of the scan line with the polygon edges • Vertices handling • Store the sorted edge table - maximum y value for that edge - x-intercept value at lower vertex for the edge - the inverse slop of the edge • Produce the active edge list

Scan-Line Fill Algorithm • Check the intersection points y x • Vertices handling : scan line passing through a vertex intersects two edges. : trace around polygon boundary → clockwise or counterclockwise : observe relative change in vertex y coordinates as we move one edge to the next.
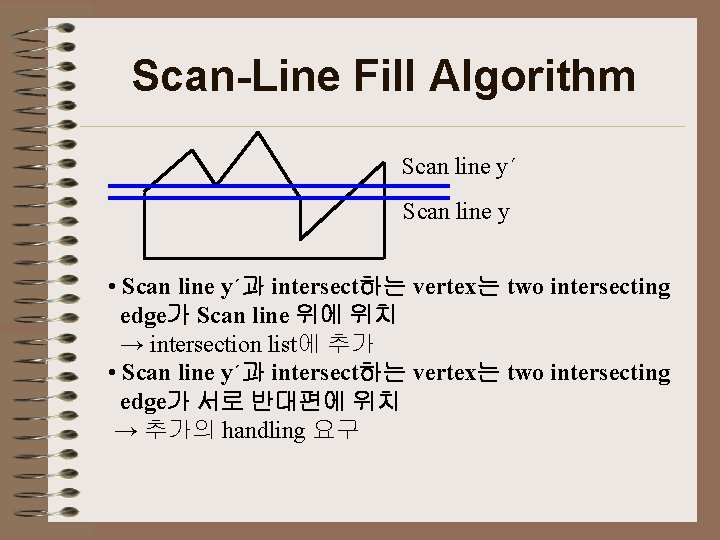
Scan-Line Fill Algorithm Scan line y´ Scan line y • Scan line y´과 intersect하는 vertex는 two intersecting edge가 Scan line 위에 위치 → intersection list에 추가 • Scan line y´과 intersect하는 vertex는 two intersecting edge가 서로 반대편에 위치 → 추가의 handling 요구

Scan-Line Fill Algorithm • handling 방법 : shortening lower edge to split vertices. - y value increasing : 현재 edge의 upper endpoint 1 감소 - y value decreasing : 다음 edge의 upper endpoint 1 감소 Scan line y+1 Scan line y-1
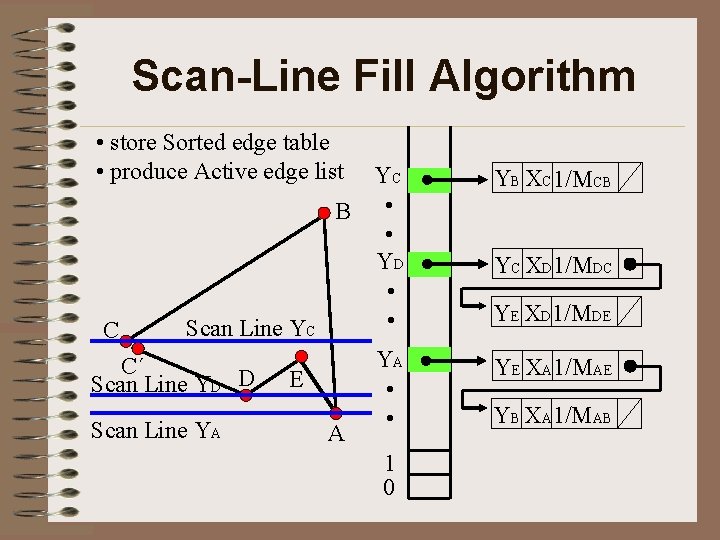
Scan-Line Fill Algorithm • store Sorted edge table • produce Active edge list C Scan Line YC C´ Scan Line YD D Scan Line YA YC B • • YD • • E A YA • • 1 0 YB XC 1/MCB YC XD 1/MDC YE XD 1/MDE YE XA 1/MAE YB XA 1/MAB

Boundary Fill Algorithm • Point inside a region → Boundary • Input interior point(x, y) • Test neighboring positions until all pixels up to boundary color - boundary color then stop - otherwise, fill color • 4 -connected boundary fill algorithm • 8 -connected boundary fill algorithm • Horizontal pixel spans across scan lines
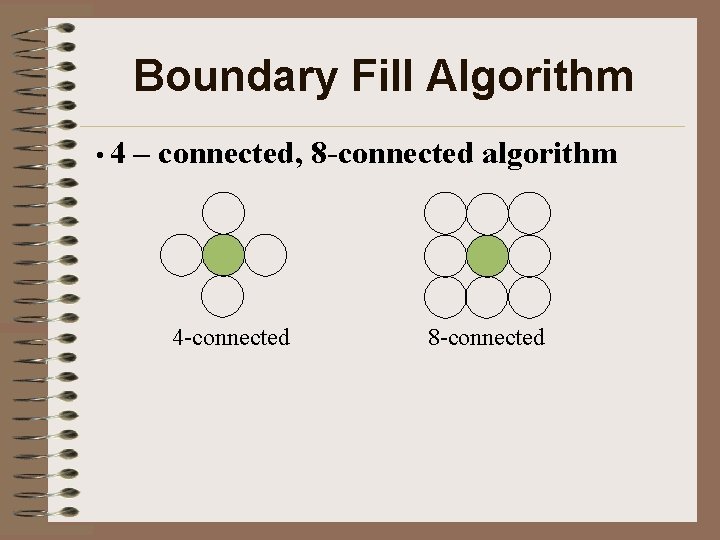
Boundary Fill Algorithm • 4 – connected, 8 -connected algorithm 4 -connected 8 -connected
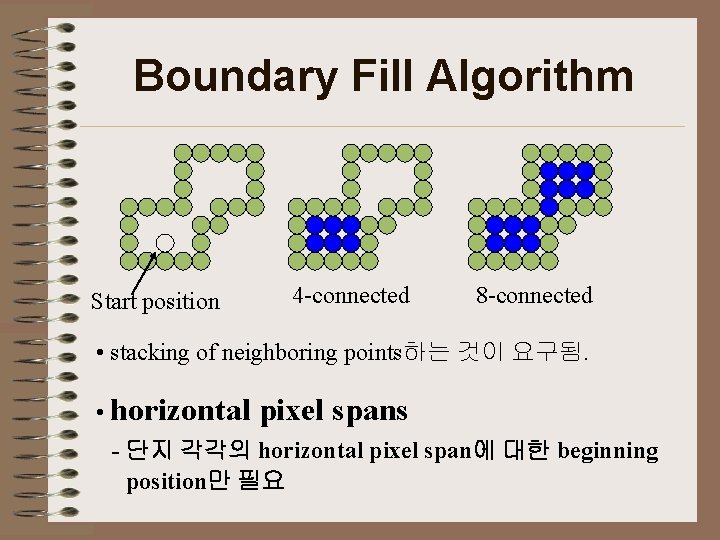
Boundary Fill Algorithm Start position 4 -connected 8 -connected • stacking of neighboring points하는 것이 요구됨. • horizontal pixel spans - 단지 각각의 horizontal pixel span에 대한 beginning position만 필요
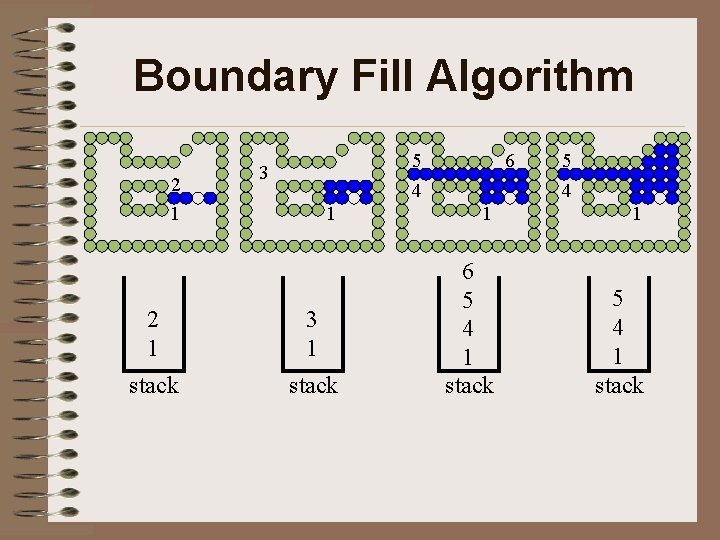
Boundary Fill Algorithm 2 1 5 4 3 6 5 4 1 1 1 2 1 3 1 stack 6 5 4 1 stack

Boundary Fill Algorithm • Flood-Fill Algorithm • Single color boundary가 아닌 경우의 interior fill method - start from a interior point - reassign all pixel values : given interior color → desired fill color - more than one interior color일때 → all interior color를 same color로 reassign - 4 – connected, 8 – connected 기법 이용

Inside-Outside Test • Odd – even rule - polygon 내의 임의의 점 P → polygon 좌표축에서 상당히 벗어난 거리의 점과의 line을 drawing. - 이 line과 polygon edge의 교차되는 number counting. - odd number : 점 P는 interior point - even number : 점 P는 exterior point
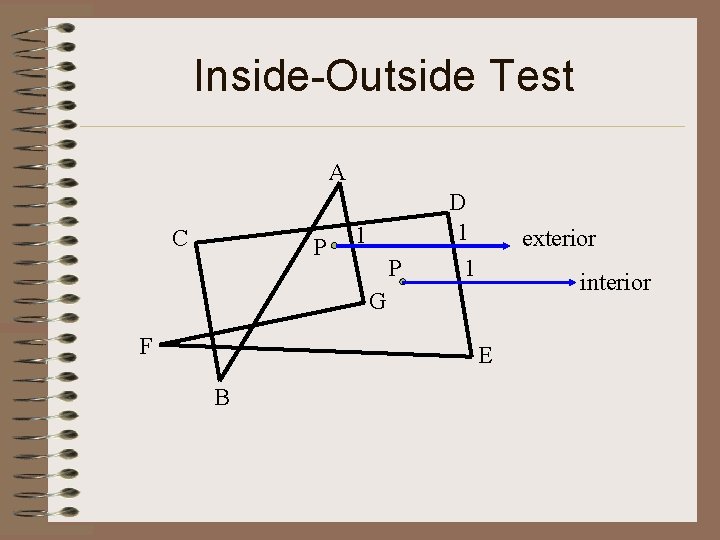
Inside-Outside Test A C P 1 P D 1 1 exterior interior G F E B

Inside-Outside Test • Nonzero winding number rule - polygon edges에 counter-clockwise방향으로 도는 vector 생성 - ploygon 내의 점 P → polygon 좌표축에서 상당히 벗어난 거리의 점 방향으로의 vector line을 drawing. - 두 vector의 intersect 방향 check initial winding number = 0 : right → left 이면 winding number + 1 : left → right 이면 winding number – 1 - Winding number가 nonzero이면 interior point Winding number가 nonzero 아니면 exterior point

Inside-Outside Test
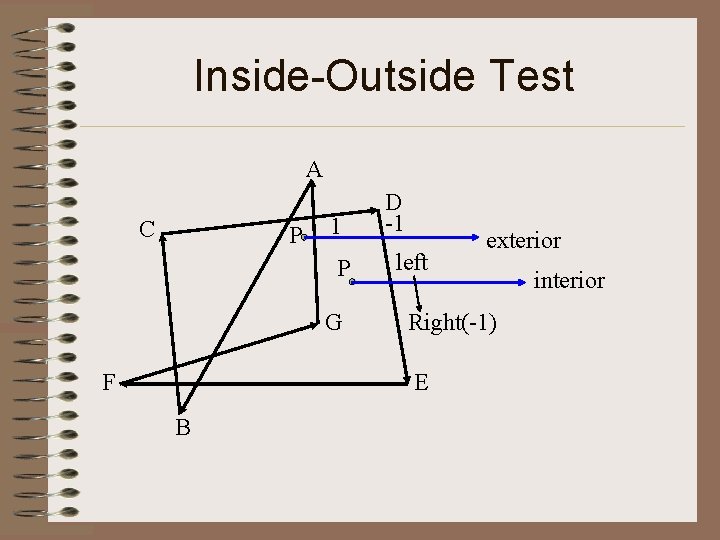
Inside-Outside Test A C P 1 P G F D -1 left Right(-1) E B exterior interior
- Slides: 37