Scaling functions Fix filter or connect the dots




















- Slides: 21

Scaling functions Fix filter ‘or connect the dots’ no restrictions yet: FUND. DEFN: Scaling Function relates at two levels of resolution. Basic condition:

Examples so far: Box: Tent centered at : Daubechies D 4: does there exist ?

Fractal example:

Dyadic rationals: determined at dyadic rationals : Convolution on integers? Powers of 2? KNOW Construct ALL , THEN KNOW on all ALL as limiting fixed point!

Iterative process: with limit Construct sequence functions such that Then What about convergence? Pointwise, in Energy? Pointwise: start with Tent function In energy: start with Box function

Getting started: Tent function centered at origin: Basic idea: set for suitable

Filter conditions: Need so that Conditions on : Solve using Fourier Transforms as usual. in

Fourier Transforms: Set Then So:

Up-sampling again! Recall Crucial results: where in z-transform notation: Use these to compute .

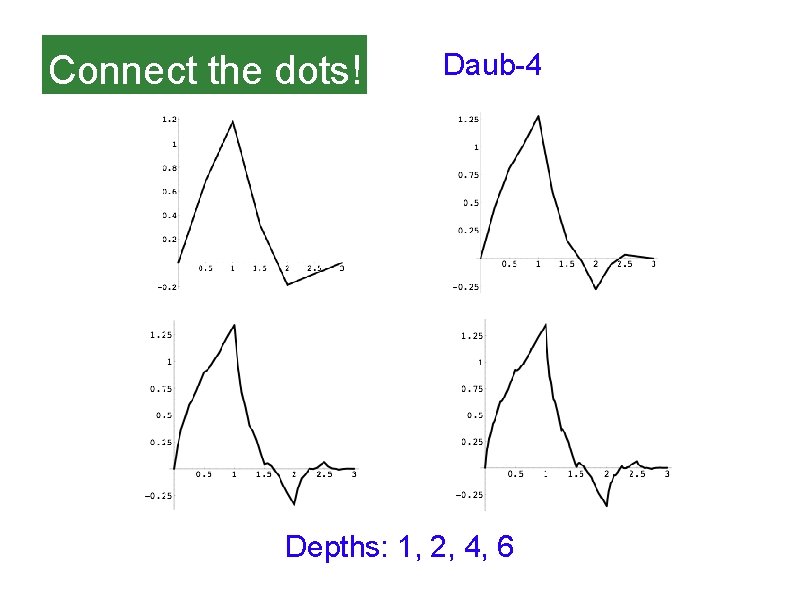
Connect the dots! Daub-4 Depths: 1, 2, 4, 6

Cascade Algorithm: convergence in energy Start with box function: can exploit orthonormality. with as before, but no Vetterli condition yet. So

Orthonormality: Case: k = 0 Can we recognize sequence: ?

Finally Vetterli! Consider first: Crucial identification: Fourier transform:

Finally Vetterli! When we deduce that So , hence , ORTHONORMAL FAMILY for each k.

In the limit! When in energy, then so Vetterli ensures orthonormal family in .

Finally wavelets: Fix FIR filter Assume convergence in energy and Vetterli. Set define wavelet by compactly supported if By same argument as for d to identify compactly supported. : .

More results for wavelets: Recall , so By Vetterli yet again: so Thus , orthonormal family.

Still more results: By same argument yet again: But by Fourier transforms yet again: where remember, . Thus: all.

Main Theorem Part 1: FIR filter If then is a continuous function with derivatives.

Main Theorem Part 2: Suppose also satisfies Vetterli condition. Define wavelet: . Then: 1. orthonormal families, , , 2. 3. complete orthonormal family in .

Main Theorem applied to Daub-4: so hence Daub-4 continuous, not quite differentiable
 Lesson 31 connect the dots lewis
Lesson 31 connect the dots lewis Connect all dots without crossing the lines
Connect all dots without crossing the lines What is the maximum number of pieces
What is the maximum number of pieces Perbedaan rapid sand filter dan slow sand filter
Perbedaan rapid sand filter dan slow sand filter Iir filter design by approximation of derivatives
Iir filter design by approximation of derivatives Difference between rapid sand filter and slow sand filter
Difference between rapid sand filter and slow sand filter Shifting and scaling functions
Shifting and scaling functions Shifting and scaling functions
Shifting and scaling functions Farnsworth morse
Farnsworth morse Count the dot audiogram
Count the dot audiogram Dot
Dot Which artist utilized benday dots in his artwork
Which artist utilized benday dots in his artwork Dot wall
Dot wall Peripheral smear of plasmodium falciparum
Peripheral smear of plasmodium falciparum Dot and screed plastering
Dot and screed plastering Trantas dots
Trantas dots Pharmacy dots initiative
Pharmacy dots initiative Think dots differentiated instruction
Think dots differentiated instruction Think dots differentiated instruction
Think dots differentiated instruction K3p lewis structure
K3p lewis structure Darko odic
Darko odic History of quantum dots
History of quantum dots