Scale Factor Scale Drawings Understanding Scales All scale

Scale Factor & Scale Drawings

Understanding Scales All scale drawings must have a scale written on them. Scales are usually expressed as ratios. Normally for maps and buildings the ratio: Drawing length: Actual length For maps the ratio is normally in the ratio: Map distance: Actual Distance Example: 1 cm : 100 cm The ratio 1 cm: 100 cm means that for every 1 cm on the scale drawing the length will be 100 cm in real life Example: 1: 10000 The ratio 1: 10000 means that the real distance is 10000 times the length of one unit on the map or drawing.

Scale Factor

How to find Scale Factor When a figure is dilated, its size is changed by multiplying the length of each side by a scale factor. All angles remain the same and so the new shape (or image) is similar to the original. Can be found by dividing a new side length by the original side length. • When going from a small shape to a larger shape the scale factor is greater than 1. (Enlargement) • When going from a large shape to a smaller shape the scale factor is • less than 1. (Reduction) 1. 2. 3. 4. Determine the corresponding side lengths. Determine if you are making a larger shape or a smaller shape. Determine if the scale factor is greater than or less than 1. Write the correct ratio.

Scale Factor Scale factor = new measurement old measurement Old measurement x SF = new measurement new SF old - Scale factor more than 1 => shape gets bigger (Enlargement) - Scale factor less than 1 => shape gets smaller (Reduction) - Congruent shapes are similar shapes with SF = 1

Vocabulary scale model scale factor scale drawing

The scale can be written as a scale factor, which is the ratio of the length or size of the drawing or model to the length of the corresponding side or part on the actual object. Scale Factor needs to be the SAME UNITS!

This HO gauge model train is a scale model of a historic train. A scale model is a proportional model of a three-dimensional object. Its dimensions are related to the dimensions of the actual object by a ratio called the scale factor. The scale factor of an HO 1 gauge model train is . 87 1 This means that each dimension of the model is 87 of the corresponding dimension of the actual train.

A scale is the ratio between two sets of measurements. Scales can use the same units or different units. The photograph shows a scale drawing of the model train. A scale drawing is a proportional drawing of an object. Both scale drawings and scale models can be smaller or larger than the objects they represent.

If you have ever seen Jurassic Park, you saw how big the dinosaurs were compared to the people. Pretend that they made a large Human to watch over the animals. What would be the scale factor if a 64 inch person was made to be 160 feet?

The scale factor tells you how many times bigger than “normal” that person really is. You must make all units of measure the same…. 64 inches = = 160 feet 160 x 12 1920 inches

Now take the: 64 inches 1920 inches And simplify 1/30 inches This means that the person was created 30 times his normal size.

Scale Factor

Setting up Proportions Keep like units in the same fraction. Inches = yards Inches yards

Remember… There is more than one way to set up a proportion correctly! Cross Multiply! Use common sense!

Write a Proportion Using Scale Factor Tom is drawing a blueprint for a rectangular shed he wants to build. The scale factor is 1 ft. to ¼ inch. If the dimensions of the blueprint are 1 ¼ in. by 2 inches, what are the actual dimensions of the shed going to be?

Write a Proportion Using a Scale Factor ¾ inch to 1 foot If the length in inches is 2 ¼ inch, what would the actual length be in feet ?

Scale Drawings

What are scale drawings? Scale drawings are everywhere! Scale Drawings On Maps Vehicle design Footprints of houses

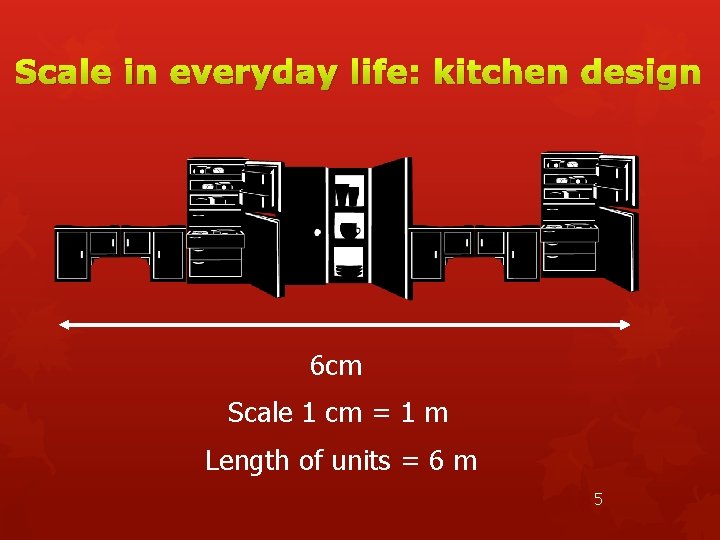
Scale in everyday life: kitchen design 6 cm Scale 1 cm = 1 m Length of units = 6 m 5

Scale in everyday life: maps Scale 1 : 1 000

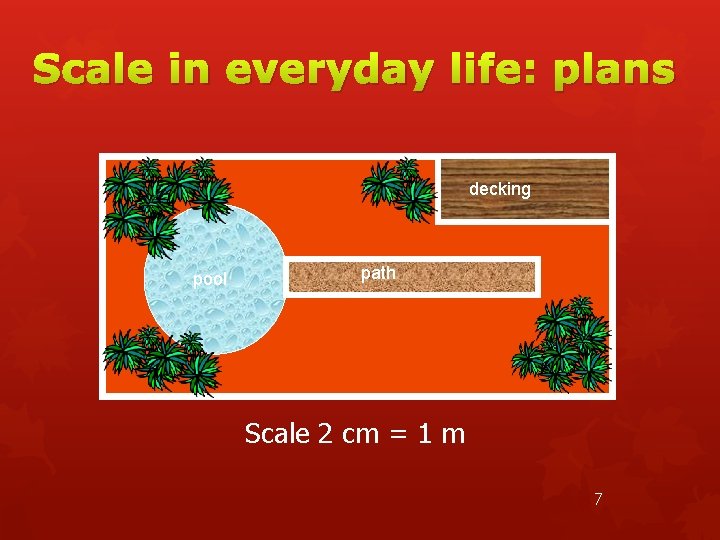
Scale in everyday life: plans decking pool path Scale 2 cm = 1 m 7

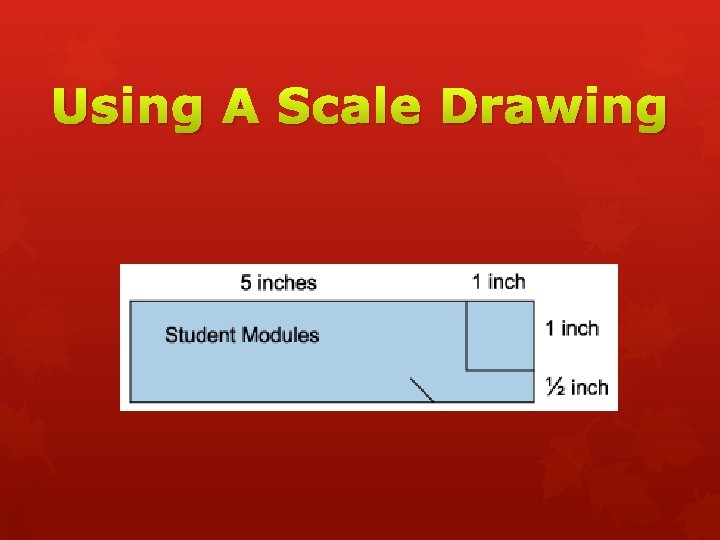
Using A Scale Drawing

When objects are too small or too large to be drawn or constructed at actual size, people use a scale drawing or a model. The scale drawing of this tree is 1: 500 If the height of the tree on paper is 20 inches, what is the height of the tree in real life?

The scale is the relationship between the measurements of the drawing or model to the measurements of the object. In real-life, the length of this van may measure 240 inches. However, the length of a copy or print paper that you could use to draw this van is a little bit less than 12 inches

Map Scales (Legends) are used to find distances on a map. For example, if your map legend tells you that ½ of an inch represents 50 miles, how could you find the mileage for a 2 inch distance on the map?

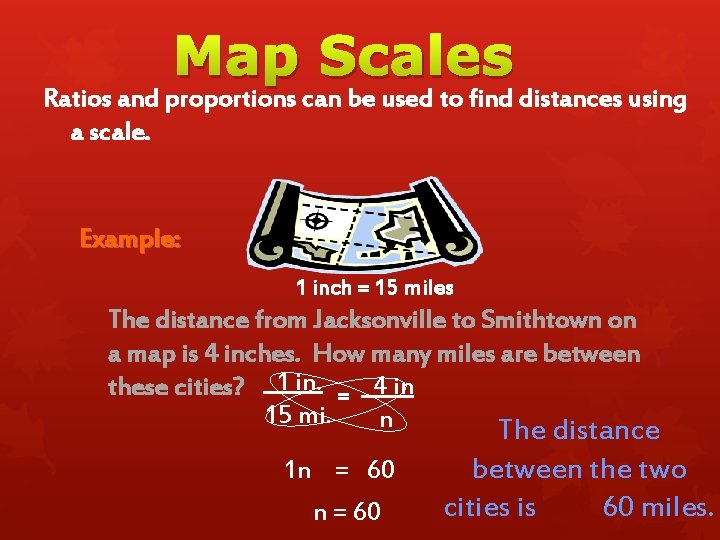
Map Scales Ratios and proportions can be used to find distances using a scale. Example: 1 inch = 15 miles The distance from Jacksonville to Smithtown on a map is 4 inches. How many miles are between these cities? 1 in. = 4 in 15 mi. n The distance 1 n = 60 between the two cities is 60 miles.