Scale Factor and the relationship to area and

Remember these rules !! If 2 number shapesthat arewe The similar, byit is the

Let’s review, what we know about similar shapes. 1. 75 cm 2. 8 =

Remember: if shapes are similar it is because they are related by multiplication. If

1. 75 cm 2. 8 cm 3. 5 cm 5. 6 cm The second

1. 75 cm The rule: to find the area of the 2. 8 cm

Since the Remember, you 1. 75 cm scale factor is 2, the are shape

The second tripled in size, so the scale factor is 3 The area of

The reason this works is because area is increased by length and width. If

2 m 6 m 18 m 2 = 3 The second shape is 3

10 cm If the scale factor is ½ what would be the area of

Now let’s look at scale factor and volume. The rule is to multiply the

5 cm 10 cm 30 cm The scale factor is 3, because the size

5 m 30 m 5 m 10 m What is the scale factor? ½

Now Check yourself !! length width Scale factor 2 15 10 Answers: 600 3

Now Check yourself !! : s r e 3 6 w s height Scale

Slides: 19

Download presentation

Scale Factor and the relationship to area and volume GLE 0706. 2. 3 0706. 4. 3 SPI: 0706. 2. 7 0706. 4. 3

Remember these rules !! If 2 number shapesthat arewe The similar, byit is the by multiplication scale factor. Scale factor is the ratio of corresponding parts.

Let’s review, what we know about similar shapes. 1. 75 cm 2. 8 = 1. 75 5. 6 x m c 5 . 3 x= x 5. 6 cm 9. 8 = 2. 8 x 2. 8

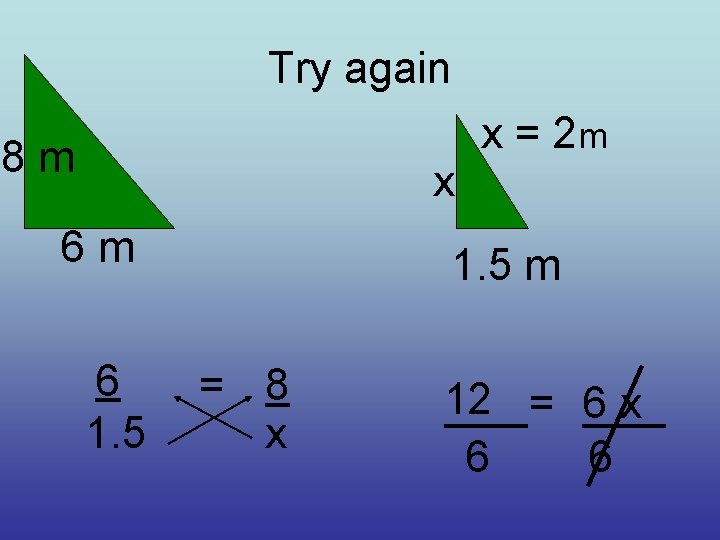
Try again 8 m x 6 m 6 1. 5 x = 2 m 1. 5 m = 8 x 12 = 6 x 6 6

Remember: if shapes are similar it is because they are related by multiplication. If a shape doubles, the scale factor is 2; if the shape triples in size, the scale factor is 3, and so on.

1. 75 cm 2. 8 cm 3. 5 cm 5. 6 cm The second quadrilateral is twice as tall and twice as wide. This means the scale factor is 2.

Scale factor and Area

1. 75 cm The rule: to find the area of the 2. 8 cm second shape The scale factor is 2, so multiply the area its is times 4… ofsquare the first let’s it. factor thetest scale 3. 5 cm squared. 5. 6 cm

Since the Remember, you 1. 75 cm scale factor is 2, the are shape is twice as 2. 8 cm (using l * w) scale factor 2 the scale tall and twice as wide. 2 1. 75 to x find 2. 8 area x 2 factor when don’t 1. 75 you x 2. 8 x 4= 3. 5 cm know the length of 2 19. 6 cm Check yourself. . all the sides. is that = to 5. 6 cm 5. 6 x 3. 5 ?

The second tripled in size, so the scale factor is 3 The area of the second: 2 Area of first x 6 4 5 15 10 x 32 10 x 9 = 90 Yes, 15 if*you 12 use = 90 Is this½true the formula ½ b x h

The reason this works is because area is increased by length and width. If both dimensions are increased, you are square – ing.

2 m 6 m 18 m 2 = 3 The second shape is 3 x as big, so the scale factor is 3. The area of the first times the Scale factor 2. 12 x = 2 12 x 9 108 m

10 cm If the scale factor is ½ what would be the area of the smaller? Area of the first times 2 the scale factor 10 * (1/2)2= 100 * ¼ = 25 cm 2

Scale factor and volume

Now let’s look at scale factor and volume. The rule is to multiply the volume of the known times the scale factor 3. Remember you are increasing the length, width, and height of a shape, thus cube - ing.

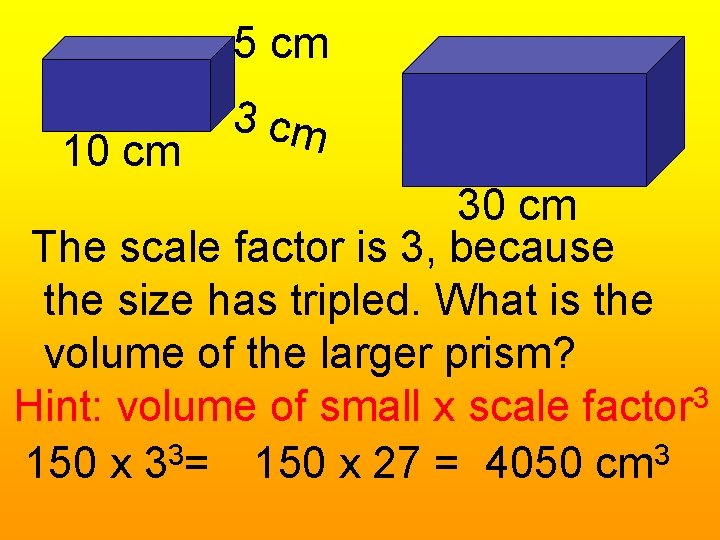
5 cm 10 cm 30 cm The scale factor is 3, because the size has tripled. What is the volume of the larger prism? 3 Hint: volume of small x scale factor 150 x 33= 150 x 27 = 4050 cm 3

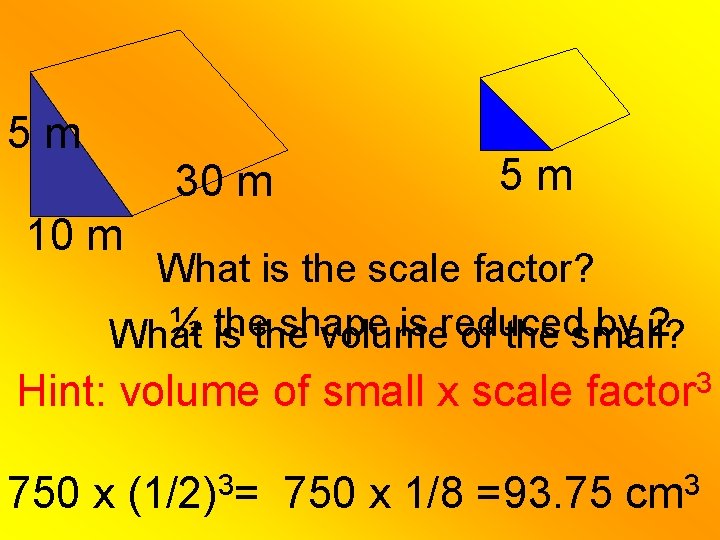
5 m 30 m 5 m 10 m What is the scale factor? ½ is thethe shape is reduced by 2 What volume of the small? Hint: volume of small x scale factor 3 750 x 3 (1/2) = 750 x 1/8 =93. 75 3 cm

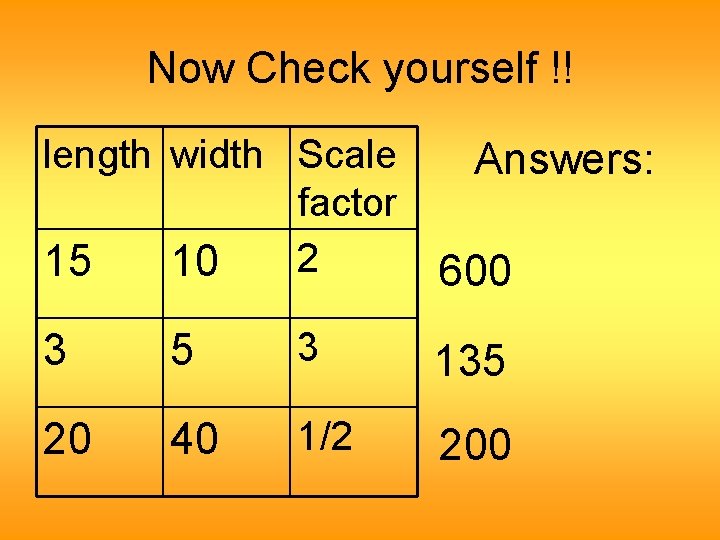
Now Check yourself !! length width Scale factor 2 15 10 Answers: 600 3 5 3 135 20 40 1/2 200

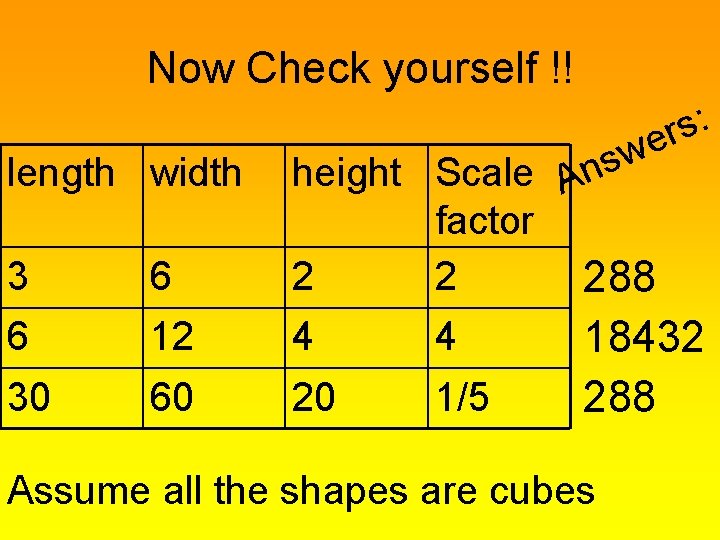
Now Check yourself !! : s r e 3 6 w s height Scale An factor 2 2 288 6 12 4 4 30 60 20 1/5 length width 18432 288 Assume all the shapes are cubes