Scale Drawings and Scale Models We will apply

Scale Drawings and Scale Models We will apply proportional relationships to scale drawings and models.

A scale drawing is a drawing that is similar, but either larger or smaller than the actual object.

A scale model is used to represent something that is too large or too small for an actual size model.

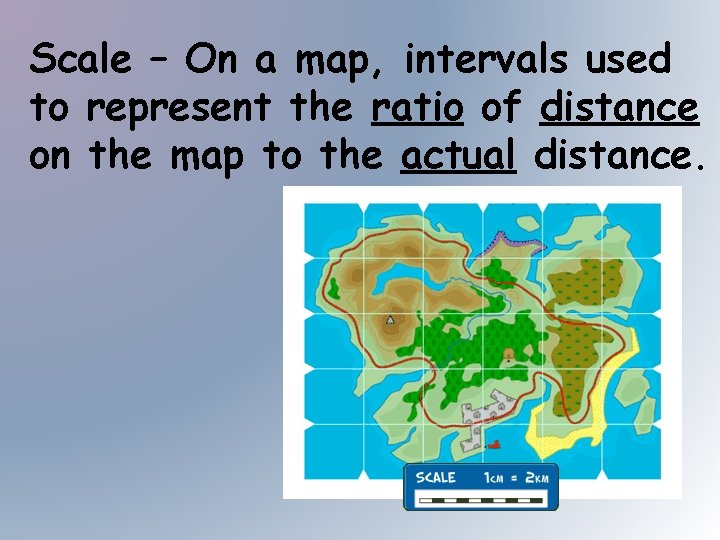
Scale – On a map, intervals used to represent the ratio of distance on the map to the actual distance.

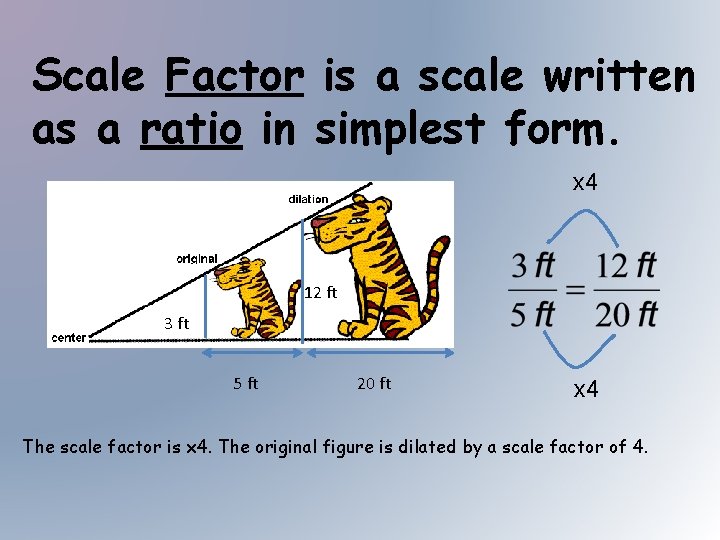
Scale Factor is a scale written as a ratio in simplest form. x 4 12 ft 3 ft 5 ft 20 ft x 4 The scale factor is x 4. The original figure is dilated by a scale factor of 4.

A map is an example of a scale drawing. Scale drawings and scale models are used to represent objects that are too large or too small to be drawn or built to actual size. The scale gives the ratio that compares the scale drawing or model to the real object. The measurements are proportional.

Example 1: A model of a tree is made using the scale of 1 inch = 10 feet. What is the height of the actual tree if the height of the model is 4 inches? Model Actual 1 inch 4 inches 10 feet ? feet 40 = 1 x 1 1 40 = x

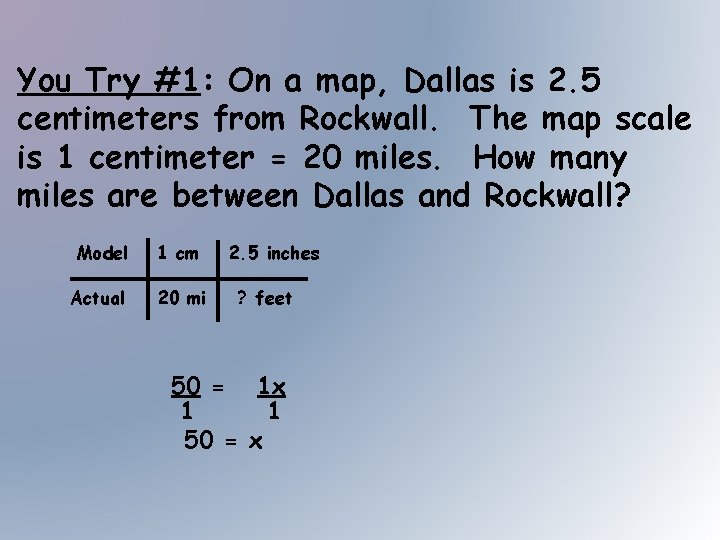
You Try #1: On a map, Dallas is 2. 5 centimeters from Rockwall. The map scale is 1 centimeter = 20 miles. How many miles are between Dallas and Rockwall? Model 1 cm Actual 20 mi 2. 5 inches ? feet 50 = 1 x 1 1 50 = x

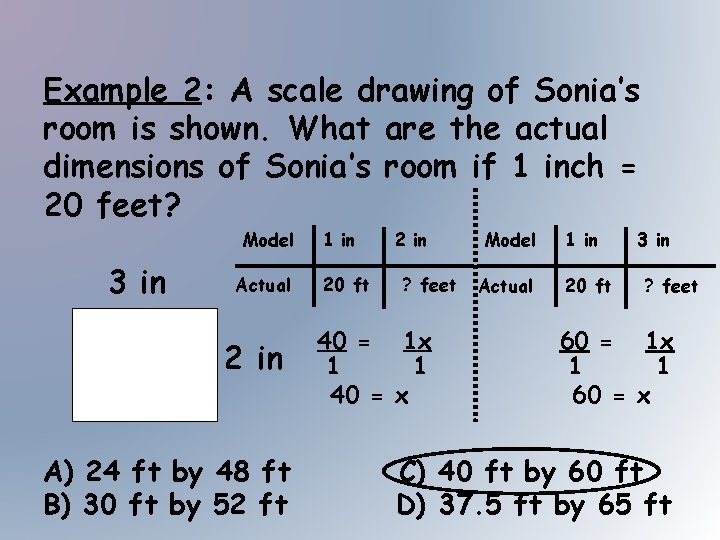
Example 2: A scale drawing of Sonia’s room is shown. What are the actual dimensions of Sonia’s room if 1 inch = 20 feet? Model 3 in Actual 2 in A) 24 ft by 48 ft B) 30 ft by 52 ft 1 in 20 ft 2 in ? feet 40 = 1 x 1 1 40 = x Model Actual 1 in 20 ft 3 in ? feet 60 = 1 x 1 1 60 = x C) 40 ft by 60 ft D) 37. 5 ft by 65 ft

Example 3: The model of the building is 24 inches tall. The actual building is 96 feet tall. What scale is being used? Model 24 in Actual 96 ft 1 in ? feet 96 = 24 x 24 24 4 = x

You Try #2: Ernie drew a map of his school. He used a scale in which 1 inch equals 50 feet. What distance on Ernie’s map should represent the 625 feet between the cafeteria and the science lab? A) 8 in B) 10. 5 in C) 12. 5 in D) 15 in