SAYISAL VERLERN SINIFLANDIRILMASI Snf etele Frekans 10 19












- Slides: 18

SAYISAL VERİLERİN SINIFLANDIRILMASI Sınıf Çetele Frekans % 10 -19 //// 4 5 20 -29 ////// 6 12

Sayısal Verilerin Sınıflandırılması Sayısal veriler için elde edilecek en kolay sınıflandırma, basit frekans dağılımlarının elde edilmesidir. Bunun için: veriler küçükten büyüğe (ya da büyükten küçüğe) doğru sıralanarak her bir gözlemden kaçar tane olduğu gözlemlerin karşısına yazılır.

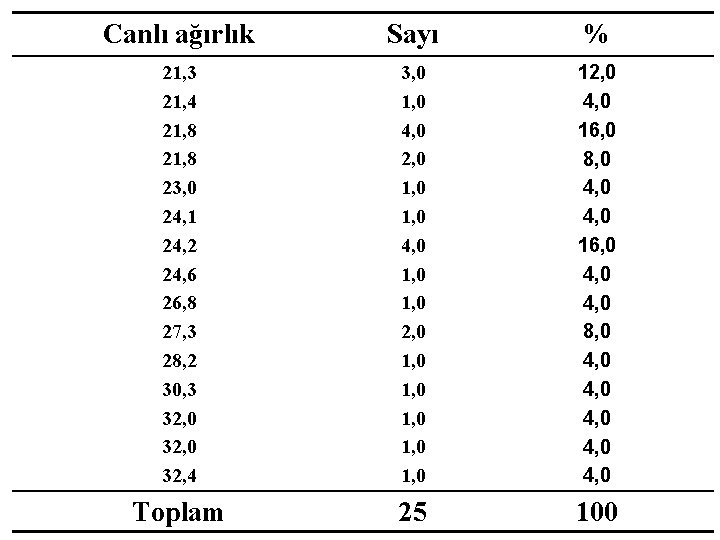
Canlı ağırlık Sayı % 21, 3 21, 4 21, 8 23, 0 24, 1 24, 2 24, 6 26, 8 27, 3 28, 2 30, 3 32, 0 32, 4 3, 0 1, 0 4, 0 2, 0 1, 0 4, 0 1, 0 2, 0 1, 0 12, 0 4, 0 16, 0 8, 0 4, 0 16, 0 4, 0 8, 0 4, 0 4, 0 Toplam 25 100

Ancak dağılım aralığı (en büyük değerle en küçük değer arasındaki fark) büyüdükçe basit frekans dağılımları kullanışsızlaşır. Bu durum gözlem sayısının arttığı durumlarda daha da belirginleşir. Bu nedenle veriler sınıflandırılır.

Sınıflandırma işlemlerinin belli adımları vardır. Sınıflandırmada kullanılan tanımlar: 1. Sınıf Sayısı: Oluşturulacak sınıf sayısıdır. Örnek: 50 -54 55 -59 60 -64 65 -69 70 -74 Burada sınıf sayısı 5’tir

2. Sınıf Sınırı: Oluşturulacak her sınıfın bir alt ve bir üst sınırı vardır. Bu sınırlara sınıf sınırları denir. Örneğin 50 -54 sınıfının alt sınırı 50 üst sınırı 54’tür. 3. Sınıf Aralığı (c): Ard arda gelen iki sınıfın üst sınırları ya da alt sınırları arasındaki farka sınıf aralığı denir. Yukarıdaki örnek için sınıf değeri= 2. Sınıfın alt sınır değeri ile 1. Sınıfın alt sınır değeri arasındaki fark 55 -50=5’tir.

4. Sınıf Değeri: Her sınıfın alt ve üst sınır değerlerinin toplamının yarısıdır. Örneğin herhangi bir sınıfın alt sınırı 50 üst sınırı 54 ise Sınıf Değeri=(50+54)/2=52 5. Dağılım Aralığı: Dağılımdaki en büyük değerden en küçük değerin çıkartılması ile bulunur.

Sınıflandırma İşleminde Dikkat Edilecek Noktalar Sınıflandırma sonucunda, dağılımdaki bütün değerler sınıflara dağıtılabilmeli ve hiçbir değer sınıflama dışında kalmamalıdır. Örneğin canlı ağırlık verileri 20 -25 26 -30 31 -35 biçiminde olsaydı sınıflandırma işlemi yanlış olurdu. Çünkü 25 -26 ve 30 -31 arasında değerler varsa bu gözlemlerin hangi sınıfta yer alacağı belli değildir ve sınıflama yapıldığında bu değerler dışarıda kalır.

Eğer virgülden sonra basamak varsa sınıflama işlemi yapılırken virgülden sonraki haneler dikkate alınmalıdır. Örneğin bu sınıflandırma aşağıdaki gibi yapılabilir. 20, 0 -24, 9 25, 0 -29, 9 30, 0 -34, 9

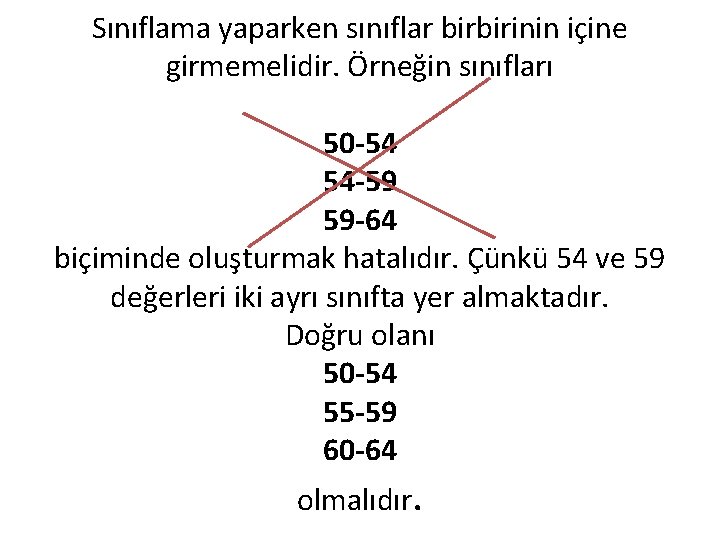
Sınıflama yaparken sınıflar birbirinin içine girmemelidir. Örneğin sınıfları 50 -54 54 -59 59 -64 biçiminde oluşturmak hatalıdır. Çünkü 54 ve 59 değerleri iki ayrı sınıfta yer almaktadır. Doğru olanı 50 -54 55 -59 60 -64 olmalıdır.

Sınıf aralıklarının birbirine eşit şekilde düzenlenmesi, istatistiksel çözümlemede kolaylık sağlar. Ancak gerektiğinde sınıf aralıkları eşit olmayabilir. Dağılım hakkında yeterli bilgiye sahip olabilmek için oluşturulacak sınıf sayısının 8 -15 arasında olması önerilmektedir. Sınıf sayısının az olması dağılım hakkında ayrıntılı bilgi elde etmemize engel olur.

Örnek : Canlı ağırlık için 25 koyuna ilişkin verileri sınıflandıralım Canlı ağırlık verilerinde En Küçük Değer (EKD)=21. 3 En Büyük Değer (EBD)=32. 4 ‘tür Dağılım Aralığı (DA) bulunur. Bu örnek için DA = EBD-EKD = 11. 1’dir.

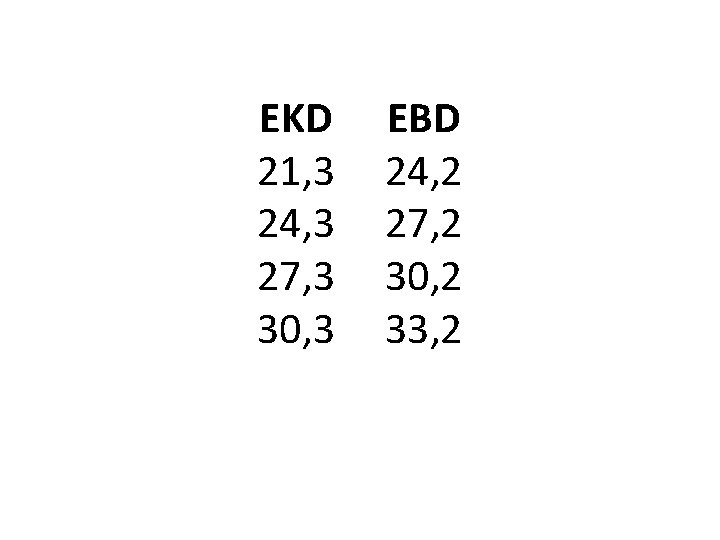
Dağılım aralığı değeri belirlediğimiz sınıf sayısına bölünerek sınıf aralığı (C) bulunur. Örneğin veriyi 4 sınıfta toplamak istersek C=11, 1/4=2, 75 3 olur. (Sonuç tamsayı olacağı için yuvarlama yapılır). Buna Göre sınıflar, dağılımdaki en küçük değerden başlamak üzere aşağıdaki gibi oluşturulur.

EKD 21, 3 24, 3 27, 3 30, 3 EBD 24, 2 27, 2 30, 2 33, 2

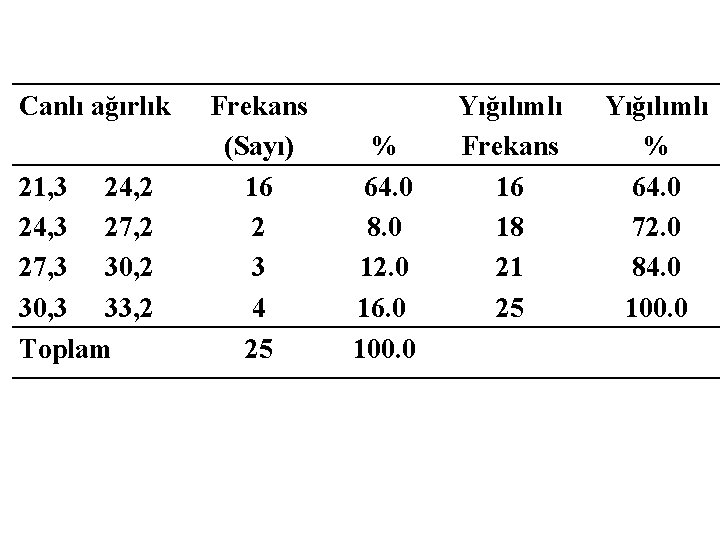
Daha sonra her sınıfa düşen frekanslar 1 no’lu hayvandan başlamak üzere çeteleme yapılır ve sayısı yazılır. Canlı ağırlık 21, 3 24, 2 24, 3 27, 2 27, 3 30, 2 30, 3 33, 2 Çetele Sayı //////// // //// 16 2 3 4

Canlı ağırlık 21, 3 24, 2 24, 3 27, 2 27, 3 30, 2 30, 3 33, 2 Toplam Frekans (Sayı) 16 2 3 4 25 % 64. 0 8. 0 12. 0 16. 0 100. 0 Yığılımlı Frekans 16 18 21 25 Yığılımlı % 64. 0 72. 0 84. 0 100. 0

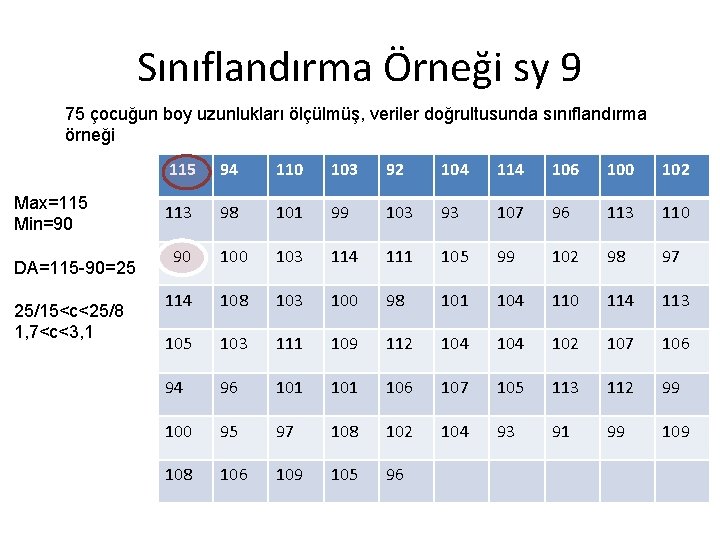
Sınıflandırma Örneği sy 9 75 çocuğun boy uzunlukları ölçülmüş, veriler doğrultusunda sınıflandırma örneği Max=115 Min=90 DA=115 -90=25 25/15<c<25/8 1, 7<c<3, 1 115 94 110 103 92 104 114 106 100 102 113 98 101 99 103 93 107 96 113 110 90 103 114 111 105 99 102 98 97 114 108 103 100 98 101 104 110 114 113 105 103 111 109 112 104 102 107 106 94 96 101 106 107 105 113 112 99 100 95 97 108 102 104 93 91 99 108 106 109 105 96

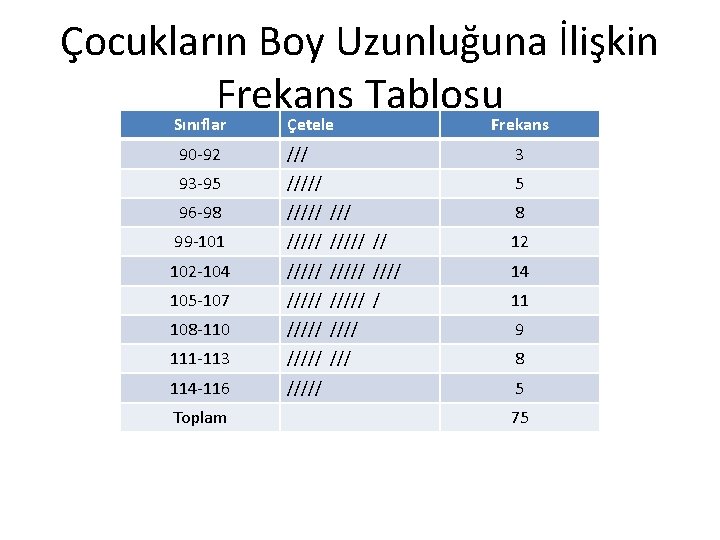
Çocukların Boy Uzunluğuna İlişkin Frekans Tablosu Sınıflar Çetele 90 -92 /// 3 93 -95 ///// 5 96 -98 ///// 8 99 -101 ///// // 12 102 -104 ///// 14 105 -107 ///// / 11 108 -110 ///// 9 111 -113 ///// 8 114 -116 ///// 5 Toplam Frekans 75