SAT MATHEMATICS LINES INTERSECTIONS ANGLES What you gain

SAT MATHEMATICS LINES, INTERSECTIONS & ANGLES

What you gain after studying this course fter a r e answ past n a c AT you S s d n a o i wnlo uest o q D e ( h of t rse. e u on ds/) o m a s c r o o l e S e n h answ /sat-dow ng t i d y n d a u st pers cksat. net a p exam ww. cra 014 //w : 2 p y t t a h M 2, 17 SAT – 4 ction – 13 14 e 0 2 S e Jun e on 7 3, 10, 16 n i t o c N e SAT S 9– n 3 – 14 n o i o t i c t Se Sec – 2, 4 n o 9 013 , 2 3 Secti r – e ctob on 6 i O t c T e S SA – 14 4 n o ecti 14 S 0 2 7– 9 n a n J o i 8 T t 1 SA Sec - 8. 3 8 -3 n n o i o t i c t Se 14 Sec – 7 n o 3, 13 Secti – 1 1 on Secti The course covers the relationship between angles and straight lines. This extends up to the properties of triangles, quadrilaterals and polygons. There are three maths sections in SAT and has 54 questions in total. The students will be able to answer 3 – 7 questions when this course is completed.

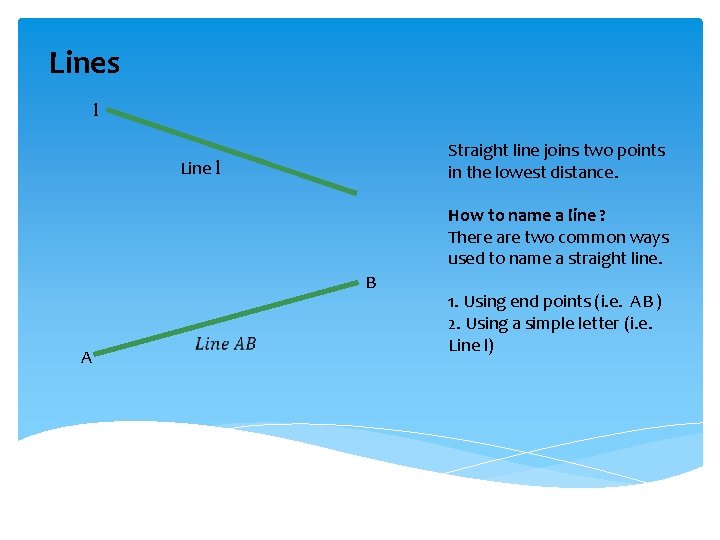
Lines l Straight line joins two points in the lowest distance. Line l How to name a line ? There are two common ways used to name a straight line. B A 1. Using end points (i. e. AB ) 2. Using a simple letter (i. e. Line l)

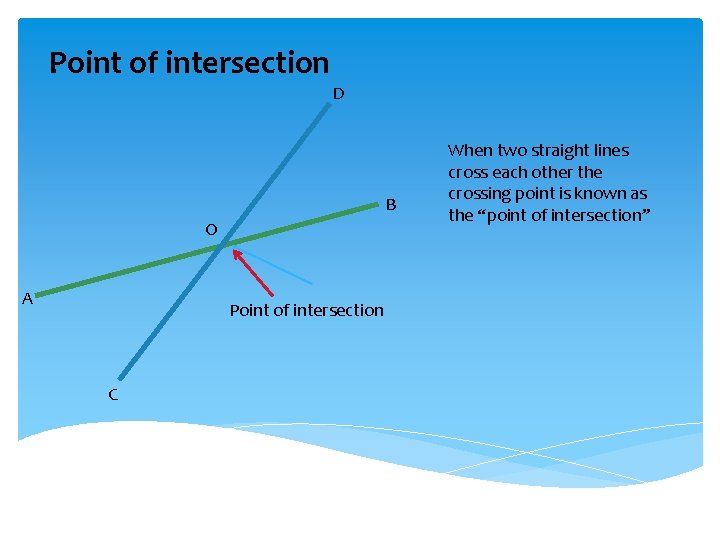
Point of intersection D B O A Point of intersection C When two straight lines cross each other the crossing point is known as the “point of intersection”

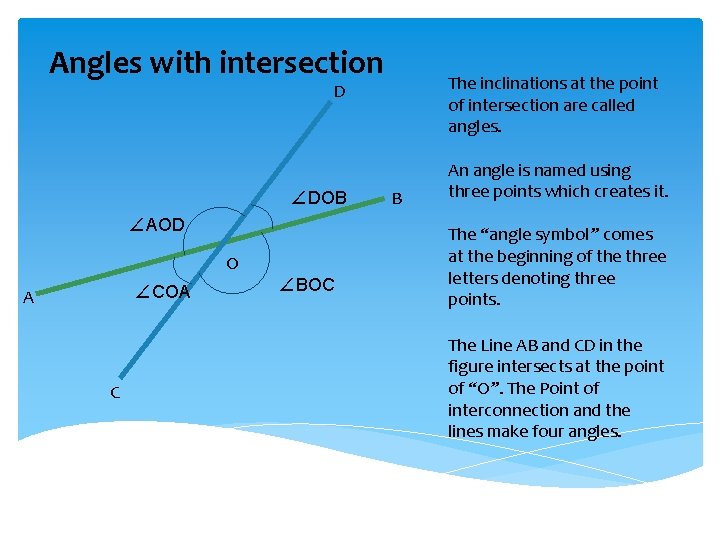
Angles with intersection The inclinations at the point of intersection are called angles. D ∠DOB ∠AOD O ∠COA A C ∠BOC B An angle is named using three points which creates it. The “angle symbol” comes at the beginning of the three letters denoting three points. The Line AB and CD in the figure intersects at the point of “O”. The Point of interconnection and the lines make four angles.

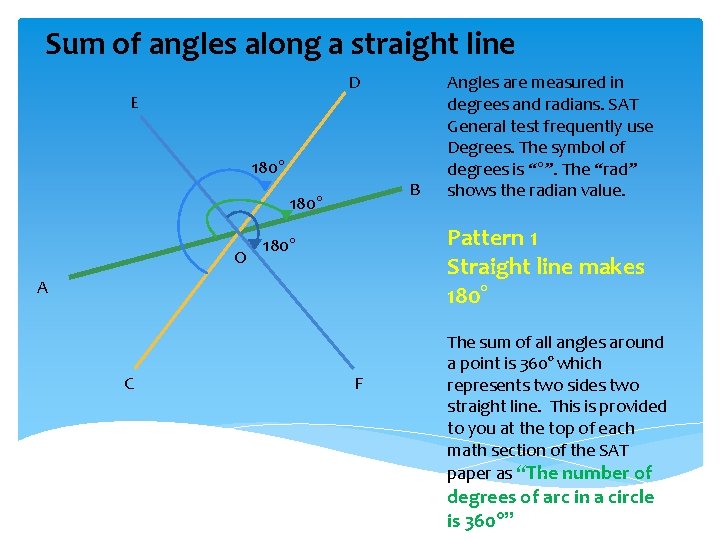
Sum of angles along a straight line D E 180° B 180° O Pattern 1 Straight line makes 180° A C Angles are measured in degrees and radians. SAT General test frequently use Degrees. The symbol of degrees is “°”. The “rad” shows the radian value. F The sum of all angles around a point is 360° which represents two sides two straight line. This is provided to you at the top of each math section of the SAT paper as “The number of degrees of arc in a circle is 360°”

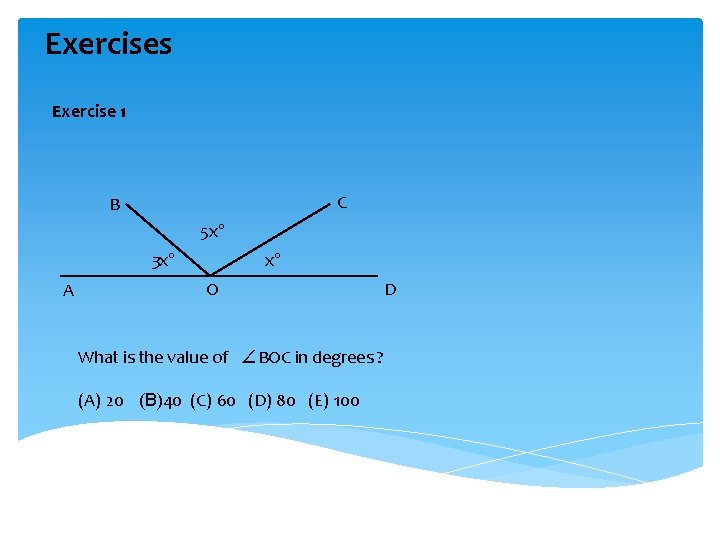
Exercises Exercise 1 C B 5 x° x° 3 x° A O What is the value of ∠BOC in degrees ? (A) 20 (B)40 (C) 60 (D) 80 (E) 100 D

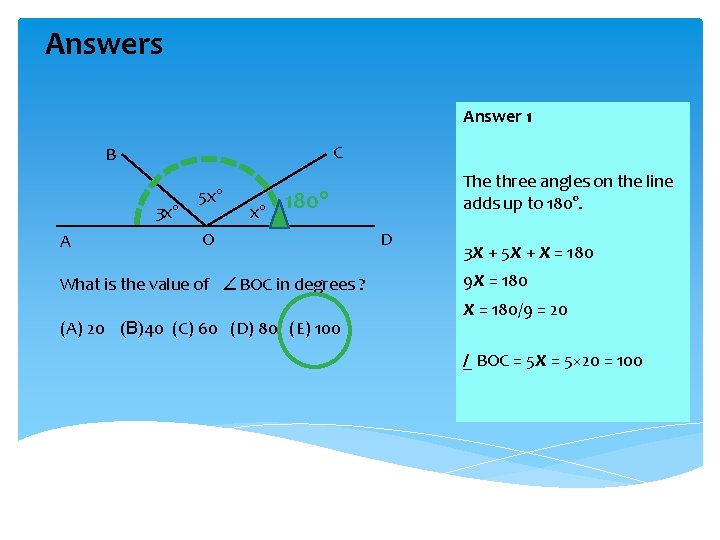
Answers Answer 1 C B 3 x° A 5 x° x° The three angles on the line adds up to 180° O What is the value of ∠BOC in degrees ? (A) 20 (B)40 (C) 60 (D) 80 (E) 100 D 3 x + 5 x + x = 180 9 x = 180/9 = 20 /_ BOC = 5 x = 5× 20 = 100

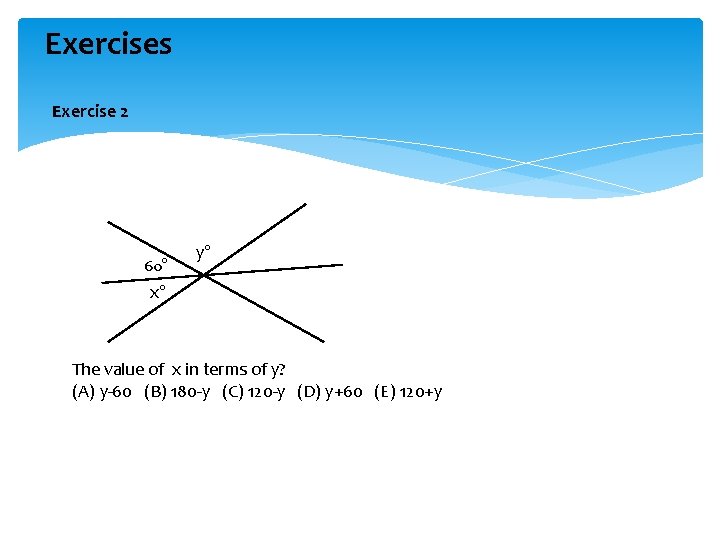
Exercises Exercise 2 60° y° x° The value of x in terms of y? (A) y-60 (B) 180 -y (C) 120 -y (D) y+60 (E) 120+y

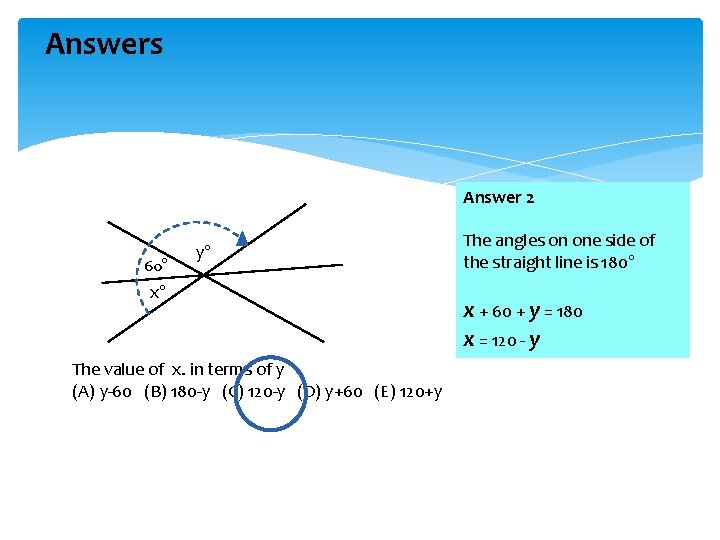
Answers Answer 2 60° y° x° The value of x. in terms of y (A) y-60 (B) 180 -y (C) 120 -y (D) y+60 (E) 120+y The angles on one side of the straight line is 180° x + 60 + y = 180 x = 120 - y

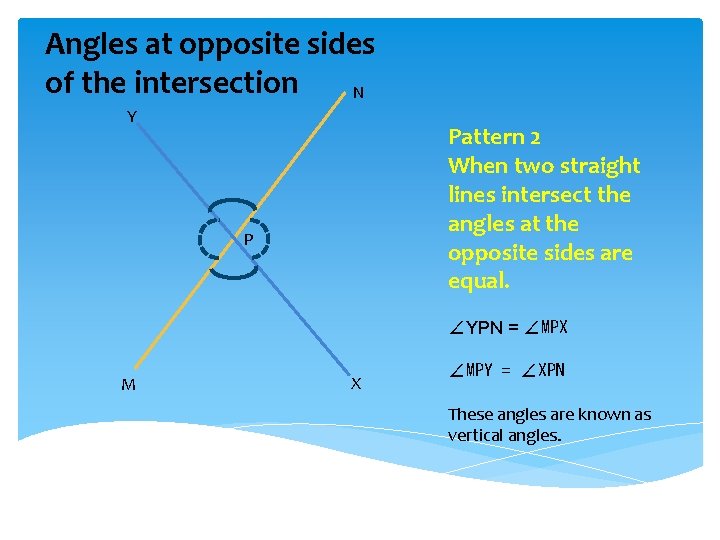
Angles at opposite sides of the intersection N Y Pattern 2 When two straight lines intersect the angles at the opposite sides are equal. P ∠YPN = ∠MPX M X ∠MPY = ∠XPN These angles are known as vertical angles.

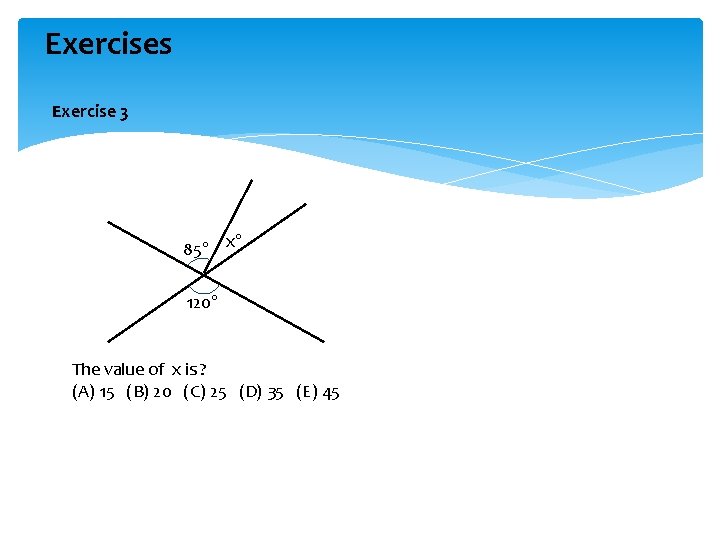
Exercises Exercise 3 85° x° 120° The value of x is ? (A) 15 (B) 20 (C) 25 (D) 35 (E) 45

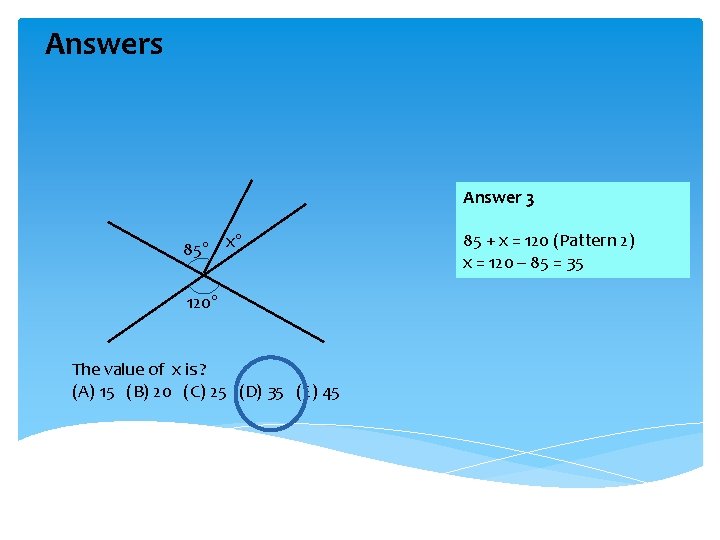
Answers Answer 3 85° x° 120° The value of x is ? (A) 15 (B) 20 (C) 25 (D) 35 (E) 45 85 + x = 120 (Pattern 2) x = 120 – 85 = 35

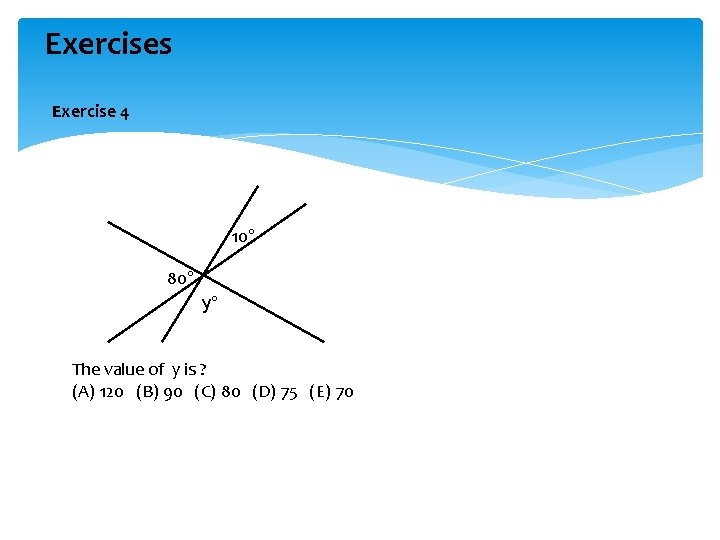
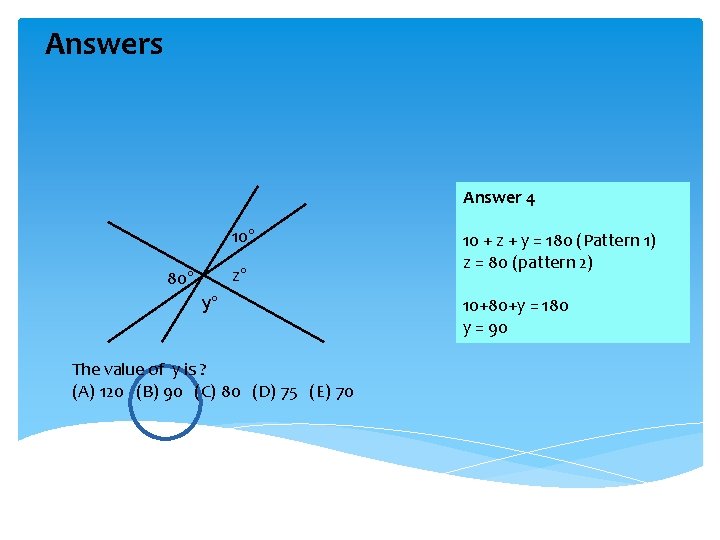
Exercises Exercise 4 10° 80° y° The value of y is ? (A) 120 (B) 90 (C) 80 (D) 75 (E) 70

Answers Answer 4 10° z° 80° y° The value of y is ? (A) 120 (B) 90 (C) 80 (D) 75 (E) 70 10 + z + y = 180 (Pattern 1) z = 80 (pattern 2) 10+80+y = 180 y = 90

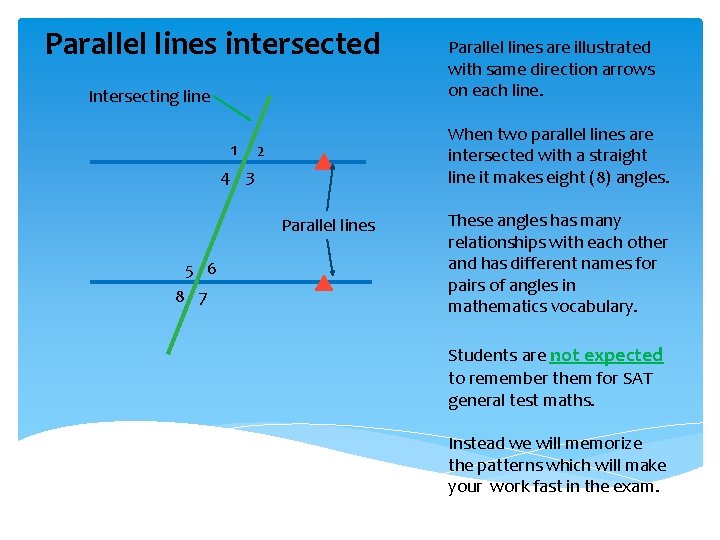
Parallel lines intersected Intersecting line 1 When two parallel lines are intersected with a straight line it makes eight (8) angles. 2 4 3 Parallel lines 5 6 8 7 Parallel lines are illustrated with same direction arrows on each line. These angles has many relationships with each other and has different names for pairs of angles in mathematics vocabulary. Students are not expected to remember them for SAT general test maths. Instead we will memorize the patterns which will make your work fast in the exam.

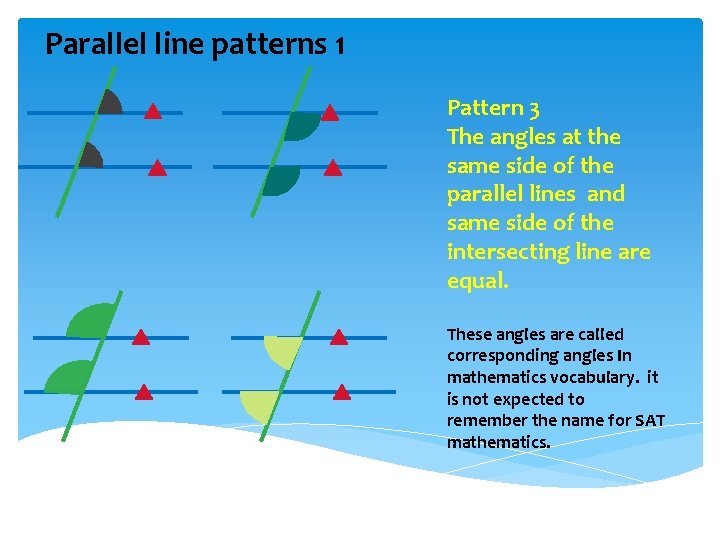
Parallel line patterns 1 Pattern 3 The angles at the same side of the parallel lines and same side of the intersecting line are equal. These angles are called corresponding angles In mathematics vocabulary. it is not expected to remember the name for SAT mathematics.

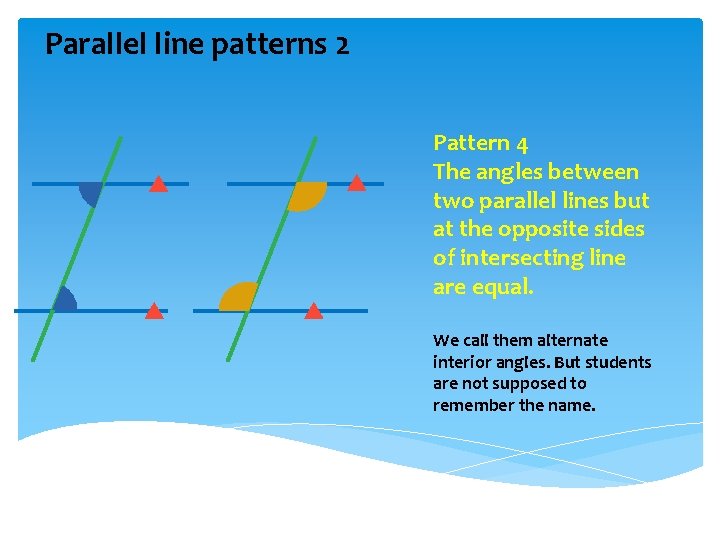
Parallel line patterns 2 Pattern 4 The angles between two parallel lines but at the opposite sides of intersecting line are equal. We call them alternate interior angles. But students are not supposed to remember the name.

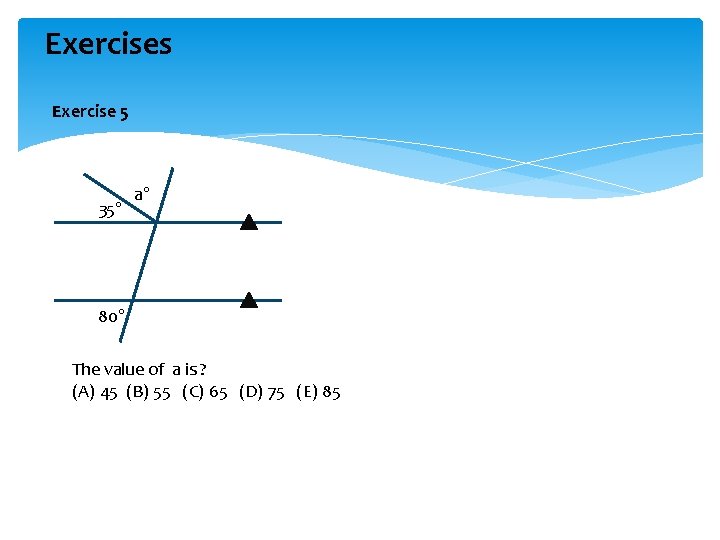
Exercises Exercise 5 35° a° 80° The value of a is ? (A) 45 (B) 55 (C) 65 (D) 75 (E) 85

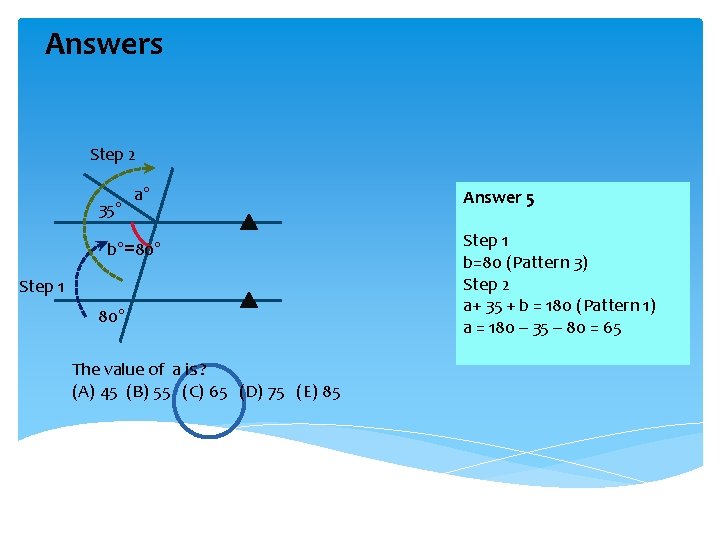
Answers Step 2 35° a° b°=80° Step 1 80° The value of a is ? (A) 45 (B) 55 (C) 65 (D) 75 (E) 85 Answer 5 Step 1 b=80 (Pattern 3) Step 2 a+ 35 + b = 180 (Pattern 1) a = 180 – 35 – 80 = 65

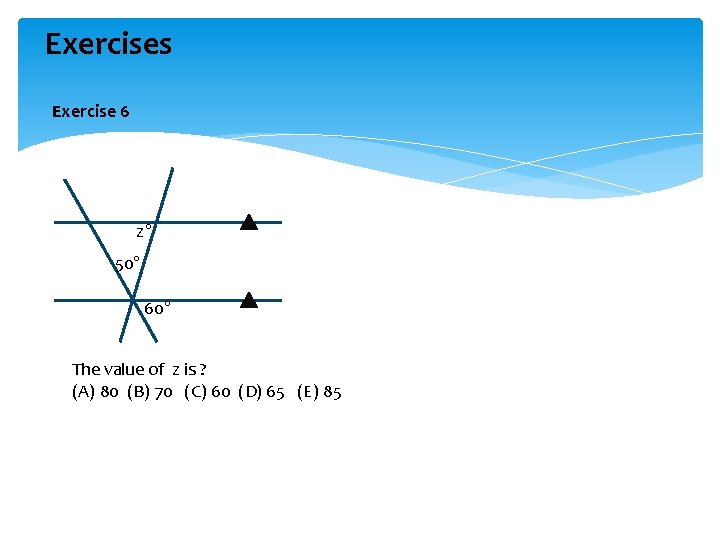
Exercises Exercise 6 z° 50° 60° The value of z is ? (A) 80 (B) 70 (C) 60 (D) 65 (E) 85

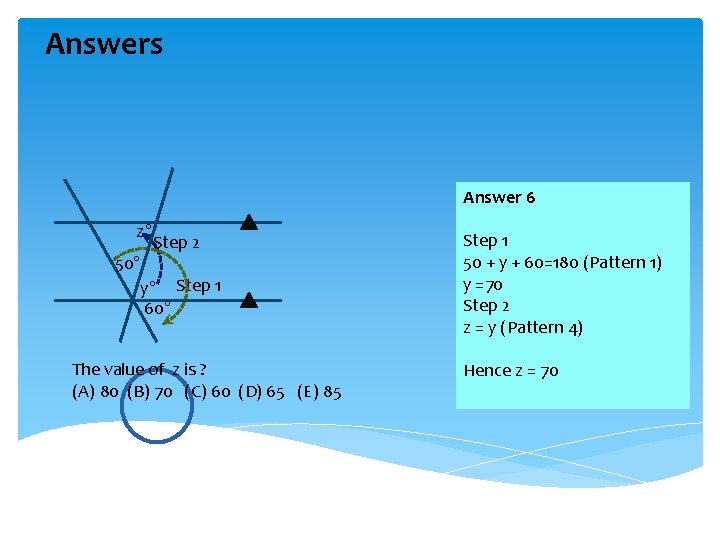
Answers Answer 6 z° Step 2 50° y° Step 1 60° The value of z is ? (A) 80 (B) 70 (C) 60 (D) 65 (E) 85 Step 1 50 + y + 60=180 (Pattern 1) y =70 Step 2 z = y (Pattern 4) Hence z = 70

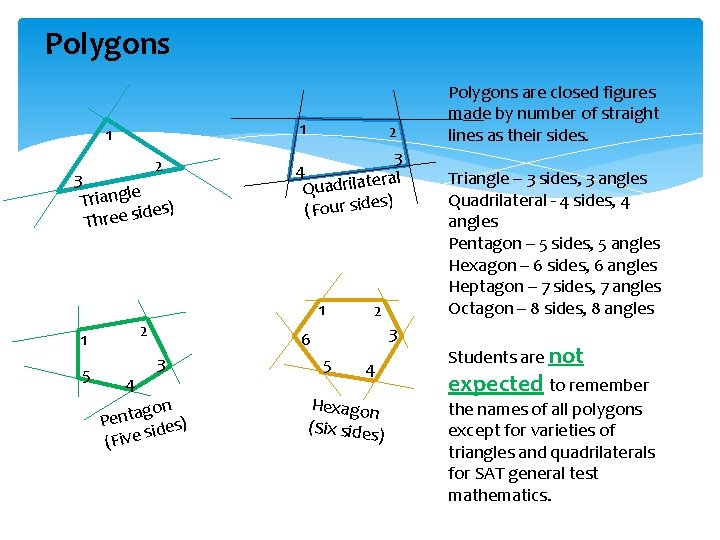
Polygons 1 1 2 3 e Triangl ides) s e e r h T 5 1 2 1 4 2 3 4 ral Quadrilate s) (Four side 2 3 6 3 on g a t n Pe es) d i s e v (Fi 5 4 Hexagon (Six sides ) Polygons are closed figures made by number of straight lines as their sides. Triangle – 3 sides, 3 angles Quadrilateral - 4 sides, 4 angles Pentagon – 5 sides, 5 angles Hexagon – 6 sides, 6 angles Heptagon – 7 sides, 7 angles Octagon – 8 sides, 8 angles Students are not expected to remember the names of all polygons except for varieties of triangles and quadrilaterals for SAT general test mathematics.

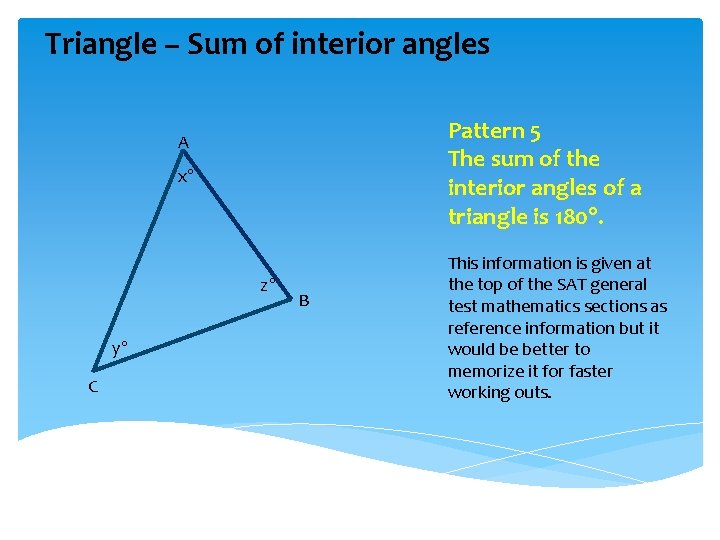
Triangle – Sum of interior angles Pattern 5 The sum of the interior angles of a triangle is 180°. A x° z° y° C B This information is given at the top of the SAT general test mathematics sections as reference information but it would be better to memorize it for faster working outs.

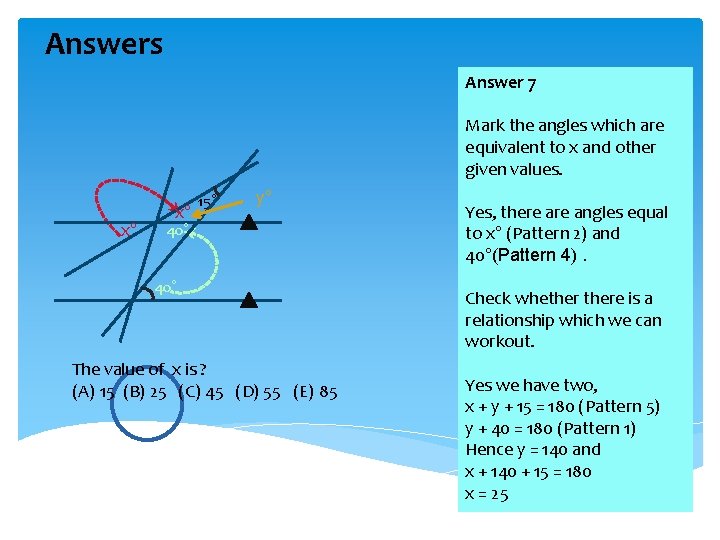
Exercises Exercise 7 15° x° 40° The value of x is ? (A) 15 (B) 25 (C) 45 (D) 55 (E) 85

Answers Answer 7 Mark the angles which are equivalent to x and other given values. x° x° 15° y° 40° The value of x is ? (A) 15 (B) 25 (C) 45 (D) 55 (E) 85 Yes, there angles equal to x° (Pattern 2) and 40°(Pattern 4). Check whethere is a relationship which we can workout. Yes we have two, x + y + 15 = 180 (Pattern 5) y + 40 = 180 (Pattern 1) Hence y = 140 and x + 140 + 15 = 180 x = 25

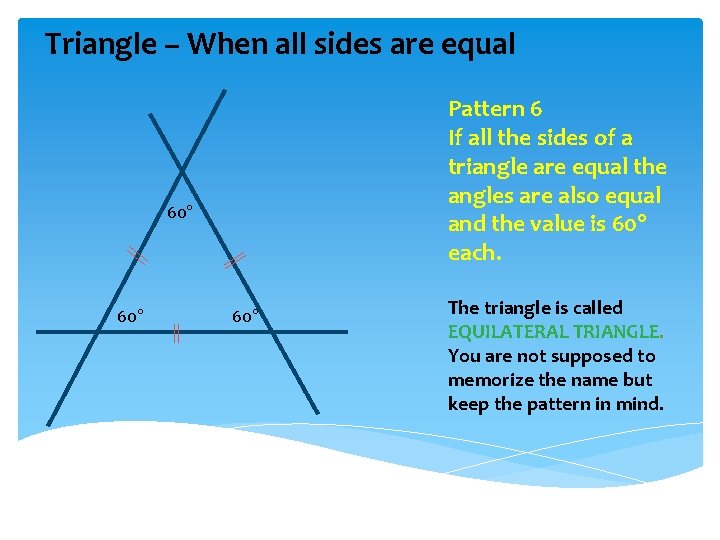
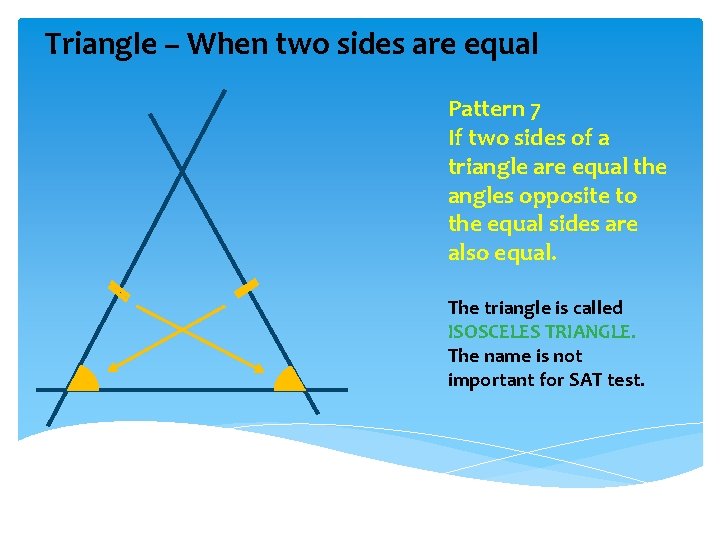
Triangle – When all sides are equal Pattern 6 If all the sides of a triangle are equal the angles are also equal and the value is 60° each. 60° 60° The triangle is called EQUILATERAL TRIANGLE. You are not supposed to memorize the name but keep the pattern in mind.

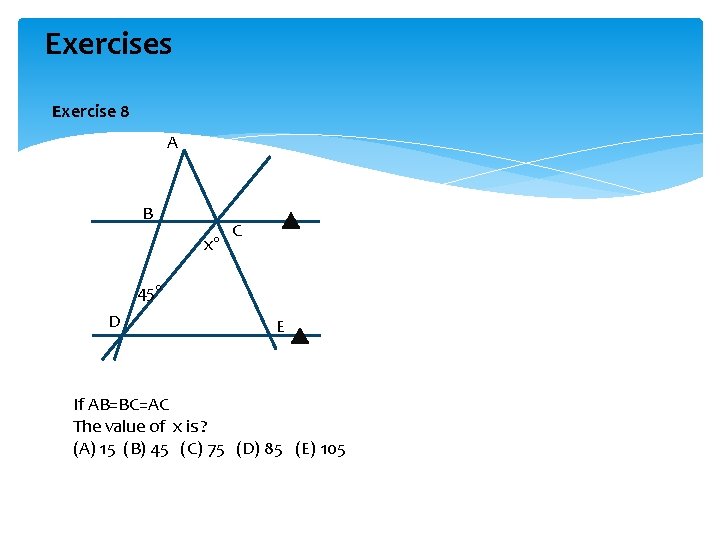
Exercises Exercise 8 A B x° C 45° D E If AB=BC=AC The value of x is ? (A) 15 (B) 45 (C) 75 (D) 85 (E) 105

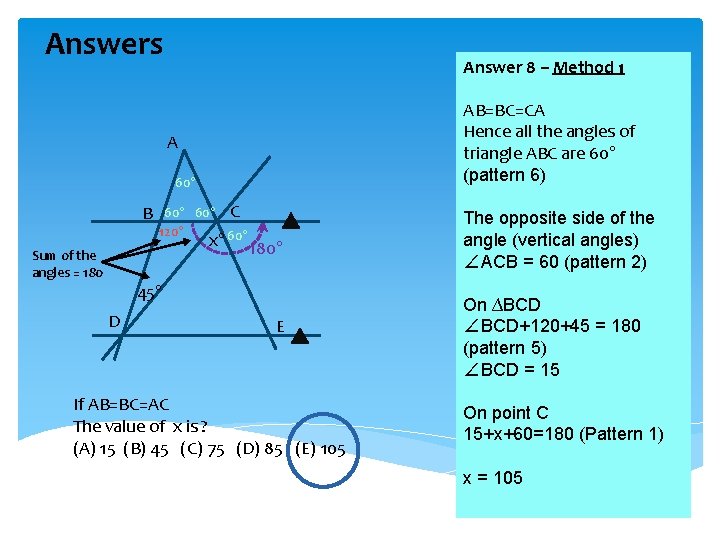
Answers Answer 8 – Method 1 AB=BC=CA Hence all the angles of triangle ABC are 60° (pattern 6) A 60° B Sum of the angles = 180 60° C 120° x° 60° 180° 45° D E If AB=BC=AC The value of x is ? (A) 15 (B) 45 (C) 75 (D) 85 (E) 105 The opposite side of the angle (vertical angles) ∠ACB = 60 (pattern 2) On ∆BCD ∠BCD+120+45 = 180 (pattern 5) ∠BCD = 15 On point C 15+x+60=180 (Pattern 1) x = 105

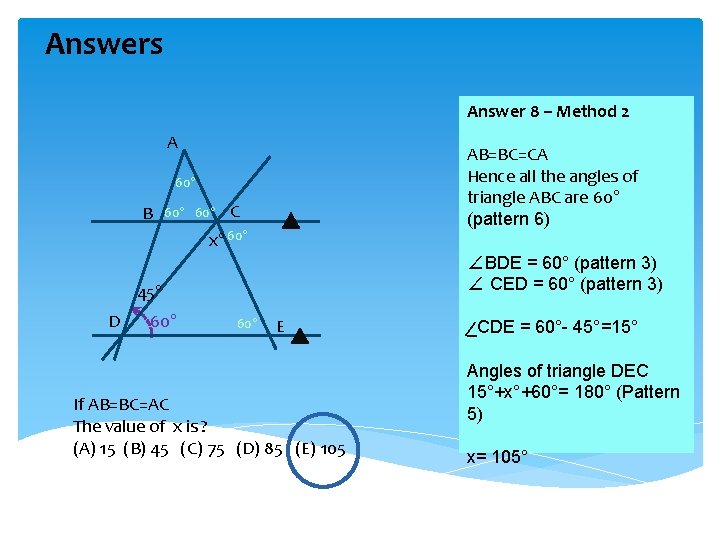
Answers Answer 8 – Method 2 A AB=BC=CA Hence all the angles of triangle ABC are 60° (pattern 6) 60° B 60° C x° 60° ∠BDE = 60° (pattern 3) ∠ CED = 60° (pattern 3) 45° D 60° E If AB=BC=AC The value of x is ? (A) 15 (B) 45 (C) 75 (D) 85 (E) 105 _CDE = 60°- 45°=15° ⁄ Angles of triangle DEC 15°+x°+60°= 180° (Pattern 5) x= 105°

Triangle – When two sides are equal Pattern 7 If two sides of a triangle are equal the angles opposite to the equal sides are also equal. The triangle is called ISOSCELES TRIANGLE. The name is not important for SAT test.

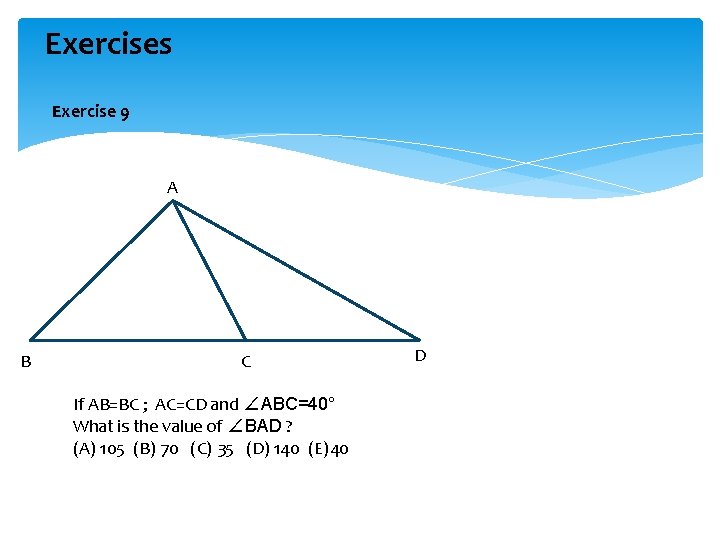
Exercises Exercise 9 A B C If AB=BC ; AC=CD and ∠ABC=40° What is the value of ∠BAD ? (A) 105 (B) 70 (C) 35 (D) 140 (E)40 D

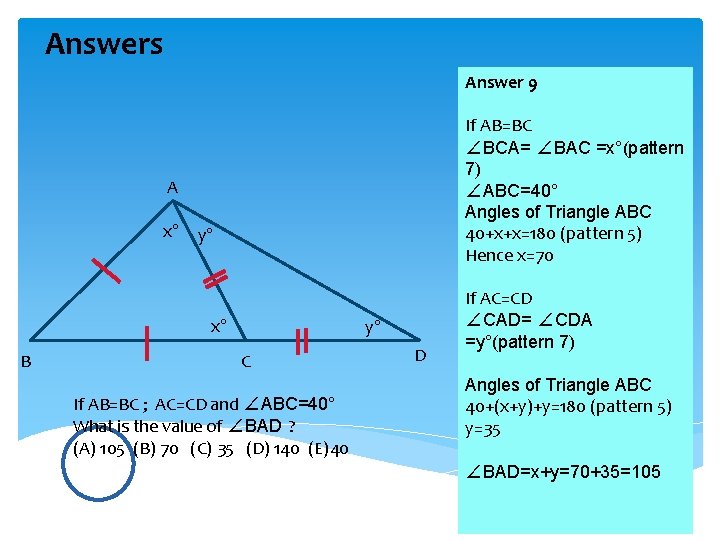
Answers Answer 9 If AB=BC ∠BCA= ∠BAC =x°(pattern 7) ∠ABC=40° Angles of Triangle ABC 40+x+x=180 (pattern 5) Hence x=70 A x° y° x° B y° C If AB=BC ; AC=CD and ∠ABC=40° What is the value of ∠BAD ? (A) 105 (B) 70 (C) 35 (D) 140 (E)40 D If AC=CD ∠CAD= ∠CDA =y°(pattern 7) Angles of Triangle ABC 40+(x+y)+y=180 (pattern 5) y=35 ∠BAD=x+y=70+35=105

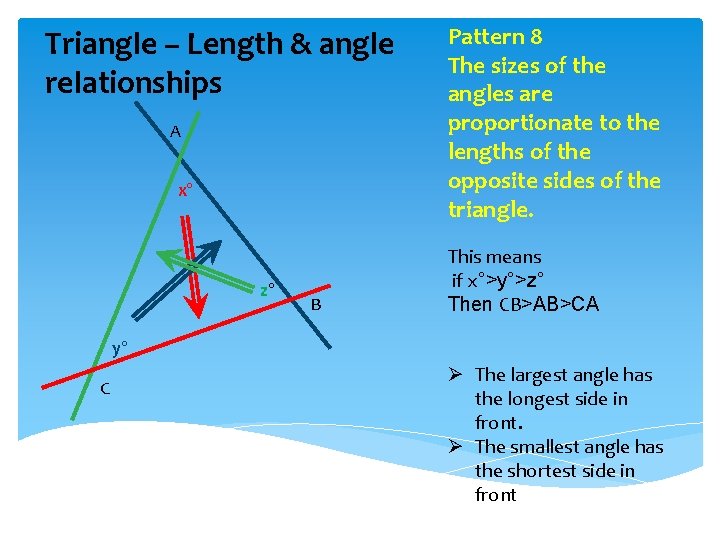
Triangle – Length & angle relationships A x° z° B Pattern 8 The sizes of the angles are proportionate to the lengths of the opposite sides of the triangle. This means if x°>y°>z° Then CB>AB>CA y° C Ø The largest angle has the longest side in front. Ø The smallest angle has the shortest side in front

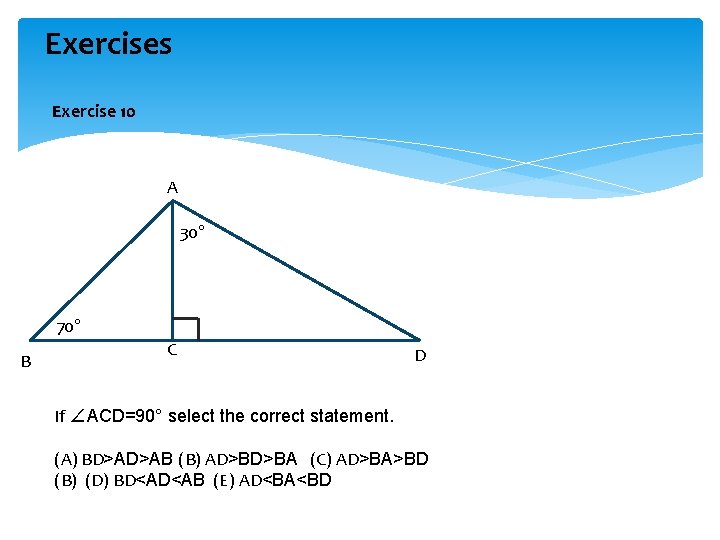
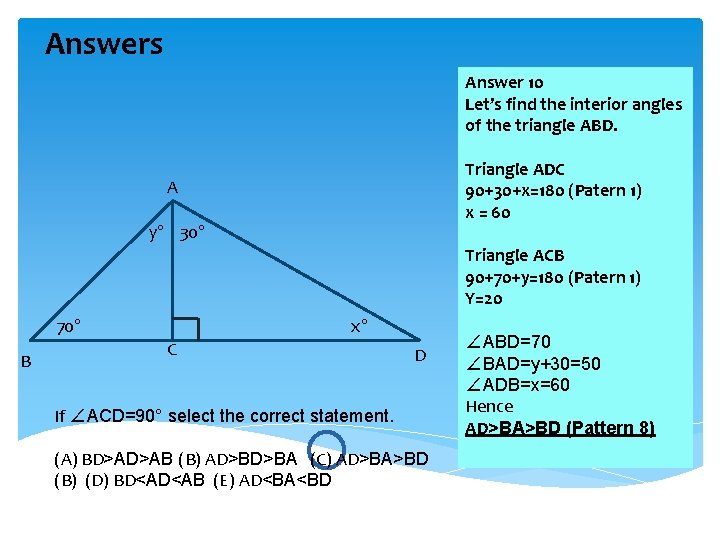
Exercises Exercise 10 A 30° 70° B C D If ∠ACD=90° select the correct statement. (A) BD>AD>AB (B) AD>BD>BA (C) AD>BA>BD (B) (D) BD<AD<AB (E) AD<BA<BD

Answers Answer 10 Let’s find the interior angles of the triangle ABD. Triangle ADC 90+30+x=180 (Patern 1) x = 60 A y° 30° Triangle ACB 90+70+y=180 (Patern 1) Y=20 x° 70° B C D If ∠ACD=90° select the correct statement. (A) BD>AD>AB (B) AD>BD>BA (C) AD>BA>BD (B) (D) BD<AD<AB (E) AD<BA<BD ∠ABD=70 ∠BAD=y+30=50 ∠ADB=x=60 Hence AD>BA>BD (Pattern 8)

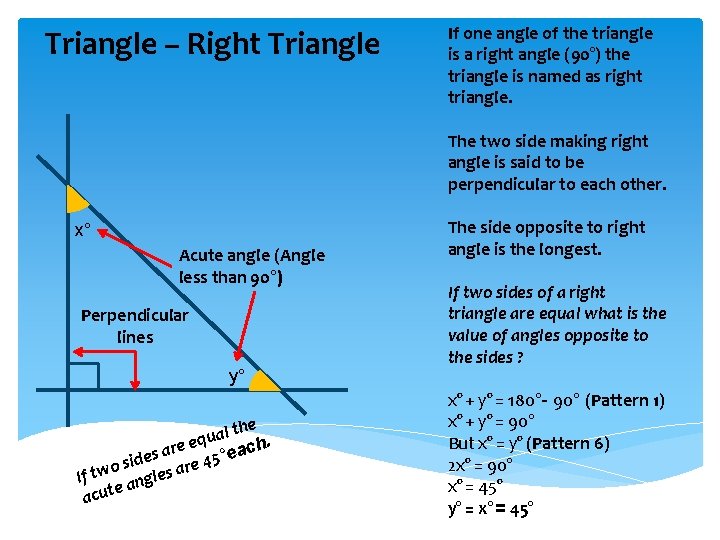
Triangle – Right Triangle If one angle of the triangle is a right angle (90°) the triangle is named as right triangle. The two side making right angle is said to be perpendicular to each other. x° Acute angle (Angle less than 90°) Perpendicular lines y° the l a u eq h. e c r a a e ides are 45° s o If tw angles e acut The side opposite to right angle is the longest. If two sides of a right triangle are equal what is the value of angles opposite to the sides ? x° + y° = 180°- 90° (Pattern 1) x° + y° = 90° But x° = y° (Pattern 6) 2 x° = 90° x° = 45° y° = x°= 45°

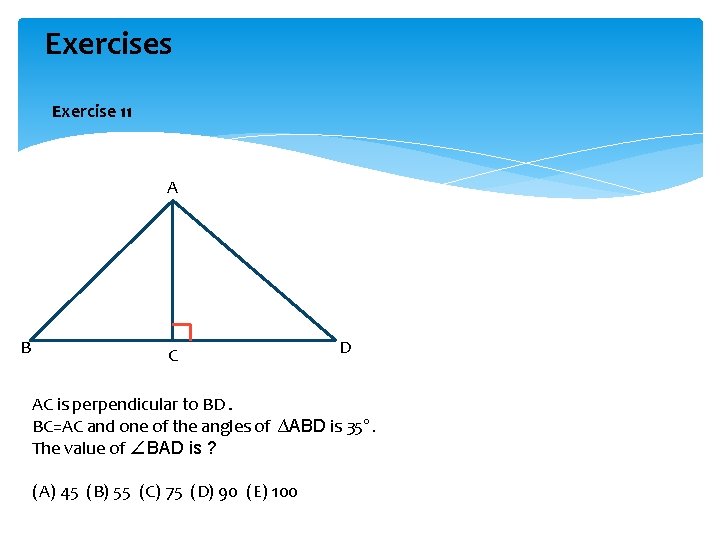
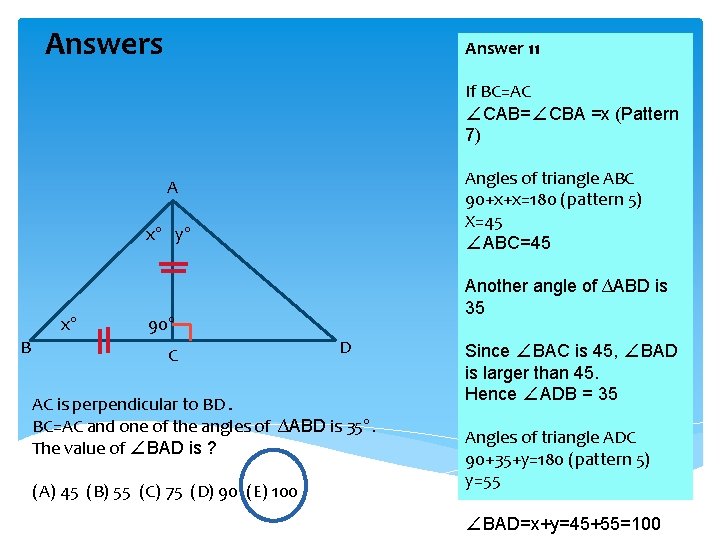
Exercises Exercise 11 A B C D AC is perpendicular to BD. BC=AC and one of the angles of ∆ABD is 35°. The value of ∠BAD is ? (A) 45 (B) 55 (C) 75 (D) 90 (E) 100

Answers Answer 11 If BC=AC ∠CAB=∠CBA =x (Pattern 7) Angles of triangle ABC 90+x+x=180 (pattern 5) X=45 ∠ABC=45 A x° y° x° B Another angle of ∆ABD is 35 90° C D AC is perpendicular to BD. BC=AC and one of the angles of ∆ABD is 35°. The value of ∠BAD is ? (A) 45 (B) 55 (C) 75 (D) 90 (E) 100 Since ∠BAC is 45, ∠BAD is larger than 45. Hence ∠ADB = 35 Angles of triangle ADC 90+35+y=180 (pattern 5) y=55 ∠BAD=x+y=45+55=100

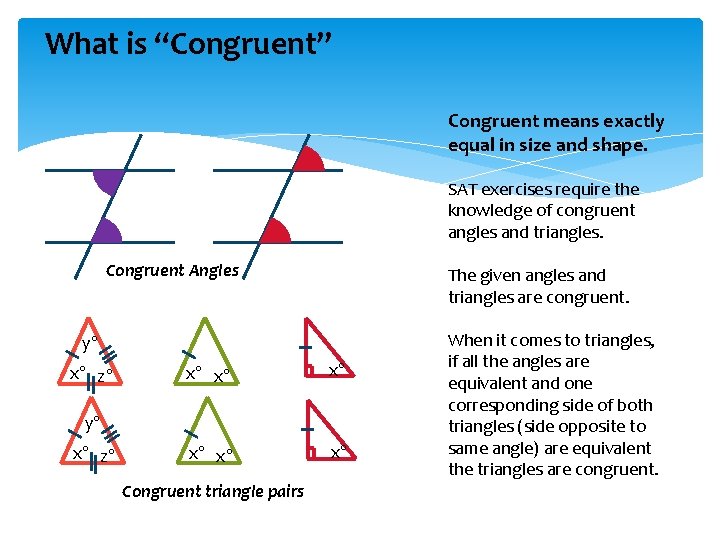
What is “Congruent” Congruent means exactly equal in size and shape. SAT exercises require the knowledge of congruent angles and triangles. Congruent Angles The given angles and triangles are congruent. y° x° z° x° x° x° y° x° z° Congruent triangle pairs When it comes to triangles, if all the angles are equivalent and one corresponding side of both triangles (side opposite to same angle) are equivalent the triangles are congruent.

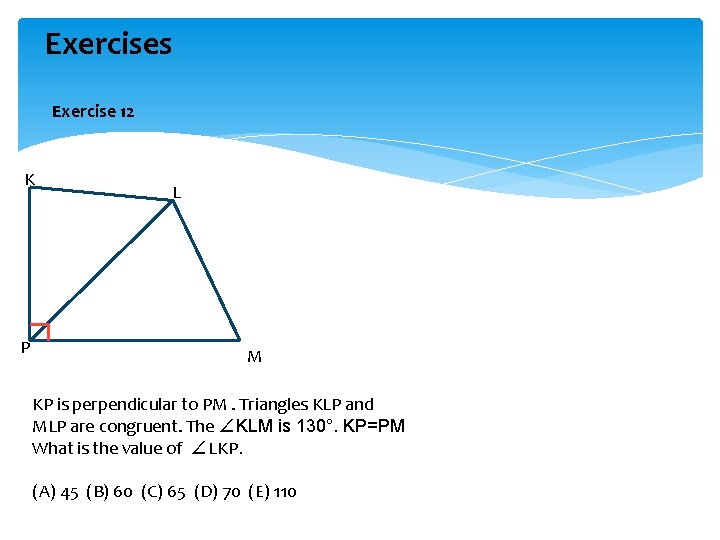
Exercises Exercise 12 K P L M KP is perpendicular to PM. Triangles KLP and MLP are congruent. The ∠KLM is 130°. KP=PM What is the value of ∠LKP. (A) 45 (B) 60 (C) 65 (D) 70 (E) 110

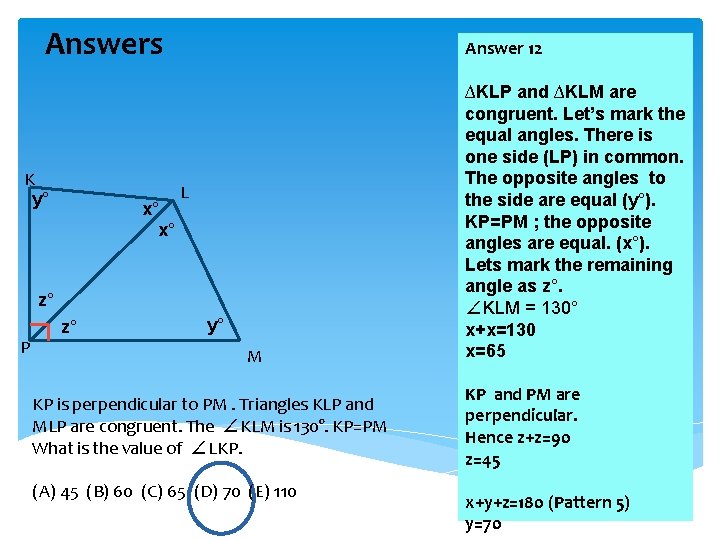
Answers K y° x° x° Answer 12 L z° P z° y° M KP is perpendicular to PM. Triangles KLP and MLP are congruent. The ∠KLM is 130°. KP=PM What is the value of ∠LKP. (A) 45 (B) 60 (C) 65 (D) 70 (E) 110 ∆KLP and ∆KLM are congruent. Let’s mark the equal angles. There is one side (LP) in common. The opposite angles to the side are equal (y°). KP=PM ; the opposite angles are equal. (x°). Lets mark the remaining angle as z°. ∠KLM = 130° x+x=130 x=65 KP and PM are perpendicular. Hence z+z=90 z=45 x+y+z=180 (Pattern 5) y=70

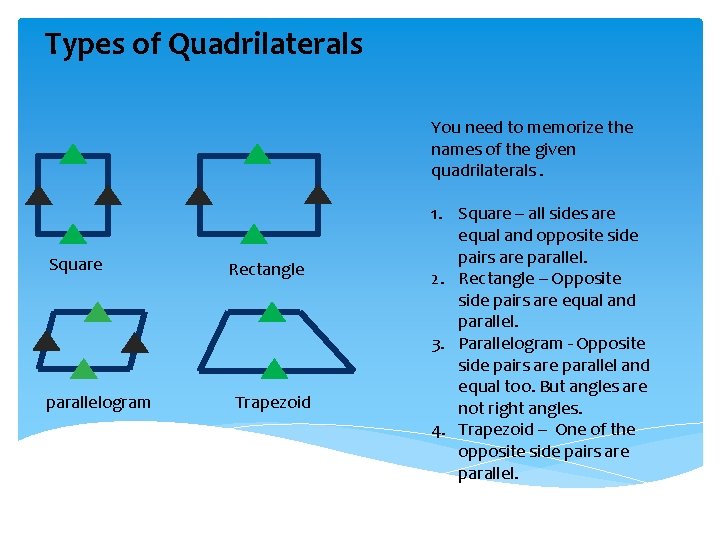
Types of Quadrilaterals You need to memorize the names of the given quadrilaterals. Square parallelogram Rectangle Trapezoid 1. Square – all sides are equal and opposite side pairs are parallel. 2. Rectangle – Opposite side pairs are equal and parallel. 3. Parallelogram - Opposite side pairs are parallel and equal too. But angles are not right angles. 4. Trapezoid – One of the opposite side pairs are parallel.

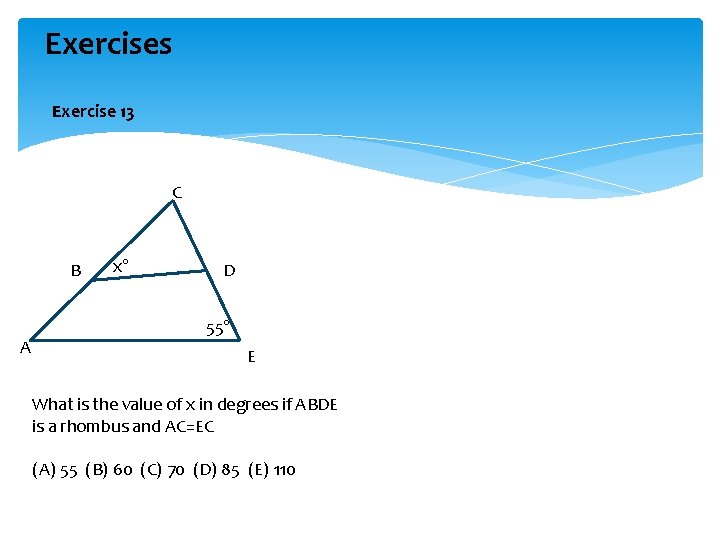
Exercises Exercise 13 C B A x° D 55° E What is the value of x in degrees if ABDE is a rhombus and AC=EC (A) 55 (B) 60 (C) 70 (D) 85 (E) 110

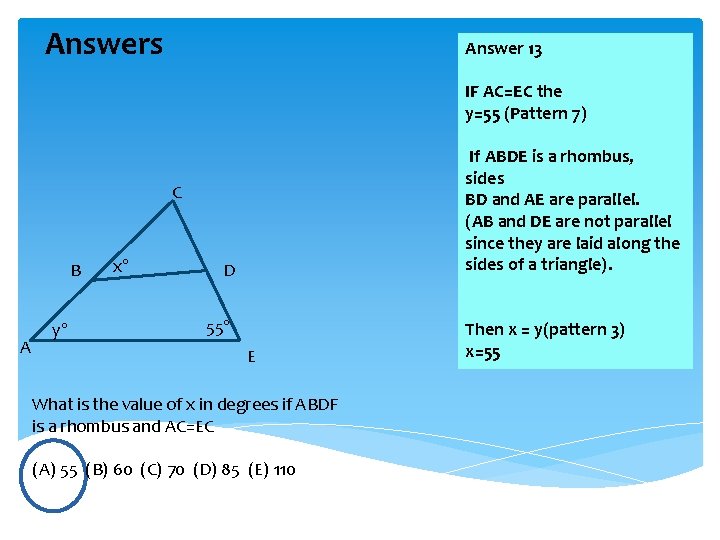
Answers Answer 13 IF AC=EC the y=55 (Pattern 7) If ABDE is a rhombus, sides BD and AE are parallel. (AB and DE are not parallel since they are laid along the sides of a triangle). C B A y° x° D 55° E What is the value of x in degrees if ABDF is a rhombus and AC=EC (A) 55 (B) 60 (C) 70 (D) 85 (E) 110 Then x = y(pattern 3) x=55

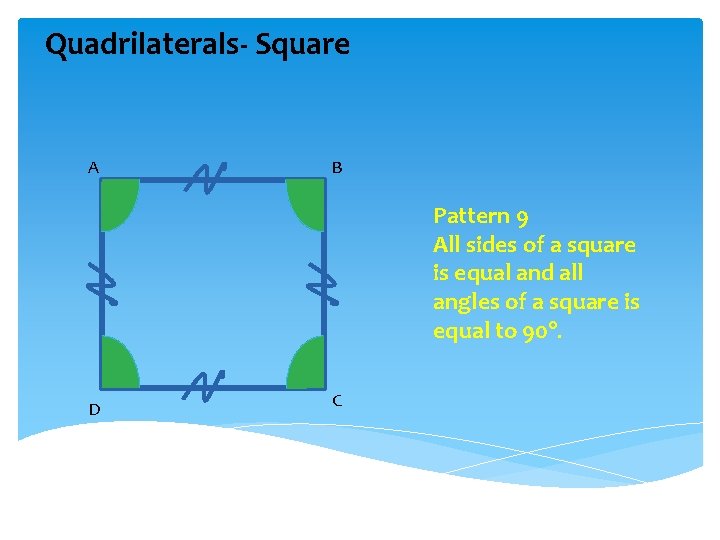
Quadrilaterals- Square A B Pattern 9 All sides of a square is equal and all angles of a square is equal to 90°. D C

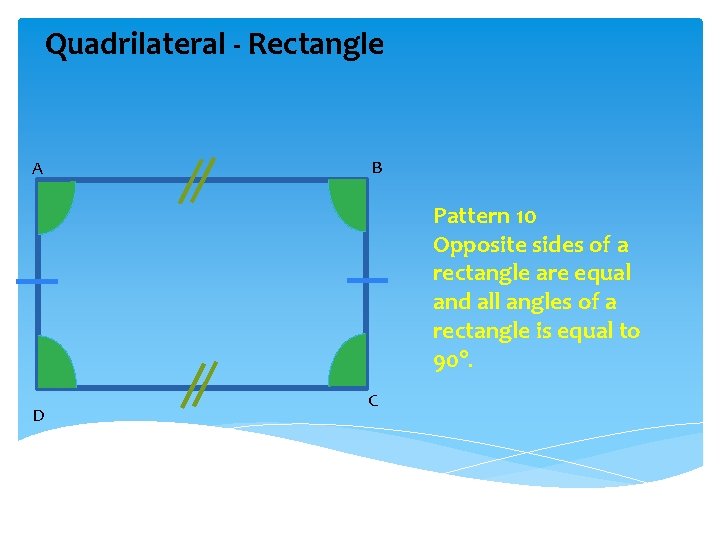
Quadrilateral - Rectangle A B Pattern 10 Opposite sides of a rectangle are equal and all angles of a rectangle is equal to 90°. D C

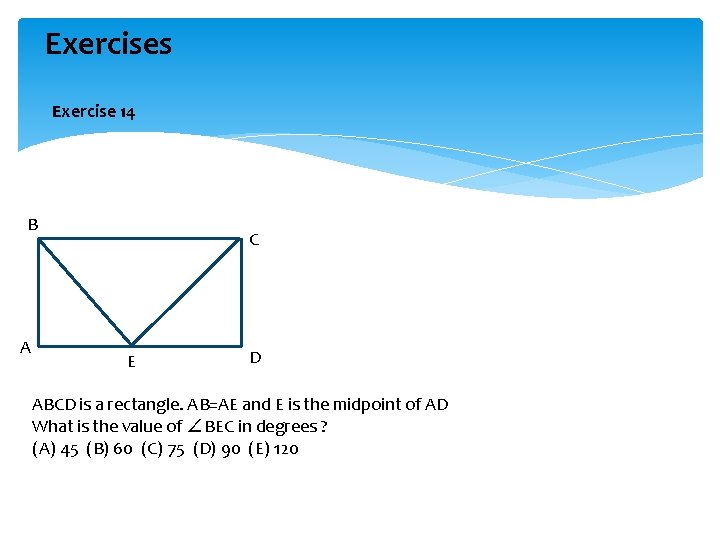
Exercises Exercise 14 B A C E D ABCD is a rectangle. AB=AE and E is the midpoint of AD What is the value of ∠BEC in degrees ? (A) 45 (B) 60 (C) 75 (D) 90 (E) 120

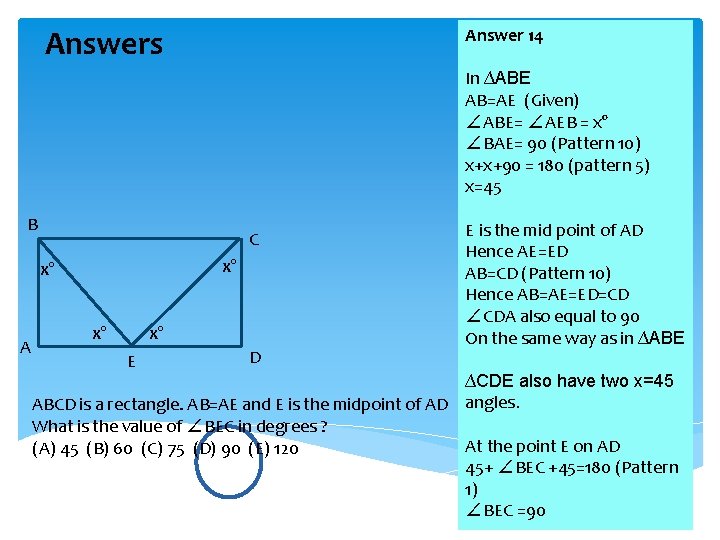
Answers Answer 14 In ∆ABE AB=AE (Given) ∠ABE= ∠AEB = x° ∠BAE= 90 (Pattern 10) x+x+90 = 180 (pattern 5) x=45 B C x° x° A x° x° E D E is the mid point of AD Hence AE=ED AB=CD (Pattern 10) Hence AB=AE=ED=CD ∠CDA also equal to 90 On the same way as in ∆ABE ∆CDE also have two x=45 ABCD is a rectangle. AB=AE and E is the midpoint of AD angles. What is the value of ∠BEC in degrees ? At the point E on AD (A) 45 (B) 60 (C) 75 (D) 90 (E) 120 45+ ∠BEC +45=180 (Pattern 1) ∠BEC =90

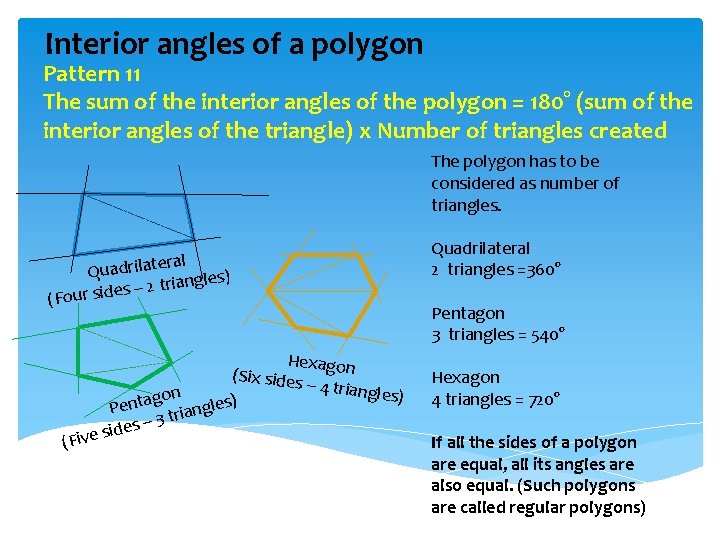
Interior angles of a polygon Pattern 11 The sum of the interior angles of the polygon = 180° (sum of the interior angles of the triangle) x Number of triangles created The polygon has to be considered as number of triangles. ral Quadrilate gles) n ia r t 2 – s (Four side (F Hexagon (Six sides – 4 triang n les) o g a ) t s n e l e P iang r t 3 es – d i s e v i Quadrilateral 2 triangles =360° Pentagon 3 triangles = 540° Hexagon 4 triangles = 720° If all the sides of a polygon are equal, all its angles are also equal. (Such polygons are called regular polygons)

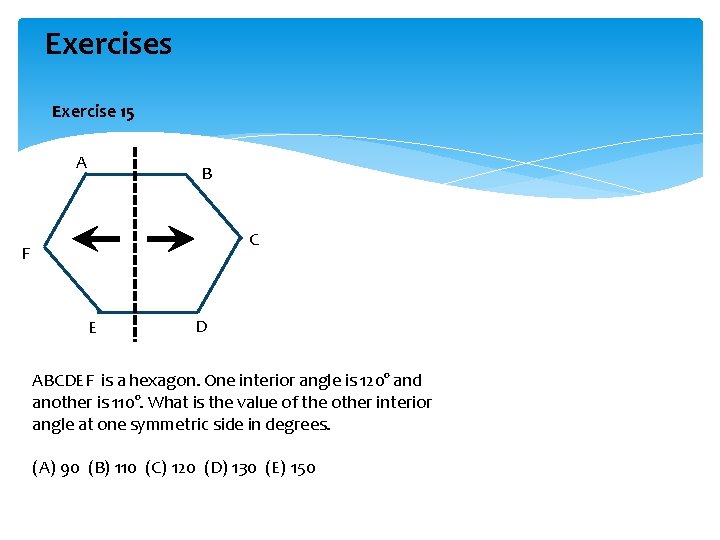
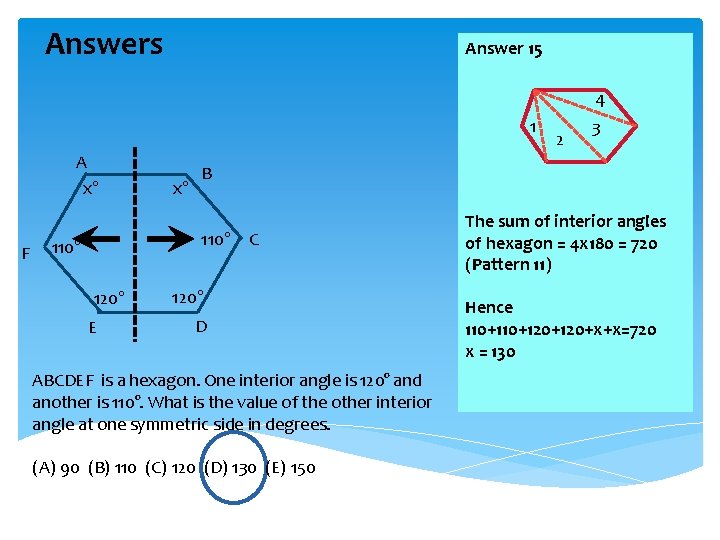
Exercises Exercise 15 A B C F E D ABCDEF is a hexagon. One interior angle is 120° and another is 110°. What is the value of the other interior angle at one symmetric side in degrees. (A) 90 (B) 110 (C) 120 (D) 130 (E) 150

Answers Answer 15 4 1 A x° F x° 120° E 3 B 110° C 110° 2 120° D ABCDEF is a hexagon. One interior angle is 120° and another is 110°. What is the value of the other interior angle at one symmetric side in degrees. (A) 90 (B) 110 (C) 120 (D) 130 (E) 150 The sum of interior angles of hexagon = 4 x 180 = 720 (Pattern 11) Hence 110+120+x+x=720 x = 130