Sannsynlighetsregning Normative modeller Rasjonelle vurderinger Deskriptive modeller Faktiske

Sannsynlighetsregning Normative modeller Rasjonelle vurderinger Deskriptive modeller Faktiske vurderinger

Sannsynlighetsregning i hverdagen • Når noe skal skje ”rettferdig” lar vi ofte ”tilfeldighetene råde” – Slå mynt og kron – LOTTO-trekning • Sannsynlighet og gunstige valg

Utfallsrom • En opplisting av hvilke utfall som er mulige • S = det totale utfallsrom • Mulige utfall kalles elementer • Eksempler: – Terningkast: S = {1, 2, 3, 4, 5, 6} – Kaste en mynt: S = {mynt, kron} – LOTTO-tall: S = {1, 2, 3, …, 32, 33, 34}

Generelt • Det totale utfallsrommet S består av m elementer • P(A) = sannsynligheten for at begivenhet A skal inntreffe • Begivenheten A består av k elementer • 0 P(A) 1 • P(S) = 1

Uniforme sannsynlighetsmodeller • Alle utfall har like stor sannsynlighet for å inntreffe • Symmetriske utfallsrom

Beregning av sannsynlighet ved symmetriske utfallsrom P(A) = k m P(A) = sannsynligheten for at hendelse A skal inntreffe k = antall elementer i hendelse A m = antall mulige utfall i S

Eksempel: terningkast • Utfallsom: S = {1, 2, 3, 4, 5, 6}, m = 6 • A = terningen viser like antall øyne • Like antall øyne: A = {2, 4, 6}, k = 3 k 3 1 P(A) = = 0. 5 m 6 2

Mengdelære • Union: A union B: alle elementer som er med i A, eller B, eller i begge S S • Snitt: A snitt B: alle elementer som samtidig er med i både A og B A A B x B

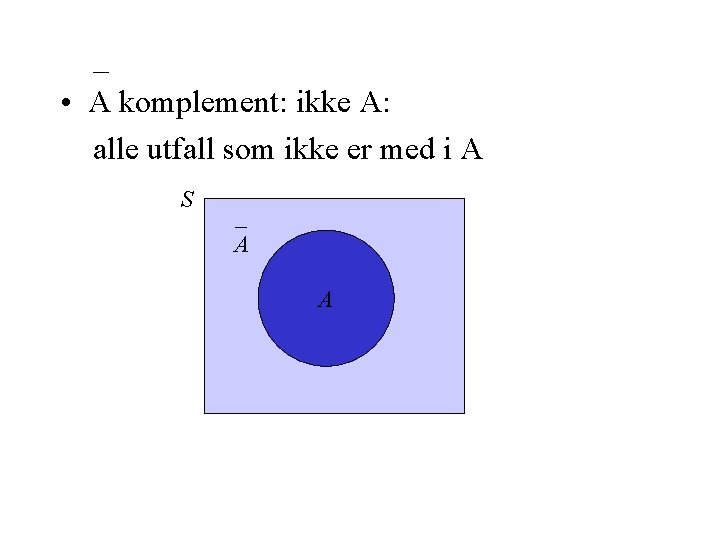
_ • A komplement: ikke A: alle utfall som ikke er med i A S _ A A

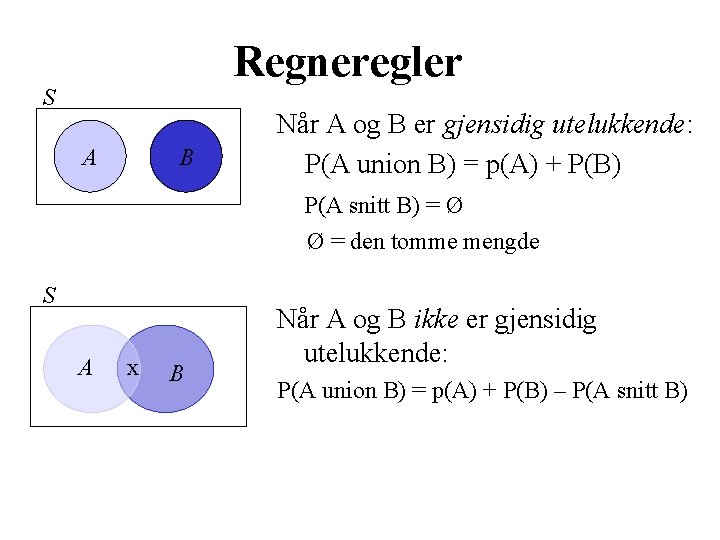
Regneregler S A B Når A og B er gjensidig utelukkende: P(A union B) = p(A) + P(B) P(A snitt B) = Ø Ø = den tomme mengde S A x B Når A og B ikke er gjensidig utelukkende: P(A union B) = p(A) + P(B) – P(A snitt B)

Forts. regneregler S _ A A _ P(A) = 1 – P(A) P(S) = 1 _ P(S) = P(A) + P(A) = 1 ___ => P(A) = 1 – P(A)

Sannsynlighet for samtidige eller påfølgende hendelser Generelt: P(A snitt B) = P(A) · P(B) Gjelder når A og B er statistisk uavhengige To hendelser er statistisk uavhengige hvis: P(A|B) = P(A) eller hvis P(B|A) = P(B)

”Tre-diagram” M. 50 Andre kast M. 50 Utfall MM . 50 K MK . 50 M. 50 KM K . 50 Første kast P(MM) = P(M) = 0. 25 K KK

Ordnede versus ikke-ordnede utvalg uten tilbakelegging • Ordnede utvalg: rekkefølgen av uttrekkingen av utvalget har en betydning – Eksempel: trekking av 1. og 2. premie • Ikke-ordnede utvalg: rekkefølgen av uttrekningen har ikke betydning – Eksempel: trekking av LOTTO-tall

Trekking med og uten tilbakelegging Med tilbakelegg. R RR R B RB S RS R BR B B BB S BS R SR S B SB S SS Uten tilbakelegg. B RB R = rød kule B = blå kule R S = sort kule S RS R BR B S BS R SR S B SB

Regneregler for antall kombinasjonsmuligheter ved trekking uten tilbakelegging • Antall ordnede utvalg: (n)r = n(n – 1)…(n – r + 1) (1) • Antall ikke-ordnede utvalg: n (n)r n(n – 1)…(n – r + 1) ( )= = (2) r r! r(r – 1) … 2 · 1 n = antall objekter, r = antall trekkinger

Eksempel: Valg av styre: antall mulige styrer versus antall styresammensetninger Tre kandidater: Tor, Odin og Loke Antall styrer (ikke-ordnet) Tor - Odin Tor - Loke Odin - Loke Antall styre sammensetninger (ordnet: leder-sekretær) Tor - Odin - Tor - Loke - Tor Odin - Loke - Odin

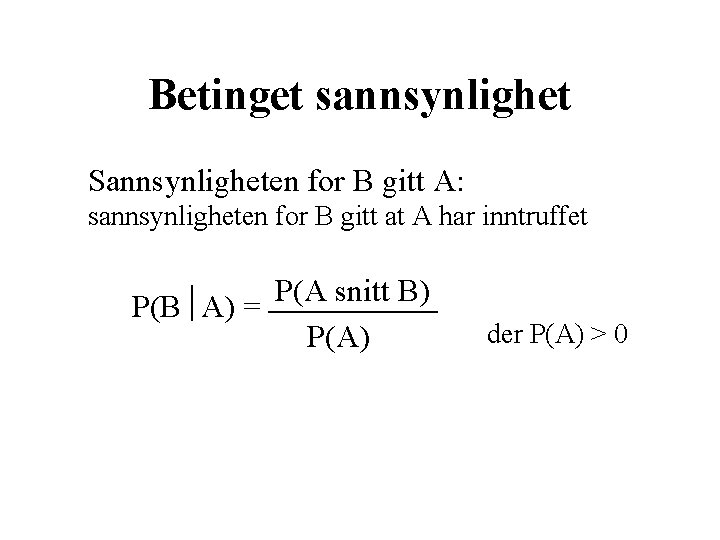
Betinget sannsynlighet Sannsynligheten for B gitt A: sannsynligheten for B gitt at A har inntruffet P(A snitt B) P(B A) = P(A) der P(A) > 0

Eksempel: betinget sannsynlighet Heltid Deltid Sum K 80 40 120 M 60 20 80 Sum 140 60 200 A: heltidsstudent B: kvinne P(A snitt B) P(B|A) = = P(A) 80 = 0. 57 140