Sampling Theorem frequency resolution Aliasing The Sampling Theorem

Sampling Theorem, frequency resolution & Aliasing The Sampling Theorem will be the single most important constraint you'll learn in computer-aided instrumentation design Consider a periodic function, with period T:

Fourier Series Where we have applied a low-pass “anti-aliasing” filter to the raw analog signal ending up with h(t), a signal with a highest freq component < 10*ω0

Ak , Bk: Fourier spectrum coefficients Or…generate 20 independent equations by sampling. We must sample 20 times during one period. (If we sample over more than one period, we may not end up with independent equations. ) Each equation will be of the form: {tm} is the set of sample times…

The matrix (C) of coefficients looks like:

Let the 20 x 20 matrix be C: with the solution Where matrix C must have a non-zero determinant

Coefficients become spectrum: magnitude Phase change as a function of ω:

Spacing of samples If the sample spacing is uniform there will be 2 N segments of time, (time between samples) Therefore the sample rate is 2 N/T. The maximum frequency in h(t) is Therefore you must sample at at least 2*fmax to insure you can resolve fmax freq.

statement of the Sampling Theorem, from A. V. Oppenheim and A. S. Willsky, Signals and Systems, 2 nd Ed. Prentice-Hall (1996) p. 518

Nyquist what? • Terminology: The sampling frequency of a particular situation, which may exceed by quite a bit the maximum frequency in the signal, is the Nyquist frequency. Twice the maximum frequency of the signal is called the Nyquist rate, and is the minimum sampling rate that can resolve the signal. (O&W, 1 st Ed, p. 519)

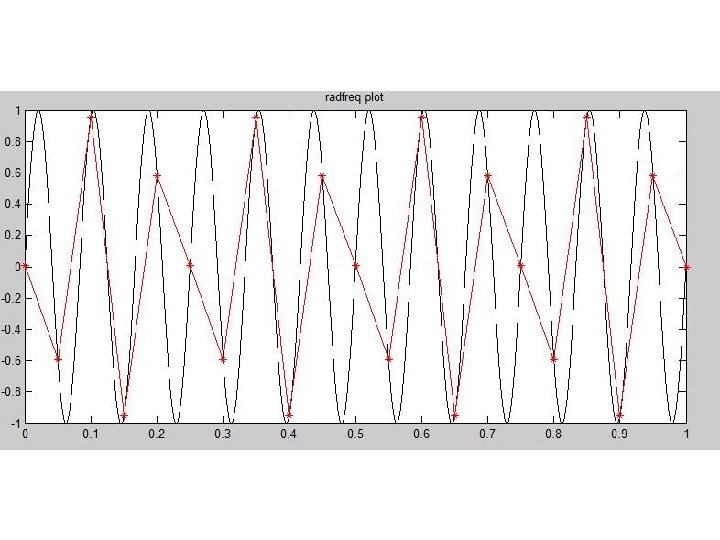
Resolvable frequency in spectrum • Given the sampling rate, and the number of samples taken, what is the Δf between points on the spectrum? • If a waveform is sampled for one second, what is the frequency resolution? • No matter how long you sample for, the maximum reconstructable frequency remains 2*f_samp

function Test_FFT_11 c(wind_flg)

Discrete Fourier Transform • Transform vs Series? • Computing the coefficients can take time…(bench) • Demo with Matlab fft and ifft functions (& Lab 6 HP ‘scope) • And the inverse Discrete Fourier Transform…

Power spectrum • A faster algorithm, the Fast Fourier Transform (FFT), is normally computed, for example, in Lab. VIEW or MATLAB or in the math feature of the HP 54622 A digital scope. • Power spectrum: The HH(jw) are usually complex numbers, and their magnitudes must be taken to find the Power Spectrum (in Matlab, abs(HH))

FFT solves a slightly different problem… • If resolution is ∆f then the FFT stops at Fsamp/2 - ∆f which makes sense, since what exactly happens at Fsamp/2 itself? • Convert FFT results to Fourier Series coeff: An = real( FFT(n+1) ) * (2/Nsamp) Bn = -imag( FFT(n+1) ) * (2/Nsamp)

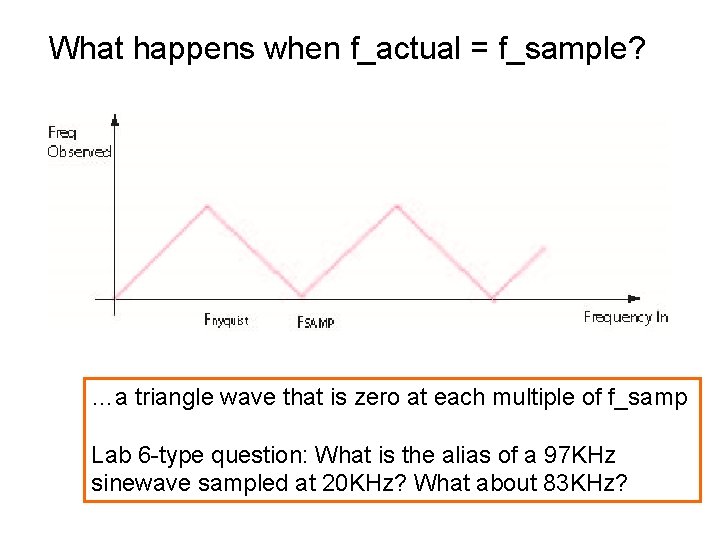
Aliased frequencies • Frequencies above the half the sampling rate become aliased as lower frequencies. • For frequencies just above half the sampling rate, up to the sampling rate, the aliased frequency falias = fnyq-|factual - fnyq|, a kind of mirror-image result. • Matlab example (workjddalias 03. m) • 12 Hz sinewave requires greater than 24 Hz sampling rate to preserve correct frequency in reconstruction. • Result of sampling 12 Hz at 20 Hz: alias freq = 10 - abs(12 -10) = 8 Hz.

What happens when f_actual = f_sample? …a triangle wave that is zero at each multiple of f_samp Lab 6 -type question: What is the alias of a 97 KHz sinewave sampled at 20 KHz? What about 83 KHz?

Another try at a formula for aliased frequency where fsamp = 40 and fact = 108 Fsamp = 40 Fact = 108 frac = rem(Fact, Fsamp) BB = floor(frac/( Fsamp/2) ) fobs = frac + BB * (Fsamp - 2*frac)

Strobe light demo • For Mech Engineers, goal is to find “zero frequency” and discover angular speed of rotating machinery. tedkinsman. photoshelter. com

About the strobe: General Radio 1531 A, from 1971. The circuit used to drive the 10 microseconds ON of the Xenon flash tube is similar to a defibrillator: Charging a capacitor up to several hundred volts. Why no new strobe models on the market? Fear of lawsuits about epilepsy, or the high voltage?

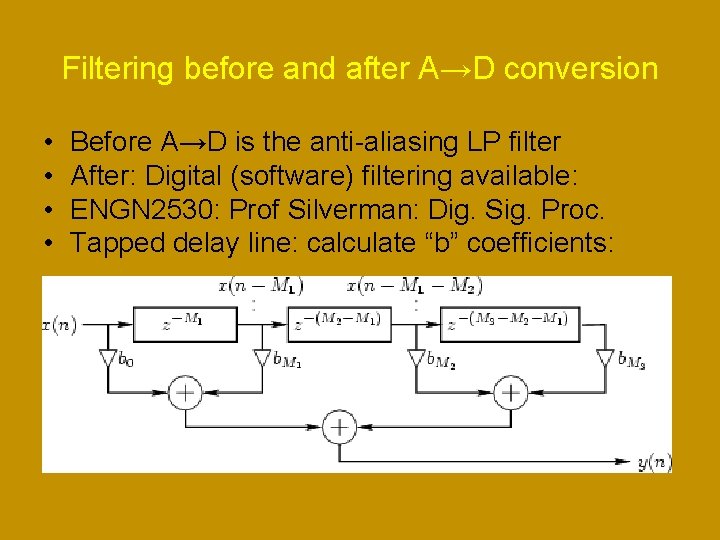
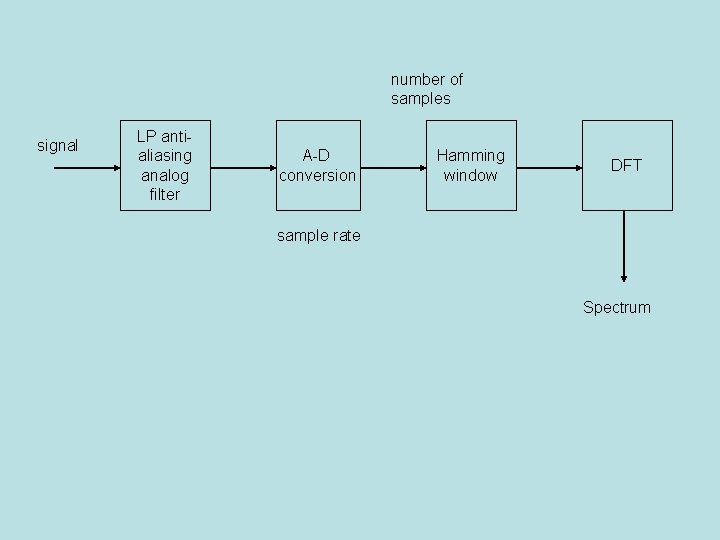
Filtering before and after A→D conversion • • Before A→D is the anti-aliasing LP filter After: Digital (software) filtering available: ENGN 2530: Prof Silverman: Dig. Sig. Proc. Tapped delay line: calculate “b” coefficients:

Windows to <weight> a sample of points (or filter coefficients) • A window is vector that weights point-for-point (dot product) part of a sequence of data; outside the window the sequence is set to zero. • Rectangular window • Cosine, Hann, Hamming windows • For dealing with time-sample sequence that doesn’t start and end at the same value • http: //en. wikipedia. org/wiki/Window_function#Cosine_window

number of samples signal LP antialiasing analog filter A-D conversion Hamming window DFT sample rate Spectrum