SAMPLING METHODS In statistical inference a sample is

SAMPLING METHODS

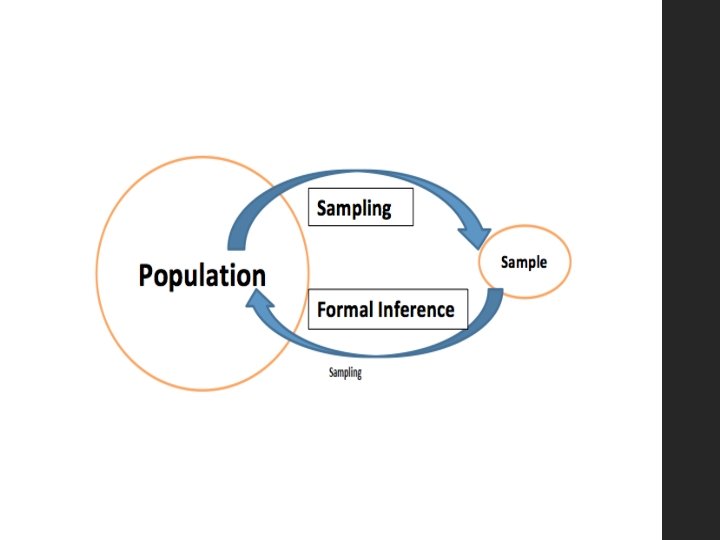
• In statistical inference, a sample is taken from the population, analysed in every which way possible, and used to make an inference about the population. • One of the key factors in this process working, is that the sample selected be representative of the population from which it is taken so that inferences about the population are the best that they can be.

The means used to obtain a sample is called a sampling method. Sampling methods can be categorized as Probability based and Non-probability based methods

Probability Sampling Methods • Simple Random Sampling • Stratified Random Sampling • Systematic Sampling • Cluster Sampling

RANDOM SAMPLING METHODS • Random sampling techniques are used in order to select a representative sample. • A representative sample is one which has similar enough characteristics to the population

Non-probability Sampling (aka The Dark-Side) • Convenience Sampling • Consecutive Sampling/Sequential sampling • Judgmental/Purposive Sampling

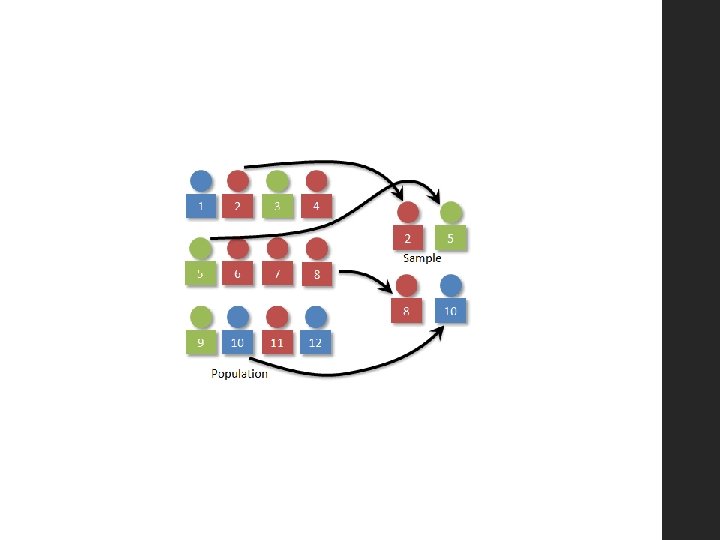
SIMPLE RANDOM SAMPLING • Each member of the population is assigned a number from 1 through to the total number in the population. • Random numbers are then generated and we select those members for the sample (if a number repeats it is ignored). • Eg. Lets say we’re picking from a population of 200. • First, you’ll give them all members a number from 1– 200. • Then the computer will churn out a random number. For example, it could churn out a 3 • add data from member number 3 to the sample • Then the computer churns out another random number. If it churns out 3, ignore it and try again. If it churns out 182, add data from member number 182. • Keep doing this till you get the desired number of members in your sample.

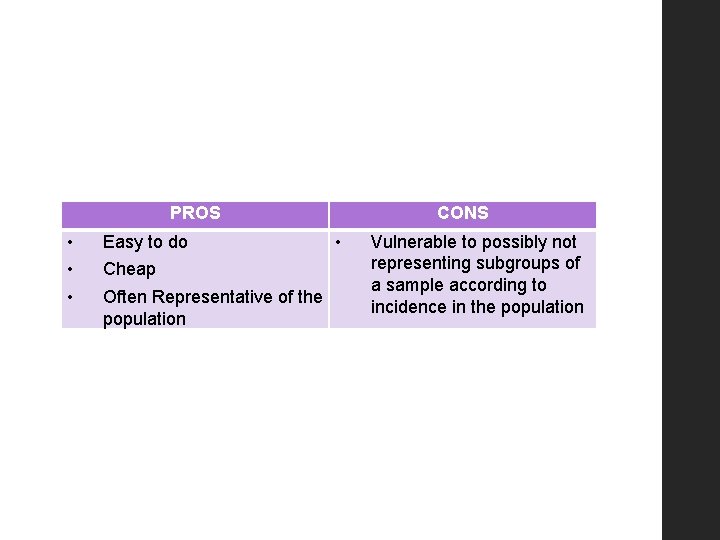
PROS • • • Easy to do Cheap Often Representative of the population CONS • Vulnerable to possibly not representing subgroups of a sample according to incidence in the population

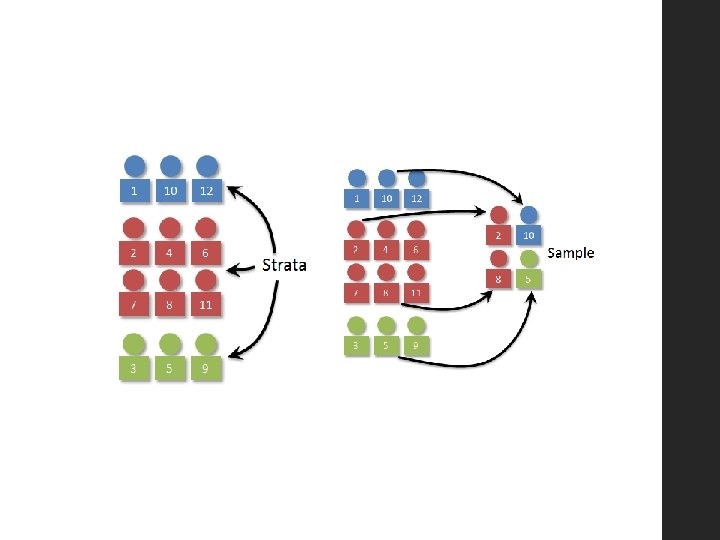
STRATIFIED RANDOM SAMPLING • This method divides the population into strata (subgroups which have no overlap). These strata are then represented proportionally in the sample. • E. g. In the largest fast food franchise in the country, Cheddar Cheese Tonight, 80% of the workers are female and 20% are male. The CEO “wonders if the median sick days of employees older than 50 tends to be higher than the median sick days of employees younger than 50 across all Cheddar Cheese Tonight’s in New Zealand? ” • In this case, stratified sampling could be better than simple random sampling. You could stratify by gender to make sure there is a proportional number of males and females in both groups (older than 50 employees group AND younger than 50 employees group) Method: • Your data should be split into an “older than 50 employees” group AND a “younger than 50 employees” group • Further split each group into a men’s section a women’s section. • To find number of women in each sample • To find number of men in sample = 80% of 30 = 24 = 20% of 30 = 6 • Using simple random sampling, 24 women would be selected from the “older than 50” group. Then, using simple random sampling 6 men would be selected from the “older than 50 group” • The same process would be applied to the younger than 50 group

Stratified sampling makes sure subgroups in the population are the same in the sample as they are in the population. I. e. That if the population has 80% females the sample will have 80% females SIMPLE RANDOM SAMPLING SHOULD DO THIS ANYWAY! But on some instances we need to be doubly sure, and in these cases stratified sampling is used.

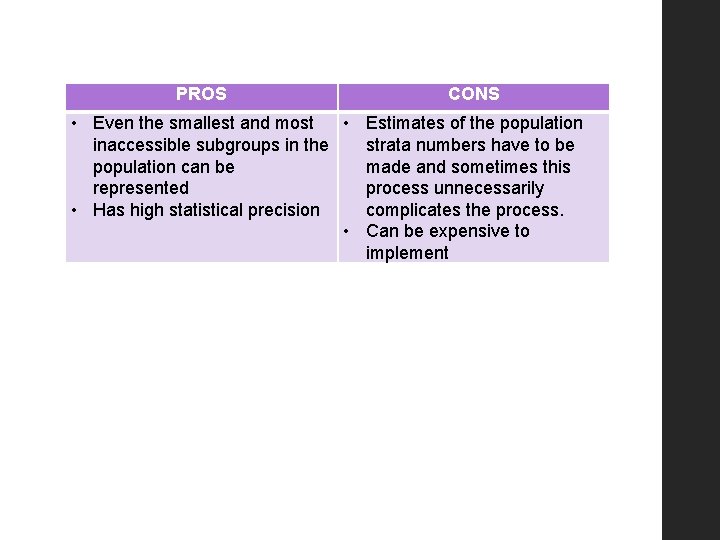
PROS CONS • Even the smallest and most • Estimates of the population inaccessible subgroups in the strata numbers have to be population can be made and sometimes this represented process unnecessarily • Has high statistical precision complicates the process. • Can be expensive to implement

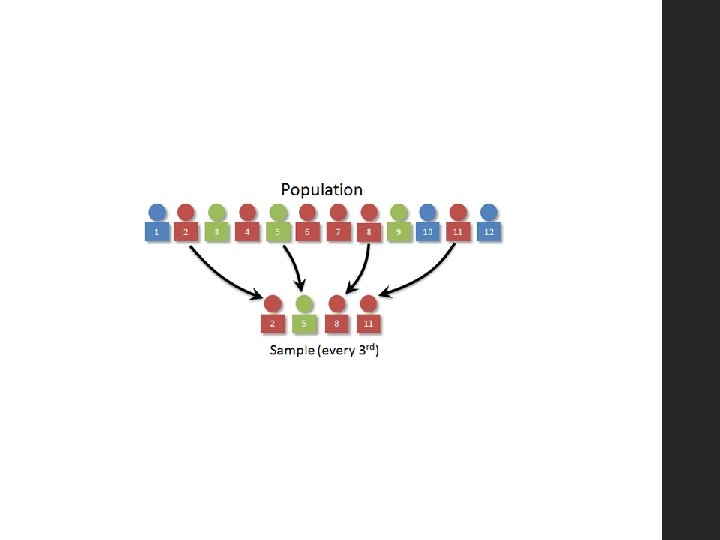
RANDOM SAMPLING METHODS • Systematic Sampling: Members are chosen at regular intervals on a list, using a calculated step size, and beginning at a randomly chosen starting point within the first ‘step’. • E. g. To choose a sample of 30 from a sample of 500, start by determining the step size: • Step Size = 500 divided by 30 = 17 (to the nearest whole number) • Then, churn out a random number to work out the ‘starting point’ between 1 and 17 (For example, 10) • So start with member 10, and then add every 17 th member from then on. • Or member 10, 27, 44, 61, …

PROS • • Easy to do Each member of the population has an equal chance of being selected. CONS • Not representative if the population has periodicity (a pattern) in it that is the same as the sample pattern (n’th data item)

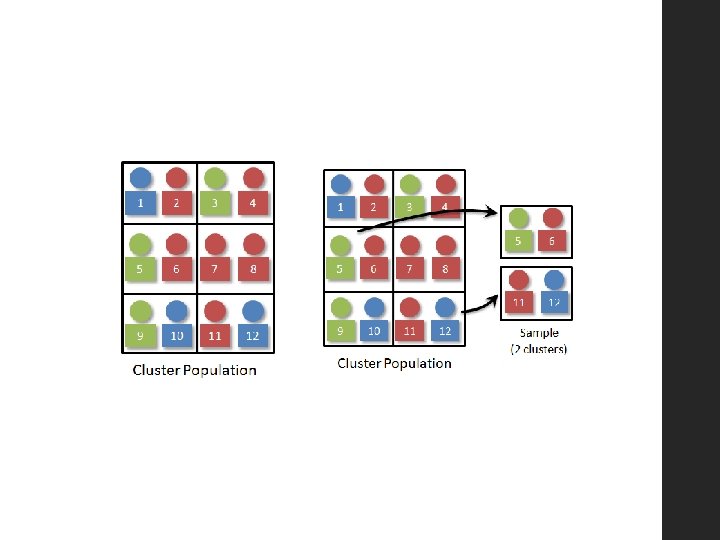
CLUSTER SAMPLING • It may be possible to split a large population into smaller groups called clusters, with each cluster having the same characteristics as the entire population. One (or more) of these clusters can be chosen at random, then a sample is drawn from this cluster using the earlier techniques. • Eg. A Waikato company’s best seller is their Sweetas. Chedder cereal. They are administering a survey around the taste rating of their product. They “wonder if the median score of people with children in rural Waikato tends to be greater than the median score of people without children in rural Waikato? ” • The survey involves a survey administrator approaching the person, having a bowl of cereal, and going through some questions they might not understand or respond correctly to without the administrator being present. • If we use simple random sampling (randomly choose people you know are from rural Waikato), our poor administrator will have to meet people all over the central North Island. • Quite expensive and very inconvenient

CLUSTER SAMPLING • Rather, we could choose from clusters (small groups that we feel will be representative of the population) • Eg. We could pick 5 towns in Rural Waikato • (1)Te Kuiti (2)Otorohanga (4)Te Awamutu (5)Matamata • Randomly pick 2 of them (Ran # Generator churns out: 2, 5) • Simple random sample from the populations of Otorahonga and Matamata. • Now our administrator can administer the survey to all those randomly chosen from Otorohonga, and then drive to Matamata and administer the survey to all the sample points there. • Now that is far more convenient (and cheap!) (3)Tokoroa

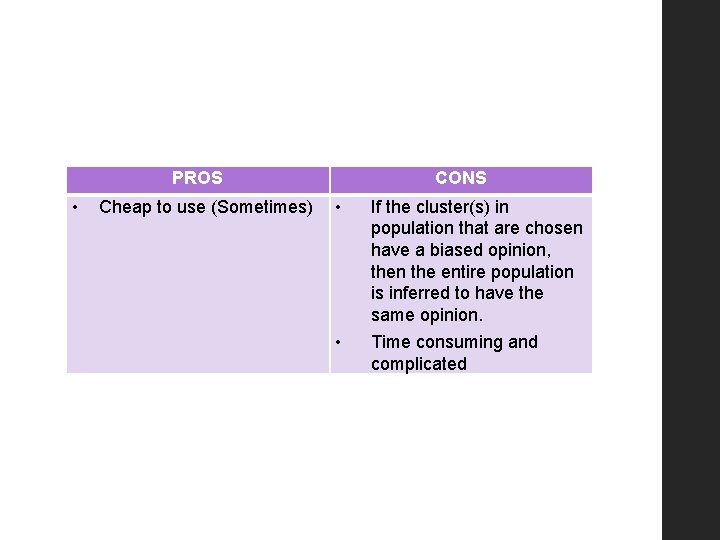
PROS • Cheap to use (Sometimes) CONS • If the cluster(s) in population that are chosen have a biased opinion, then the entire population is inferred to have the same opinion. • Time consuming and complicated

Non-Probability Sampling aka The Dark-Side • In any form of research, true random sampling is always difficult to achieve. • Since many researchers are bounded by time, money and workforce, the researcher sometime resorts to nonrandom methods of sampling I know son, what a sick twisted world we live in!

• Non-probability sampling is where the samples are gathered in a process that does not give all the individuals in the population a probability of being selected. • The sample may or may not represent the entire population accurately. Therefore, the results of the research cannot be used in generalizations about the entire population.

Convenience Sampling The samples are selected because • They are accessible to the researcher. • They are easy to recruit. They can be a self-selection of individuals willing to participate. (a self-selected sample) E. g. Like asking random people leaving a mall.

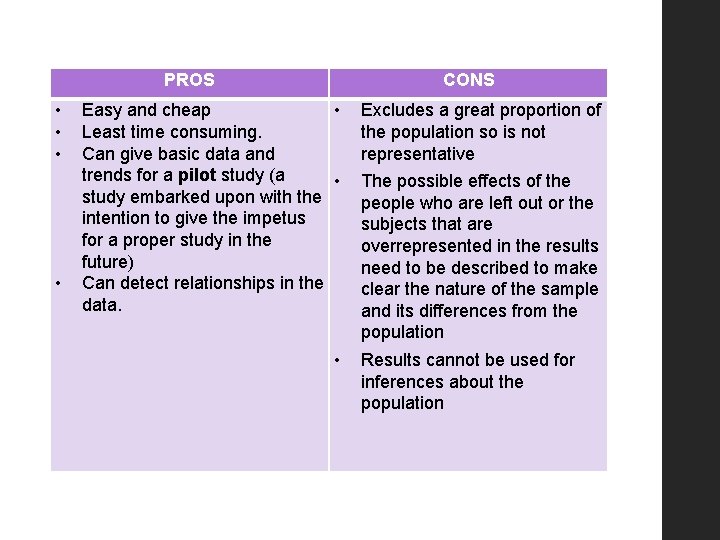
PROS • • CONS Easy and cheap • Least time consuming. Can give basic data and trends for a pilot study (a • study embarked upon with the intention to give the impetus for a proper study in the future) Can detect relationships in the data. • Excludes a great proportion of the population so is not representative The possible effects of the people who are left out or the subjects that are overrepresented in the results need to be described to make clear the nature of the sample and its differences from the population Results cannot be used for inferences about the population

Consecutive Sampling / Sequential Sampling • Consecutive sampling • Includes ALL accessible subjects, that are available, as part of the sample • The sampling schedule is completely dependent on the researcher • E. g. Accessing medical data records of all patients data I have access to (say 150 odd patients), rather than a sample of 150 which was decided at random from the population.

PROS CONS • Limitless options when it • Not representative of the comes to sample size and the population unless the sample timing of the sampling. is a very large fraction of the • Not expensive or time population consuming • Not random and cannot be • Does not require a large work used for inferences about the force population

Judgmental Sampling / Sampling Purposive • The researcher believes that some subjects are more suitable to be sampled for the research than others individuals. So they are purposively chosen as subjects. • It is usually used when a limited number of individuals possess the trait of interest. • It is the only viable sampling technique to obtain information from a very specific group of people. • Judgmental sampling can be used if the researcher knows a reliable professional or authority that he thinks is capable of assembling a representative sample.

• E. g. A TV researcher wants a quick sample of opinions about a political announcement. They stop what seems like a reasonable cross-section of people in the street to get their views. • E. g. In a study where a researcher wants to know what teaching methods help a student obtain Excellence in NZQA Level 3 Statistics, the only people who can give the researcher first hand advice are those students who are generally capable of getting excellence in this subject. Perhaps the teacher would be asked to make that judgment as to who should take part in the study…

PROS • Easy, fast and convenient CONS • No way to assess the reliability of the “expert” who chose the sample • Results cannot be used to make inferences about the population.