Sampling Methods and the Central Limit Theorem Chapter











- Slides: 16

Sampling Methods and the Central Limit Theorem Chapter Eight Mc. Graw-Hill/Irwin © 2006 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Objective of inferential statistics is to determine characteristics of a population based on a sample Why sample? • The physical impossibility of checking all items in the population. • The cost of studying all the items in a population. • The time-consuming aspect of contacting the whole population. • The destructive nature of certain tests. • The adequacy of sample results in most cases.

Sampling Methods Simple Random Sample: A sample selected so that each item or person in the population has the same chance of being included. One can also a table of random numbers (Appendix E)

Systematic Random Sampling: Every kth member of the population is selected for the sample.

Stratified Random Sampling: A population is first divided into subgroups, called strata, and a sample is selected from each stratum. Eg. College students may be stratified into freshmen, sophomore, etc. or simply male and female

Cluster Sampling: A population is first divided into primary units then samples are selected from the primary units.

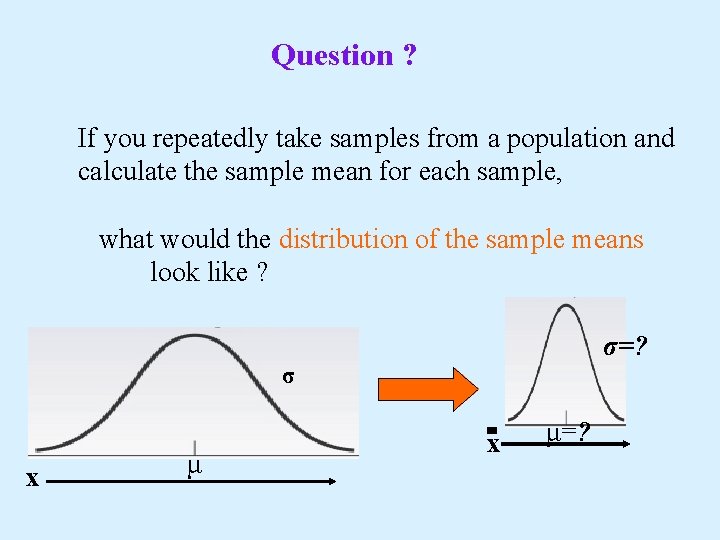
Question ? If you repeatedly take samples from a population and calculate the sample mean for each sample, what would the distribution of the sample means look like ? σ=? σ x μ=?

Demo the CLT using Visual Statistics software

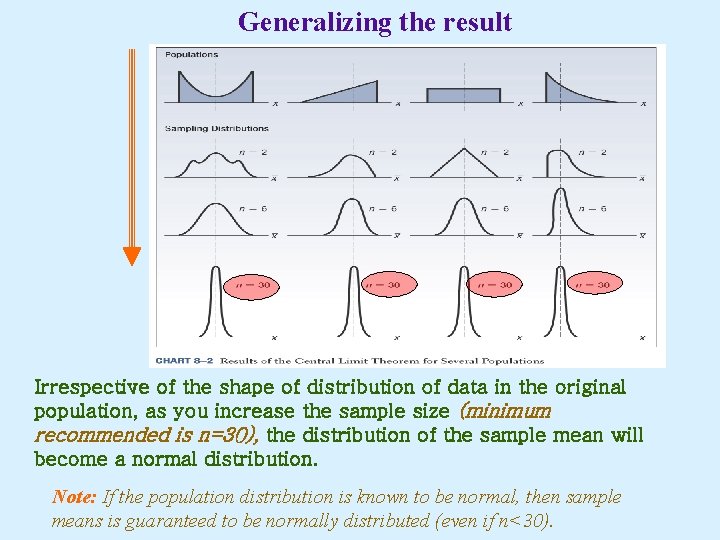
Generalizing the result Irrespective of the shape of distribution of data in the original population, as you increase the sample size (minimum recommended is n=30), the distribution of the sample mean will become a normal distribution. Note: If the population distribution is known to be normal, then sample means is guaranteed to be normally distributed (even if n<30).

Central Limit Theorem If all samples of a particular size are selected from any population, the distribution of the sample mean is approximately a normal distribution.

As n increases μx will approach μ. So sample mean is a good estimator of population mean. This s. d. is called the standard error (ie. , of the mean distribution). sx = s n Note that the Std Error is smaller

Variance of the sample mean distribution x 1 is mean of Var(x) = Var (x 1 + x 2 +…+xn) Where sample 1, x 2 is …) n = 1 [Var(x 1) + Var(x 2) + … +Var(xn)] n 2 = 1 [σ2 + … + σ2] = 1 [n. σ2] = n 2 σx 2 = σ2 n therefore, Standard Deviation = σ/√n (Remember this formula!) n σ2 n 2

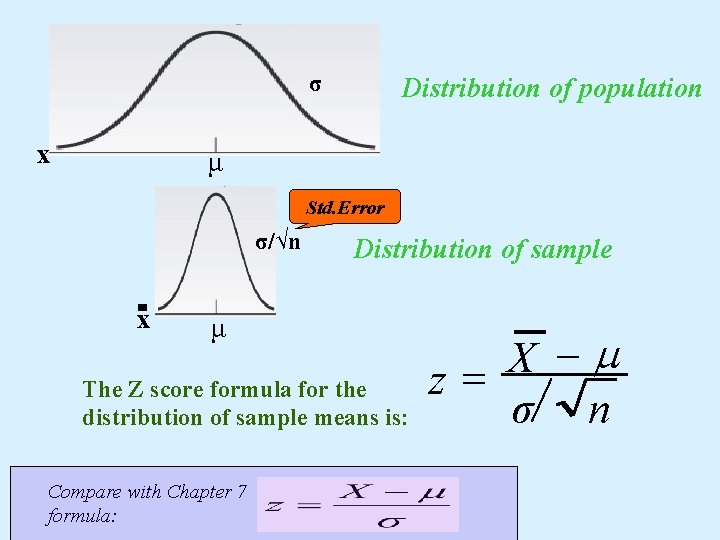
σ x Distribution of population μ Std. Error σ/√n x Distribution of sample μ The Z score formula for the distribution of sample means is: Compare with Chapter 7 formula: -m X z= σ n

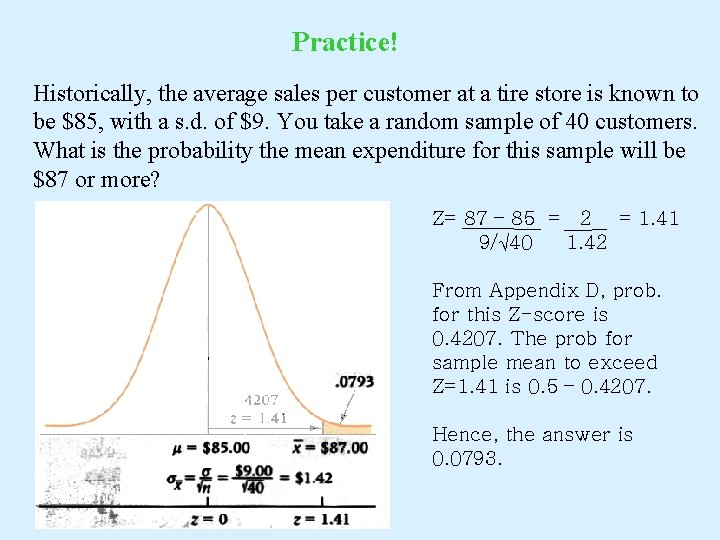
Practice! Historically, the average sales per customer at a tire store is known to be $85, with a s. d. of $9. You take a random sample of 40 customers. What is the probability the mean expenditure for this sample will be $87 or more? Z= 87 – 85 = 2 = 1. 41 9/√ 40 1. 42 From Appendix D, prob. for this Z-score is 0. 4207. The prob for sample mean to exceed Z=1. 41 is 0. 5 – 0. 4207. Hence, the answer is 0. 0793.

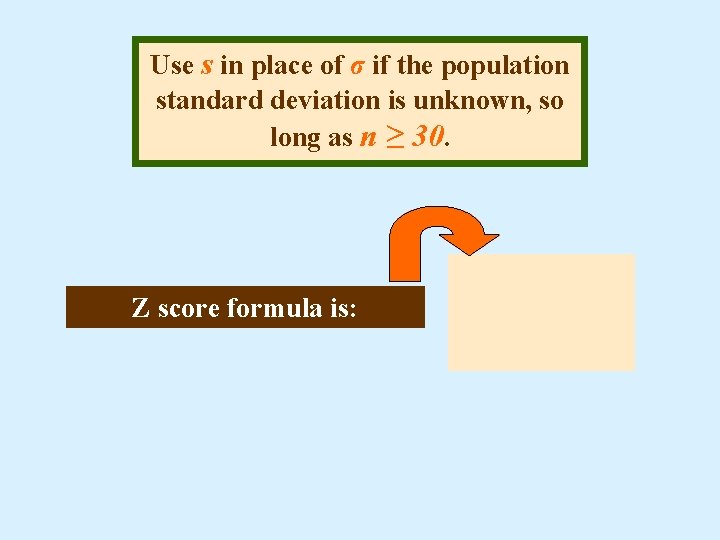
Use s in place of σ if the population standard deviation is unknown, so long as n ≥ 30. Z score formula is:

Practice time! Problem #17 on page 237 Z = 1950 -2200 = -7. 07 250/√ 50 So probability is virtually 1