SAMPLING ISSUES POPULATIONS AND SAMPLES Populations and Parameters

SAMPLING ISSUES

POPULATIONS AND SAMPLES Populations and Parameters – a Population is the entire collection of all observations of interest (people, objects, or events) as defined by the researcher – A parameter is a descriptive measure of the entire population of all observations of interest to the researcher. E. g. mean of a population variable

SAMPLES and STATISTICS Since it is not usually possible or practical to measure every individual person or event (a census) we take, • A Sample as a representative portion of the population which is selected for study • A Statistic is a characteristic of the sample used to estimate the equivalent population parameter

GENERALIZING FROM SAMPLE TO POPULATION Logically, the greater the similarity between our small sample and the large population (the more “representative” the sample is of the population) the better the sample statistic should estimate the population parameter

INFERENTIAL STATISTICS Inferential Statistics are used to provide the probability that a pattern found in your sample data will actually be true for your population. The term ‘inferential’ comes from the word ‘infer’. That is, from the results of our sample, what is the probability that we can infer the same sort of result for the larger population?

SURVEY VERSUS CENSUS • SURVEY: Systematic process of gathering information from a sample in order to study a population • CENSUS: A survey in which all of the population elements are included

CONCEPT OF SAMPLING • The concept of sampling therefore involves: – taking elements of the defined population according to acceptable procedures to ensure a representative sample – making observations/assessments on this smaller group of elements, then – generalizing findings back to the defined population from which the representative sample was drawn • Sampling Error – the difference between the unknown population parameter and the sample statistic being used to estimate the parameter.

SAMPLING ERROR There at least two possible causes of sampling error: 1. Sampling error is mere chance in the sampling process. 2. Sampling bias occurs when there is some tendency in the sampling process to select certain sample elements over others. For example, the sampling process may favour the selection of males to the exclusion of females, married persons to the exclusion of singles, or older employees rather than younger ones.

SAMPLING DISTRIBUTION • This is a distribution of all possible values of a statistic, e. g. means of all samples of the same size selected from a population is the sampling distribution of sample means. • The mean of the sampling distribution of all the means of all samples of the same size (n= 30+) from the population approximates to the population mean • The standard deviation of a sampling distribution is termed the standard error of the distribution of sampling means.

VARIABILITY OF SAMPLE MEANS • A random sample is never the same as the population because it does not contain the whole population and each sample of the same size contains data from a different set of individuals. • Therefore a range of sample means has variability (sampling distribution). • We can calculate the variability with a standard deviation to provide a numerical index of that variability just as we did with individual scores

STANDARD ERROR OF THE MEAN • The Standard Error of the Mean (SEm) the standard deviation of the distribution of sample means around the population mean • That is the SEm measures the variability of the sample means around the population mean.

CENTRAL LIMIT THEOREM Central Limit Theorem applies to theoretical situations where many different samples of the same size (N) are selected from a single population. It states: As sample size (number of observations in each sample) increases, there is a tendency for the sampling distribution of sample means to approximate to a normal distribution. With sample sizes of 30+ we can safely assume that the sampling distribution of means will approximate to a normal distribution.

STANDARD ERROR OF THE MEAN • The formula for the standard error of the mean (SEm) is: SEm = sample standard deviation sample size n • The SEm is much smaller than the SD of raw scores because sampling means are not as spread out as the original scores being derived from means of sets of raw scores. The equation makes it clear that as n (or sample size) increases so sampling error is reduced. SPSS calculates SEm as part of the descriptive statistics menu.

STANDARD ERROR OF THE MEAN • SEM is a very important statistic because it specifies precisely how well a sample mean estimates the population mean. • In most situations, we possess only one sample mean as an estimate of the unknown population mean. • Although we don’t expect the sample mean to be exactly the same as the population mean, the standard error of the mean will tell us how good an estimate it will be.

STANDARD ERROR OF THE MEAN • A small SEm implies that the sample mean is a close approximation to the population mean, while a larger one indicates that the sample mean is less efficient as an estimate of the population mean. • The larger the size of the sample, the more probable that the sample mean will be close (a good estimate of) to the population mean for the obvious reason that as sample size increases it becomes more like the population as there is more of the population in the sample

DISTRIBUTION OF SAMPLE MEANS • The material covered in earlier chapters helps us predict the probability of an individual score lying within a specified range of a normal distribution using the Z distribution. • This basic idea extends to standard error and sample means. • Therefore the Z distribution, percentages and probabilities that we used with individual values can be applied in exactly the same way with the normal distribution of sample means

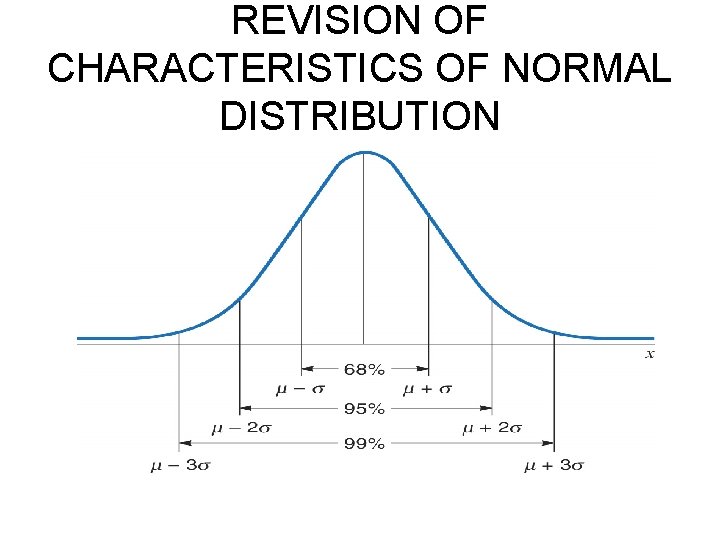
REVISION OF CHARACTERISTICS OF NORMAL DISTRIBUTION

% OF SAMPLE MEANS IN DIFFERENT PARTS OF A SAMPLE MEAN DISTRIBUTION • As the distribution of sample means is a normal distribution, the same proportions and probabilities met before with the normal distribution apply. • 68% of means of all same sized samples lie between + 1. 00 and – 1. 00 SEm (p = 0. 68) • 95% of means of all same sized samples lie between + 1. 96 and – 1. 96 SEm (p = 0. 95) • 99% of means of all same sized samples lie between + 2. 58 and - 2. 58 SEm (p = 0. 99) • These ranges are confidence intervals which indicate the probability the actual population mean lies within a given range around the sample mean.

PROBABILITIES • Restating the probabilities listed earlier, we can say that there is roughly a two in three chance (68%) that the difference (deviation) between the mean of the only obtained sample we possess and the true mean of the whole population will not exceed a value of one standard error either side. • Similarly, we can argue that in 19 cases out of every 20 (or 95 in 100) that the population mean will not lie outside twice the standard error either side.

Importance of Sampling Error and Standard Error • Most statistical analyses are attempts to disentangle sampling error or chance variation from real differences or relationships between samples so that we know if any real differences or relationships exist. • Real differences/relationships are ones that exceed those expected from random sampling differences alone. This is why we apply significance levels to the testing of hypotheses.

Importance of Sampling Error and Standard Error • A sample mean that is at or beyond 2 standard errors from the mean has a 5% or less likelihood of occurring by chance and therefore probably indicates a sample that is significantly different from the population i. e. possibly not part of that population.

STANDARD ERROR OF A PROPORTION • The standard error of a proportion (SEp) is obtained by means of the formula: SEp = pq n • where p represents the proportion of the sample possessing the characteristic in question, q represents the proportion that does not possess that characteristic, and n is the sample size.

HOW TO SAMPLE • Six Steps: – Define the population – Identify the sampling frame – Select a sampling technique – Determine the sample size – Select the sample elements – Collect the data from the designated elements

Sampling Step 1 • Define the population or collection of elements about which you wish to make an inference – For example: part-time employees, investment types, households, business firms, credit-card transactions – Define by geographic boundary, time period, and any other restrictions on elements • Higher incidence of elements qualifying for the sample will generally make data collection easier

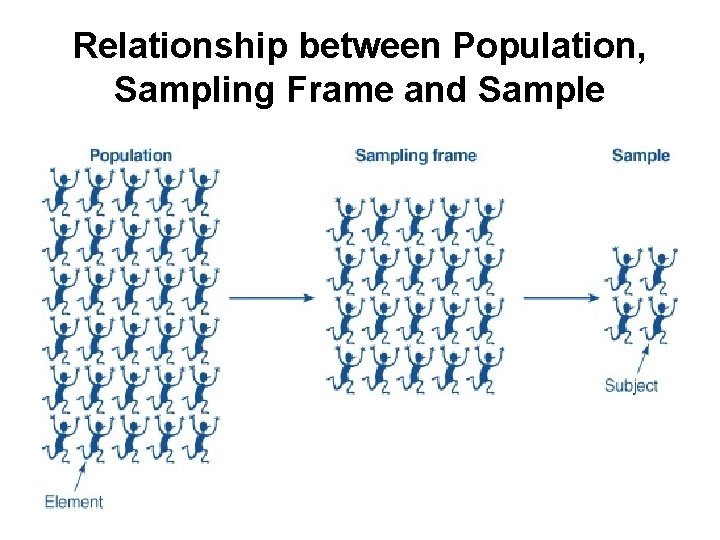
Sampling Step 2. Sampling Frames In most research, we are interested in what is ‘true’ for a very large number of people or organizations, our population of choice. We need a list of the population chosen so that we can select a sample. This list is the sampling frame. Common sampling frames are: Telephone or yellow page listing Electoral role Employee list Mailing list for professional organization, etc

Relationship between Population, Sampling Frame and Sample

Sampling Step 3: Selecting a Sampling Technique • Probability Sampling – all elements in the population have an equal chance or probability of being selected as sample subjects. Mainly used in Quantitative studies • Non-probability Sampling –the elements do not have a known or predetermined chance of being selected as subjects (often used in Qualitative studies) – There is no way of ensuring the sample is representative of the population – Often relies on the researcher’s judgement

Types of Probability and Non. Probability Sampling Non-Probability Opportunity Judgemental Quota Purposive Snowball Probability Simple random Systematic Stratified Cluster

Representative Sample Any part of a defined population which is selected on a probability basis, and from which information can be obtained and statistical inferences or predictions made about the entire population

SIMPLE RANDOM SAMPLING Each element has a known and equal chance of being selected Every sample of size n is a sample possibility, and is just as likely to occur as any other sample of size n Simple random samples can be drawn by use of computer generated random numbers or random number table Is the most representative of the population for most purposes

DISADVANTAGES OF SIMPLE RANDOM SAMPLING Disadvantages are: – Most cumbersome and tedious – The entire listing of elements in population is essential but frequently unavailable – Very expensive – Not the most efficient design

STRATIFIED SAMPLING • The parent population is divided into mutually exclusive and exhaustive subsets – strata or subpopulations, e. g. gender, age groups, salary groups. • Strata are usually easily discernible, and the proportion in each is predetermined, usually based on the proportions in the population although disproportional sampling is used should there be few units in one or more strata • A simple random sample is drawn from each subset

SYSTEMATIC SAMPLING • In systematic sampling, a serially numbered sampling frame (list of units) is necessary and every nth number is selected from a random starting point. • E. g. To take a 10 per cent sample one could select every tenth item/name/number from a complete list of names and/or addresses from the electoral roll or a firm's list of customers. • Systematic sampling can only be performed if the defined population can be listed serially in a sampling frame so that the sample can be drawn at fixed intervals from the list.

CLUSTER SAMPLING • Cluster sampling is the sampling of entire natural groups rather than individuals. • It is the clusters that are randomly sampled, e. g. all business faculties in the country’s universities are sampled to produce a sample of 6 faculties. Only students in those 6 faculties are surveyed. It can be thought of as a procedure in which the population is sampled in chunks or blocks, rather than as separate individuals. • It retains the principle of randomness yet allows a research design that is feasible in terms of cost, time and other resources.

MULTI-STAGE CLUSTER SAMPLING • There are often several stages or levels of random cluster sampling if large-scale organizations are being studied. • To sample employees of a national bank we would start by random sampling states to choose, say 6 states. • Next stage is to random sample for 5 branches in each state. • Next stage is to random sample 25% of the employees in each of the 30 branches previously selected.

NON-PROBABILITY SAMPLING • • • Opportunity or Convenience Sampling Judgemental Sampling Quota Sampling Purposive Sampling Snowball or Referral Sampling

CONVENIENCE (OPPORTUNITY) SAMPLING Convenience sampling involves data collection from elements that happen by chance to be available, e. g. local shopping centre; lecture theatre; phone-in poll of those listening to radio Empirical evidence suggests that even large convenience samples rarely prove to be representative Generally used in exploratory studies

JUDGEMENT SAMPLING • The sample elements are handpicked because it is expected they will serve the research purpose • Elements may be selected because it is judged they will be representative of the population of interest

Quota Sampling • The sample elements are selected in a way such that the proportion of elements possessing certain characteristics approximates the proportion in the population • Quotas for important characteristics may be missed • Bias can be introduced by judgement of the field worker collecting data • Difficult to verify if the sample is representative

PURPOSIVE SAMPLING Purposive sampling is explicitly chosen to be non-representative to achieve a specific analytical objective, for example, a survey of the country’s leading economists on the inflationary effects of petroleum costs on the forthcoming budget

SNOWBALL SAMPLING This method uses initial contacts to provide further contacts or cases through referrals. It is a bit like networking. Useful for small rather specialized populations where most members know of each other, e. g. interviews with international specialists on the potential development of geo-thermal energy.