Sampling Based Range Partition for Big Data Analytics

Sampling Based Range Partition for Big Data Analytics + Some Extras Milan Vojnović Microsoft Research Cambridge, United Kingdom Joint work with Charalampos Tsourakakis, Bozidar Radunovic, Zhenming Liu, Fei Xu, Jingren Zhou INQUEST Workshop, September 2012

Big Data Analytics • Our goal: innovation in the area of algorithms for large scale computations to move the frontier of the computer science of big data • Some figures of scale – – Peta / Tera bytes of online services data processed daily 200 M tweets per day (Twitter) 1 B of content pieces shared per day (Facebook) 8, 000 Exabytes of global data by 2015 (The Economist) 2

Research Agenda Database queries Machine learning Optimization Distributed computing system 3

Outline • Range Partition with Fei Xu and Jingren Zhou • Count Tracking with Zhenming Liu and Bozidar Radunovic • Graph Partitioning (def. only) with Charalampos Tsourakakis and Bozidar Radunovic 4

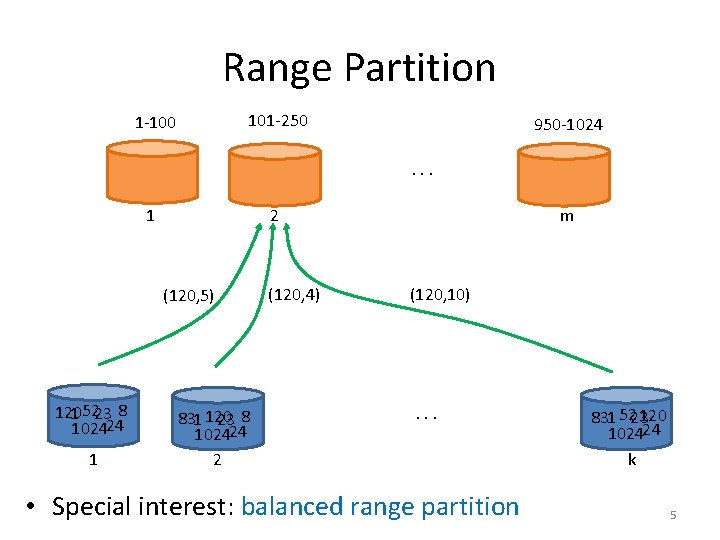
Range Partition 101 -250 1 -100 950 -1024. . . 1 2 (120, 5) 120 1 5223 8 102424 1 831 120 23 8 102424 2 (120, 4) m (120, 10) . . . • Special interest: balanced range partition 120 831 5223 102424 k 5

Range Partition Requirements • 6

Two Approaches • Sampling based methods – Take a sample of data items – Compute partition boundaries using the sample • Quantile summary methods – At each node compute a local quantile summary – Merge at the coordinator node 7

Related Work • 8

Related Work (cont’d) • 9

Problem • Range partition data while making one pass through data with minimal communication between the coordinator and sites 10

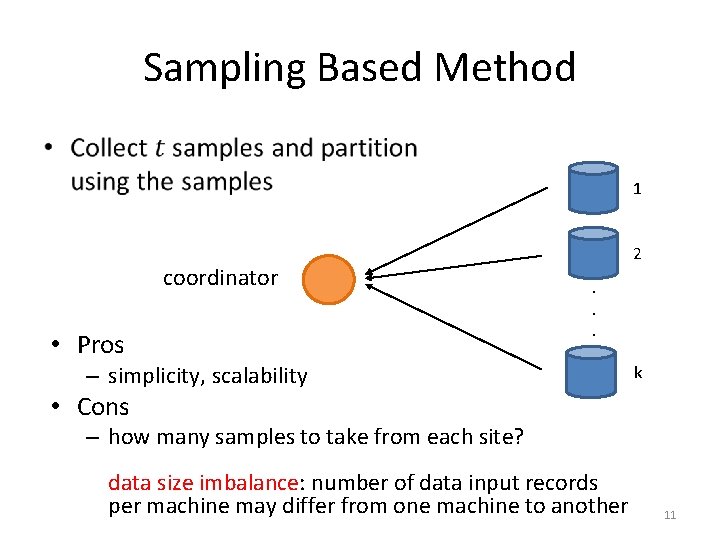
Sampling Based Method • 1 coordinator • Pros 2. . . – simplicity, scalability k • Cons – how many samples to take from each site? data size imbalance: number of data input records per machine may differ from one machine to another 11

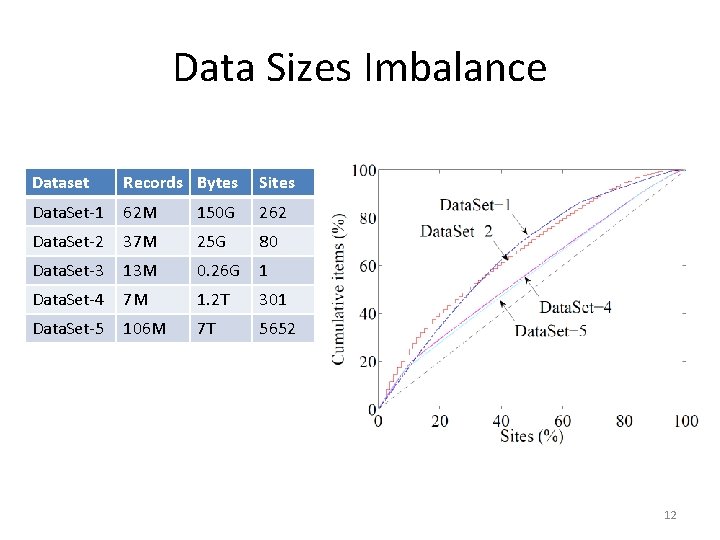
Data Sizes Imbalance Dataset Records Bytes Sites Data. Set-1 62 M 150 G 262 Data. Set-2 37 M 25 G 80 Data. Set-3 13 M 0. 26 G 1 Data. Set-4 7 M 1. 2 T 301 Data. Set-5 106 M 7 T 5652 12

Origins of Data Sizes Imbalance • JOIN SELECT FROM A INNER JOIN B ON A. KEY==B. KEY ORDER BY COL • Lookup Table If the record value of column X is in the lookup table, then return the row • UNPIVOT Input: Output: Col 1 Col 2 1 2, 3 2 3, 9, 8, 13 … (1, 2), (1, 3), (2, 9), … 13

Weighted Sampling Scheme • 14

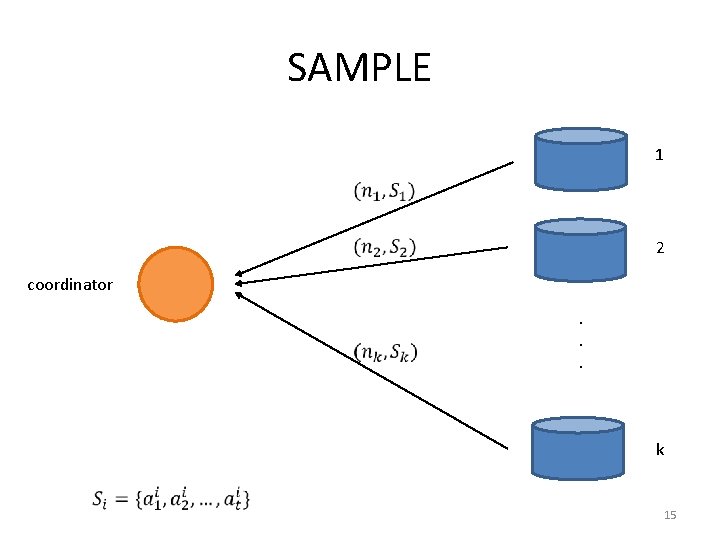
SAMPLE 1 2 coordinator. . . k 15

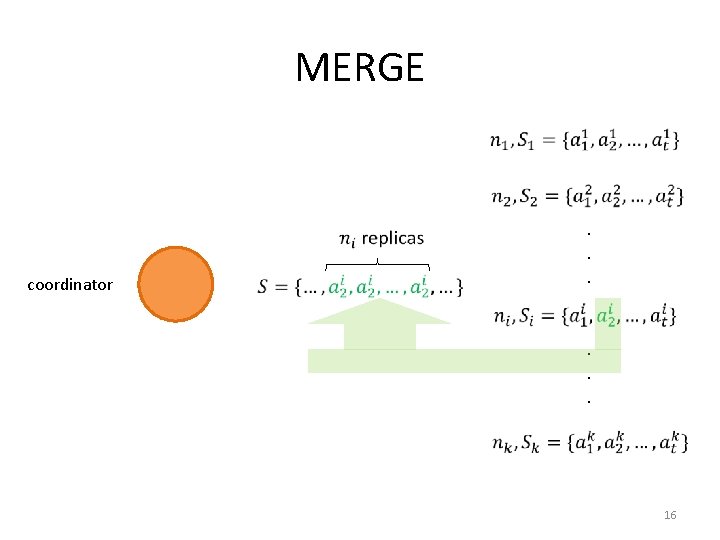
MERGE coordinator . . . 16

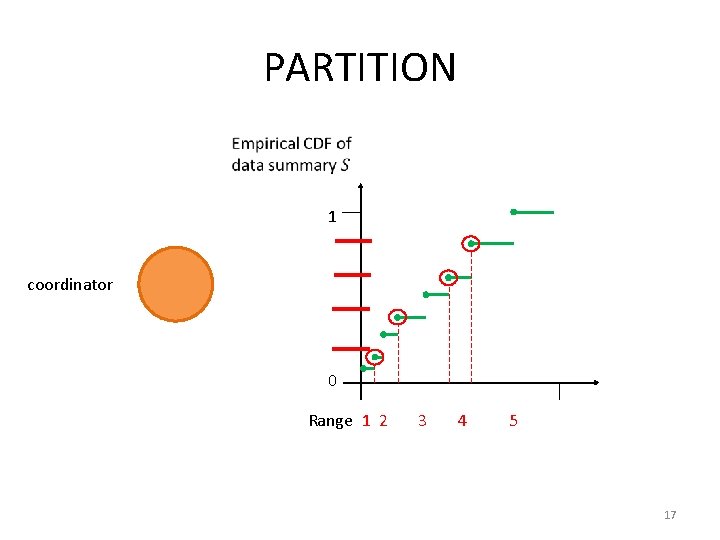
PARTITION 1 coordinator 0 Range 1 2 3 4 5 17

Sufficient Sample Size • 18

Constant Factor Imbalance • 19

Proof Outline • 20

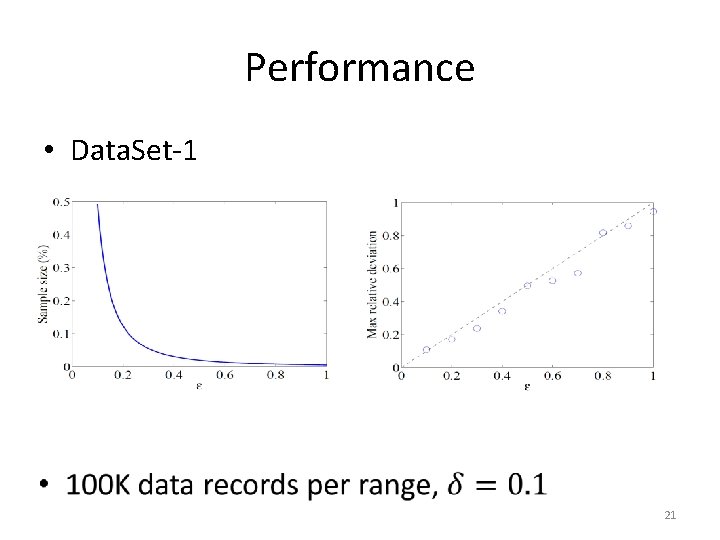
Performance • Data. Set-1 21

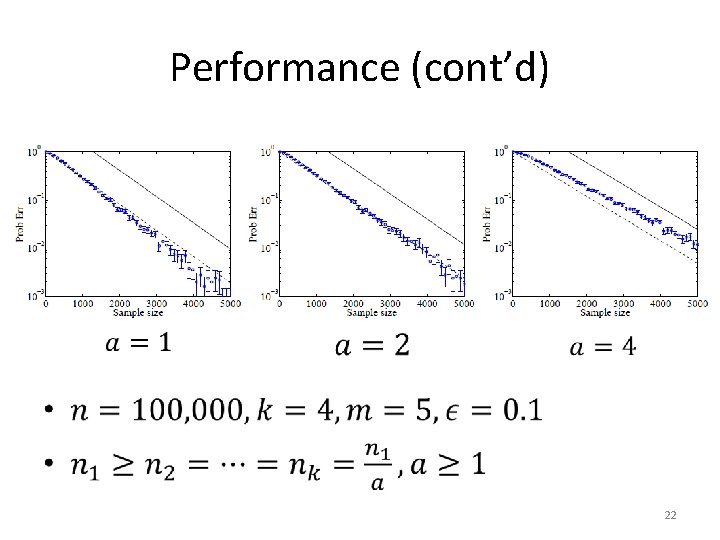
Performance (cont’d) • 22

Summary for Range Partitioning • Novel weighted sampling scheme • Provable performance guarantees • Simple and practical – Coder transfer to Cosmos • More info: Sampling Based Range Partition Methods for Big Data Analytics, V. , Xu, Zhou, MSR-TR-2012 -18, Mar 2012 23

Outline • Range Partition with Fei Xu and Jingren Zhou • Count Tracking with Zhenming Liu and Bozidar Radunovic • Graph Partitioning (def. only) with Charalampos Tsourakakis and Bozidar Radunovic 24

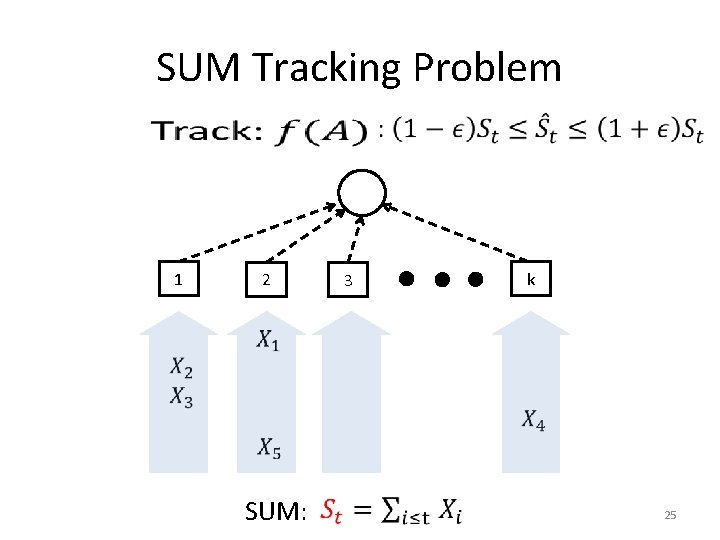
SUM Tracking Problem • 1 2 SUM: 3 k 25

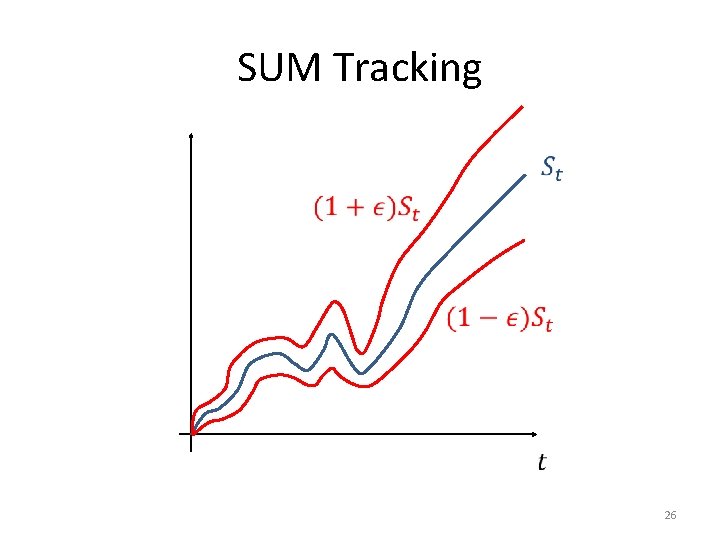
SUM Tracking 26

Applications • input data 27

State of the Art • 28

The Challenge • Q: What are communication cost efficient algorithms for the sum tracking problem with random input streams? – Random permutation – Random i. i. d. – Fractional Brownian motion 29

Communication Complexity Bounds • 30

Communication Complexity Bounds Unknown Drift Case • 31

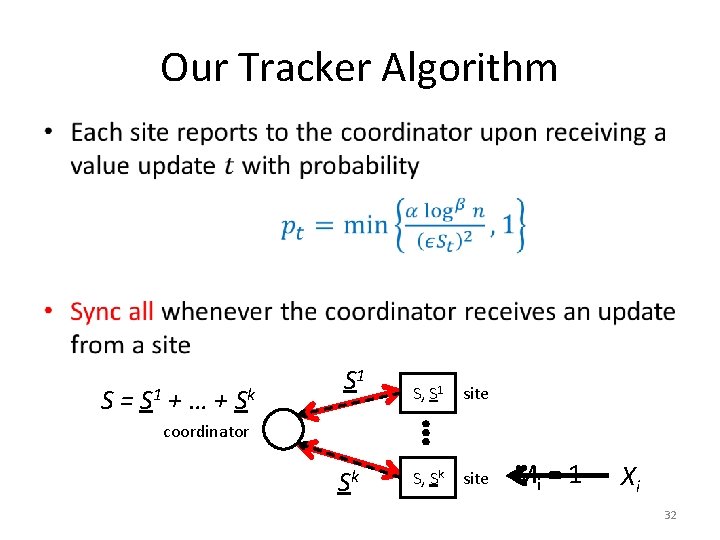
Our Tracker Algorithm • S= S 1 +…+ Sk S 1 S, S 1 site S, Sk site coordinator Sk Mi = 1 Xi 32

Two Applications • Second Frequency Moment • Bayesian Linear Regression 33

App 1: Second Frequency Moment • 34

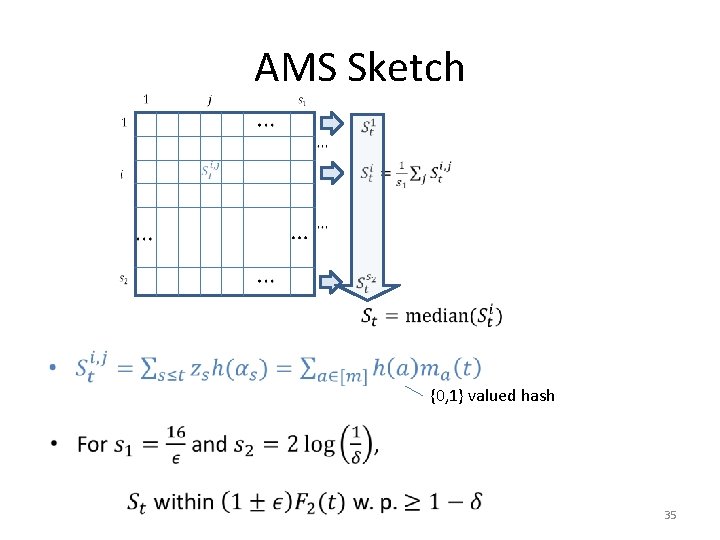
AMS Sketch • {0, 1} valued hash 35

App 1: Second Frequency Moment (cont’d) • 36

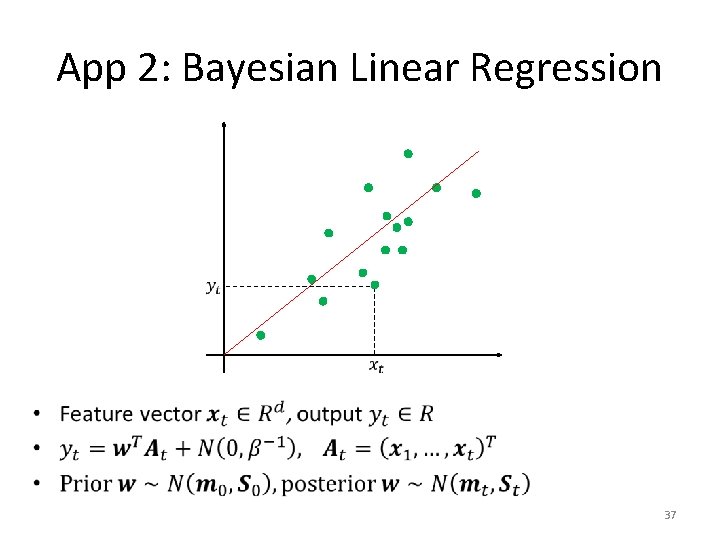
App 2: Bayesian Linear Regression • 37

App 2: Bayesian Linear Regression (cont’d) • 38

Summary for Sum Tracking • Studied the sum tracking problem with nonmonotonic distributed streams under random permutation, random i. i. d. and fractional Brownian motion • Proposed a novel algorithm with nearly optimal communication complexity • Details: ACM PODS 2012 39

Outline • Range Partition with Fei Xu and Jingren Zhou • Count Tracking with Zhenming Liu and Bozidar Radunovic • Graph Partitioning (def. only) with Charalampos Tsourakakis and Bozidar Radunovic 40

Problem • Partition a graph with two objectives – Sparsely connected components – Balanced number of vertices per component • Applications – Parallel processing – Community detection 41

Problem (cont’d) • Requirements 1 2 3 k – Streaming algorithm – Single pass / incremental – Efficient computing • Desired – Approximation guarantees – Average-case efficient 42

Summary for Graph Partitioning • Designed a streaming algorithm whose average-case performance appears superior to any of previously proposed online heuristics • Provable approximation guarantees • More details available soon 43