Sampling and Aliasing Kurt Akeley CS 248 Lecture

Sampling and Aliasing Kurt Akeley CS 248 Lecture 3 2 October 2007 http: //graphics. stanford. edu/courses/cs 248 -07/

Aliasing Aliases are low frequencies in a rendered image that are due to higher frequencies in the original image. CS 248 Lecture 3 Kurt Akeley, Fall 2007

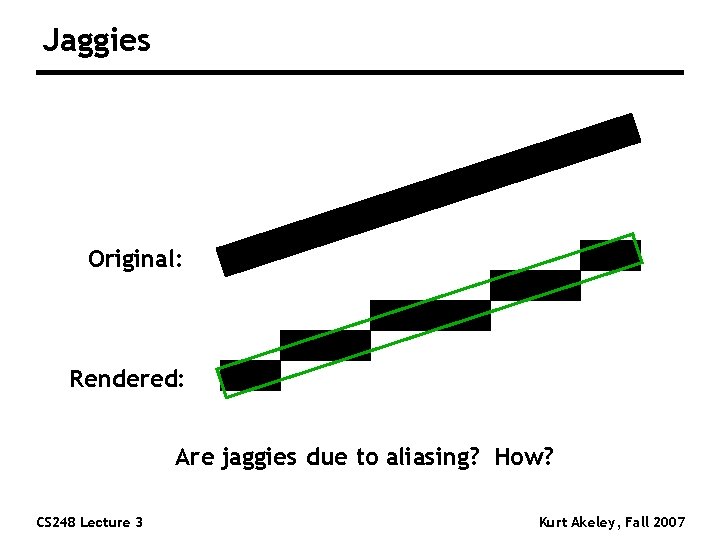
Jaggies Original: Rendered: Are jaggies due to aliasing? How? CS 248 Lecture 3 Kurt Akeley, Fall 2007

Demo CS 248 Lecture 3 Kurt Akeley, Fall 2007

What is a point sample (aka sample)? An evaluation n At an infinitesimal point (2 -D) n Or along a ray (3 -D) What is evaluated n Inclusion (2 -D) or intersection (3 -D) n Attributes such as distance and color CS 248 Lecture 3 Kurt Akeley, Fall 2007

Why point samples? Clear and unambiguous semantics Matches theory well (as we’ll see) Supports image assembly in the framebuffer n will need to resolve visibility based on distance, and this works well with point samples Anything else just puts the problem off n Exchange one large, complex scene for many small, complex scenes CS 248 Lecture 3 Kurt Akeley, Fall 2007

Fourier theory “Fourier’s theorem is not only one of the most beautiful results of modern analysis, but it may be said to furnish an indispensable instrument in the treatment of nearly every recondite question in modern physics. ” -- Lord Kelvin CS 248 Lecture 3 Kurt Akeley, Fall 2007

Reference sources Marc Levoy’s notes Ronald N. Bracewell, The Fourier Transform and its Applications, Second Edition, Mc. Graw-Hill, Inc. , 1978. Private conversations with Pat Hanrahan MATLAB CS 248 Lecture 3 Kurt Akeley, Fall 2007

Ground rules You don’t have to be an engineer to get this n We’re looking to develop instinct / understanding n Not to be able to do the mathematics We’ll make minimal use of equations n No integral equations n No complex numbers Plots will be consistent n Tick marks at unit distances n Signal on left, Fourier transform on the right CS 248 Lecture 3 Kurt Akeley, Fall 2007

Dimensions 1 -D n Audio signal (time) n Generic examples (x) n Image (x and y) n Animation (x, y, and time) 2 -D 3 -D All examples in this presentation are 1 -D CS 248 Lecture 3 Kurt Akeley, Fall 2007

Fourier series Any periodic function can be exactly represented by a (typically infinite) sum of harmonic sine and cosine functions. Harmonics are integer multiples of the fundamental frequency CS 248 Lecture 3 Kurt Akeley, Fall 2007

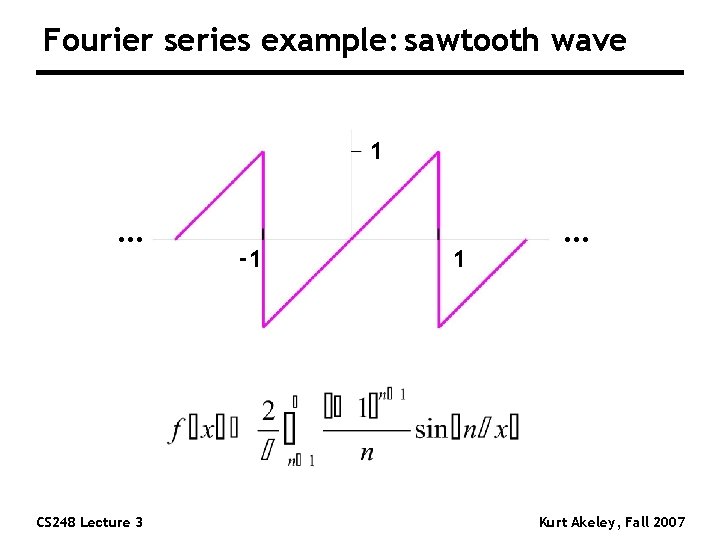
Fourier series example: sawtooth wave 1 … CS 248 Lecture 3 -1 1 … Kurt Akeley, Fall 2007

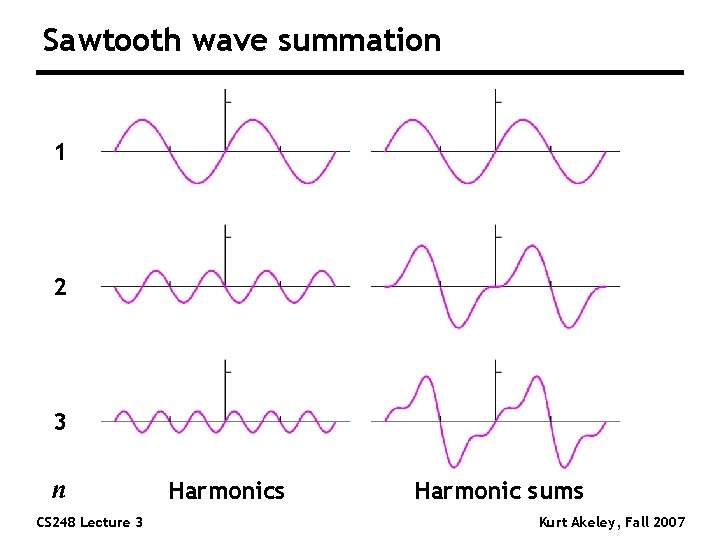
Sawtooth wave summation 1 2 3 n CS 248 Lecture 3 Harmonics Harmonic sums Kurt Akeley, Fall 2007

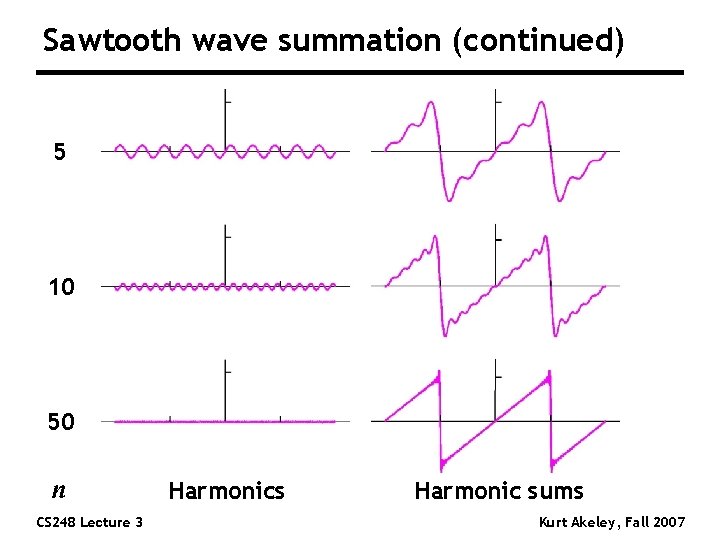
Sawtooth wave summation (continued) 5 10 50 n CS 248 Lecture 3 Harmonics Harmonic sums Kurt Akeley, Fall 2007

Fourier integral Any function (that matters in graphics) can be exactly represented by an integration of sine and cosine functions. Continuous, not harmonic But the notion of harmonics will continue to be useful CS 248 Lecture 3 Kurt Akeley, Fall 2007

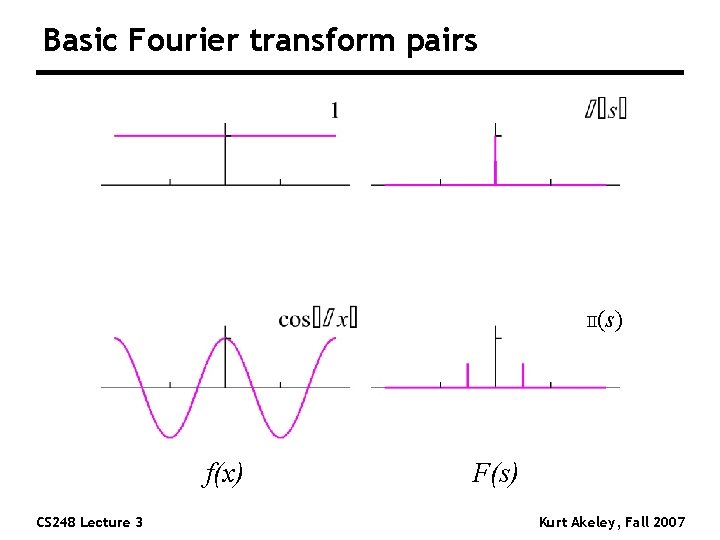
Basic Fourier transform pairs II(s) f(x) CS 248 Lecture 3 F(s) Kurt Akeley, Fall 2007

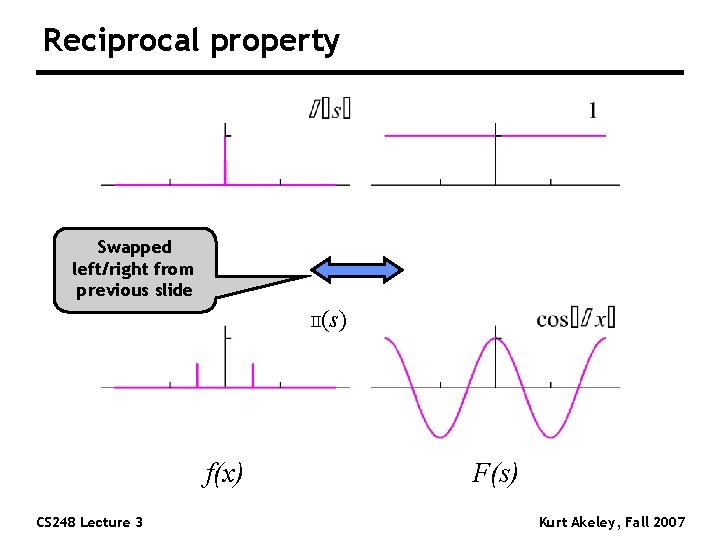
Reciprocal property Swapped left/right from previous slide II(s) f(x) CS 248 Lecture 3 F(s) Kurt Akeley, Fall 2007

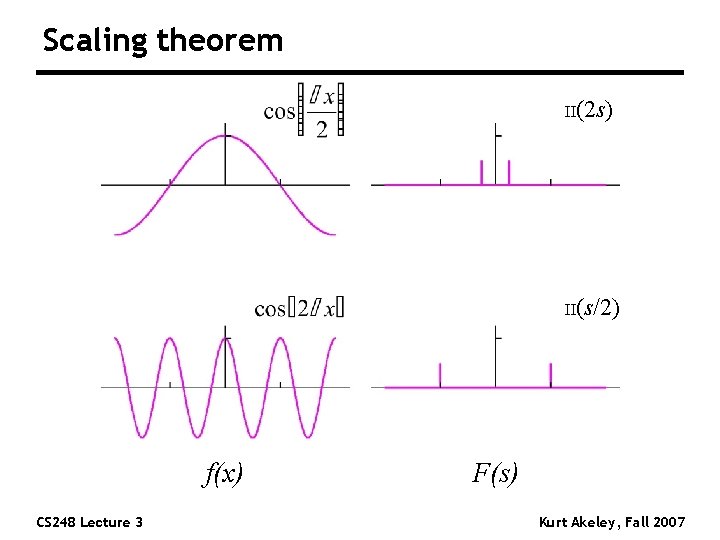
Scaling theorem II(2 s) II(s/2) f(x) CS 248 Lecture 3 F(s) Kurt Akeley, Fall 2007

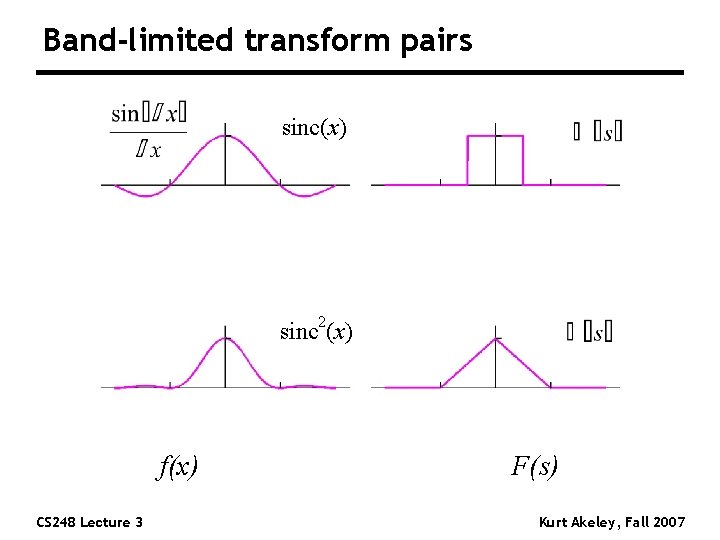
Band-limited transform pairs sinc(x) sinc 2(x) f(x) CS 248 Lecture 3 F(s) Kurt Akeley, Fall 2007

Finite / infinite extent If one member of the transform pair is finite, the other is infinite n Band-limited infinite spatial extent n Finite spatial extent infinite spectral extent CS 248 Lecture 3 Kurt Akeley, Fall 2007

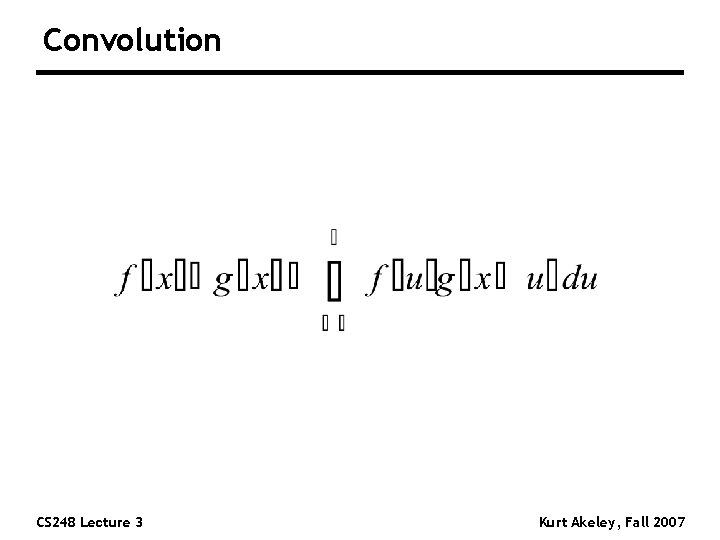
Convolution CS 248 Lecture 3 Kurt Akeley, Fall 2007

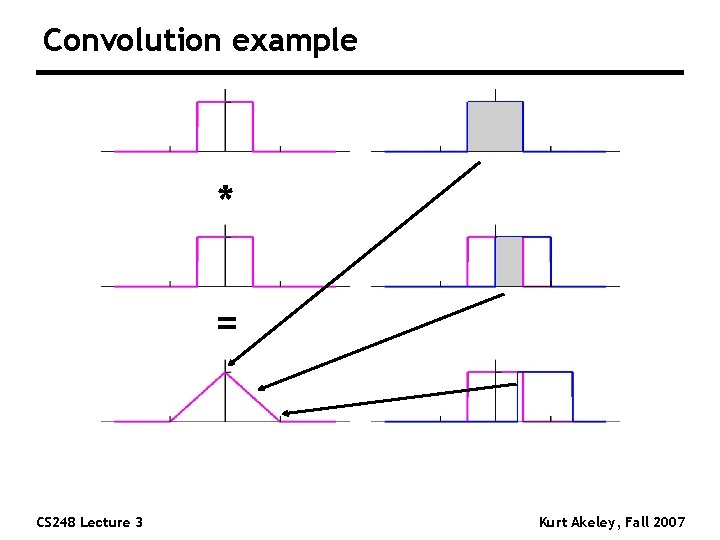
Convolution example * = CS 248 Lecture 3 Kurt Akeley, Fall 2007

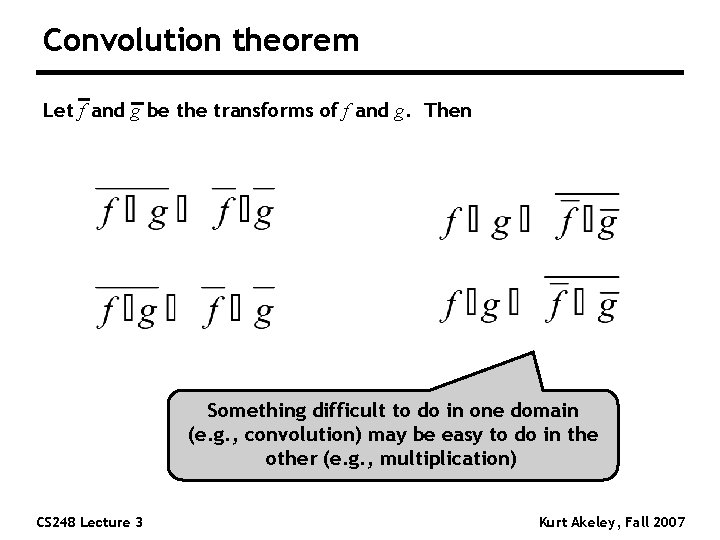
Convolution theorem Let f and g be the transforms of f and g. Then Something difficult to do in one domain (e. g. , convolution) may be easy to do in the other (e. g. , multiplication) CS 248 Lecture 3 Kurt Akeley, Fall 2007

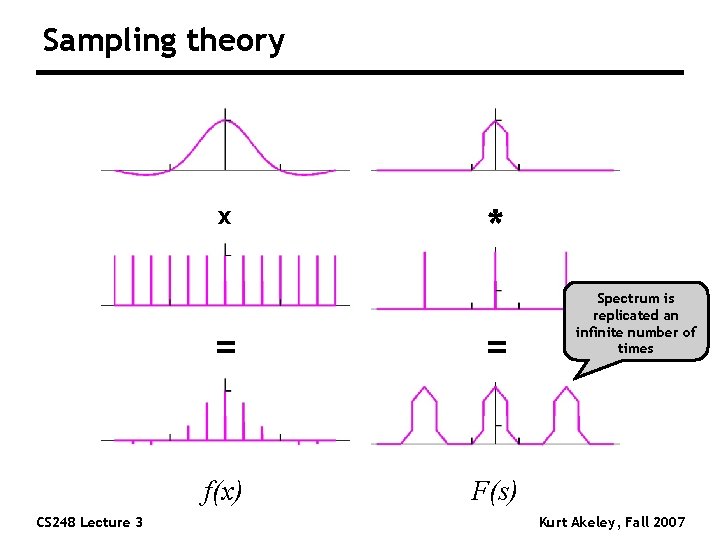
Sampling theory x CS 248 Lecture 3 * = = f(x) F(s) Spectrum is replicated an infinite number of times Kurt Akeley, Fall 2007

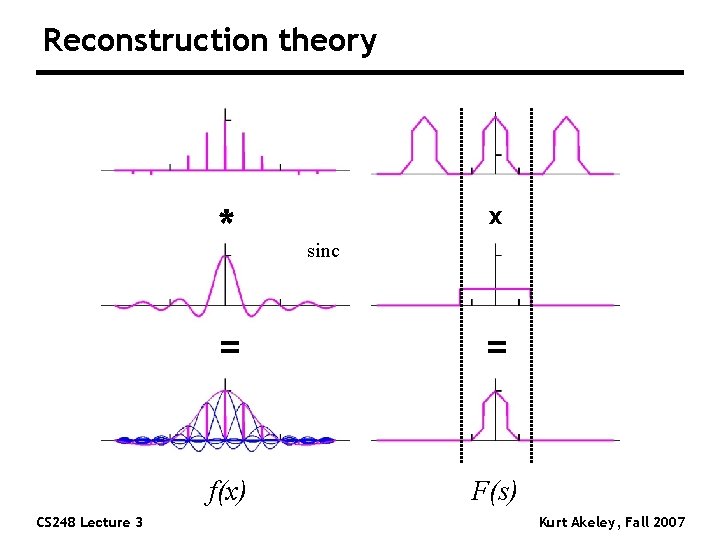
Reconstruction theory * CS 248 Lecture 3 x sinc = = f(x) F(s) Kurt Akeley, Fall 2007

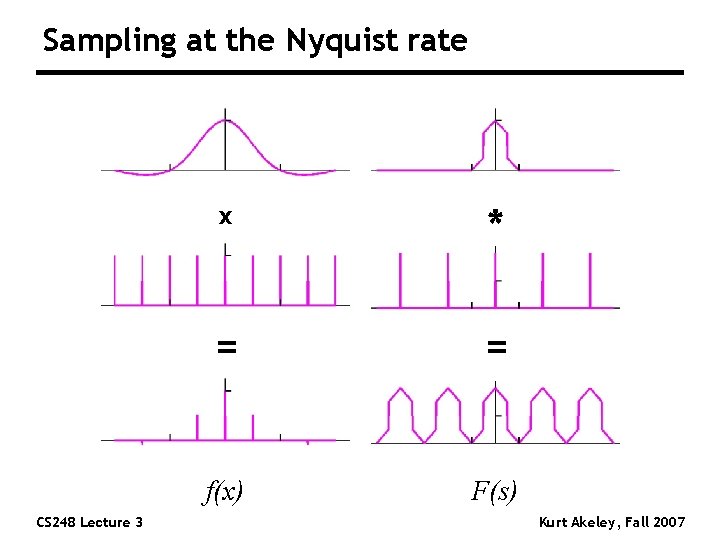
Sampling at the Nyquist rate CS 248 Lecture 3 x * = = f(x) F(s) Kurt Akeley, Fall 2007

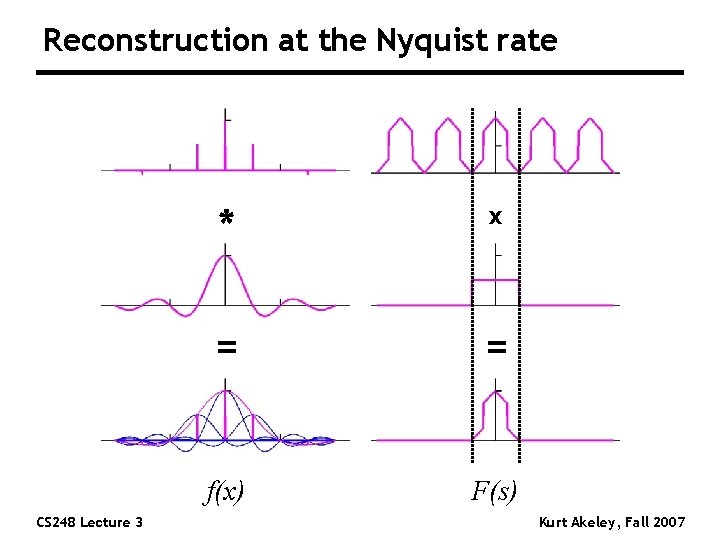
Reconstruction at the Nyquist rate CS 248 Lecture 3 * x = = f(x) F(s) Kurt Akeley, Fall 2007

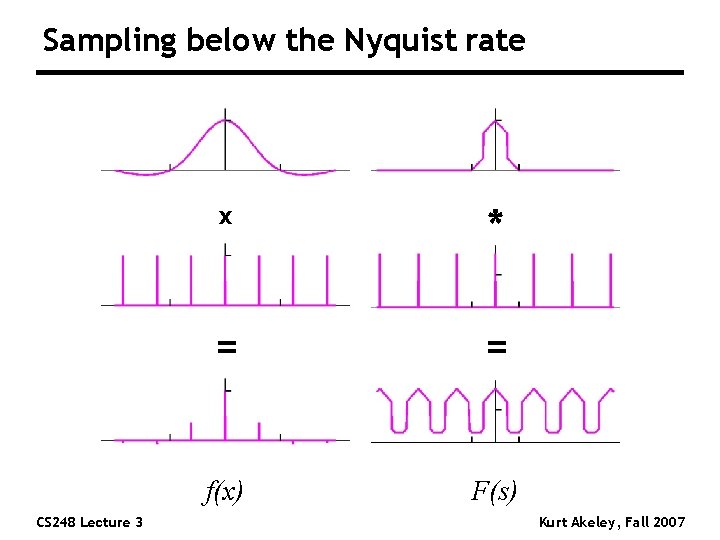
Sampling below the Nyquist rate CS 248 Lecture 3 x * = = f(x) F(s) Kurt Akeley, Fall 2007

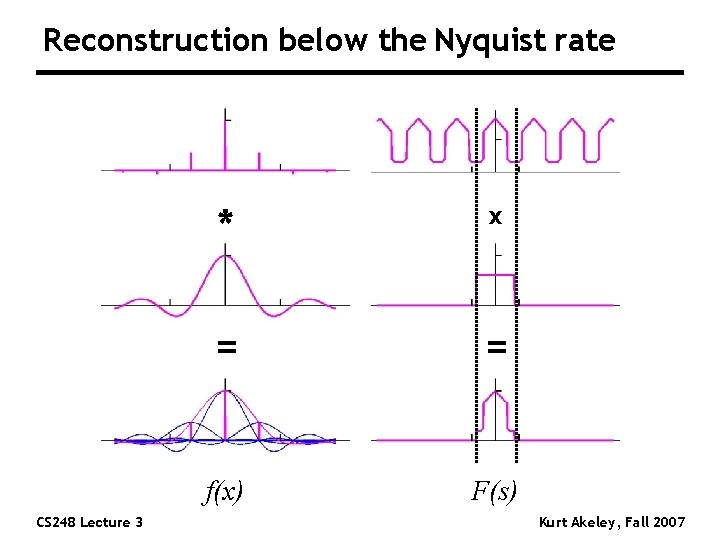
Reconstruction below the Nyquist rate CS 248 Lecture 3 * x = = f(x) F(s) Kurt Akeley, Fall 2007

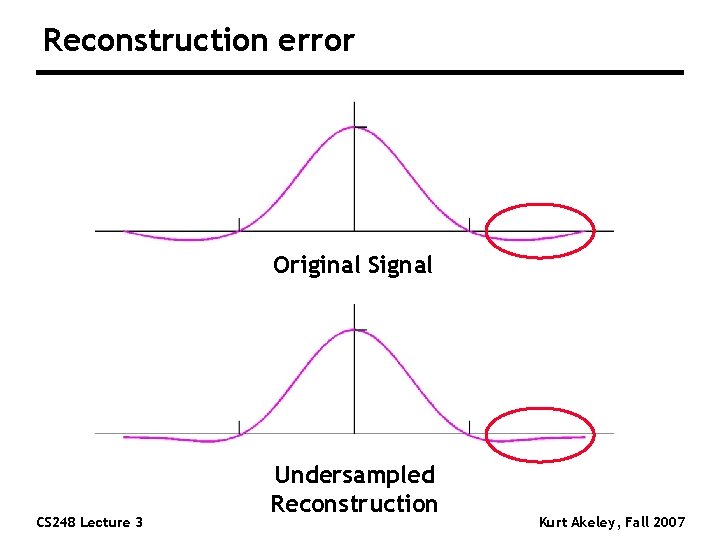
Reconstruction error Original Signal CS 248 Lecture 3 Undersampled Reconstruction Kurt Akeley, Fall 2007

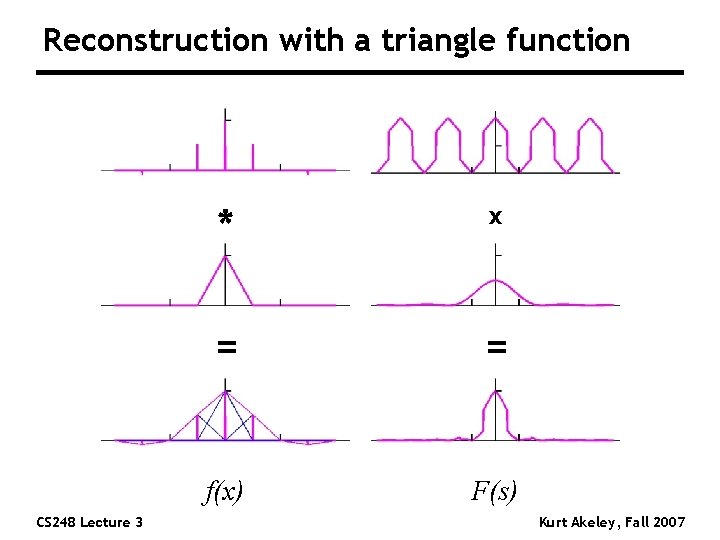
Reconstruction with a triangle function CS 248 Lecture 3 * x = = f(x) F(s) Kurt Akeley, Fall 2007

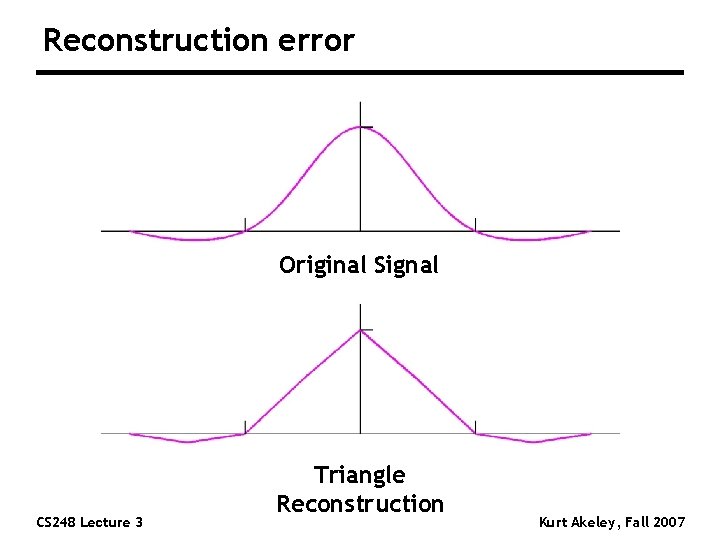
Reconstruction error Original Signal CS 248 Lecture 3 Triangle Reconstruction Kurt Akeley, Fall 2007

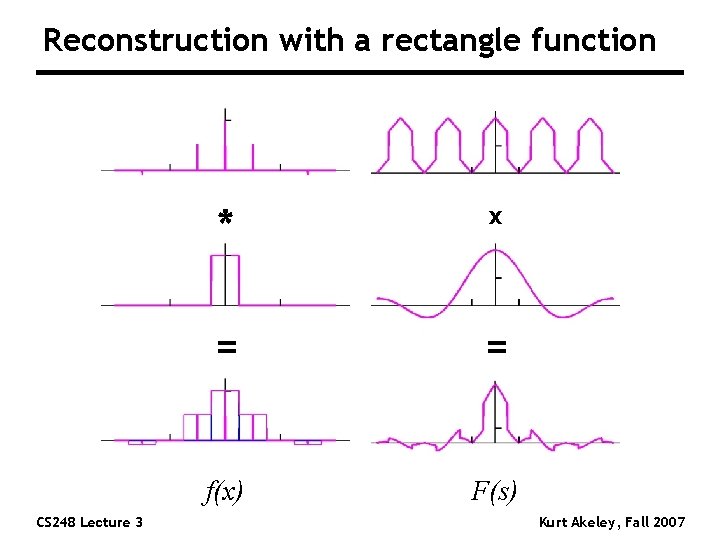
Reconstruction with a rectangle function CS 248 Lecture 3 * x = = f(x) F(s) Kurt Akeley, Fall 2007

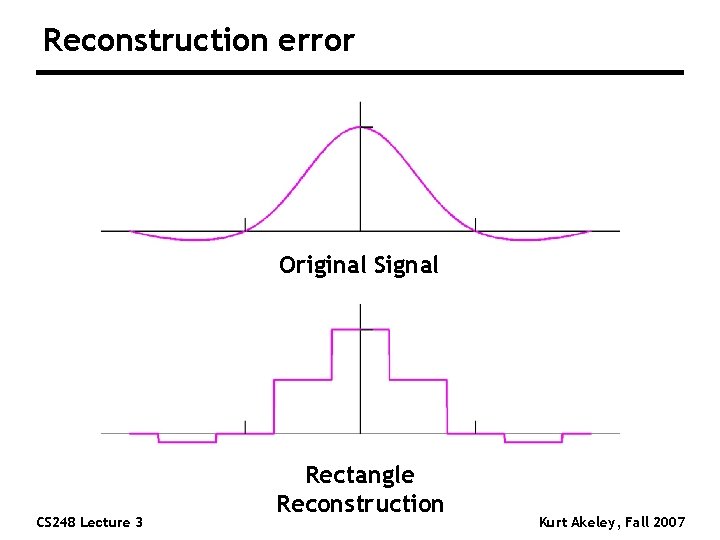
Reconstruction error Original Signal CS 248 Lecture 3 Rectangle Reconstruction Kurt Akeley, Fall 2007

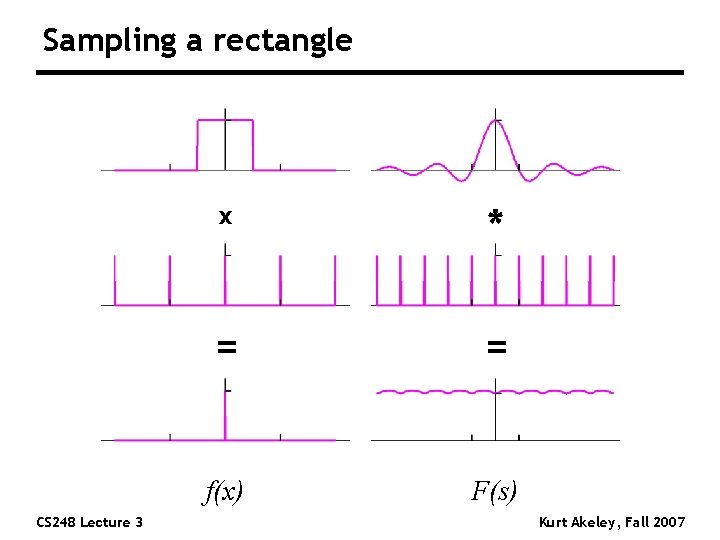
Sampling a rectangle CS 248 Lecture 3 x * = = f(x) F(s) Kurt Akeley, Fall 2007

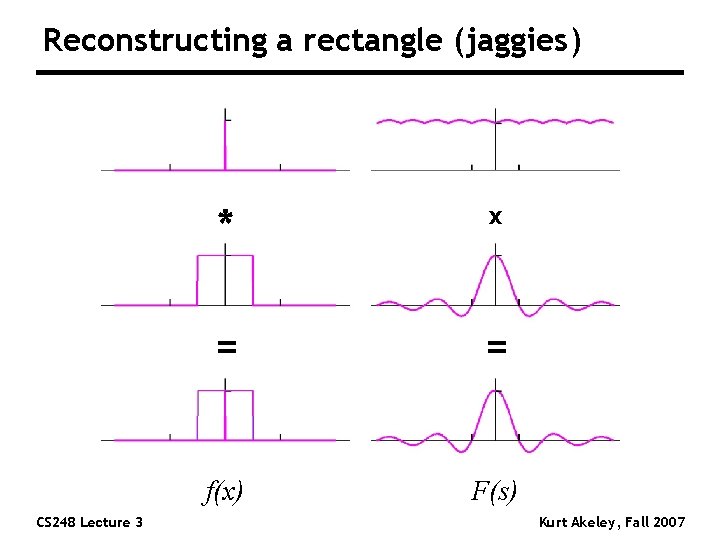
Reconstructing a rectangle (jaggies) CS 248 Lecture 3 * x = = f(x) F(s) Kurt Akeley, Fall 2007

Sampling and reconstruction Aliasing is caused by n Sampling below the Nyquist rate, n Improper reconstruction, or n Both We can distinguish between n Aliasing of fundamentals (demo) n Aliasing of harmonics (jaggies) CS 248 Lecture 3 Kurt Akeley, Fall 2007

Summary Jaggies matter n Create false cues n Violate rule 1 Sampling is done at points (2 -D) or along rays (3 -D) n Sufficient for depth sorting n Matches theory Fourier theory explains jaggies as aliasing. For correct reconstruction: n Signal must be band-limited n Sampling must be at or above Nyquist rate n Reconstruction must be done with a sinc function CS 248 Lecture 3 Kurt Akeley, Fall 2007

Assignments Before Thursday’s class, read n Fv. D 3. 17 Antialiasing Project 1: n Breakout: a simple interactive game n Demos Wednesday 10 October CS 248 Lecture 3 Kurt Akeley, Fall 2007

End CS 248 Lecture 3 Kurt Akeley, Fall 2007