Sampling and Aliasing Gilad Lerman Math 5467 stealing

Sampling and Aliasing Gilad Lerman Math 5467 (stealing slides from Gonzalez & Woods, and Efros)

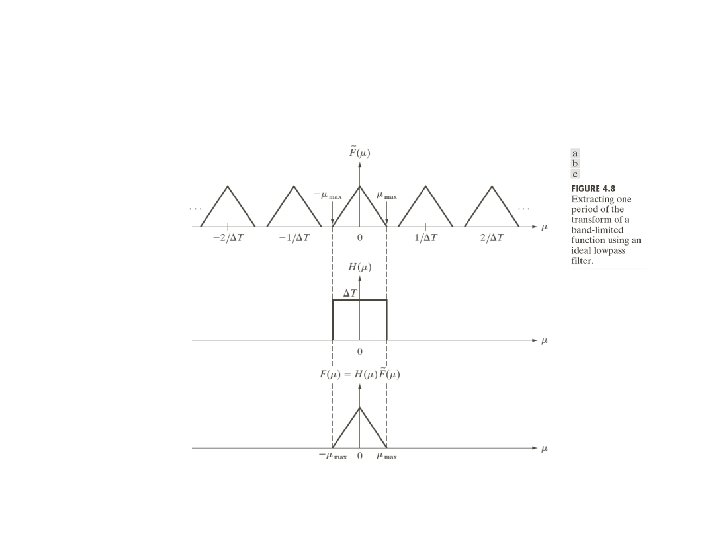
The Sampling Theorem: If f is in L 1( ) & supported on [-B 0, B 0], then Recall Proof: We view as (2 B 0)-periodic function with coefficients: At last, find f using IFT and using FS of

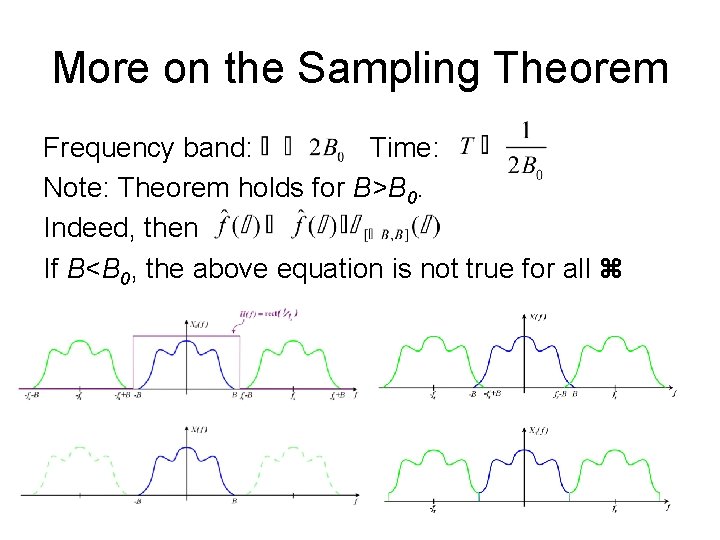
More on the Sampling Theorem Frequency band: Time: Note: Theorem holds for B>B 0. Indeed, then If B<B 0, the above equation is not true for all

Sampling Theorem (meaning) • Interpretation: If a function f(t) contains no frequencies higher than W cps, it is completely determined by giving its ordinates at a series of points spaced 1/(2 W) seconds apart • Remark: For L 1 function a freq. = W is fine but for more general functions we need > W…

Simple Example (not L 1) Assume a cosine (it is not L 1( ) but will be instrumental) Freq: a (“& -a”), Freq Band: =[-a, a], Time: 1/(2 a) Here one needs B>B 0 (B=B 0 doesn’t work) Example: for all 3 functions freq: 0. 5, time: 1 The sampled function has different aliases…

Aliasing • If the sampling condition is not satisfied, frequencies will overlap (high freq → low freq) • The reconstructed signal is said to be an alias of the original signal

Example: Increased Frequency Input signal: Related Image: Matlab output: Picket fence receding Into the distance will produce aliasing… x = 0: . 05: 5; imagesc(sin((2. ^x). *x))

One more example at the Fourier domain

Aliasing in Images (Fourier domain)

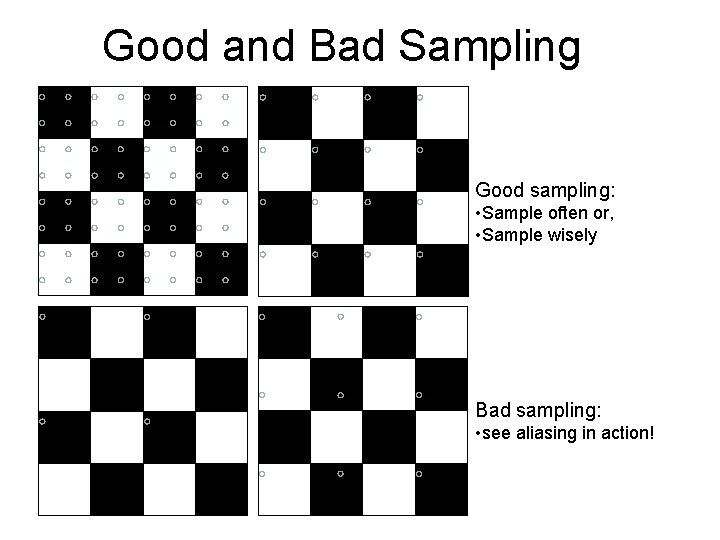
Good and Bad Sampling Good sampling: • Sample often or, • Sample wisely Bad sampling: • see aliasing in action!

Texture makes its worse (high frequencies)

Even worse for synthetic images Slide by Steve Seitz

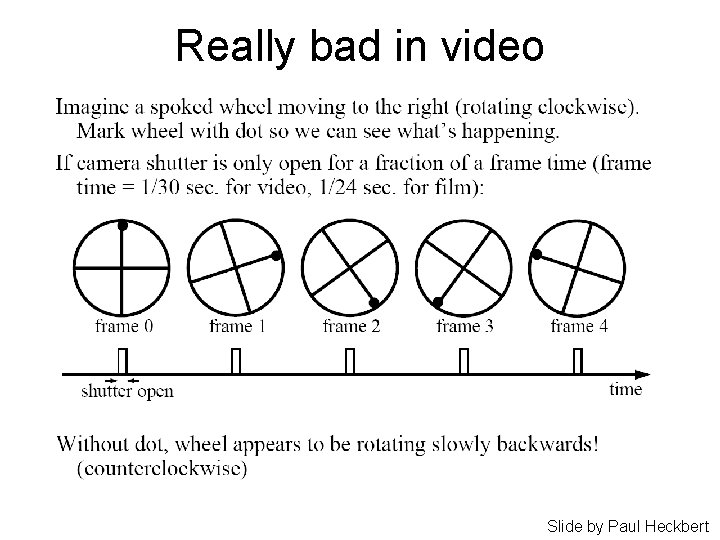
Really bad in video Slide by Paul Heckbert

Wheels of Wagons in Westerns

Moiré pattern • Definition: Interference pattern created, e. g. , when two grids are overlaid at an angle, or when they have slightly different mesh sizes. • In images produced e. g. , when scanning a halftone picture or due to undersampling a fine regular pattern.

Moiré pattern due to undersampling Original image downsampled image

Antialiasing • What can be done? Sampling rate ≥ 2 * max frequency in the image 1. Raise sampling rate by oversampling – Sample at k times the resolution – continuous signal: easy – discrete signal: need to interpolate • 2. Lower the max frequency by prefiltering – Smooth the signal enough – Works on discrete signals • 3. Improve sampling quality with better sampling – – Nyquist is best case! Stratified sampling Importance sampling Relies on domain knowledge

Gaussian pre-filtering G 1/8 G 1/4 Gaussian 1/2 • Solution: filter the image, then subsample – Filter size should double for each ½ size reduction.

Subsampling with Gaussian pre-filtering Gaussian 1/2 G 1/4 G 1/8

Compare with. . . 1/2 1/4 (2 x zoom) 1/8 (4 x zoom)

Correcting some Moiré patterns