Sample Electronic Lesson Copyright Prof J Pieter H

Sample – Electronic Lesson Copyright Prof J Pieter H van Wyk © Direct-Science

VECTORS AND SCALARS © Direct-Science 2

VECTORS AND SCALARS: Resultant velocity A plane flies at 550 km. h-1 Complete a vector from town A to town B diagram of the above that is in a direction of 00 motion and indicate: and 1200 km from town A. i) direction of wind During the flight the plane ii) direction in which plane experiences a wind that must aim to reach town B blows at 150 km. h-1 in a iii) resultant velocity of direction 900. The plane. has to land at B. © Direct-Science 3

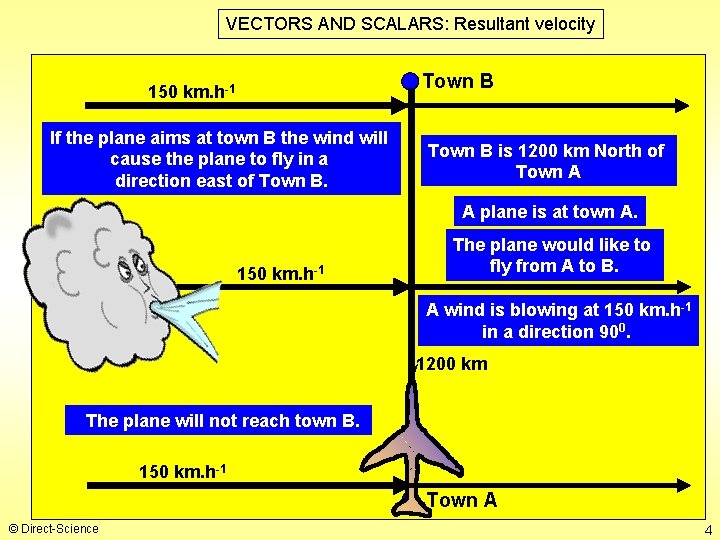
VECTORS AND SCALARS: Resultant velocity Town B 150 km. h-1 If the plane aims at town B the wind will cause the plane to fly in a direction east of Town B is 1200 km North of Town A A plane is at town A. 150 km. h-1 The plane would like to fly from A to B. A wind is blowing at 150 km. h-1 in a direction 900. 1200 km The plane will not reach town B. 150 km. h-1 Town A © Direct-Science 4

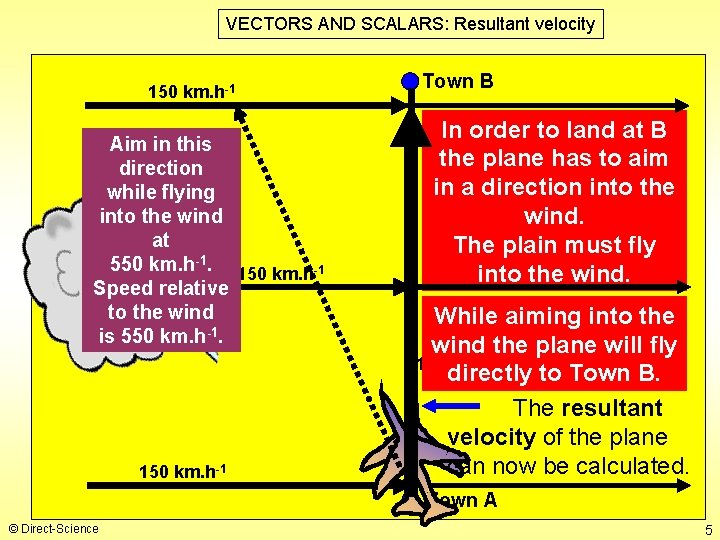
VECTORS AND SCALARS: Resultant velocity 150 km. h-1 Aim in this direction while flying into the wind at 550 km. h-1. 150 km. h-1 Speed relative to the wind is 550 km. h-1. 150 km. h-1 Town B In order to land at B the plane has to aim in a direction into the wind. The plain must fly into the wind. While aiming into the wind the plane will fly 1200 km directly to Town B. The resultant velocity of the plane can now be calculated. Town A © Direct-Science 5

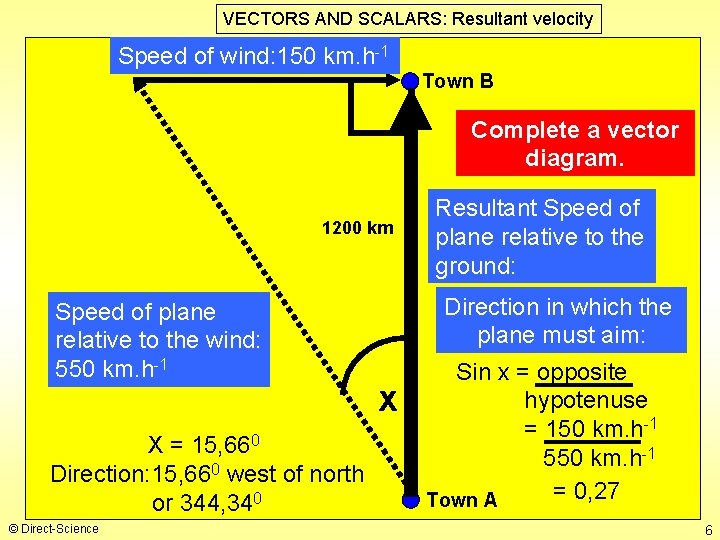
VECTORS AND SCALARS: Resultant velocity Speed of wind: 150 km. h-1 Town B Complete a vector diagram. 1200 km Speed of plane relative to the wind: 550 km. h-1 X = 15, 660 Direction: 15, 660 west of north or 344, 340 © Direct-Science Resultant Speed of plane relative to the ground: Direction in which the plane must aim: x Sin x = opposite hypotenuse = 150 km. h-1 550 km. h-1 = 0, 27 Town A 6

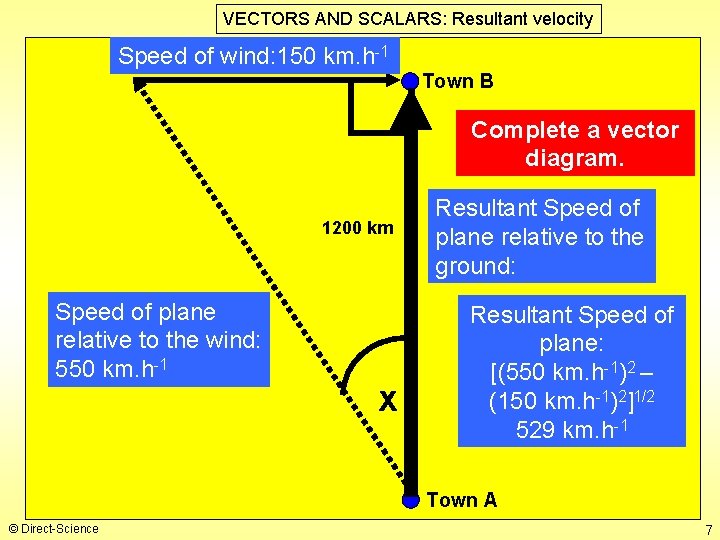
VECTORS AND SCALARS: Resultant velocity Speed of wind: 150 km. h-1 Town B Complete a vector diagram. 1200 km Speed of plane relative to the wind: 550 km. h-1 x Resultant Speed of plane relative to the ground: Resultant Speed of plane: [(550 km. h-1)2 – (150 km. h-1)2]1/2 529 km. h-1 Town A © Direct-Science 7

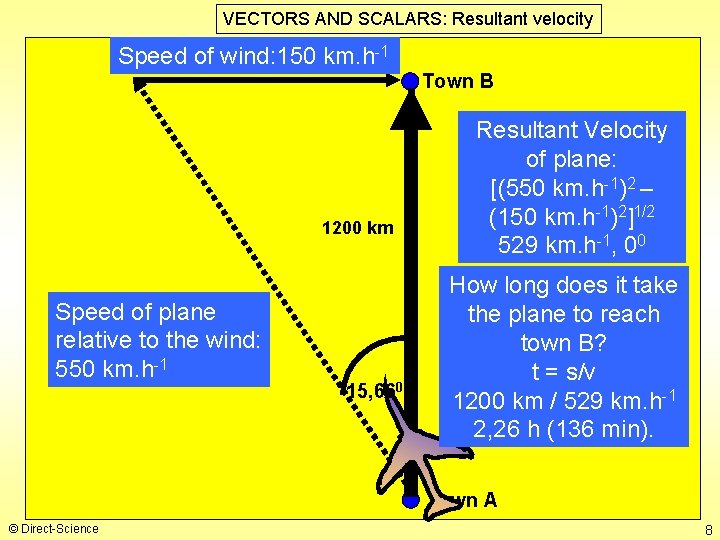
VECTORS AND SCALARS: Resultant velocity Speed of wind: 150 km. h-1 Town B 1200 km Speed of plane relative to the wind: 550 km. h-1 15, 660 Resultant Velocity of plane: [(550 km. h-1)2 – (150 km. h-1)2]1/2 529 km. h-1, 00 How long does it take the plane to reach town B? t = s/v 1200 km / 529 km. h-1 2, 26 h (136 min). Town A © Direct-Science 8

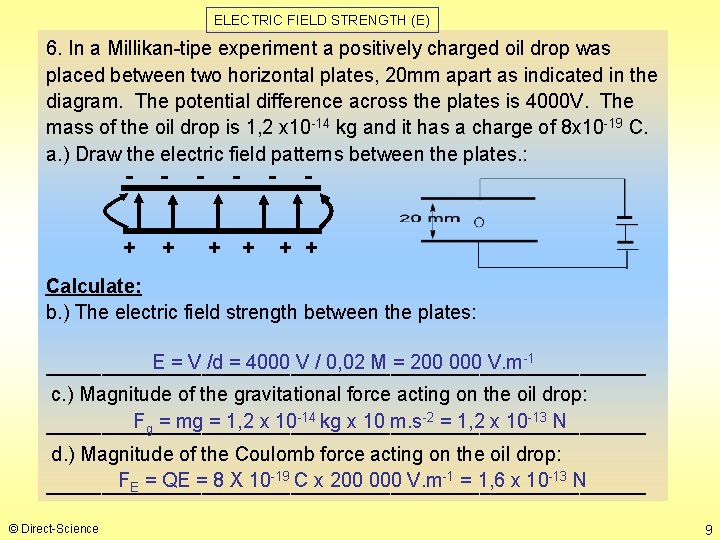
ELECTRIC FIELD STRENGTH (E) 6. In a Millikan-tipe experiment a positively charged oil drop was placed between two horizontal plates, 20 mm apart as indicated in the diagram. The potential difference across the plates is 4000 V. The mass of the oil drop is 1, 2 x 10 -14 kg and it has a charge of 8 x 10 -19 C. a. ) Draw the electric field patterns between the plates. : - - + + Calculate: b. ) The electric field strength between the plates: E = V /d = 4000 V / 0, 02 M = 200 000 V. m-1 ___________________________ c. ) Magnitude of the gravitational force acting on the oil drop: Fg = mg = 1, 2 x 10 -14 kg x 10 m. s-2 = 1, 2 x 10 -13 N ___________________________ d. ) Magnitude of the Coulomb force acting on the oil drop: FE = QE = 8 X 10 -19 C x 200 000 V. m-1 = 1, 6 x 10 -13 N ___________________________ © Direct-Science 9

ELECTRIC FIELD STRENGTH (E) e. ) The oil drop is being observed with a microscope. Explain the behavior of the oil drop: Two forces are acting on the oil drop. Upward electrostatic force: 1, 6. 10 -13 N Oil drop Downward gravitational force: 1, 3. 10 -13 N Upward force is stronger than downward force. Oil drop experiences an upward resultant force (FRES) and according to Newton’s second Law the oil drop will accelerate in direction of the resultant force (upwards). © Direct-Science 10

ELECTRIC FIELD STRENGTH (E) f. ) Describe two methods that can be applied to keep the oil drop stationary: - - - Upward electrostatic force: 1, 6. 10 -13 N = F= QE Oil drop Downward gravitational force: 1, 3. 10 -13 N = F = mg + + + To keep the object stationary the forces must be in equilibrium. The following are possible ways to balance these forces: (i) Increase the downward force – mg (i) m - mass of the particle is fixed and is not allowed to be changed. (ii) g – constant at 10 m. s-2 and cannot be changed. Downward force cannot be changed. © Direct-Science 11

ELECTRIC FIELD STRENGTH (E) f. ) Describe two methods that can be applied to keep the oil drop stationary: - - - Upward electrostatic force: 1, 6. 10 -13 N = F= QE Oil drop Downward gravitational force: 1, 3. 10 -13 N = F = mg + + + To keep the object stationary the forces must be in equilibrium. The following are possible ways to balance these forces: (i) Decrease the upward force – QE (i) Q – charge on the particle is fixed and is not allowed to be changed. (ii) E – electric field strength is determined by the distance (d) between the parallel plates as well as the potential difference over these plates (V) : E = V/d © Direct-Science 12

ELECTRIC FIELD STRENGTH (E) f. ) Describe two methods that can be applied to keep the oil drop stationary: - - - Upward electrostatic force: 1, 6. 10 -13 N = F= QE Oil drop Downward gravitational force: 1, 3. 10 -13 N = F = mg + + + E = V/d If V is decreased (without changing d), E will decrease and upward force will decrease. If d is increased (without changing V), E will decrease and upward force will decrease. To keep particle stationary: (i) Decrease potential difference over plates. (ii) Increase distance between plates. © Direct-Science 13

CURRENT ELECTRICITY © Direct-Science 14

CURRENT ELECTRICITY State Ohm’s Law: (1) The current (I) in a metallic conductor is directly proportional to the potential difference (V) across its ends, provided that the temperature remains constant. Ohm’s Law Equation: (2) V I (V = IR) Potential difference: Resistance: Electric Current: Symbol: ____(3) V Symbol: _______(6) R Symbol: ____(9) I Formula: ____(4) V = IR Formula: I_______(7) = V/R Formula: ____(10) I = V/R Unit: _____(5) Volt Unit: _____(8) Ohm Unit: ______(11) Ampere © Direct-Science 15

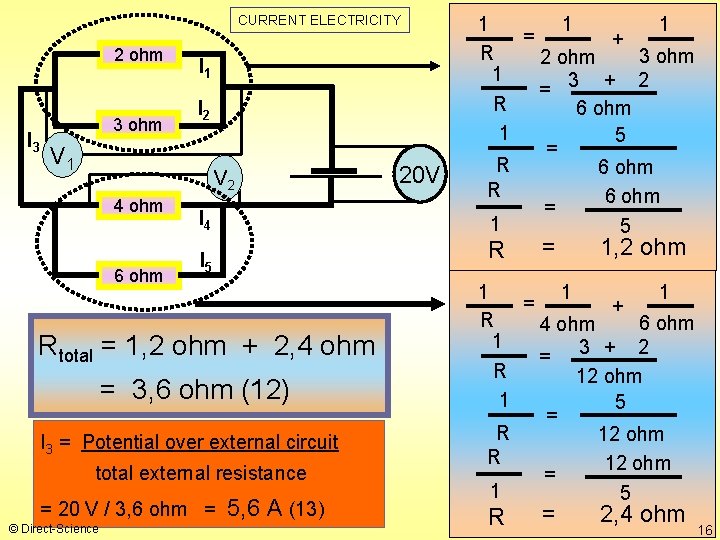
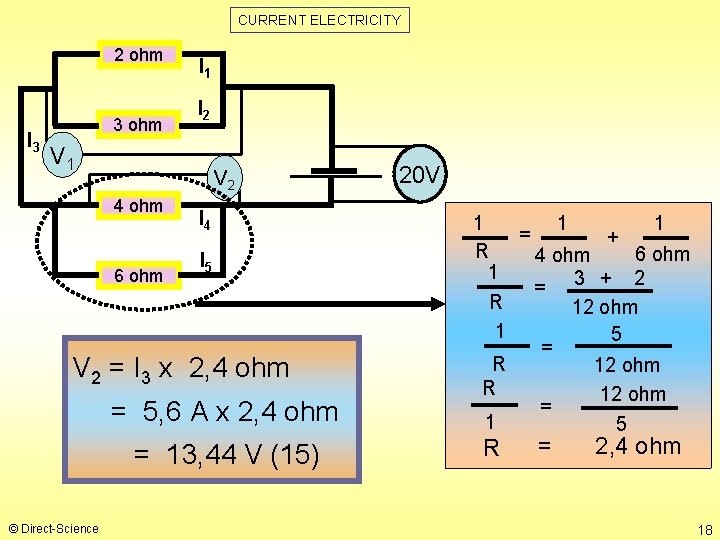
CURRENT ELECTRICITY 2 ohm I 3 3 ohm I 1 I 2 V 1 V 2 4 ohm 6 ohm I 4 R I 5 Rtotal = 1, 2 ohm + 2, 4 ohm = 3, 6 ohm (12) I 3 = Potential over external circuit total external resistance = 20 V / 3, 6 ohm = © Direct-Science 20 V 1 1 1 = + R 3 ohm 2 ohm 1 = 3 + 2 R 6 ohm 1 5 = R 6 ohm = 1 5 5, 6 A (13) = 1, 2 ohm 1 1 1 = + R 6 ohm 4 ohm 1 = 3 + 2 R 12 ohm 1 5 = R 12 ohm = 1 5 R = 2, 4 ohm 16

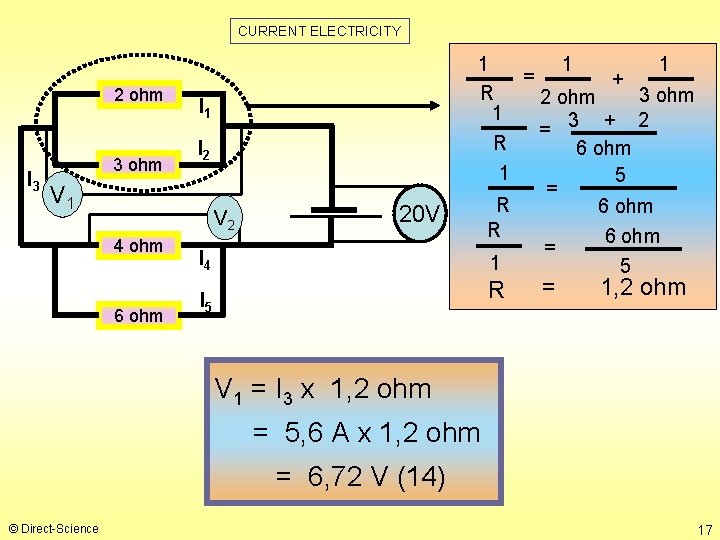
CURRENT ELECTRICITY 2 ohm I 3 3 ohm I 1 I 2 V 1 V 2 4 ohm 6 ohm 20 V I 4 1 1 1 = + R 3 ohm 2 ohm 1 = 3 + 2 R 6 ohm 1 5 = R 6 ohm = 1 5 R I 5 = 1, 2 ohm V 1 = I 3 x 1, 2 ohm = 5, 6 A x 1, 2 ohm = 6, 72 V (14) © Direct-Science 17

CURRENT ELECTRICITY 2 ohm I 3 3 ohm I 1 I 2 V 1 V 2 4 ohm 6 ohm I 4 I 5 V 2 = I 3 x 2, 4 ohm = 5, 6 A x 2, 4 ohm = 13, 44 V (15) © Direct-Science 20 V 1 1 1 = + R 6 ohm 4 ohm 1 = 3 + 2 R 12 ohm 1 5 = R 12 ohm = 1 5 R = 2, 4 ohm 18

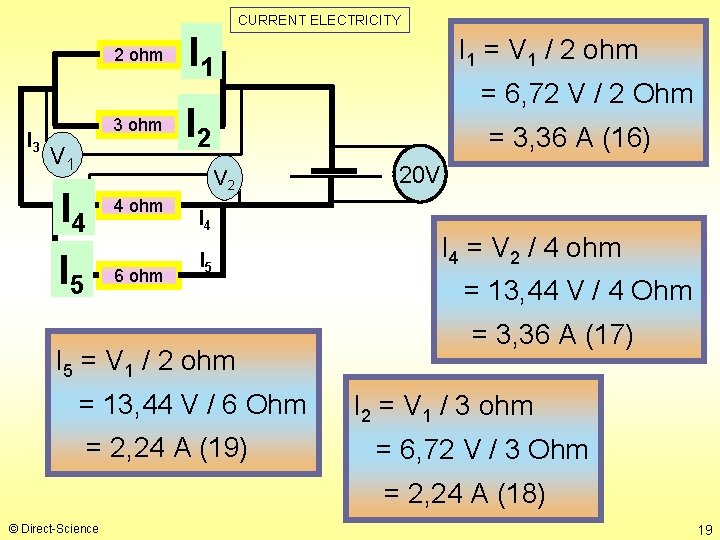
CURRENT ELECTRICITY 2 ohm I 3 3 ohm V 1 I 4 I 5 I 1 6 ohm = 6, 72 V / 2 Ohm I 2 = 3, 36 A (16) V 2 4 ohm I 1 = V 1 / 2 ohm I 4 I 5 = V 1 / 2 ohm = 13, 44 V / 6 Ohm = 2, 24 A (19) 20 V I 4 = V 2 / 4 ohm = 13, 44 V / 4 Ohm = 3, 36 A (17) I 2 = V 1 / 3 ohm = 6, 72 V / 3 Ohm = 2, 24 A (18) © Direct-Science 19

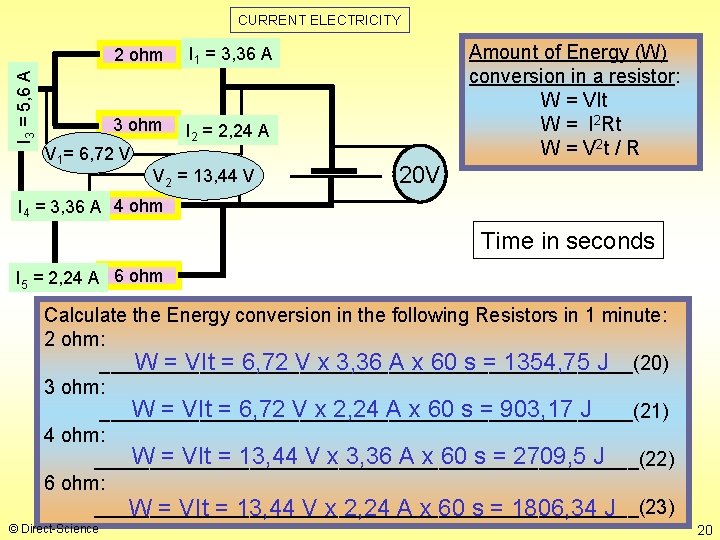
I 3 = 5, 6 A CURRENT ELECTRICITY 2 ohm I 1 = 3, 36 A 3 ohm I 2 = 2, 24 A V 1= 6, 72 V V 2 = 13, 44 V Amount of Energy (W) conversion in a resistor: W = VIt W = I 2 Rt W = V 2 t / R 20 V I 4 = 3, 36 A 4 ohm Time in seconds I 5 = 2, 24 A 6 ohm Calculate the Energy conversion in the following Resistors in 1 minute: 2 ohm: W = VIt = 6, 72 V x 3, 36 A x 60 s = 1354, 75 J ________________________(20) 3 ohm: W = VIt = 6, 72 V x 2, 24 A x 60 s = 903, 17 J ________________________(21) 4 ohm: W = VIt = 13, 44 V x 3, 36 A x 60 s = 2709, 5 J _________________________(22) 6 ohm: _________________________(23) W = VIt = 13, 44 V x 2, 24 A x 60 s = 1806, 34 J © Direct-Science 20

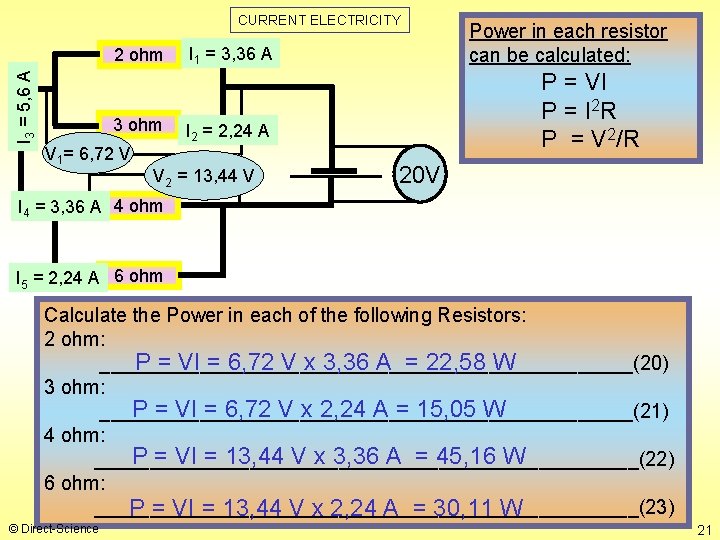
CURRENT ELECTRICITY I 3 = 5, 6 A 2 ohm 3 ohm V 1= 6, 72 V I 1 = 3, 36 A P = VI P = I 2 R P = V 2/R I 2 = 2, 24 A V 2 = 13, 44 V Power in each resistor can be calculated: 20 V I 4 = 3, 36 A 4 ohm I 5 = 2, 24 A 6 ohm Calculate the Power in each of the following Resistors: 2 ohm: P = VI = 6, 72 V x 3, 36 A = 22, 58 W ________________________(20) 3 ohm: P = VI = 6, 72 V x 2, 24 A = 15, 05 W ________________________(21) 4 ohm: P = VI = 13, 44 V x 3, 36 A = 45, 16 W _________________________(22) 6 ohm: _________________________(23) P = VI = 13, 44 V x 2, 24 A = 30, 11 W © Direct-Science 21

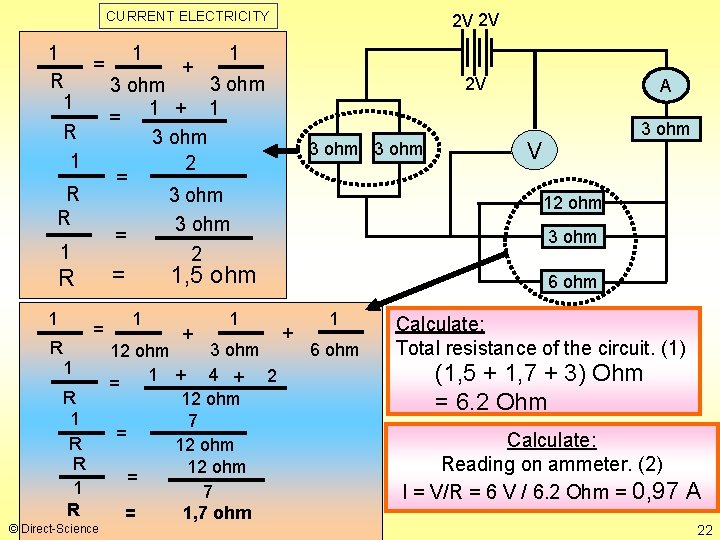
CURRENT ELECTRICITY 2 V 2 V 1 1 1 = + R 3 ohm 1 = 1 + 1 R 3 ohm 1 2 = R 3 ohm = 1 2 = R 1 R © Direct-Science 2 V 3 ohm + 1 3 ohm 12 ohm 1 + 4 + 2 = 12 ohm 7 = 12 ohm = 7 = 1, 7 ohm 3 ohm V 12 ohm 3 ohm 1, 5 ohm 1 A 6 ohm + 1 6 ohm Calculate: Total resistance of the circuit. (1) (1, 5 + 1, 7 + 3) Ohm = 6. 2 Ohm Calculate: Reading on ammeter. (2) I = V/R = 6 V / 6. 2 Ohm = 0, 97 A 22

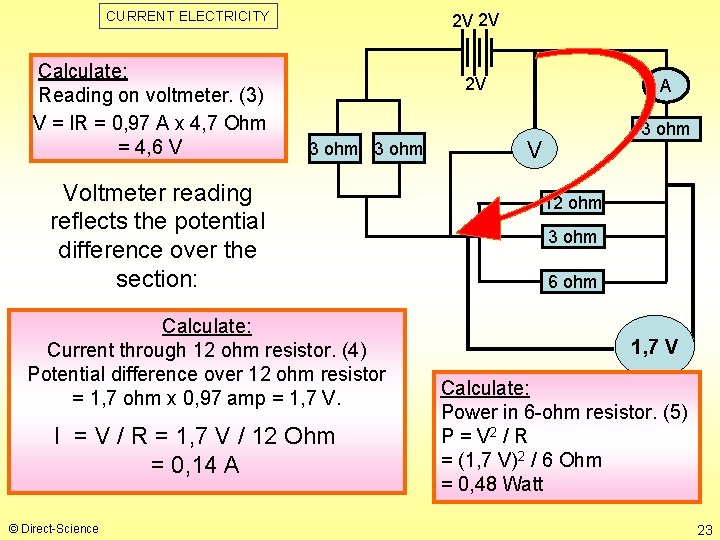
CURRENT ELECTRICITY Calculate: Reading on voltmeter. (3) V = IR = 0, 97 A x 4, 7 Ohm = 4, 6 V 2 V 2 V 2 V 3 ohm Voltmeter reading reflects the potential difference over the section: Calculate: Current through 12 ohm resistor. (4) Potential difference over 12 ohm resistor = 1, 7 ohm x 0, 97 amp = 1, 7 V. I = V / R = 1, 7 V / 12 Ohm = 0, 14 A © Direct-Science A 3 ohm V 12 ohm 3 ohm 6 ohm 1, 7 V Calculate: Power in 6 -ohm resistor. (5) P = V 2 / R = (1, 7 V)2 / 6 Ohm = 0, 48 Watt 23

Direct-Science contact details: Cell: 083 407 8621 Email: vanwykz@yahoo. com Web: www. direct-science. com © Direct-Science