Sample Design for Group Randomized Trials Howard S

Sample Design for Group. Randomized Trials Howard S. Bloom Chief Social Scientist MDRC Prepared for the IES/NCER Summer Research Training Institute held at Northwestern University on July 27, 2010.

Today we will examine Sample size determinants n Precision requirements n Sample allocation n Covariate adjustments n Matching and blocking n Subgroup analyses n Generalizing findings for sites and blocks n Using two-level data for three-level situations n

Part I: The Basics

Statistical properties of grouprandomized impact estimators Unbiased estimates Yij = a+B 0 Tj+ej+eij E(b 0) = B 0 Less precise estimates VAR(eij) = s 2 VAR(ej) = t 2 r = t 2/(t 2+s 2)

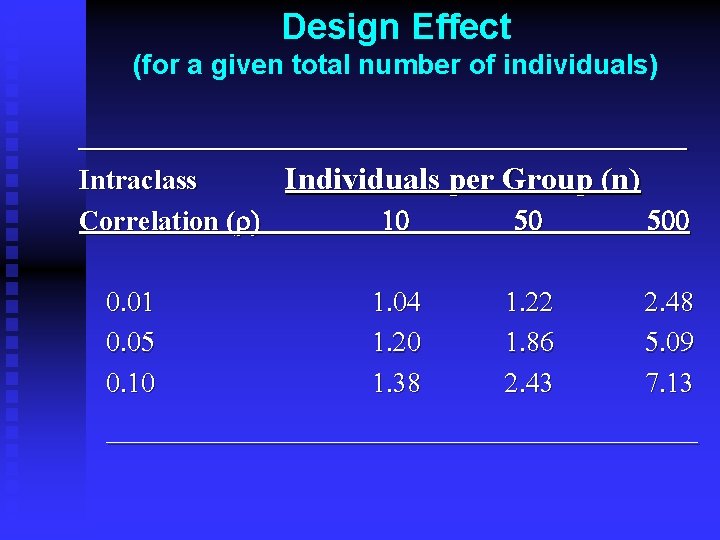
Design Effect (for a given total number of individuals) ___________________ Intraclass Individuals per Group (n) Correlation (r) 0. 01 0. 05 0. 10 10 50 500 1. 04 1. 20 1. 38 1. 22 1. 86 2. 43 2. 48 5. 09 7. 13 ___________________

Sample design parameters n Number of randomized groups (J) n Number of individuals per randomized group (n) n Proportion of groups randomized to program status (P)

Reporting precision n A minimum detectable effect (MDE) is the smallest true effect that has a “good chance” of being found to be statistically significant. n We typically define an MDE as the smallest true effect that has 80 percent power for a two-tailed test of statistical significance at the 0. 05 level. n An MDE is reported in natural units whereas a minimum detectable effect size (MDES) is reported in units of standard deviations

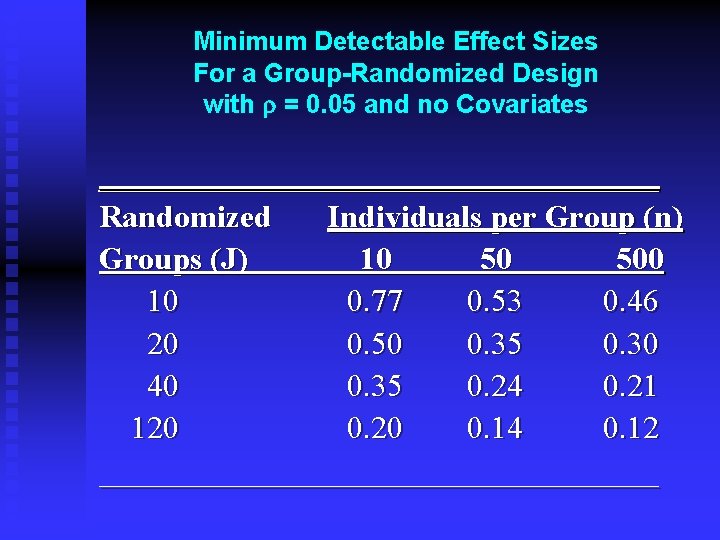
Minimum Detectable Effect Sizes For a Group-Randomized Design with r = 0. 05 and no Covariates __________________ Randomized Individuals per Group (n) Groups (J) 10 50 500 10 0. 77 0. 53 0. 46 20 0. 50 0. 35 0. 30 40 0. 35 0. 24 0. 21 120 0. 14 0. 12 __________________

Implications for sample design n It is extremely important to randomize an adequate number of groups. n It is often far less important how many individuals per group you have.

Part II Determining required precision

When assessing how much precision is needed: Always ask “relative to what? ” Program benefits u Program costs u Existing outcome differences u Past program performance u

Effect Size Gospel According to Cohen and Lipsey Cohen Lipsey (speculative) (empirical) ________________________ Small = Medium = Large = 0. 2 s 0. 5 s 0. 8 s Small = 0. 15 s Medium = 0. 45 s Large = 0. 90 s

Five-year impacts of the Tennessee class-size experiment Treatment: 13 -17 versus 22 -26 students per class Effect sizes: 0. 11 s to 0. 22 s for reading and math Findings are summarized from Nye, Barbara, Larry V. Hedges and Spyros Konstantopoulos (1999) “The Long-Term Effects of Small Classes: A Five. Year Follow-up of the Tennessee Class Size Experiment, ” Educational Evaluation and Policy Analysis, Vol. 21, No. 2: 127 -142.

Annual reading and math growth Reading Math Grade Growth Transition Effect Size --------------------------------K-1 1. 52 1. 14 1 -2 0. 97 1. 03 2 -3 0. 60 0. 89 3 -4 0. 36 0. 52 4 -5 0. 40 0. 56 5 -6 0. 32 0. 41 6 -7 0. 23 0. 30 7 -8 0. 26 0. 32 8 -9 0. 24 0. 22 9 - 10 0. 19 0. 25 10 - 11 0. 19 0. 14 11 - 12 0. 06 0. 01 ------------------------------------------------- Based on work in progress using documentation on the national norming samples for the CAT 5, SAT 9, Terra Nova CTBS, Gates Mac. Ginitie (for reading only), MAT 8, Terra Nova CAT, and SAT 10. 95% confidence intervals range in reading from +/-. 03 to. 15 and in math from +/-. 03 to. 22

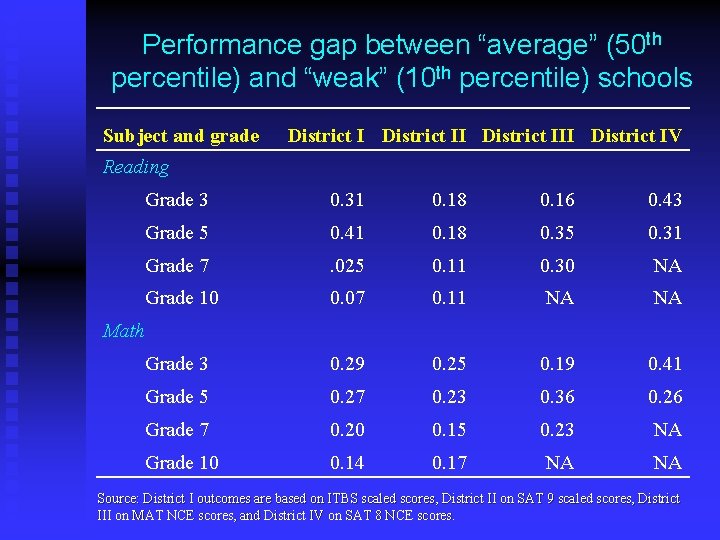
Performance gap between “average” (50 th percentile) and “weak” (10 th percentile) schools Subject and grade District III District IV Reading Grade 3 0. 31 0. 18 0. 16 0. 43 Grade 5 0. 41 0. 18 0. 35 0. 31 Grade 7 . 025 0. 11 0. 30 NA Grade 10 0. 07 0. 11 NA NA Grade 3 0. 29 0. 25 0. 19 0. 41 Grade 5 0. 27 0. 23 0. 36 0. 26 Grade 7 0. 20 0. 15 0. 23 NA Grade 10 0. 14 0. 17 NA NA Math Source: District I outcomes are based on ITBS scaled scores, District II on SAT 9 scaled scores, District III on MAT NCE scores, and District IV on SAT 8 NCE scores.

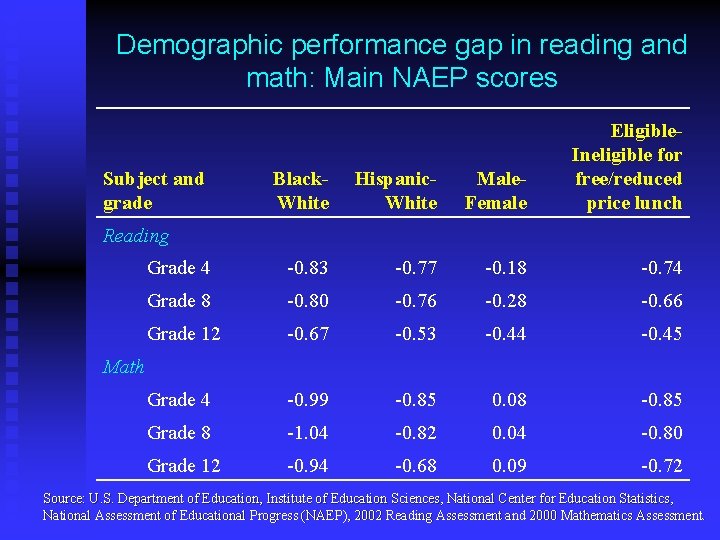
Demographic performance gap in reading and math: Main NAEP scores Black. White Hispanic. White Male. Female Eligible. Ineligible for free/reduced price lunch Grade 4 -0. 83 -0. 77 -0. 18 -0. 74 Grade 8 -0. 80 -0. 76 -0. 28 -0. 66 Grade 12 -0. 67 -0. 53 -0. 44 -0. 45 Grade 4 -0. 99 -0. 85 0. 08 -0. 85 Grade 8 -1. 04 -0. 82 0. 04 -0. 80 Grade 12 -0. 94 -0. 68 0. 09 -0. 72 Subject and grade Reading Math Source: U. S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2002 Reading Assessment and 2000 Mathematics Assessment.

ES Results from Randomized Studies Achievement Measure n Mean 389 0. 33 Standardized test (Broad) 21 0. 07 Standardized test (Narrow) 181 0. 23 Specialized Topic/Test 180 0. 44 Middle Schools 36 0. 51 High Schools 43 0. 27 Elementary School

Part III The ABCs of Sample Allocation

Sample allocation alternatives Balanced allocation maximizes precision for a given sample size; u maximizes robustness to distributional assumptions. u Unbalanced allocation precision erodes slowly with imbalance for a given sample size u imbalance can facilitate a larger sample u Imbalance can facilitate randomization u

Variance relationships for the program and control groups n Equal variances: when the program does not affect the outcome variance. n Unequal variances: when the program does affect the outcome variance.

MDES for equal variances without covariates

How allocation affects MDES

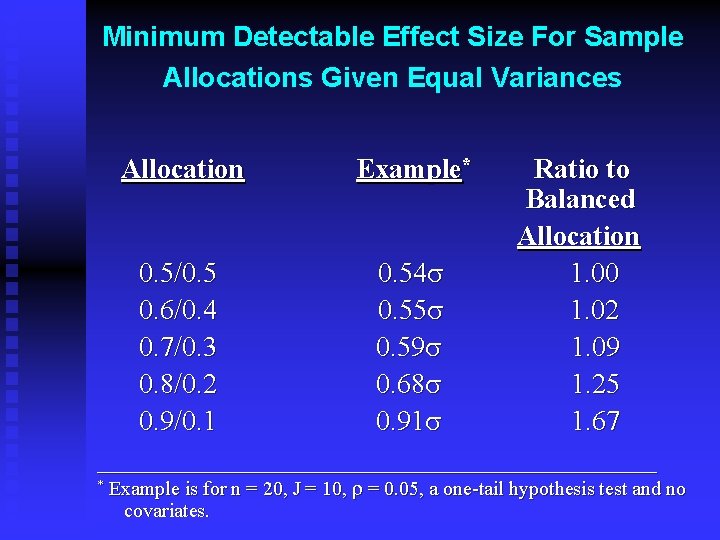
Minimum Detectable Effect Size For Sample Allocations Given Equal Variances Allocation Ratio to Balanced Allocation 0. 5/0. 54 s 1. 00 0. 6/0. 4 0. 55 s 1. 02 0. 7/0. 3 0. 59 s 1. 09 0. 8/0. 2 0. 68 s 1. 25 0. 9/0. 1 0. 91 s 1. 67 ____________________ * Example is for n = 20, J = 10, r = 0. 05, a one-tail hypothesis test and no covariates.

Implications of unbalanced allocations with unequal variances

Implications Continued The estimated standard error is unbiased u u When the allocation is balanced When the variances are equal The estimated standard error is biased upward u When the larger sample has the larger variance The estimated standard error is biased downward u When the larger sample has the smaller variance

Interim Conclusions n Don’t use the equal variance assumption for an unbalanced allocation with many degrees of freedom. n Use a balanced allocation when there are few degrees of freedom.

References Gail, Mitchell H. , Steven D. Mark, Raymond J. Carroll, Sylvan B. Green and David Pee (1996) “On Design Considerations and Randomization-Based Inferences for Community Intervention Trials, ” Statistics in Medicine 15: 1069 – 1092. Bryk, Anthony S. and Stephen W. Raudenbush (1988) “Heterogeneity of Variance in Experimental Studies: A Challenge to Conventional Interpretations, ” Psychological Bulletin, 104(3): 396 – 404.

Part IV Using Covariates to Reduce Sample Size

Basic ideas n Goal: Reduce the number of clusters randomized n Approach: Reduce the standard error of the impact estimator by controlling for baseline covariates n Alternative Covariates u Individual-level u Cluster-level u Pretests u Other characteristics

Impact Estimation with a Covariate yij = the outcome for student i from school j Tj = 1 for treatment schools and 0 for control schools Xj = a covariate for school j xij = a covariate for student i from school j ej = a random error term for school j eij = a random error term for student i from school j

Minimum Detectable Effect Size with a Covariate MDES = minimum detectable effect size MJ-K = a degrees-of-freedom multiplier 1 J = the total number of schools randomized n = the number of students in a grade per school P = the proportion of schools randomized to treatment r = the unconditional intraclass correlation (without a covariate) R 12 = the proportion of variance across individuals within schools (at level 1) predicted by the covariate R 22 = the proportion of variance across schools (at level 2) predicted by the covariate 1 For 20 or more degrees of freedom MJ-K equals 2. 8 for a two-tail test and 2. 5 for a one-tail test with statistical power of 0. 80 and statistical significance of 0. 05

Questions Addressed Empirically about the Predictive Power of Covariates n n n School-level vs. student-level pretests Earlier vs. later follow-up years Reading vs. math Elementary vs. middle vs. high school All schools vs. low-income schools vs. low-performing schools

Empirical Analysis n Estimate r, R 22 and R 12 from data on thousands of students from hundreds of schools, during multiple years at five urban school districts n Summarize these estimates for reading and math in grades 3, 5, 8 and 10 n Compute implications for minimum detectable effect sizes

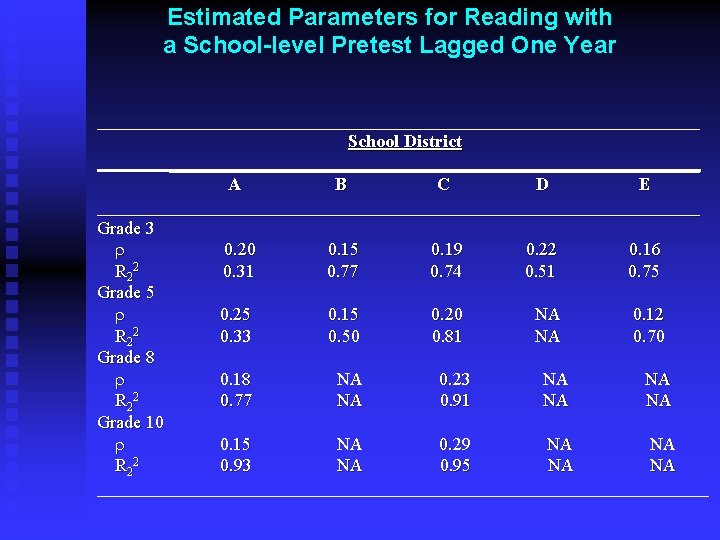
Estimated Parameters for Reading with a School-level Pretest Lagged One Year __________________________________ School District ______________________________ A B C D E __________________________________ Grade 3 r 0. 20 0. 15 0. 19 0. 22 0. 16 R 2 2 0. 31 0. 77 0. 74 0. 51 0. 75 Grade 5 r 0. 25 0. 15 0. 20 NA 0. 12 R 2 2 0. 33 0. 50 0. 81 NA 0. 70 Grade 8 r 0. 18 NA 0. 23 NA NA R 2 2 0. 77 NA 0. 91 NA NA Grade 10 r 0. 15 NA 0. 29 NA NA R 2 2 0. 93 NA 0. 95 NA NA __________________________________

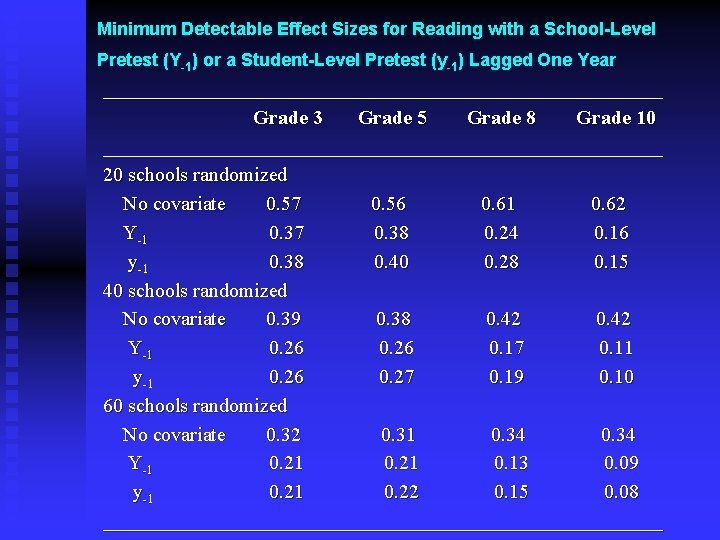
Minimum Detectable Effect Sizes for Reading with a School-Level Pretest (Y-1) or a Student-Level Pretest (y-1) Lagged One Year ____________________________ Grade 3 Grade 5 Grade 8 Grade 10 ____________________________ 20 schools randomized No covariate 0. 57 0. 56 0. 61 0. 62 Y-1 0. 37 0. 38 0. 24 0. 16 y-1 0. 38 0. 40 0. 28 0. 15 40 schools randomized No covariate 0. 39 0. 38 0. 42 Y-1 0. 26 0. 17 0. 11 y-1 0. 26 0. 27 0. 19 0. 10 60 schools randomized No covariate 0. 32 0. 31 0. 34 Y-1 0. 21 0. 13 0. 09 y-1 0. 22 0. 15 0. 08 ____________________________

Key Findings n n n n Using a pretest improves precision dramatically. This improvement increases appreciably from elementary school to middle school to high school because R 22 increases. School-level pretests produce as much precision as do student-level pretests. The effect of a pretest declines somewhat as the time between it and the post-test increases. Adding a second pretest increases precision slightly. Using a pretest for a different subject increases precision substantially. Narrowing the sample to schools that are similar to each other does not improve precision beyond that achieved by a pretest.

Source Bloom, Howard S. , Lashawn Richburg-Hayes and Alison Rebeck Black (2007) “Using Covariates to Improve Precision for Studies that Randomize Schools to Evaluate Educational Interventions” Educational Evaluation and Policy Analysis, 29(1): 30 – 59.

Part V The Putative Power of Pairing A Tail of Two Tradeoffs (“It was the best of techniques. It was the worst of techniques. ” Who the dickens said that? )

Pairing Why match pairs? u for face validity u for precision How to match pairs? u rank order clusters by covariate u pair clusters in rank-ordered list u randomize clusters in each pair

When to pair? n When the gain in predictive power outweighs the loss of degrees of freedom n Degrees of freedom u J - 2 without pairing u J/2 - 1 with pairing

Deriving the Minimum Required Predictive Power of Pairing Without pairing With pairing Breakeven R 2

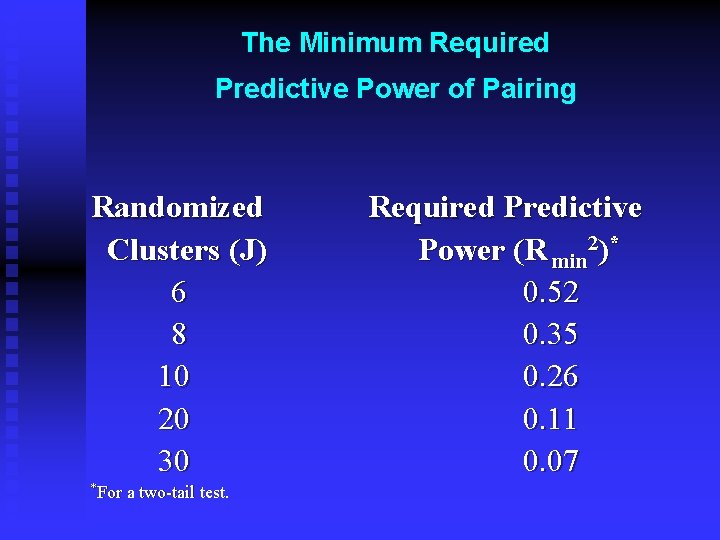
The Minimum Required Predictive Power of Pairing Randomized Clusters (J) 6 8 10 20 30 *For a two-tail test. Required Predictive Power (R min 2)* 0. 52 0. 35 0. 26 0. 11 0. 07

A few key points about blocking Blocking for face validity vs. blocking for precision n Treating blocks as fixed effects vs. random effects n Defining blocks using baseline information n

Part VI Subgroup Analyses #1: When to Emphasize Them

Confirmatory vs. Exploratory Findings n Confirmatory: Draw conclusions about the program’s effectiveness if results are Consistent with theory and contextual factors t Statistically significant and large t And subgroup was pre-specified t n Exploratory: Develop hypotheses for further study 45

Pre-specification Before the analysis, state that conclusions about the program will be based in part on findings for this set of subgroups n Pre-specification can be based on n Theory u Prior evidence u Policy relevance u 46

Statistical significance When should we discuss subgroup findings? n Depends on u Whether significant differences in impacts across subgroups u Might depend on whether impacts for the full sample are statistically significant n 47

Part VII Subgroup Analyses #2: Creating Subgroups

Defining Features n Creating subgroups in terms of: Program characteristics u Randomized group characteristics u Individual characteristics u

Defining Subgroups by Program Characteristics n Based only on program features that were randomized n Thus one cannot use implementation quality

Defining Subgroups by Characteristics Of Randomized Groups n Types of impacts Net impacts u Differential impacts u n Internal validity u n only use pre-existing characteristics Precision Net impact estimates are limited by reduced number of randomized groups u Differential impact estimates are triply limited (and often need four times as many randomized groups) u

Defining Subgroups by Characteristics of Individuals n Types of impacts Net impacts u Differential impacts u n Internal validity Only use pre-existing characteristics u Only use subgroups with sample members from all randomized groups u n Precision For net impacts: can be almost as good as for full sample u For differential impacts: can be even better than for full sample u

Part VIII Generalizing Results from Multiple Sites and Blocks

Fixed vs. Random Effects Inference: A Vexing Issue Known vs. unknown populations u Broader vs. narrower inferences u Weaker vs. stronger precision u Few vs. many sites or blocks u

Weighting Sites and Blocks Implicitly through a pooled regression n Explicitly based on u Number of schools u Number of students n Explicitly based on precision u Fixed effects u Random effects n Bottom line: the question addressed is what counts n

Part IX Using Two-Level Data for Three. Level Situations

The Issue n General Question: What happens when you design a study with randomized groups that comprise three levels based on data which do not account explicitly for the middle level? n Specific Example: What happens when you design a study that randomizes schools (with students clustered in classrooms in schools) based on data for students clustered in schools?

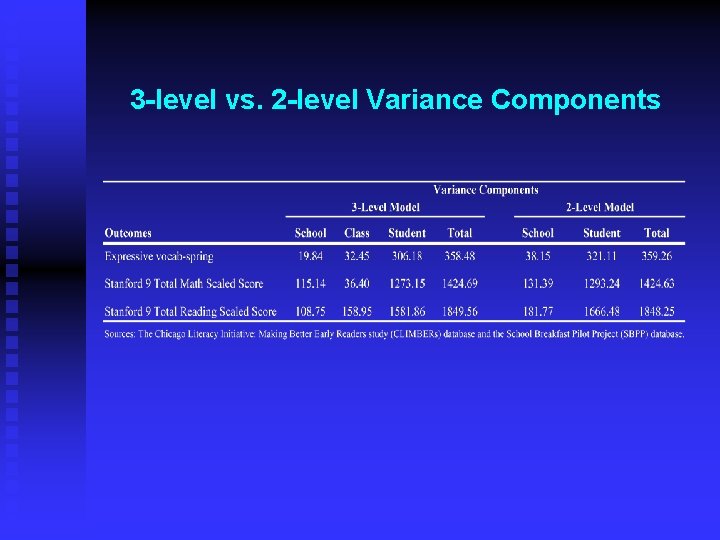
3 -level vs. 2 -level Variance Components

3 -level vs. 2 -level MDES for Original Sample

Further References Bloom, Howard S. (2005) “Randomizing Groups to Evaluate Place-Based Programs, ” in Howard S. Bloom, editor, Learning More From Social Experiments: Evolving Analytic Approaches (New York: Russell Sage Foundation). Bloom, Howard S. , Lashawn Richburg-Hayes and Alison Rebeck Black (2005) “Using Covariates to Improve Precision: Empirical Guidance for Studies that Randomize Schools to Measure the Impacts of Educational Interventions” (New York: MDRC). Donner, Allan and Neil Klar (2000) Cluster Randomization Trials in Health Research (London: Arnold). Hedges, Larry V. and Eric C. Hedberg (2006) “Intraclass Correlation Values for Planning Group Randomized Trials in Education” (Chicago: Northwestern University). Murray, David M. (1998) Design and Analysis of Group-Randomized Trials (New York: Oxford University Press). Raudenbush, Stephen W. , Andres Martinez and Jessaca Spybrook (2005) “Strategies for Improving Precision in Group-Randomized Experiments” (University of Chicago). Raudenbush, Stephen W. (1997) “Statistical Analysis and Optimal Design for Cluster Randomized Trials” Psychological Methods, 2(2): 173 – 185. Schochet, Peter Z. (2005) “Statistical Power for Random Assignment Evaluations of Education Programs, ” (Princeton, NJ: Mathematica Policy Research).