Saluran Transmisi Impedansi dan Admitansi Koridor Penyaluran Energi

Saluran Transmisi Impedansi dan Admitansi

Koridor Penyaluran Energi Saluran transmisi yang akan kita bahas adalah saluran udara, dengan konduktor terbuka yang berarti memenfaatkan udara sebagai bahan isolasi Saluran transmisi merupakan koridor yang harus dilalui dalam penyaluran energi listrik. Walaupun rangkaian ekivalen cukup sederhana, terdapat empat hal yang harus diperhatikan yaitu: § Resistansi konduktor, § Imbas tegangan di satu konduktor oleh arus yang mengalir di konduktor yang lain, § Arus kapasitif karena adanya medan listrik antar konduktor, § Arus bocor pada isolator. biasanya diabaikan karena cukup kecil dibandingkan dengan arus konduktor. Namun arus bocor menjadi sangat penting dalam permasalahan isolator

Sebelum mulai membahas saluran transmisi itu sendiri, perlu kita ingat besaran-besarn fisis udara yang akan masuk dalam perhitungan-perhitungan saluran transmisi, yaitu: Permeabilitas: permeabilitas magnetik udara dianggap sama dengan permeabilitas ruang hampa: Permitivitas: permitivitas elektrik udara dianggap sama dengan permitivitas ruang hampa:

Konduktor

Konduktor Jenis Konduktor Beberapa jenis konduktor: Aluminium: AAL (all aluminium coductor) Aloy aluminium: AAAL (all aluminium alloy conductor) Dengan penguatan kawat baja: ACSR (aluminium conductor steel reinforced) Data mengenai ukuran, konstruksi, resistansi [ per km], radius [cm], GMR [cm] (Geometric Mean Radius) kemampuan mengalirkan arus [A] dapat kita peroleh namun untuk sementara kita tidak membahasnya dalam paparan ini.

Resistansi Seri

Resistansi Seri Resistansi Arus Searah Untuk arus searah, resistansi konduktor diformulasikan: [ ] resistivitas bahan [m. ] panjang konduktor [m] luas penampang [m 2] Resistivitas tergantung dari temperatur.

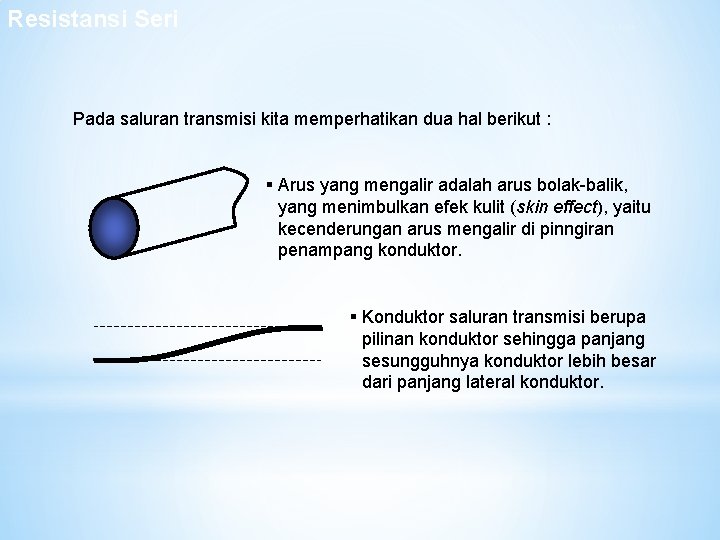
Resistansi Seri Efek Kulit Pada saluran transmisi kita memperhatikan dua hal berikut : § Arus yang mengalir adalah arus bolak-balik, yang menimbulkan efek kulit (skin effect), yaitu kecenderungan arus mengalir di pinngiran penampang konduktor. § Konduktor saluran transmisi berupa pilinan konduktor sehingga panjang sesungguhnya konduktor lebih besar dari panjang lateral konduktor.

Induktansi

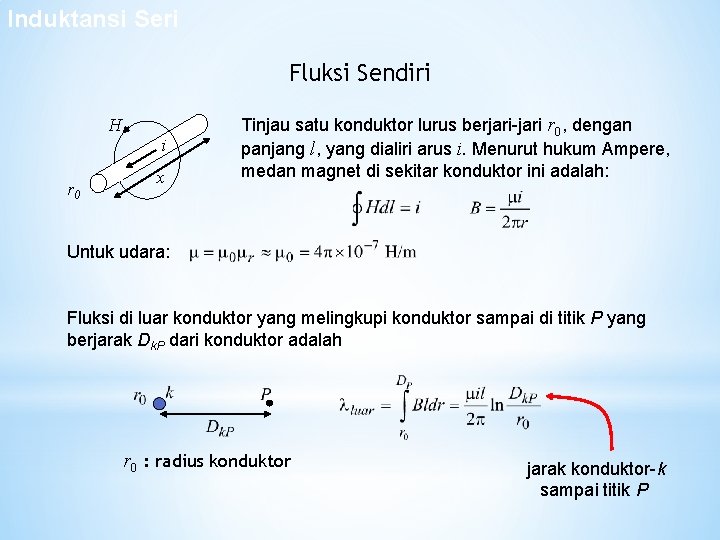
Induktansi Seri Fluksi Sendiri H r 0 i x Tinjau satu konduktor lurus berjari-jari r 0, dengan panjang l, yang dialiri arus i. Menurut hukum Ampere, medan magnet di sekitar konduktor ini adalah: Untuk udara: Fluksi di luar konduktor yang melingkupi konduktor sampai di titik P yang berjarak Dk. P dari konduktor adalah r 0 : radius konduktor jarak konduktor-k sampai titik P

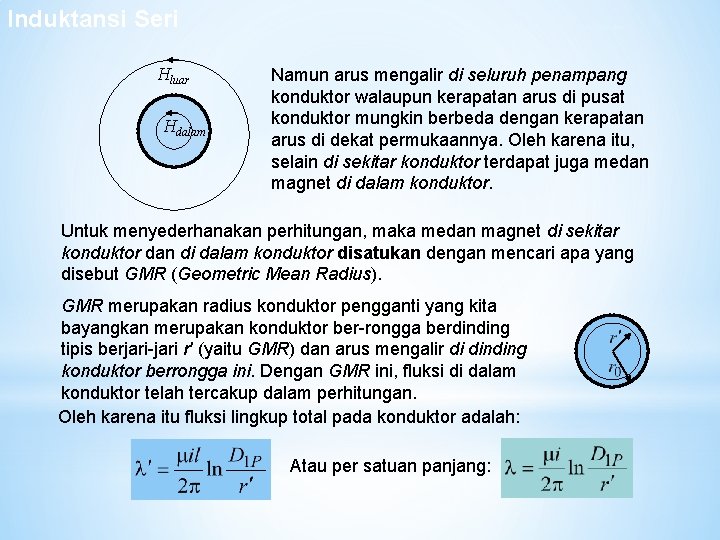
Induktansi Seri Hluar Hdalam Fluksi Sendiri Namun arus mengalir di seluruh penampang konduktor walaupun kerapatan arus di pusat konduktor mungkin berbeda dengan kerapatan arus di dekat permukaannya. Oleh karena itu, selain di sekitar konduktor terdapat juga medan magnet di dalam konduktor. Untuk menyederhanakan perhitungan, maka medan magnet di sekitar konduktor dan di dalam konduktor disatukan dengan mencari apa yang disebut GMR (Geometric Mean Radius). GMR merupakan radius konduktor pengganti yang kita bayangkan merupakan konduktor ber-rongga berdinding tipis berjari-jari r′ (yaitu GMR) dan arus mengalir di dinding konduktor berrongga ini. Dengan GMR ini, fluksi di dalam konduktor telah tercakup dalam perhitungan. Oleh karena itu fluksi lingkup total pada konduktor adalah: Atau per satuan panjang:

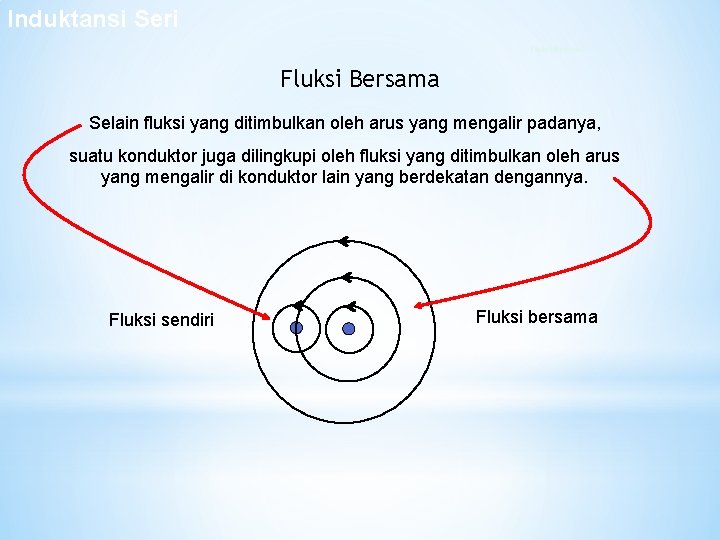
Induktansi Seri Fluksi Bersama Selain fluksi yang ditimbulkan oleh arus yang mengalir padanya, suatu konduktor juga dilingkupi oleh fluksi yang ditimbulkan oleh arus yang mengalir di konduktor lain yang berdekatan dengannya. Fluksi sendiri Fluksi bersama

Induktansi Seri Fluksi Bersama Tinjau satu kelompok n konduktor yang masing-masing dialiri arus ii. Kelompok konduktor ini merupakan satu sistem saluran dengan: Konduktor ke-k memiliki fluksi lingkup total: Fluksi bersama Fluksi sendiri

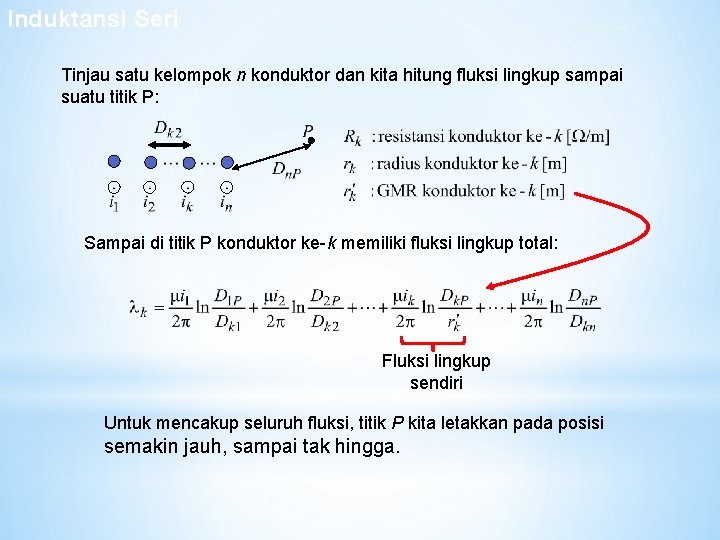
Induktansi Seri Fluksi Bersama Tinjau satu kelompok n konduktor dan kita hitung fluksi lingkup sampai suatu titik P: Sampai di titik P konduktor ke-k memiliki fluksi lingkup total: Fluksi lingkup sendiri Untuk mencakup seluruh fluksi, titik P kita letakkan pada posisi semakin jauh, sampai tak hingga.

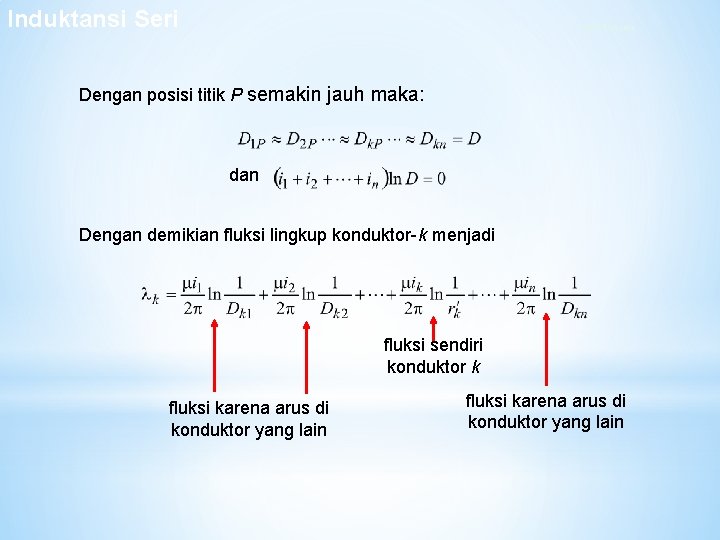
Induktansi Seri Fluksi Bersama Dengan posisi titik P semakin jauh maka: dan Dengan demikian fluksi lingkup konduktor-k menjadi fluksi sendiri konduktor k fluksi karena arus di konduktor yang lain

Induktansi Seri Sistem 4 konduktor Kalau kita batasi tinjauan pada sistem empat konduktor (3 fasa dan 1 netral), relasi fluksi lingkup setiap konduktor adalah:

Impedansi Seri

Impedansi Seri Dengan adanya fluksi lingkup di setiap konduktor maka selain resistansi, setiap konduktor juga mengandung induktansi. Untuk saluran 4 konduktor (3 konduktor fasa dan 1 netral) dengan panjang tertentu kita memiliki rangkaian ekivalen seperti berikut: A B C N RA RB RC RN LAB LBC LCN LAA LBB A′ LAC LCC LNN LAN LBN B′ C′ N′

Impedansi seri A B C N RA RB RC RN LAB LBC LCN LAA LBB A′ LAC LCC LNN LAN LBN Jika konduktor N digunakan sebagai referensi, maka: B′ C′ N′

Impedansi Seri Karena Jadi: maka

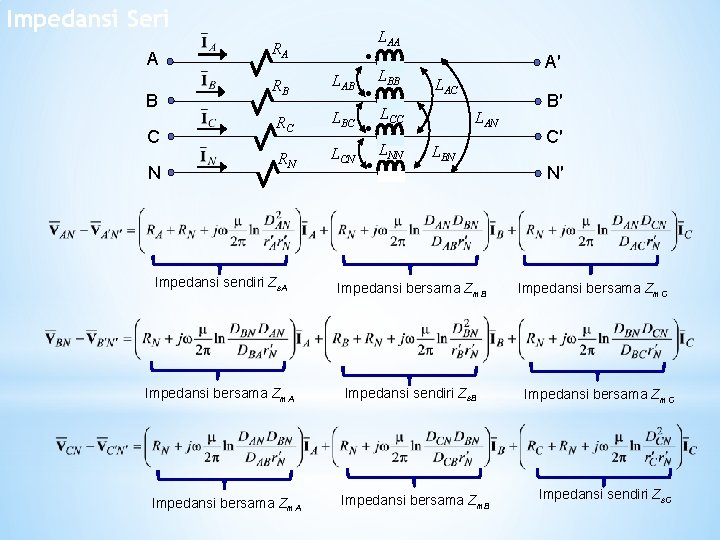
Impedansi Seri A B C N RA RB RC RN LAB LBC LCN LAA LBB A′ LAC LCC LNN LAN LBN Impedansi sendiri Zs. A Impedansi bersama Zm. B Impedansi bersama Zm. A Impedansi sendiri Zs. B Impedansi bersama Zm. A Impedansi bersama Zm. B B′ C′ N′ Impedansi bersama Zm. C Impedansi sendiri Zs. C

Impedansi Seri A B RA RB C N Dalam bentuk matriks Matriks komponen simetris: RC RN LAB LBC LCN LAA LBB A′ LAC LCC LNN LAN LBN B′ C′ N′

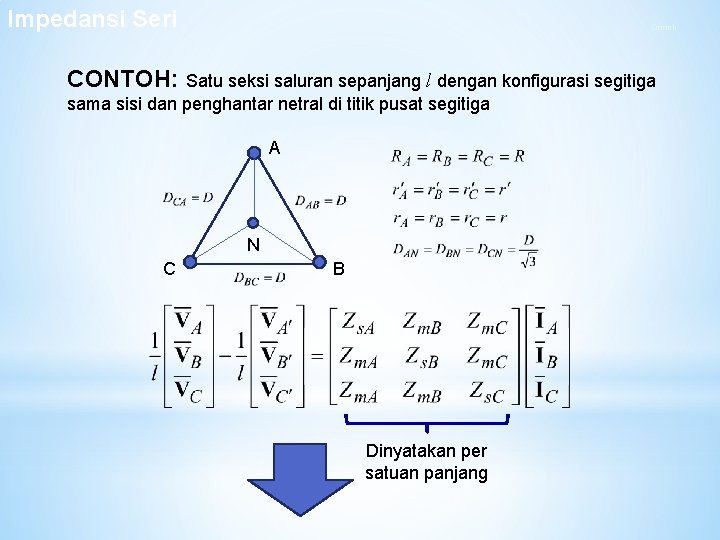
Impedansi Seri Contoh CONTOH: Satu seksi saluran sepanjang l dengan konfigurasi segitiga sama sisi dan penghantar netral di titik pusat segitiga A N C B Dinyatakan per satuan panjang

Impedansi Seri Contoh

Transposisi

Transposisi

Transposisi Jika didefinisikan maka:

Transposisi CONTOH: Tentukan impedansi urutan positif saluran tansmisi: 4, 082 m 230 KV L-L I rated 900 A r = 1, 35 cm r’ = gmr = 1, 073 cm R = 0, 088 / km

Admitansi

Admitansi Jika konduktor lurus kita anggap tak hingga panjangnya dan mengandung muatan dengan kerapatan , maka geometri untuk penerapan hukum Gauss menjadi sederhana. Bidang equipotensial di sekitar konduktor akan berbentuk silindris. Displacement dan kuat medan listrik di suatu titik berjarak x dari konduktor adalah x. B x. A A B Beda potensial antara titik A yang berjarak x. A dari konduktor dan titik B yang berjarak x. B dari konduktor adalah

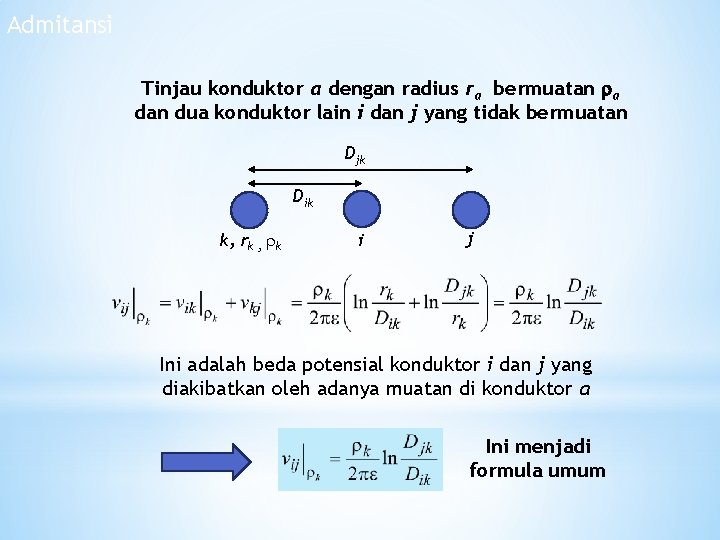
Admitansi Tinjau konduktor a dengan radius ra bermuatan a dan dua konduktor lain i dan j yang tidak bermuatan Djk Dik k, rk , k i j Ini adalah beda potensial konduktor i dan j yang diakibatkan oleh adanya muatan di konduktor a Ini menjadi formula umum

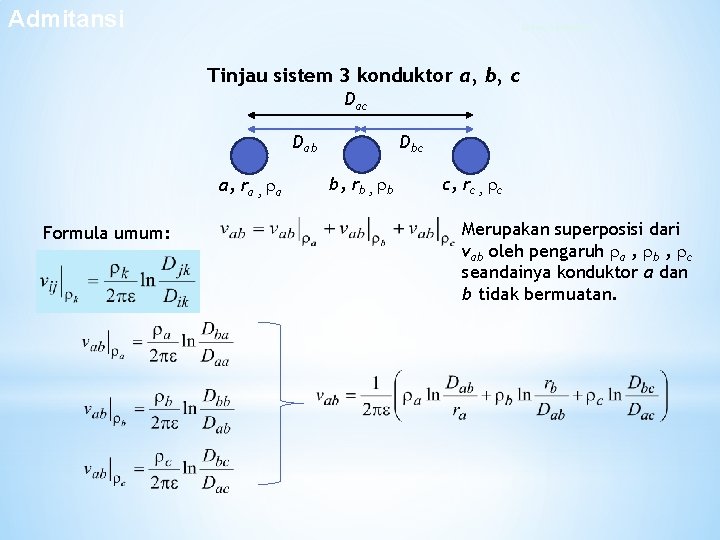
Admitansi Sistem 3 konduktor Tinjau sistem 3 konduktor a, b, c Dab a, ra , a Formula umum: Dbc b, rb , b c, rc , c Merupakan superposisi dari vab oleh pengaruh a , b , c seandainya konduktor a dan b tidak bermuatan.

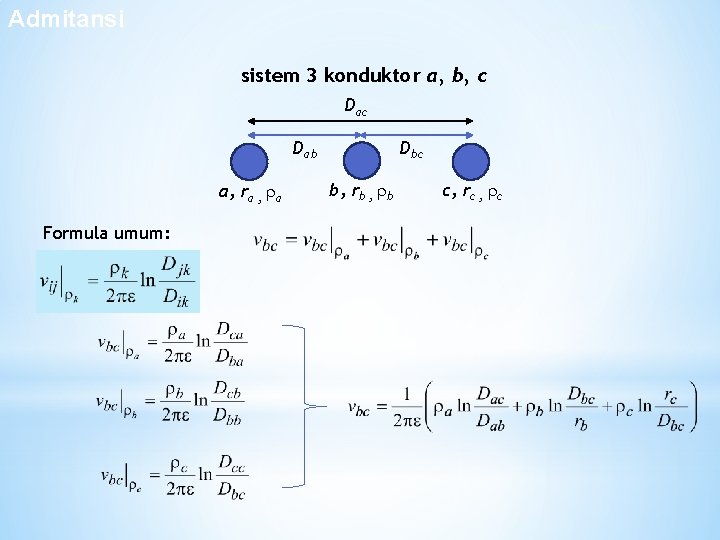
Admitansi Sistem 3 Konduktor sistem 3 konduktor a, b, c Dab a, ra , a Formula umum: Dbc b, rb , b c, rc , c

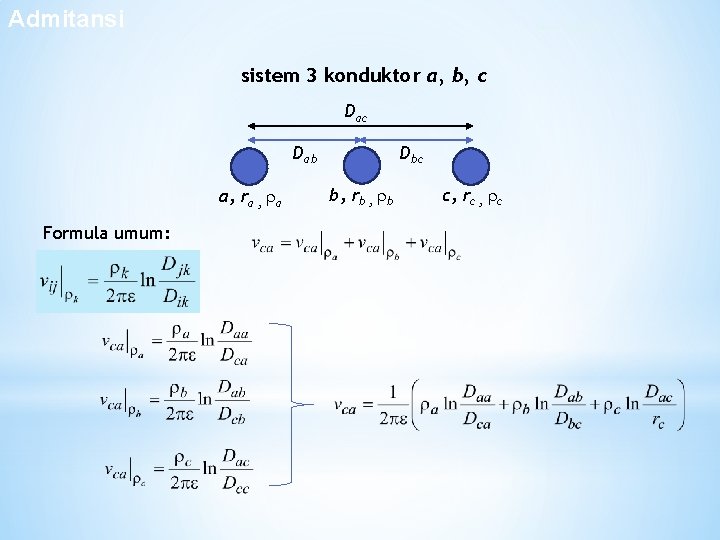
Admitansi Sistem 3 Konduktor sistem 3 konduktor a, b, c Dab a, ra , a Formula umum: Dbc b, rb , b c, rc , c

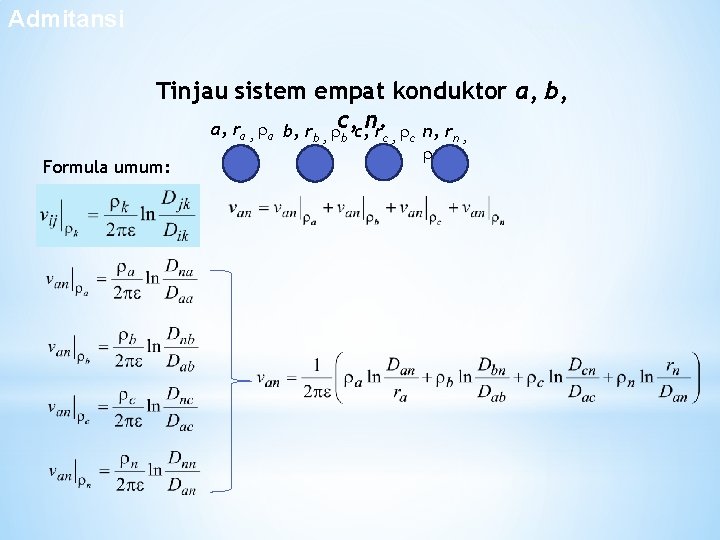
Admitansi Sistem 4 Konduktor Tinjau sistem empat konduktor a, b, a, ra , a b, r c, c, n. r n, r b, Formula umum: b c, c n n,

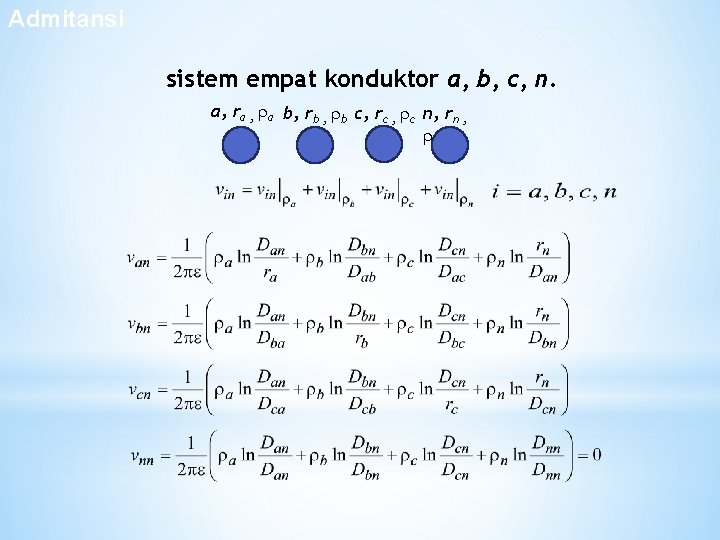
Admitansi Sistem 4 Konduktor sistem empat konduktor a, b, c, n. a, ra , a b, rb , b c, rc , c n, rn , n

Admitansi Sistem 4 Konduktor sistem empat konduktor a, b, c, n. a, ra , a b, rb , b c, rc , c n, rn , n n dapat di-ganti melalui konservasi muatan

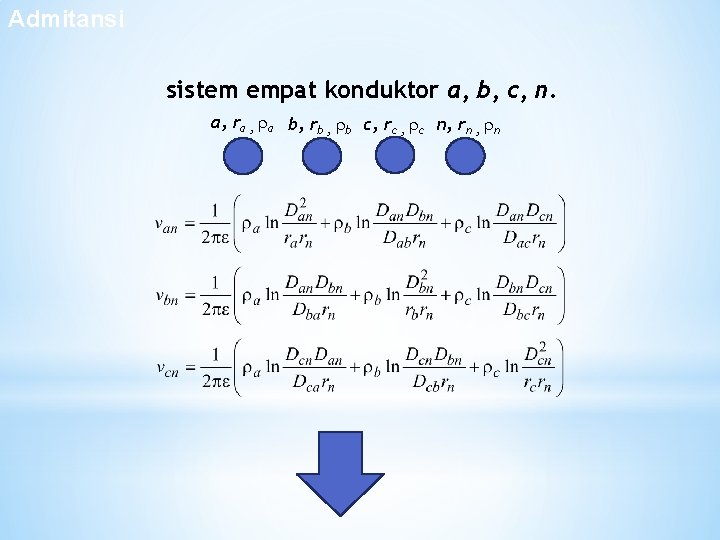
Admitansi Sistem 4 konduktor sistem empat konduktor a, b, c, n. a, ra , a b, rb , b c, rc , c n, rn , n

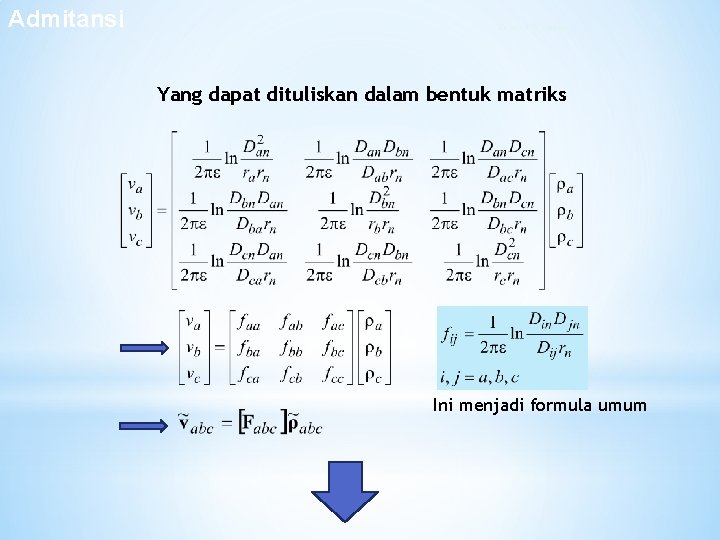
Admitansi Sistem 4 Konduktor Yang dapat dituliskan dalam bentuk matriks Ini menjadi formula umum

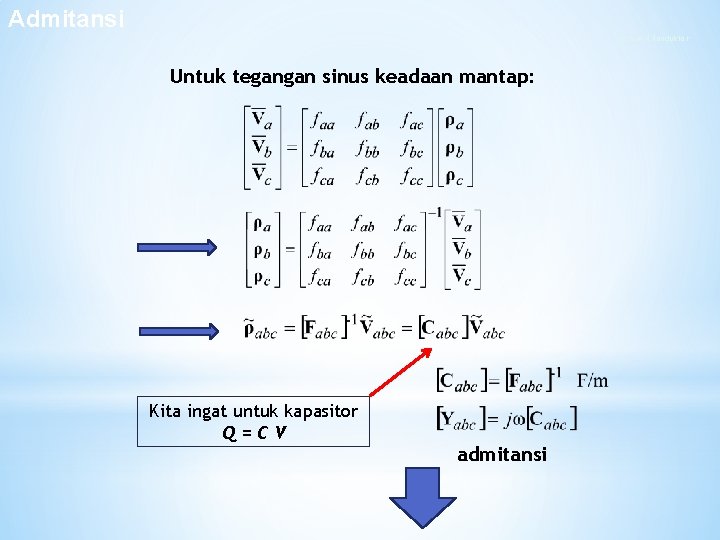
Admitansi Sistem 4 Konduktor Untuk tegangan sinus keadaan mantap: Kita ingat untuk kapasitor Q=CV admitansi

Admitansi Sistem 4 Konduktor Admitansi Inversi matriks ini menyulitkan kita untuk menghitung langsung Yang lebih mudah kita peroleh langsung dari rangkaian adalah Oleh karena itu kita mencari yang akan memberikan

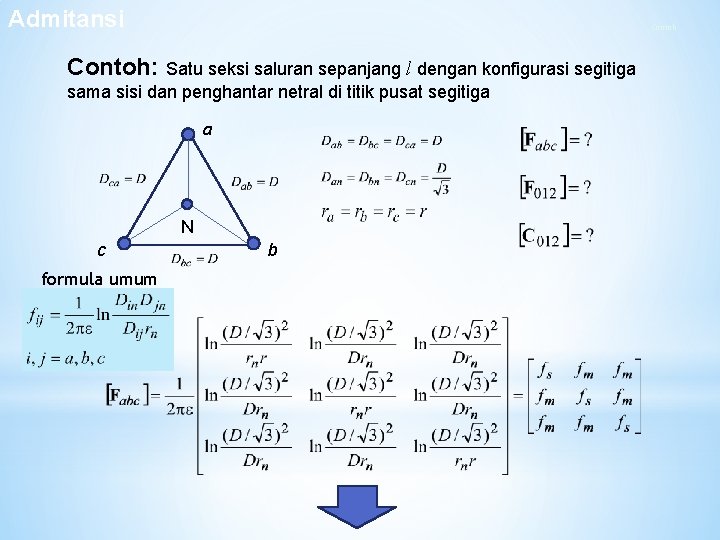
Admitansi Contoh: Satu seksi saluran sepanjang l dengan konfigurasi segitiga sama sisi dan penghantar netral di titik pusat segitiga a N c formula umum b

Admitansi Contoh Kita ingat matriks simetris di mana

Admitansi Contoh yang merupakan matriks simetris dengan mudah memberikan

Transposisi

Transposisi Sistem 4 Konduktor formula umum

Transposisi Sistem 4 Konduktor Telah didefinisikan

Transposisi Contoh: Tentukan admitansi urutan positif Y 1 saluran tansmisi: 4, 082 m 230 KV L-L I rated 900 A r = 1, 35 cm r’ = gmr = 1, 073 cm R = 0, 088 / km

Course Ware Saluran Transmisi Impedansi dan Admitansi Sudaryatno Sudirham