S 1 Representing data Skewness and choice of

S 1 Representing data Skewness and choice of data analysis

Skewness The first distribution shown has a positive skew. This means that it has a long tail in the positive direction. The distribution below it has a negative skew since it has a long tail in the negative direction. Finally, the third distribution is symmetric and has no skew. Distributions with positive skew are sometimes called "skewed to the right" whereas distributions with negative skew are called "skewed to the left. "

Skewness – visuals and calculations Calculate Q 1, Q 2, Q 3, mode, mean and standard deviation Draw all 3 boxplots on one piece of graph paper Data set 1 Data set 2 Data set 3 1, 3, 5, 5, 5, 7, 10 2, 7, 7, 8, 12, 14, 20 3, 6, 7, 9, 10, 11 • For each data set find a relationship between the mode, median and mean using =, >, < symbols • For each data set find a relationship between Q 2 -Q 1 and Q 3 -Q 2 • Work out 3(mean-median) standard deviation

Skewness – Using the Quartiles Q 2 -Q 1 = Q 3 -Q 2 Q 2 -Q 1 < Q 3 -Q 2 Q 2 -Q 1 > Q 3 -Q 2

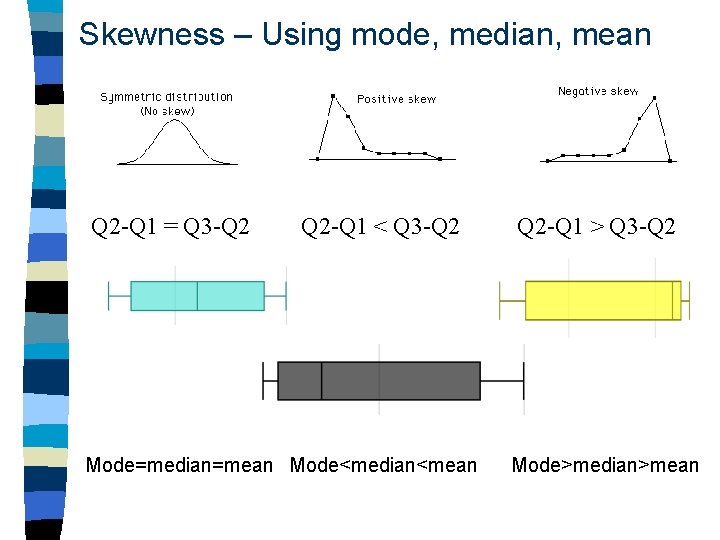
Skewness – Using mode, median, mean Q 2 -Q 1 = Q 3 -Q 2 Q 2 -Q 1 < Q 3 -Q 2 Q 2 -Q 1 > Q 3 -Q 2 Mode=median=mean Mode<median<mean Mode>median>mean

Skewness calculations You can calculate 3(mean-median) Standard deviation This gives you a value to tell you how skewed the data are. The closer the number to zero the more symmetrical the data Negative value means the data has a negative skew and vice versa

Comparing data sets You should always compare data sets using • a measure of location (mean, median, mode) • a measure of spread (range, IQR, standard deviation) • skewness • Range gives a rough idea of spread, but is affected by extreme values. • Generally only used with small data groups • IQR not affected by extreme values • Tells you the spread of middle 50% • Often used in conjunction with median • Mean and standard deviation generally used when data are fairly symmetrical • data size is reasonably large