S 1 PROBABILITY Venn Diagrams and Terminology Venn

S 1 PROBABILITY Venn Diagrams and Terminology

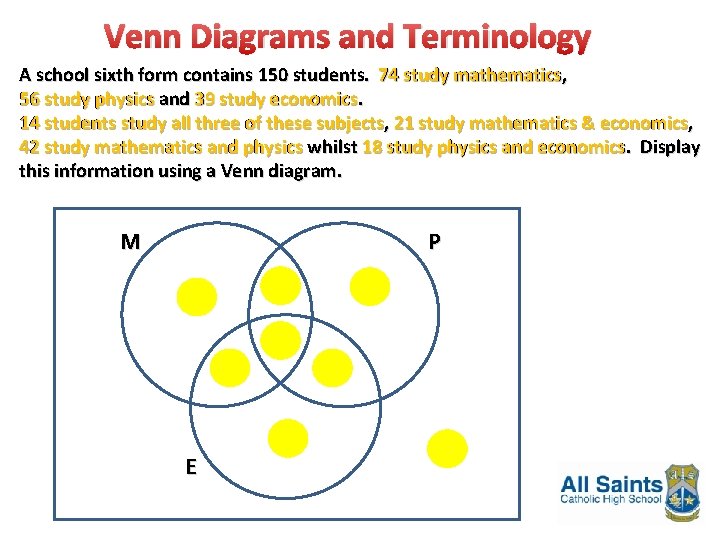
Venn Diagrams and Terminology A school sixth form contains 150 students. 74 study mathematics, 56 study physics and 39 study economics 14 students study all three of these subjects, subjects 21 study mathematics & economics, 42 study mathematics and physics whilst 18 study physics and economics. Display this information using a Venn diagram. M P 28 25 7 E 14 14 10 4 48

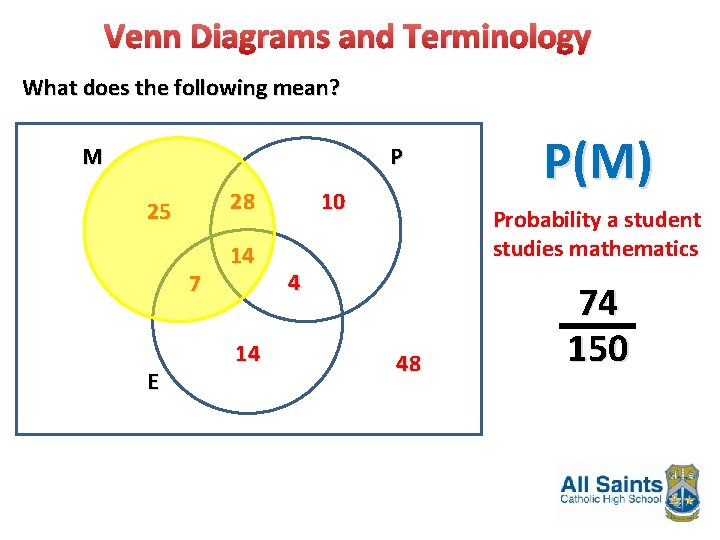
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 P(M) Probability a student studies mathematics 4 48 74 150

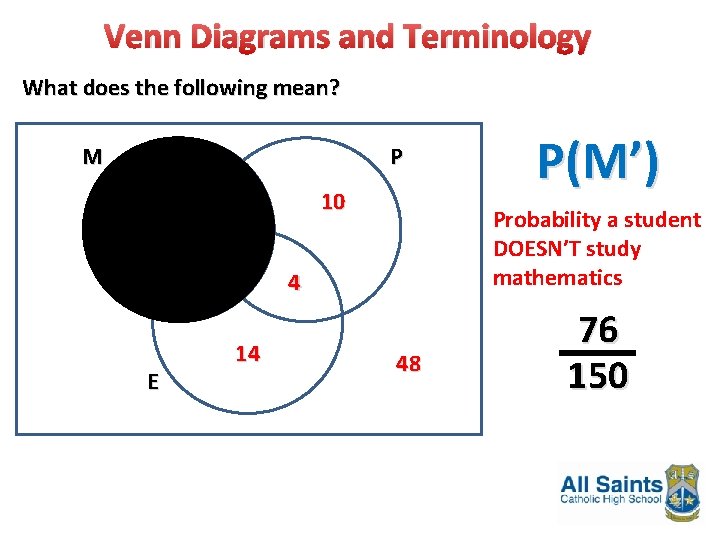
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 P(M’) Probability a student DOESN’T study mathematics 4 48 76 150

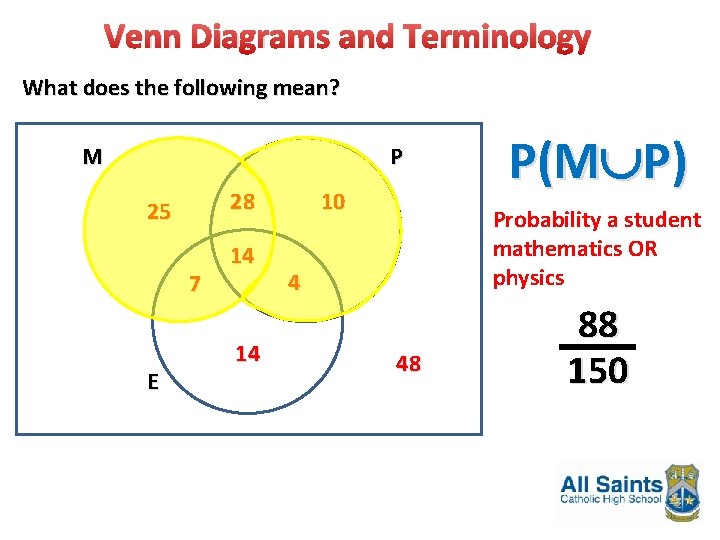
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 P(M P) Probability a student mathematics OR physics 4 48 88 150

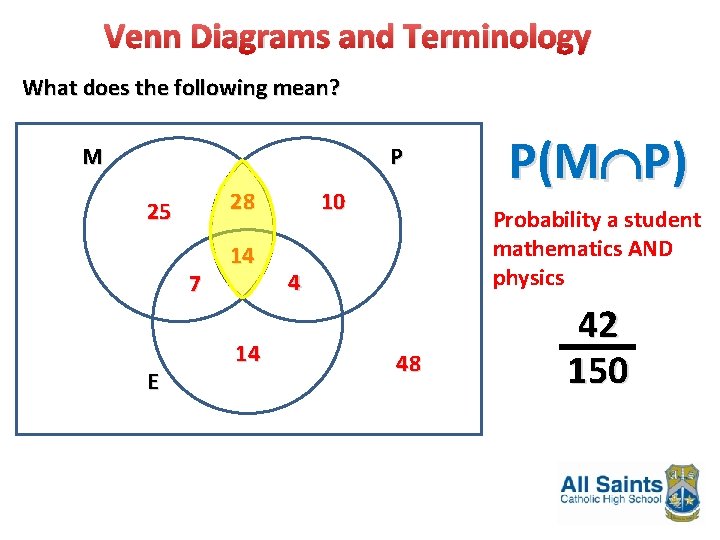
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 P(M P) Probability a student mathematics AND physics 4 48 42 150

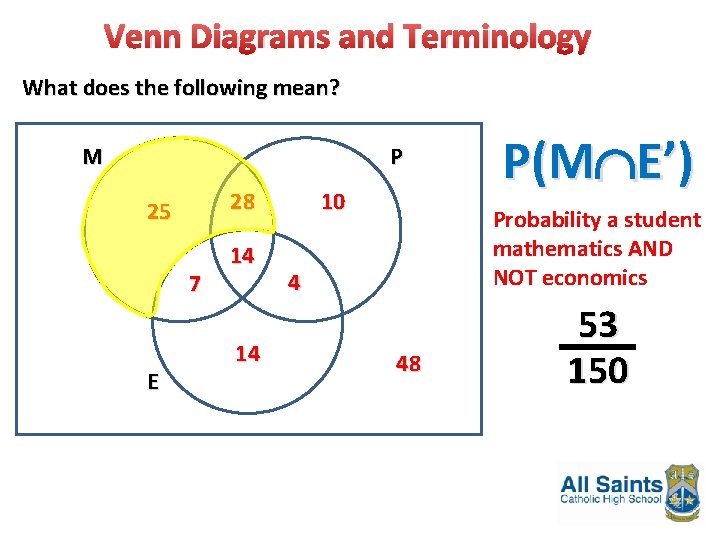
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 P(M E’) Probability a student mathematics AND NOT economics 4 48 53 150

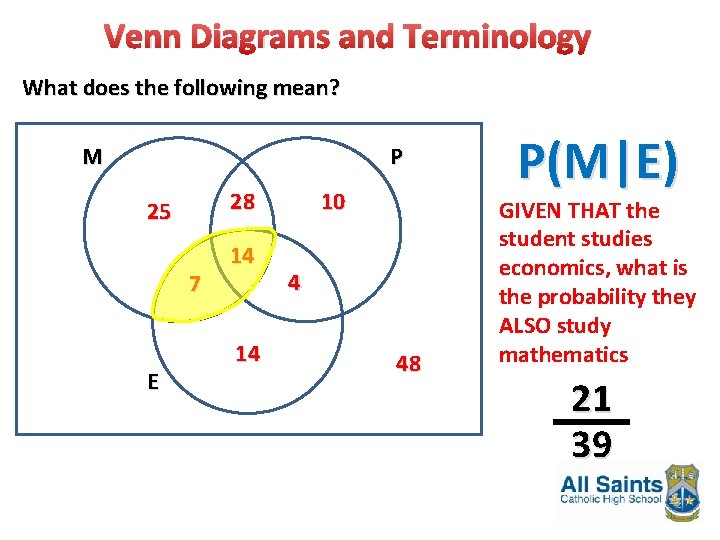
Venn Diagrams and Terminology What does the following mean? M P 28 25 7 E 14 14 10 4 48 P(M|E) GIVEN THAT the student studies economics, what is the probability they ALSO study mathematics 21 39

A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. (a) Draw a Venn diagram to represent these data. (6) One of the adults is then selected at random. Find the probability that she reads (b) at least one of the newspapers, (2) (c) only A, (1) (d) only one of the newspapers, (2) (e) A given that she reads only one newspaper. (2)

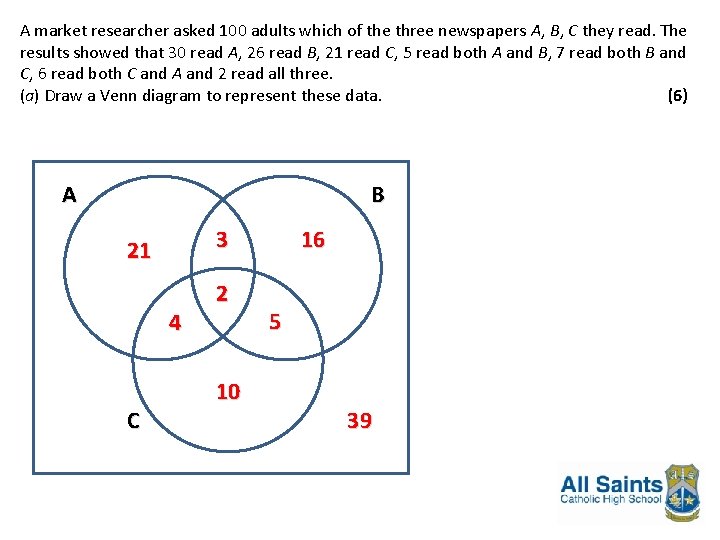
A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. (a) Draw a Venn diagram to represent these data. (6) A B 3 21 4 C 2 10 16 5 39

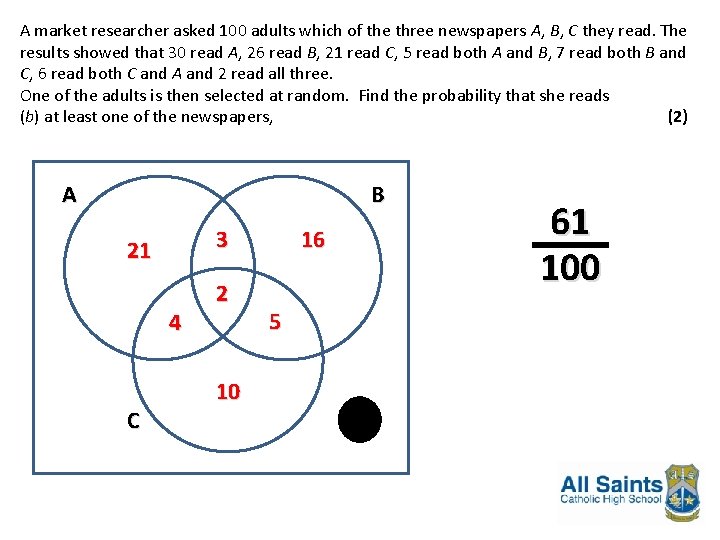
A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. One of the adults is then selected at random. Find the probability that she reads (b) at least one of the newspapers, (2) A B 3 21 4 C 2 10 16 5 39 61 100

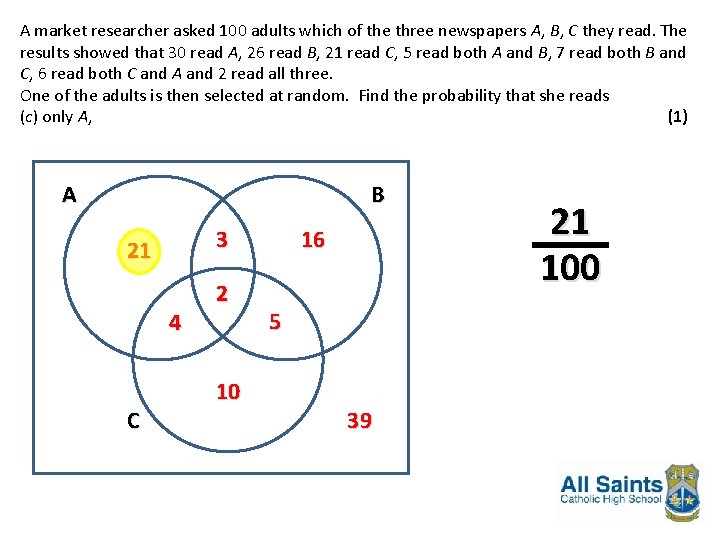
A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. One of the adults is then selected at random. Find the probability that she reads (c) only A, (1) A B 3 21 4 C 2 10 16 5 39 21 100

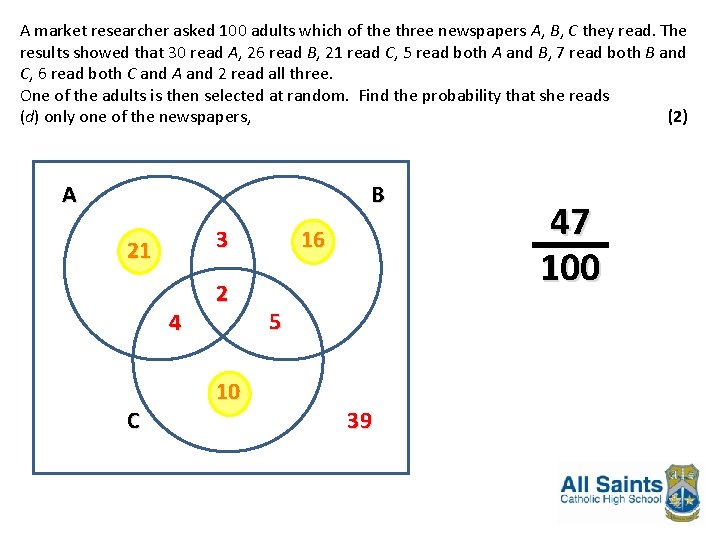
A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. One of the adults is then selected at random. Find the probability that she reads (d) only one of the newspapers, (2) A B 3 21 4 C 2 10 16 5 39 47 100

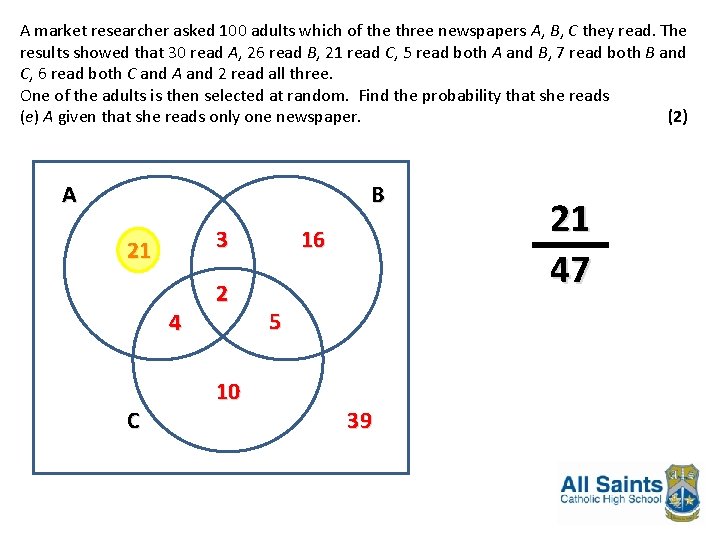
A market researcher asked 100 adults which of the three newspapers A, B, C they read. The results showed that 30 read A, 26 read B, 21 read C, 5 read both A and B, 7 read both B and C, 6 read both C and A and 2 read all three. One of the adults is then selected at random. Find the probability that she reads (e) A given that she reads only one newspaper. (2) A B 3 21 4 C 2 10 16 5 39 21 47