Ryan ODonnell CMU Yi Wu CMU IBM Yuan

Ryan O'Donnell (CMU) Yi Wu (CMU, IBM) Yuan Zhou (CMU)

Locality Sensitive Hashing h: H: [Indyk-Motwani '98] objects sketches family of hash functions h s. t. “similar” objects collide w/ high prob. “dissimilar” objects collide w/ low prob.

Abbreviated history

B dd d 3 ? ? [Broder '98] wo r d 2 wo r A d 1 ? ? Min-wise hash functions 0 1 1 1 0 0 0 1 Jaccard similarity: Invented simple H s. t. Pr [h(A) = h(B)] =

Indyk-Motwani '98 Defined LSH. Invented very simple H good for {0, 1}d under Hamming distance. Showed good LSH implies good nearest-neighbor-search data structs.

Charikar '02, STOC Proposed alternate H (“simhash”) for Jaccard similarity. Patented by Google .

Many papers about LSH

Practice Theory Free code base [AI’ 04] [Broder ’ 97] Sequence comparison in bioinformatics [Indyk–Motwani ’ 98] Association-rule finding in data mining [Gionis–Indyk–Motwani ’ 98] [Charikar ’ 02] [Datar–Immorlica– –Indyk–Mirrokni ’ 04] Collaborative filtering [Motwani–Naor–Panigrahi ’ 06] Clustering nouns by meaning in NLP [Andoni–Indyk ’ 06] [Tenesawa–Tanaka ’ 07] Pose estimation in vision [Andoni–Indyk ’ 08, CACM] • • • [Neylon ’ 10]

Given: Goal: (X, dist), r > 0, distance space “radius” c>1 “approx factor” Family H of functions X → S (S can be any finite set) s. t. ∀ x, y ∈ X, ≤r . 25. 5 ≥q pρ. 1 ≥ cr ≤q

Theorem [IM’ 98, GIM’ 98] Given LSH family for (X, dist), can solve “(r, cr)-near-neighbor search” for n points with data structure of size: query time: O(n 1+ρ) Õ(nρ) hash fcn evals.

Example X = {0, 1}d, dist = Hamming r = εd, c=5 0 1 1 1 0 0 0 1 [IM’ 98] H= { h 1, h 2, …, hd }, hi(x) = xi “output a random coord. ” dist ≤ εd or ≥ 5εd

Optimal upper bound ( {0, 1}d, Ham ), S ≝ {0, 1}d ∪ {✔}, hab(x) = r > 0, c > 1. H ≝ {hab : dist(a, b) ≤ r} ✔ x if x = a or x = b otherwise ≤r . 1. 5 positive. 01 => 0. 0001 ≥ cr = 0

The End. Any questions?

Wait, what? Theorem [IM’ 98, GIM’ 98] Given LSH family for (X, dist), can solve “(r, cr)-near-neighbor search” for n points with data structure of size: query time: O(n 1+ρ) Õ(nρ) hash fcn evals.

Wait, what? Theorem [IM’ 98, GIM’ 98] Given LSH family for (X, dist), can solve “(r, cr)-near-neighbor search” for n points with data structure of size: query time: O(n 1+ρ) Õ(nρ) hash fcn evals. q ≥ n-o(1) ("not tiny")

More results For Rd with ℓp-distance: when p = 1, 0 < p < 1, p = 2 [IM’ 98] [DIIM’ 04] [AI’ 06] For Jaccard similarity: ρ ≤ 1/c [Bro’ 98] For {0, 1}d with Hamming distance: [MNP’ 06] immediately −od(1) (assuming q ≥ 2−o(d)) for ℓp-distance

Our Theorem For {0, 1}d with Hamming distance: (∃ r s. t. ) immediately −od(1) (assuming q ≥ 2−o(d)) for ℓp-distance Proof also yields ρ ≥ 1/c for Jaccard.

Proof

Proof: Noise-stability is log-convex.

Proof: A definition, and two lemmas.

Definition: Noise stability at -т e Fix any arbitrary function h : {0, 1}d → S. Pick x ∈ {0, 1}d at random: x= 0 1 1 1 0 0 h(x) = s Flip each bit w. p. (1 -e-2 т)/2 independenttly y= 0 def: 0 1 1 0 h(y) = s’

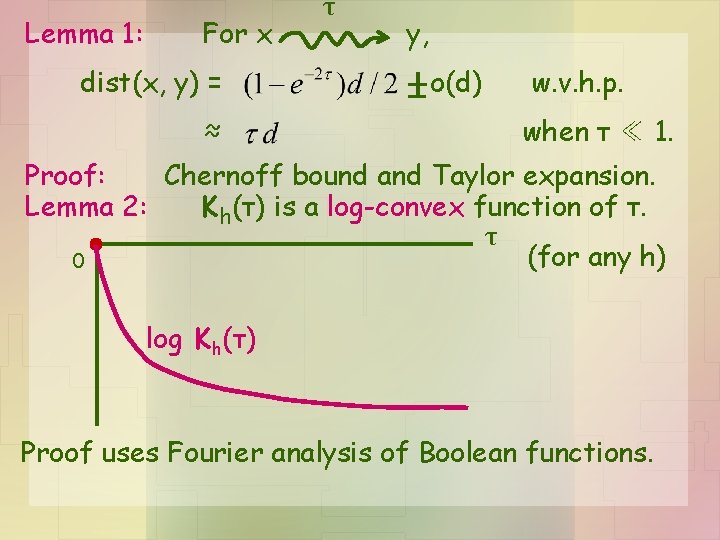
Lemma 1: For x dist(x, y) = ≈ τ y, o(d) w. v. h. p. when τ ≪ 1. Proof: Chernoff bound and Taylor expansion. Lemma 2: Kh(τ) is a log-convex function of τ. τ (for any h) 0 log Kh(τ) Proof uses Fourier analysis of Boolean functions.

Fourier transformation • Theorem. f : {0, 1}d -> R can be uniquely written as Fourier Basis coef. fcns. where • Proof. {0, 1}d -> R}. is an orthonormal basis of {f :

Lemma 2: Kh(τ) is a log-convex function of τ. Proof: Let hi(x) = 1 h(x)=i.

Lemma 2: Kh(τ) is a log-convex function of τ. Proof: Let hi(x) = 1 h(x)=i. non-neg comb. of log-convex fcns.

Lemma 1: For x dist(x, y) = τ y, o(d) ≈ Lemma 2: 0 w. v. h. p. when τ ≪ 1. Kh(τ) is a log-convex function of τ. τ (for any h) log Kh(τ) Theorem: LSH for {0, 1}d requires .

Proof: Say H is an LSH family for {0, 1}d with params (εd + o(d), cεd - o(d), r (c − o(1)) r qρ, q). ( Non-neg. lin. comb. Θ(d) ; we assume q not tiny − of log-convex fcns. in truth, q+2 def: ∴ KH(τ) is also log-convex. ) w. v. h. p. , dist(x, y) ≈ (1 - e-т)d ≈ тd ∴ KH(ε) ≳ qρ KH(cε) ≲ q

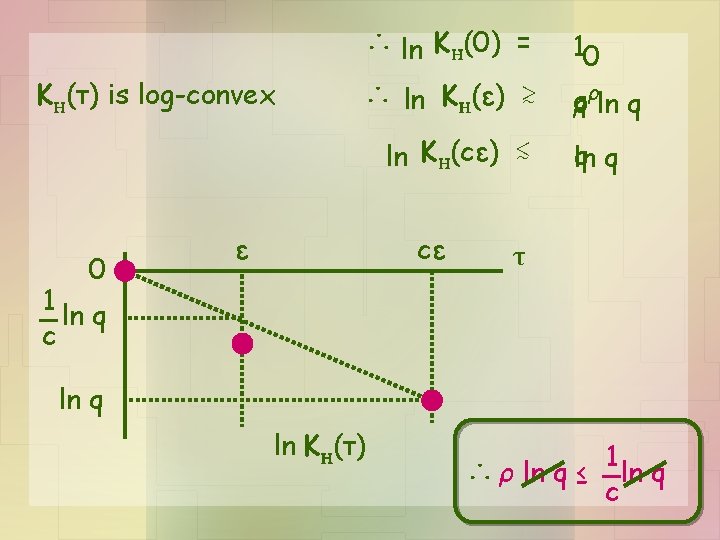
∴ ln KH(0) = KH(τ) is log-convex ∴ ln KH(ε) ≳ ln KH(cε) ≲ 0 ε cε 10 ρ q ρ ln q q q ln τ 1 ln q c ln q ln KH(τ) 1 ∴ ρ ln q ≤ ln q c

The End. Any questions?