rvores de Sufixo Jeane Ceclia Roteiro n n

Árvores de Sufixo Jeane Cecília

Roteiro n n n Definição Aplicações Construção n n n Algoritmo de Mc. Creight Exemplo Outros Algoritmos

Árvores de Sufixo n Estrutura de dados que permite a representação de todos os sufixos de um determinado string S. n Pode ser construída em tempo O(|S|). n Permite a localização de um padrão p em tempo O(|p|).

Árvore de Sufixo n Árvore enraizada, com n folhas. n Cada aresta é rotulada por um substring de S. n Arestas que saem de um vértice devem ter rótulos com prefixos diferentes. n Cada folha corresponde a um sufixo de S.

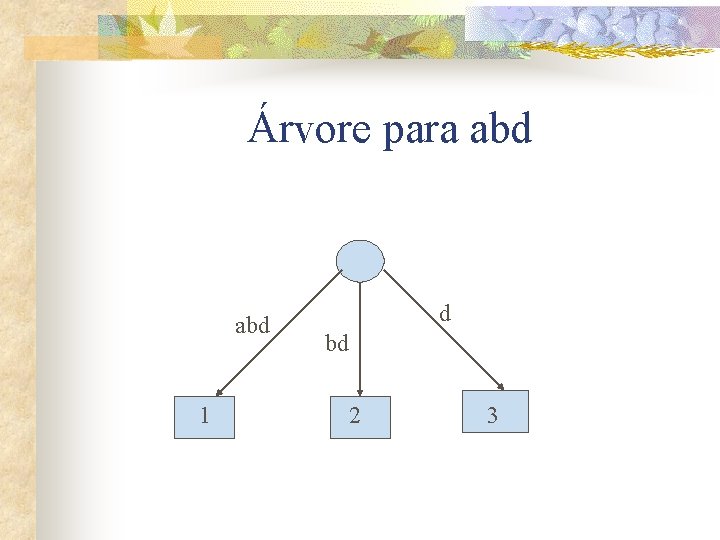
Árvore para abd 1 d bd 2 3

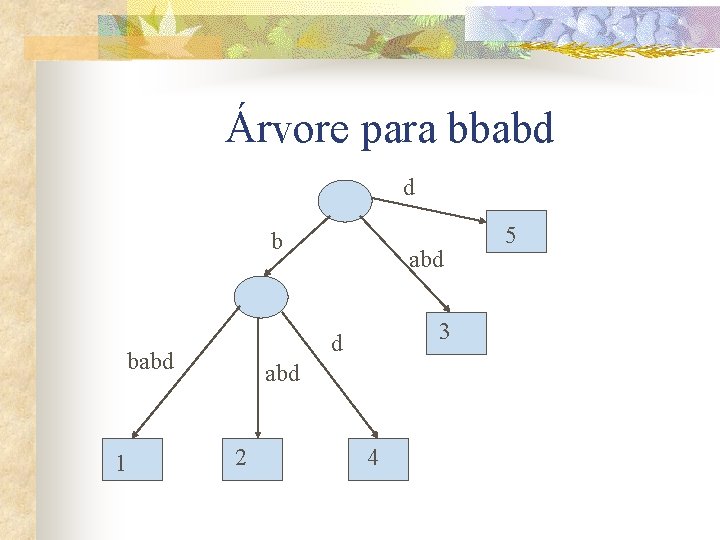
Árvore para bbabd d b 3 d babd 1 abd 2 4 5

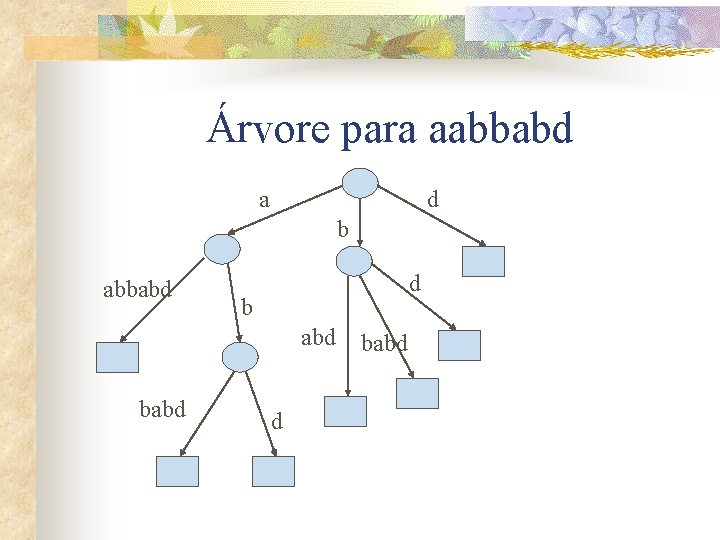
Árvore para aabbabd a d b abbabd d b abd babd

Aplicações de Árvore de Sufixo n Encontrar todas as ocorrências de um padrão (sequenciamento de DNA em Larga escala). n Encontrar todas os substrings que contém um padrão (localização de primers). n Encontrar o maior substring comum aos strings S e T (tempo O(|S| + |T|).

Construção de Árvores de Sufixo n Algoritmo de Mc. Creight n Mapeamento de um string finito S em uma árvore T. n Caminhos em T são sufixos de S. n Nós terminais de T são posições de S. n Tempo: O(n log| |)

Algoritmo de Mc. Creight n Restrições n Uma aresta de T pode representar qualquer substring não vazio de S. n Cada nó não terminal de T deve ter pelo menos dois filhos (exceto a raiz). n O caractere final de S não pode aparecer em outra parte deste.

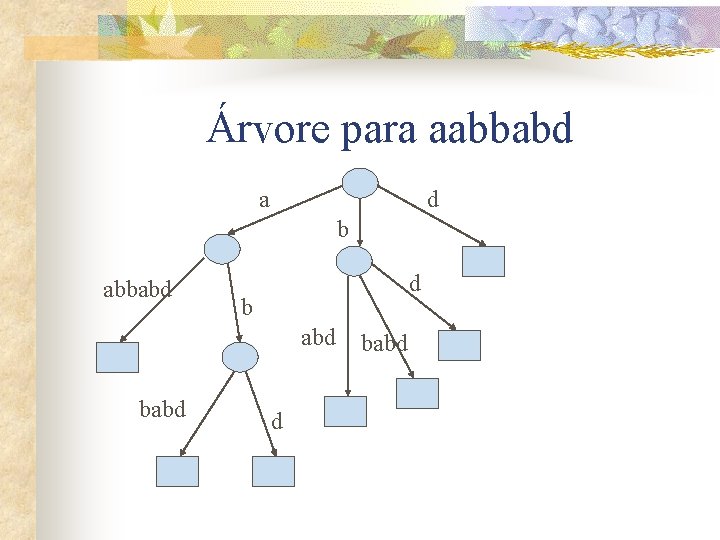
Árvore para aabbabd a d b abbabd d b abd babd

Definições n Caminho parcial n n Caminho n n Qualquer caminho a partir da raiz Caminho parcial que finaliza em um nó terminal Locus n Nó final de um caminho parcial

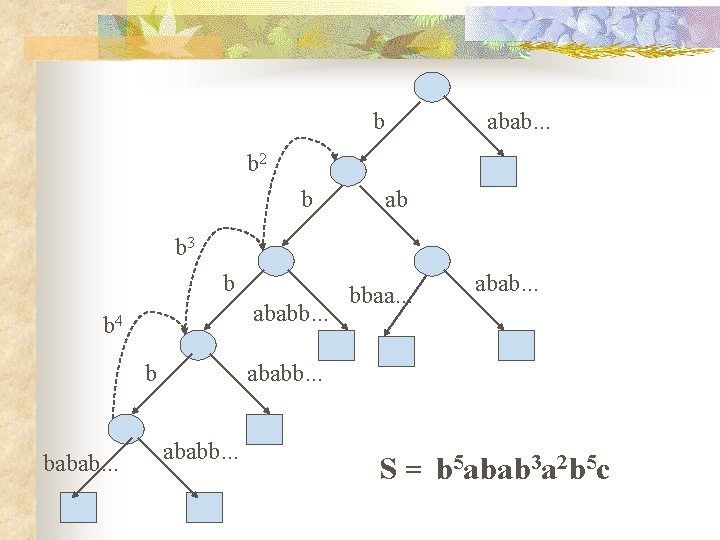
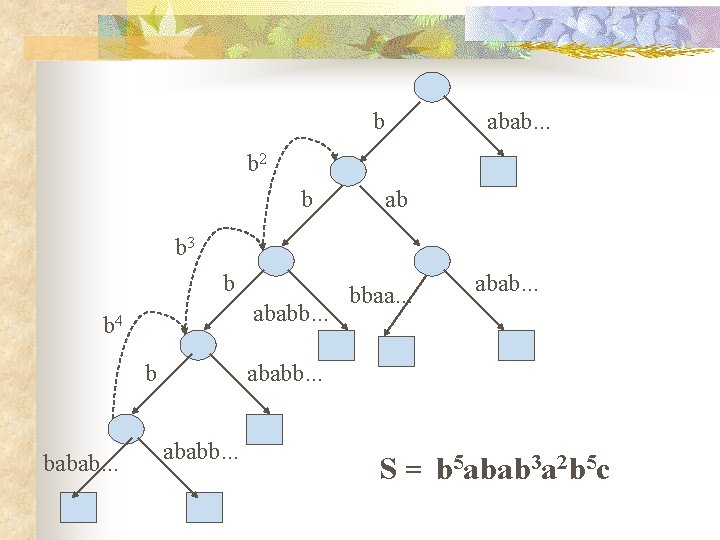
b abab. . . b 2 b ab b 3 b ababb. . . b 4 b babab. . . bbaa. . . ababb. . . S = b 5 abab 3 a 2 b 5 c

Definições = abbab n Extensão de n n Locus estendido de n n Qualquer string do qual é um prefixo: abbab****** Locus (definido) da menor extensão de Locus contraído de n Locus (definido) do maior prefixo de

Definições attgacgattc n n n head 7 = ga suf 7 = gattc tail 7 = ttc suf i : sufixo de S. head i : maior prefixo de sufi que também é prefixo de sufj (j<i). tail i = sufi-headi

Idéia Geral do Algoritmo n n No passo i é inserido o sufi na árvore Ti-1, obtendo a árvore Ti. Procedimento n n n Localiza o locus estendido de headi em Ti-1. Constrói um novo nó terminal para ser o locus de headi (caso este não exista) Acrescenta uma aresta rotulada taili, ligando o locus de headi a um novo nó terminal.

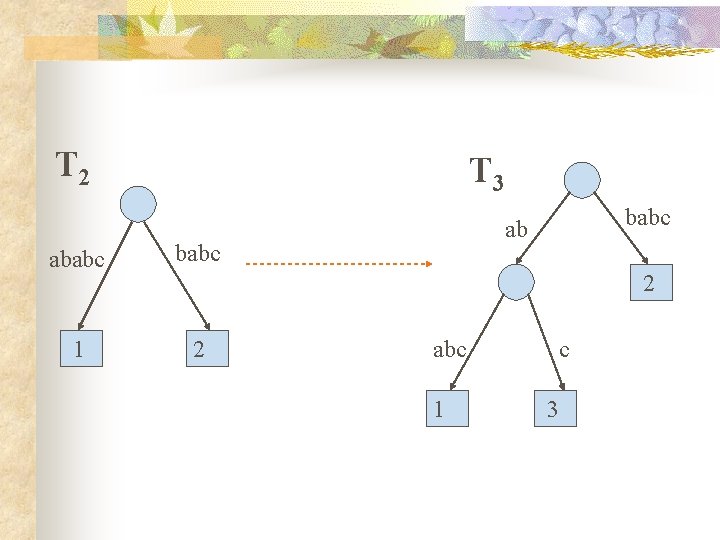
T 2 T 3 ababc 1 2 babc ab 2 abc 1 c 3

n Busca pelo locus estendido de headi n n Se headi-1 pode ser escrito como a , então é prefixo de headi. Suffix link: liga o locus de x ao locus de . gtagcagtcggacgagca sufi-1 sufi sufj-1 sufj

b abab. . . b 2 b ab b 3 b ababb. . . b 4 b babab. . . bbaa. . . ababb. . . S = b 5 abab 3 a 2 b 5 c

function fastfind (v: node; p: string): no; { p está contido em algum caminho iniciado em v } begin A partir de v, siga o caminho rotulado por p ; compare apenas o primeiro símbolo de cada aresta. Seja (w, ) o último nó implícito; se = então return w; senão return break(w, ); end

function slowfind (v: node; p: string): no; begin A partir de v, siga o caminho rotulado pelo maior prefixo de p, letra por letra. Seja (w, ) o último nó implícito; se = então return w; senão return break(w, ); end

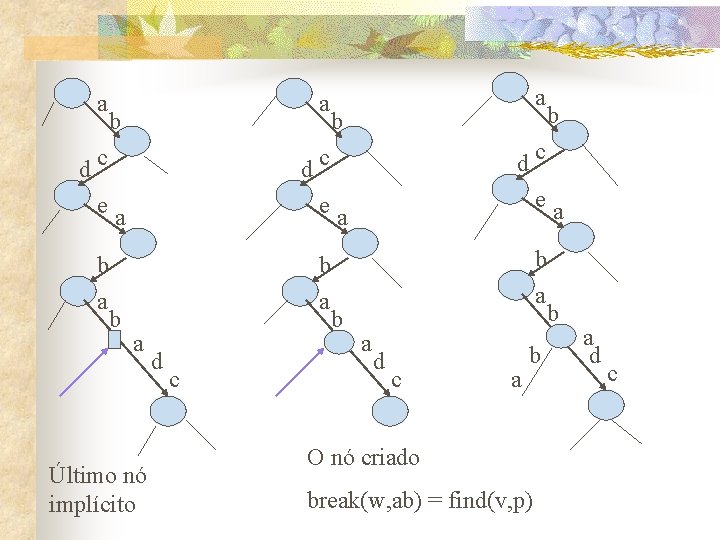
a a b dc ea dc dc e a ea b b a a Último nó implícito d c b b a d c a b O nó criado break(w, ab) = find(v, p) a d c

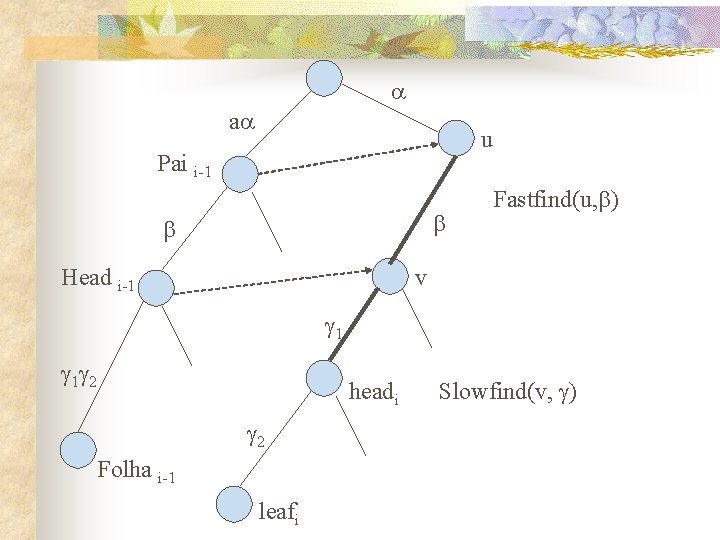
Algoritmo Mc. Creight; begin T : = árvore com dois nós e uma aresta rotulada p 1 for i: =2 to n do begin /* insere o proximo sufixo pi*/ rótulo da aresta (pai[headi-1], headi-1) rótulo da aresta (headi-1, leafi-1) u: = suf[pai[headi-1]]; v: = fastfind (u, );

Se v tem apenas 1 filho então {v é um nó recentemente inserido} headi : = v Senão headi : = slowfind(v, ); Suf[headi]: =v; Crie uma nova folha leafi; Faça leafi como filha de headi; Rotule a aresta (headi, leafi) de acordo; end.

a u Pai i-1 Head i-1 Fastfind(u, ) v 1 1 2 headi 2 Folha i-1 leafi Slowfind(v, )

Outros Algoritmos n Algoritmo de Weiner n n Incremental (como o de Mc. Creight) Processa o texto da direita para a esquerda Busca a partir do prefixo (+ complexo) Algoritmo de Ukkonen n n Construção da árvore on-line Tempo linear (alfabeto fixo)