rvores de Busca rvores de Busca Uma rvore

Árvores de Busca

Árvores de Busca Uma árvore que suporta eficientes operações de busca, inclusão e exclusão é chamada de árvore de busca. A árvore é usada para armazenar um conjunto finito de chaves obtidas de um conjunto totalmente ordenado de chaves K. Cada nó da árvore contém um ou mais chaves e todas as chaves na árvore são únicas, sem duplicação. A diferença entre uma árvore comum e uma árvore de busca é que, nesta última, as chaves não aparecem em nós arbitrários. Existe um critério de ordenação de dados que determina aonde cada chave pode figurar na árvore em relação às demais. Serão apresentadas as árvores de busca: n de M caminhos (M-Way) n binárias. 2

Binary Search Tree (BST) Definição (Árvore de busca M-way) Uma árvore de busca M-way T é um conjunto finito de chaves. Ou o conjunto é vazio, T = ; ou o conjunto é constituído de n sub árvores M-way T 1 , T 2 , . . . , Tn-1, e n-1 chaves, k 1 , k 2 , . . . , kn-1, T = {T 0, k 1, T 1, k 2, . . . , kn-1, Tn-1} aonde 2 n M, tal que as chaves e os nós satisfaçam às seguintes propriedades de ordenação de dados: n As chaves em cada nó são distintas e ordenadas, i. e. , k i<ki+1 para 1 i n-1 n Todas as chaves contidas na sub árvore T i-1 são menores do que ki. A árvore Ti-1 é chamada sub árvore da esquerda com respeito à chave ki. n Todas as chaves contidas na sub árvore T i são maiores do que ki. A árvore Ti+1 é chamada sub árvore da direita com respeito à chave ki. 3
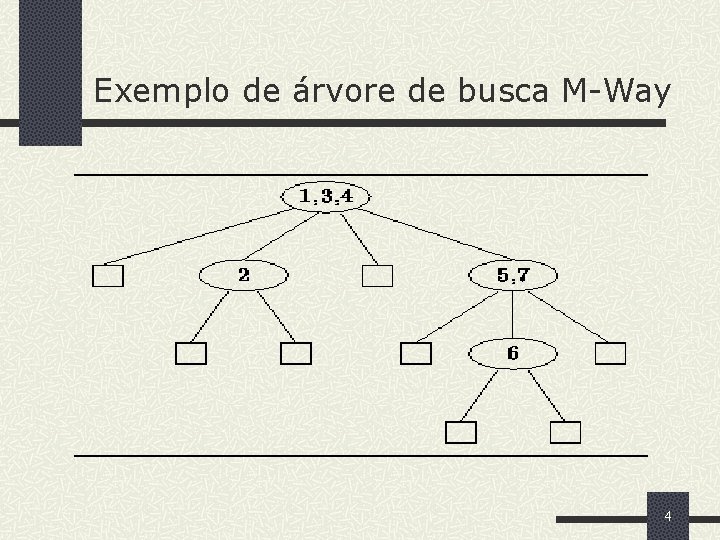
Exemplo de árvore de busca M-Way 4

Binary Search Tree (BST) Definição (Árvore Binária de Busca) A Árvore Binária de Busca T é um conjunto finito de chaves. Ou o conjunto é vazio, T = ; ou o conjunto consiste da raiz r e exatamente duas Árvores Binárias de Busca TL e TR , T={r, TL, TR}, tais que as seguintes propriedades sejam satisfeitas: 1. Todas as chaves contidas na sub árvore da esquerda, TL, são menores do que r. 2. Todas as chaves contidas na sub árvore da direita, TR , são maiores do que r. 5
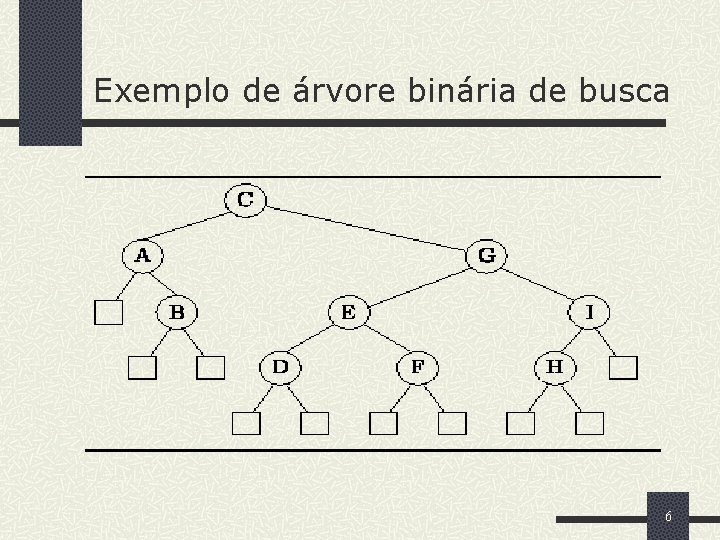
Exemplo de árvore binária de busca 6

Busca em Árvores de Busca M-Way Busca do objeto x inicia na raiz Se a raiz estiver vazia a busca falha As chaves contidas na raiz são examinadas para verificar se o objeto buscado está presente Se o objeto não estiver presente três casos podem ocorrer: n Objeto buscado é menor do que k 1 n a busca prossegue em T 0; n Objeto buscado é maior do que kn-1 n a busca prossegue em Tn-1; n Existe um i tal que ki < x < ki+1 n a busca prossegue em Ti 7

Busca em Árvores Binárias de Busca Semelhante à busca em árvores de busca M-Way Apenas cada nó só possui um objeto e duas sub árvores 8

Árvore Binária Perfeita Definição (Árvore Binária Perfeita) A Árvore Binária Perfeita de altura h 0 é um árvore binária T={r, TL, TR} com as propriedades: 1. Se h=0, então TL = e TR = . 2. Caso contrário, h>0, caso no qual ambos TL e TR são Árvores Binárias Perfeitas de altura h -1. 9

Implementação Java
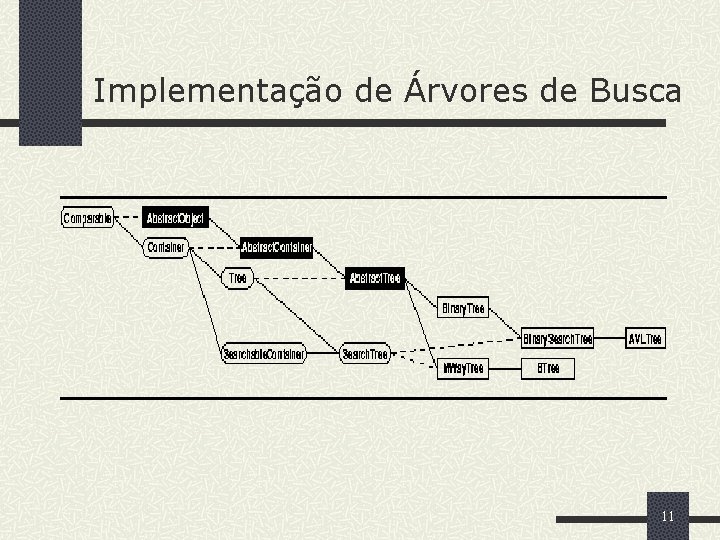
Implementação de Árvores de Busca 11

Interface Search. Tree // pgm 10_01. java public interface Search. Tree extends Tree, Searchable. Container { Comparable find. Min (); Comparable find. Max (); } 12

Classe Binary. Search. Tree // pgm 10_02. java public class Binary. Search. Tree extends Binary. Tree implements Search. Tree { //. . . } 13

Classe Association public class Association extends Abstract. Object { protected Comparable key; protected Object value; //. . . } // só aparece por causa de get. Key 14

Métodos da Classe Association public class Association extends Abstract. Object { protected Comparable key; protected Object value; public Association (Comparable key, Object value) { this. key = key; this. value = value; } public Association (Comparable key) { this (key, null); } public Comparable get. Key () { return key; } public Object get. Value () { return value; } //. . . } 15

Métodos da Classe Binary. Search. Tree get. Left. BST get. Right. BST find. Min insert attach. Key balance withdraw 16

Métodos get. Left. BST e get. Right. BST // pgm 10_03. java public class Binary. Search. Tree extends Binary. Tree implements Search. Tree { private Binary. Search. Tree get. Left. BST() { return (Binary. Search. Tree) get. Left(); } private Binary. Search. Tree get. Right. BST() { return (Binary. Search. Tree) get. Right(); } //. . . } 17

Método find // pgm 10_04. java public class Binary. Search. Tree extends Binary. Tree implements Search. Tree { public Comparable find (Comparable object) { if(is. Empty()) return null; int diff = object. compare((Comparable) get. Key()); if(diff == 0) return (Comparable) get. Key(); else if(diff < 0) return get. Left. BST(). find(object); else return get. Right. BST(). find(object); } 18 }

Método find. Min public Comparable find. Min () { if(is. Empty()) return null; else if(get. Left. BST(). is. Empty()) return (Comparable) get. Key(); else return get. Left. BST(). find. Min(); } //. . . 19

Inserção de itens em BST A inclusão de nós em árvores de busca deve ser precedida de uma operação de busca. Esta operação indica se o nó buscado já existe na árvore e, em caso de não existência, o local aonde deve ser feita a inclusão. Convém lembrar que uma busca sempre termina em folha e os nós a incluir serão incluídos como filhos da folha aonde se encerrou a busca. 20

Método insert (1) // pgm 10_05. java public class Binary. Search. Tree extends Binary. Tree implements Search. Tree { public void insert (Comparable object) { if(is. Empty()) attach. Key (object); 21

Método insert (2) else { int diff = object. compare((Comparable) get. Key()); if(diff == 0) throw new Illegal. Argument. Exception( “chave duplicada"); if(diff < 0) get. Left. BST(). insert(object); else get. Right. BST(). insert(object); } balance(); } } 22

Métodos attach. Key e balance public void attach. Key (Object object) { if(!is. Empty()) throw new Invalid. Operation. Exception(); key = object; left = new Binary. Search. Tree(); right = new Binary. Search. Tree(); } protected void balance() {} 23

Remoção de itens em BST A exclusão de nós em árvores de busca pode configurar um de 3 casos. n Se o nó não tiver filhos pode ser excluído sem exigir ajustamento da árvore. n Se o nó a excluir tiver apenas uma sub árvore, este nó pode ser excluído e deve ser substituído por seu filho único. n Se o nó a excluir tiver mais de um filho, para que ele possa ser excluído, deve ser substituído por seu antecessor ou seu sucessor em ordem infixa. O nó substituto deve ser excluído da sua posição gerando outro processo de exclusão. Considerando o caso do sucessor em ordem infixa, o nó a ser excluído deve ser substituído pelo nó obtido alcançando-se o nó mais à esquerda da sub árvore direita do nó a excluir. 24
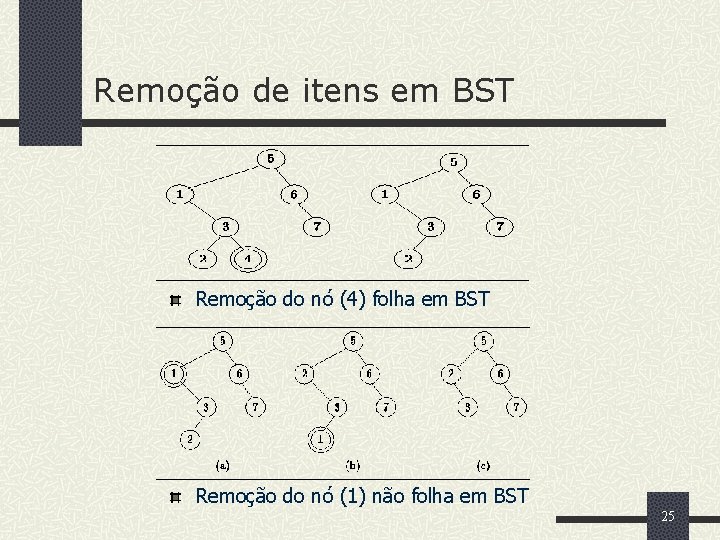
Remoção de itens em BST Remoção do nó (4) folha em BST Remoção do nó (1) não folha em BST 25

Método withdraw (1) // pgm 10_06. java public class Binary. Search. Tree extends Binary. Tree implements Search. Tree { public void withdraw (Comparable object) { if(is. Empty()) throw new Illegal. Argument. Exception( "objeto não encontrado") int diff = object. compare ((Comparable) get. Key()); if(diff == 0) { if(!get. Left. BST(). is. Empty()) { Comparable max = get. Left. BST(). find. Max(); key = max; get. Left. BST(). withdraw(max); } 26

Método withdraw (2) else if(!get. Right. BST(). is. Empty()) { Comparable min = get. Right. BST(). find. Min(); key = min; get. Right. BST(). withdraw(min); } else detach. Key(); } else if(diff < 0) get. Left. BST(). withdraw(object); else get. Right. BST(). withdraw(object); balance(); } //. . . } 27

Árvores de Busca AVL

Conceito de AVL Adelson-Velskii e Landis propuseram as condições de balanceamento para uma árvore binária que recebeu como sigla suas iniciais. Definição (Condição de equilíbrio AVL) Uma árvore binária vazia é AVL balanceada . Uma árvore binária não-vazia, T={r, TL, TR} , é AVL balanceada se tanto TL quanto TR forem AVL balanceadas e |h. Lh. R|<=1 aonde h. L é a altura of TL e h. R é a altura of TR. 29

Implementação de árvores AVL

Classe AVLTree // pgm 10_07. java public class AVLTree extends Binary. Search. Tree { protected int Height; //. . . } 31

Construtor // pgm 10_08. java public class AVLTree extends Binary. Search. Tree { protected int Height; public AVLTree() { Height = -1; } //. . . } 32

Métodos get. Height, adjust. Height e get. Balance. Factor public int get. Height () { return Height; } protected void adjust. Height() { if(is. Empty()) Height = -1; else Height = 1 + Math. max(left. get. Height(), right. get. Height()); } protected int get. Balance. Factor() { if(is. Empty()) return 0; else return left. get. Height() - right. get. Height(); } 33

Inserção de itens em Árvores AVL 1 o. Passo – Inserir o item 2 o. Passo – Balancear a árvore 34

Balanceamento de Árvores AVL O balanceamento de árvores AVL é feito por operações chamadas de rotações, que podem ser: n Rotações simples (LL e RR) n Rotações duplas (LR e RL) 35

Rotações simples A rotação LL ocorre quando um nó (B) tem a sub árvore da esquerda maior do que a da direita e seu filho da esquerda (A) tem sub árvore da esquerda maior do que a da direita A rotação RR ocorre quando um nó (B) tem a sub árvore da direita maior do que a da esquerda e seu filho da direita (A) tem sub árvore da direita maior do que a da esquerda 36

Rotações duplas A rotação LR ocorre quando um nó (C) tem a sub árvore da esquerda maior do que a da direita e seu filho da esquerda (A) tem sub árvore da direita maior do que a da esquerda. Aplica-se uma rotação RR a A seguida de uma rotação LL aplicada a C. A rotação RL ocorre quando um nó (C) tem a sub árvore da direita maior do que a da esquerda e seu filho da direita (A) tem sub árvore da esquerda maior do que a da direita. Aplica-se uma rotação LL a A seguida de uma rotação RR aplicada a C. 37
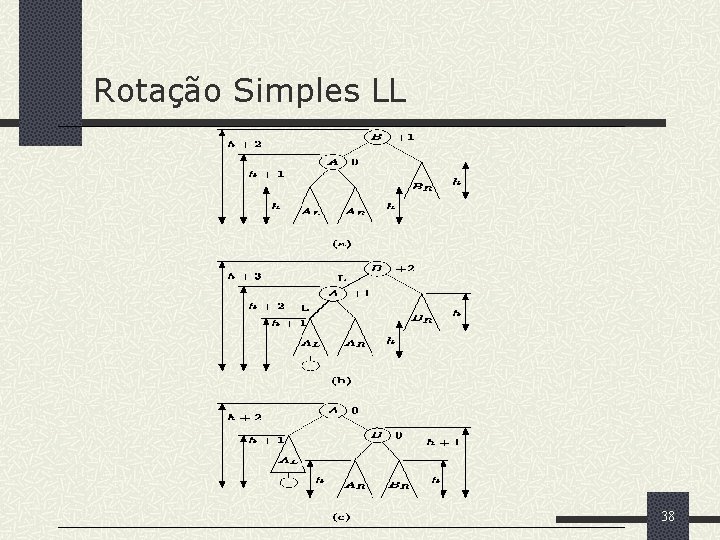
Rotação Simples LL 38

Propriedades das rotações simples Existem três propriedades importantes da rotação LL: 1. A rotação não destrói a propriedade de ordenação de dados e, portanto, o resultado ainda é uma árvore de busca. A sub árvore AL permanece entre os nós A e B, e a sub árvore BR fica à direita do nó B. 2. Após a rotação tanto A quanto B são AVL balanceadas. Os nós A e B ficam com fator de balanceamento igual a zero. 3. Após a rotação a árvore permanece com a altura original. A inclusão do item não aumenta a altura da árvore. 39
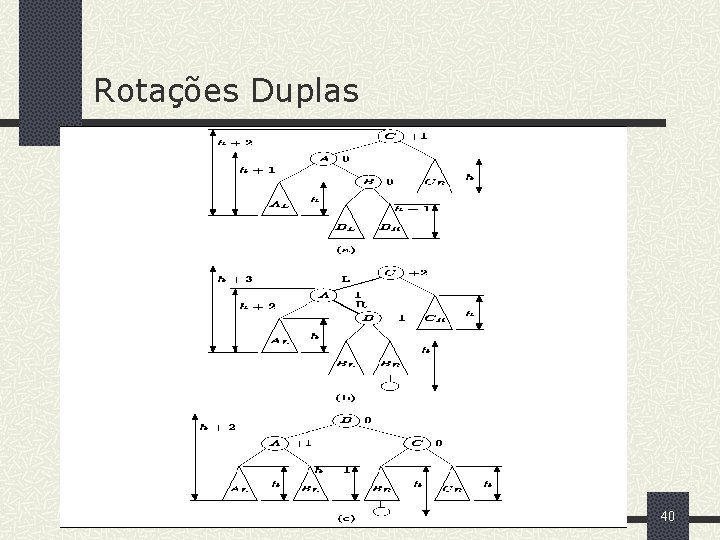
Rotações Duplas 40

Balanceamento de árvores AVL Os desbalanceamentos e as rotações de equilíbrio correspondentes podem ser enquadrados em seis categorias, ou casos, adiante descritos. O ancestral mais novo, desbalanceado, do novo nó inserido é ya. Seu filho na direção do desbalanceamento é s. Os sufixos l e r representam filho mais velho e filho mais novo, respectivamente: 41

Categorias de rotações 1 o caso: O novo nó é incluído na sub árvore esquerda do nó ya. Este caso tem solução chamada de rightrotation ou rotação LL 2 o caso: O novo nó é incluído na sub árvore direita do nó ya. Este caso tem solução chamada de leftrotation ou rotação RR 3 o caso: O novo é incluído na sub árvore esquerda da sub árvore direita do filho mais velho de ya (rotação LR) 4 o caso: O novo nó é incluído na sub árvore direita do filho mais velho de ya (LR) 5 o caso: O novo nó é incluído na sub árvore direita da sub árvore esquerda do filho mais novo de ya (RL) 6 o caso: O novo nó incluído na sub árvore esquerda do filho mais novo de ya (RL) 42

Rotação LL 43
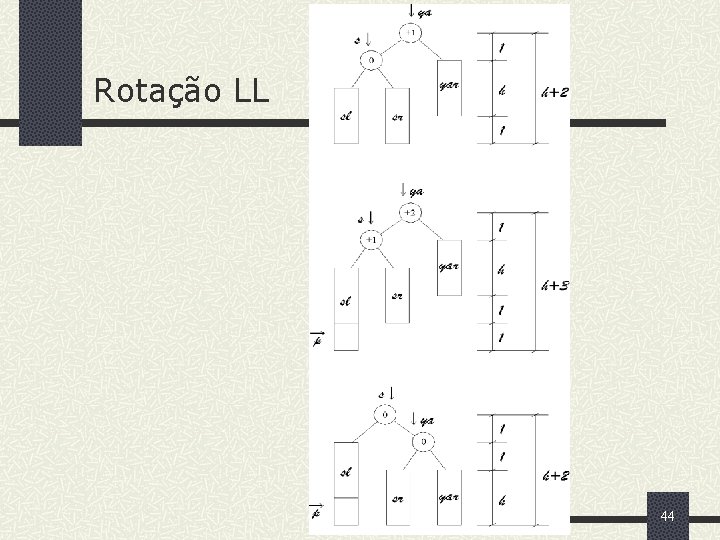
Rotação LL 44

Rotação RR 45
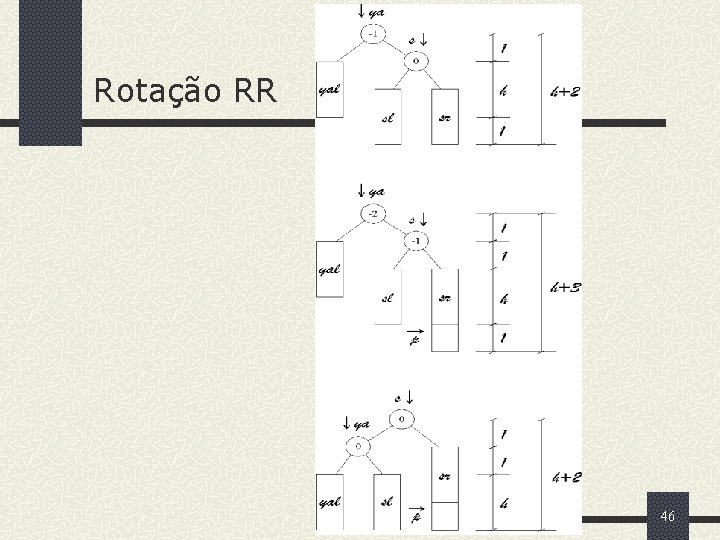
Rotação RR 46

Rotação LR 47
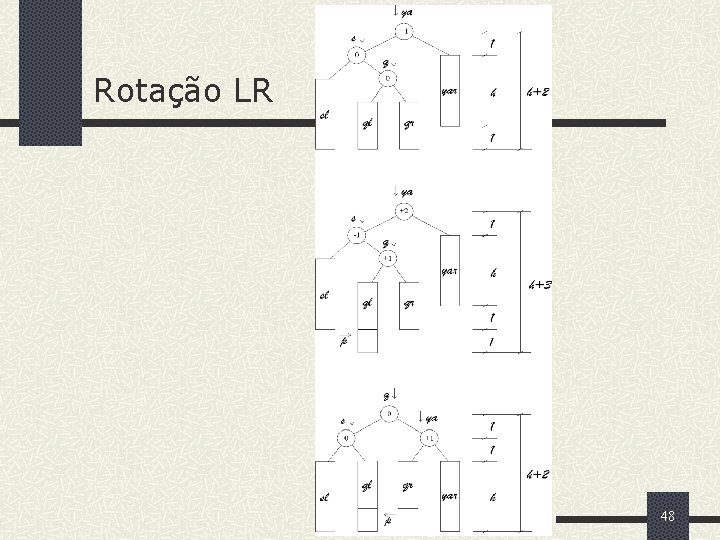
Rotação LR 48

Rotações LR e RL 49
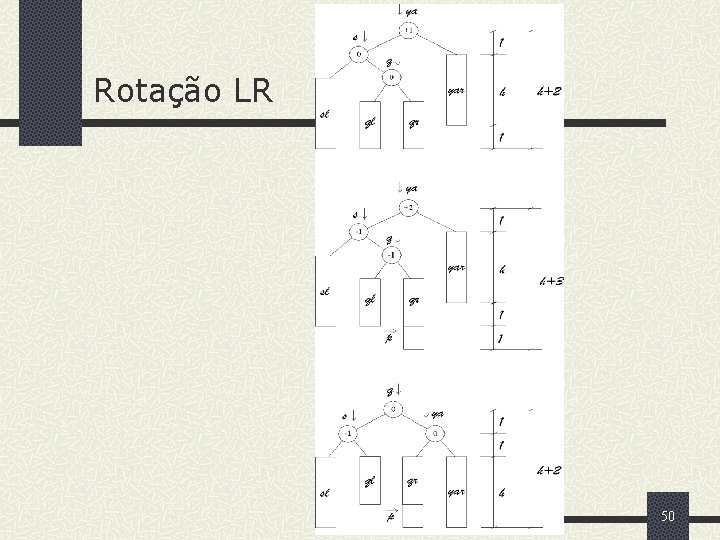
Rotação LR 50

Rotação RL 51

Classe AVLTree public class AVLTree extends Binary. Search. Tree { protected int Height; //. . . } 52

Métodos height, get. Height e get. Balance. Factor (1) public class AVLTree extends Binary. Search. Tree { protected int height; public AVLTree() { height = -1; } public int get. Height() { return height; } protected void adjust. Height() { if(is. Empty()) height = -1; else height = 1 + Math. max (left. get. Height(), right. get. Height()); } 53

Métodos height, get. Height e get. Balance. Factor (2) protected int get. Balance. Factor() { if(is. Empty()) return 0; else return left. get. Height() - right. get. Height(); } //. . . } 54

Método do. LLRotation (1) // pgm 10_09. java public class AVLTree extends Binary. Search. Tree { protected int Height; protected void do. LLRotation() { if(is. Empty()) throw new Invalid. Operation. Exception(); Binary. Tree tmp = right; right = left; left = right. left; right. left = right; right = tmp; 55

Método do. LLRotation (2) Object tmp. Obj = key; key = right. key; right. key = tmp. Obj; get. Right. AVL(). adjust. Height(); } //. . . } 56

Método do. RRRotation (1) public class AVLTree extends Binary. Search. Tree { protected int Height; protected void do. RRRotation() { if(is. Empty()) throw new Invalid. Operation. Exception(); Binary. Tree tmp = left; left = right; right = left. right; left. right = left; left = tmp; 57

Método do. RRRotation (2) Object tmp. Obj = key; key = left. key; left. key = tmp. Obj; get. Left. AVL(). adjust. Height(); } //. . . } 58

Método do. LRRotation // pgm 10_10. java public class AVLTree extends Binary. Search. Tree { protected int Height; protected void do. LRRotation() { if(is. Empty()) throw new Invalid. Operation. Exception(); get. Left. AVL(). do. RRRotation(); do. LLRotation(); } //. . . } 59

Método do. RLRotation public class AVLTree extends Binary. Search. Tree { protected int Height; protected void do. RLRotation() { if(is. Empty()) throw new Invalid. Operation. Exception(); get. Right. AVL(). do. LLRotation(); do. RRRotation(); } //. . . } 60

Método balance (1) // pgm 10_11. java public class AVLTree extends Binary. Search. Tree { protected int Height; protected void balance() { adjust. Height(); if(get. Balance. Factor() > 1) { if(get. Left. AVL(). get. Balance. Factor() > 0) do. LLRotation(); else do. LRRotation(); } 61

Método balance (2) else if(get. Balance. Factor() < -1) { if(get. Right. AVL(). get. Balance. Factor() < 0) do. RRRotation(); else do. RLRotation(); } } //. . . } 62

Método attach. Key // pgm 10_12. java public class AVLTree extends Binary. Search. Tree { protected int Height; public void attach. Key(Object object) { if(!is. Empty()) throw new Invalid. Operation. Exception(); key = object; left = new AVLTree(); right = new AVLTree(); Height = 0; } //. . . } 63

Remoção de itens de Árvores AVL

Método detach. Key // pgm 10_13. java public class AVLTree extends Binary. Search. Tree { protected int Height; public Object detach. Key() { Height = -1; return super. detach. Key(); } //. . . } 65

Árvores de Busca de Múltiplos caminhos
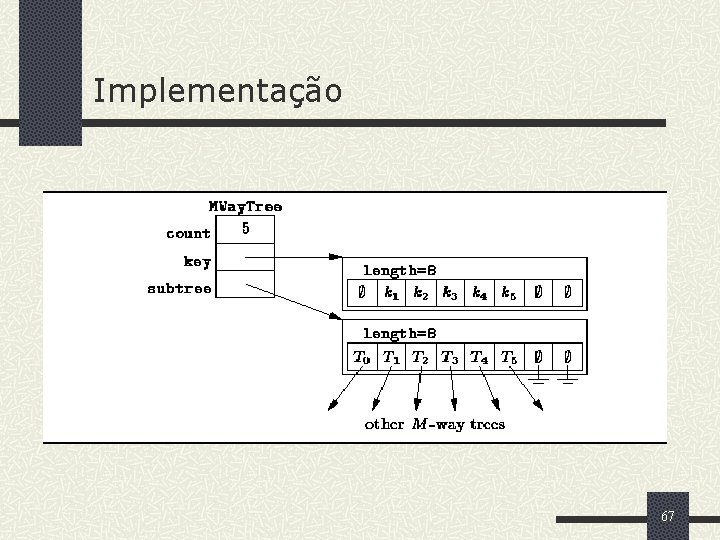
Implementação 67

Classe Mway. Tree: Métodos construtor e get. M // pgm 10_14. java public class MWay. Tree extends Abstract. Tree implements Search. Tree { protected Comparable key[]; protected MWay. Tree subtree[]; public MWay. Tree(int m) { if(m < 2) throw new Illegal. Argument. Exception(“grau inválido"); key = new Comparable[m]; subtree = new MWay. Tree[m]; } int get. M() { return subtree. length; } //. . . 68 }

Travessia em ordem infixa de árvores binárias de busca Travessias infixas de árvores binárias são da forma: n Percorrer a sub árvore da esquerda n Visitar a raiz n Percorre a sub árvore da direita Isto corresponde a, em uma travessia infixa de uma árvore binária de busca, visitar a todos os registros armazenados na árvore em ordem 69

Travessia em ordem infixa Travessias infixas não são definidas para árvores N-arias Em árvores de busca M-Way a travessia infixa é definida como a visita a todos os registros armazenados na árvore em ordem 70

Travessia de um nó de uma árvore de busca M-Way . . . Percorrer a sub árvore T 0 Visitar o objeto k 1 Percorrer a sub árvore T 1 Visitar o objeto k 2 Percorrer a sub árvore T 2 Visitar o objeto kn-1 Percorrer a sub árvore Tn-1 71

Método depth. First. Traversal (1) // pgm 10_15. java public class MWay. Tree extends Abstract. Tree implements Search. Tree { protected Comparable key[]; protected MWay. Tree subtree[]; public void depth. First. Traversal (Pre. Post. Visitor visitor) { if(!is. Empty()) { for(int i = 0; i <= count + 1; ++i) { 72
![Método depth. First. Traversal (2) if(i >= 2) visitor. post. Visit(key[i - 1]); if(i Método depth. First. Traversal (2) if(i >= 2) visitor. post. Visit(key[i - 1]); if(i](http://slidetodoc.com/presentation_image_h/a6897d7ae09a3d09059916121886a0be/image-73.jpg)
Método depth. First. Traversal (2) if(i >= 2) visitor. post. Visit(key[i - 1]); if(i >= 1 && i <= count) visitor. in. Visit(key[i]); if(i <= count - 1) visitor. pre. Visit(key[i + 1]); if(i <= count) subtree[i]. depth. First. Traversal(visitor); } } 73

Busca linear de itens em Árvores M-Way

Método find (1) // pgm 10_16. java public class MWay. Tree extends Abstract. Tree implements Search. Tree { protected Comparable key[]; protected MWay. Tree subtree[]; public Comparable find(Comparable object) { if(is. Empty()) return null; int i; 75

Método find (2) for(i = count; i > 0; --i) { int diff = object. compare(key[i]); if(diff == 0) return key[i]; if(diff > 0) break; } return subtree[i]. find(object); } //. . . } 76

Inclusão de itens

Método insert (1) // pgm 10_18. java public void insert (Comparable object) { if(is. Empty()) { subtree[0] = new MWay. Tree(get. M()); key[1] = object; subtree[1] = new MWay. Tree(get. M()); count = 1; } else { int index = find. Index(object); if(index != 0 && object. is. EQ(key[index])) throw new Illegal. Argument. Exception (“chave duplicada"); 78

Método insert (2) if(!is. Full()) { for(int i = count; i > index; --i) { key[i + 1] = key[i]; subtree[i + 1] = subtree[i]; } key[index + 1] = object; subtree[index + 1] = new MWay. Tree(get. M()); ++count; } else subtree[index]. insert(object); } } 79

Remoção de itens

Método withdraw (1) public void withdraw (Comparable object) { if(is. Empty()) throw new Illegal. Argument. Exception ("objeto não encontrado"); int index = find. Index(object); if(index != 0 && object. is. EQ(key[index])) { if(!subtree[index - 1]. is. Empty()) { Comparable max = subtree[index 1]. find. Max(); key[index] = max; subtree[index - 1]. withdraw(max); } else 81
![Método withdraw (2) if(!subtree[index]. is. Empty()) { Comparable min = subtree[index]. find. Min(); key[index] Método withdraw (2) if(!subtree[index]. is. Empty()) { Comparable min = subtree[index]. find. Min(); key[index]](http://slidetodoc.com/presentation_image_h/a6897d7ae09a3d09059916121886a0be/image-82.jpg)
Método withdraw (2) if(!subtree[index]. is. Empty()) { Comparable min = subtree[index]. find. Min(); key[index] = min; subtree[index]. withdraw(min); } else { --count; int i; for(i = index; i <= count; ++i) { key[i] = key[i + 1]; subtree[i] = subtree[i + 1]; } 82
![Método withdraw (3) key[i] = null; subtree[i] = null; if(count == 0) subtree[0] = Método withdraw (3) key[i] = null; subtree[i] = null; if(count == 0) subtree[0] =](http://slidetodoc.com/presentation_image_h/a6897d7ae09a3d09059916121886a0be/image-83.jpg)
Método withdraw (3) key[i] = null; subtree[i] = null; if(count == 0) subtree[0] = null; } } else subtree[index]. withdraw(object); } 83

Implementação C++
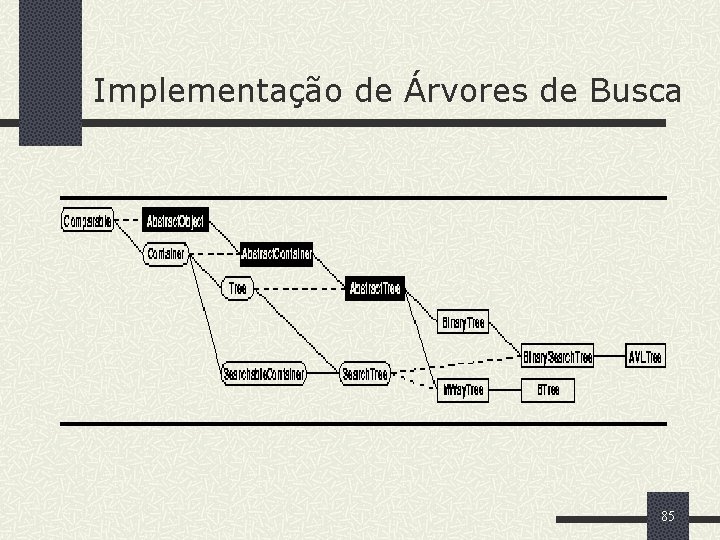
Implementação de Árvores de Busca 85

Definição da Classe Search. Tree // pgm 10_01. cpp class Search. Tree : public virtual Tree, public virtual Searchable. Container { public: virtual Object& Find. Min() const = 0; virtual Object& Find. Max() const = 0; }; 86

Definição da Classe BST // pgm 10_02. cpp class BST : public Binary. Tree, public Search. Tree { protected: virtual void Attach. Key(Object&); virtual Object& Detach. Key(); virtual void Balance(); public: BST& Left() const; BST& Right() const; //. . . }; 87

Funções da Classe Binary. Search. Tree left right find. Min insert attach. Key withdraw detach. Key 88

Definições da Função Membro Left e Rigth da Classe BST // pgm 10_03. cpp BST& BST: : Left() const { return dynamic_cast<BST&>(Binary. Tree: : Left ()); } BST& BST: : Right() const { return dynamic_cast<BST&>(Binary. Tree: : Right ()); } 89

Definições da Função Membro Find e Find. Min da Classe BST (1) // pgm 10_04. cpp Object& BST: : Find(Object const& object) const { if(Is. Empty ()) return Null. Object: : Instance(); int const diff = object. Compare(*key); if(diff == 0) return *key; else if(diff < 0) return Left(). Find(object); else return Right(). Find(object); } 90

Definições da Função Membro Find e Find. Min da Classe BST (2) Object& BST: : Find. Min() const { if(Is. Empty ()) return Null. Object: : Instance(); else if(Left(). Is. Empty()) return *key; else return Left(). Find. Min(); } 91

Inserção de itens em BST A inclusão de nós em árvores de busca deve ser precedida de uma operação de busca. Esta operação indica se o nó buscado já existe na árvore e, em caso de não existência, o local aonde deve ser feita a inclusão. Convém lembrar que uma busca sempre termina em folha e os nós a incluir serão incluídos como filhos da folha aonde se encerrou a busca. 92

Definições da Função Membro Insert, Attach. Key e Balance da Classe BST (1) // pgm 10 { _05. cpp void BST: : Insert(Object& object) { if(Is. Empty ()) Attach. Key(object); else int const diff = object. Compare(*key); if(diff == 0) throw invalid_argument(“chave duplicada"); if(diff < 0) Left(). Insert(object); else Right(). Insert(object); } Balance(); } 93

Definições da Função Membro Insert, Attach. Key e Balance da Classe BST (2) void BST: : Attach. Key(Object& object) { if(!Is. Empty ()) throw domain_error("operação inválida"); key = &object; left = new BST(); right = new BST(); } void BST: : Balance() {} 94

Remoção de itens em BST A exclusão de nós em árvores de busca pode configurar um de 3 casos. n Se o nó não tiver filhos pode ser excluído sem exigir ajustamento da árvore. n Se o nó a excluir tiver apenas uma sub árvore, este nó pode ser excluído e deve ser substituído por seu filho único. n Se o nó a excluir tiver mais de um filho, para que ele possa ser excluído, deve ser substituído por seu antecessor ou seu sucessor em ordem infixa. O nó substituto deve ser excluído da sua posição gerando outro processo de exclusão. Considerando o caso do sucessor em ordem infixa, o nó a ser excluído deve ser substituído pelo nó obtido alcançando-se o nó mais à esquerda da sub árvore direita do nó a excluir. 95
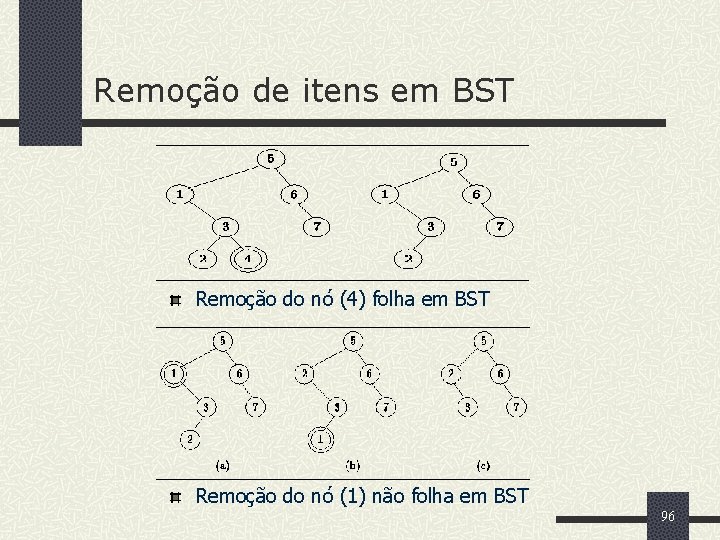
Remoção de itens em BST Remoção do nó (4) folha em BST Remoção do nó (1) não folha em BST 96

Definições da Função Membro Withdraw e Detach. Key da Classe BST (1) // pgm 10_06. cpp void BST: : Withdraw(Object& object) { if(Is. Empty ()) throw invalid_argument("objeto não encontrado"); int const diff = object. Compare(*key); if(diff == 0) { if(!Left(). Is. Empty()) { Object& max = Left(). Find. Max(); key = &max; Left(). Withdraw(max); } 97

Definições da Função Membro Withdraw e Detach. Key da Classe BST (2) else if(!Right(). Is. Empty()) { Object& min = Right(). Find. Min(); key = &min; Right(). Withdraw(min); } else Detach. Key(); } else if(diff < 0) Left(). Withdraw(object); else Right(). Withdraw(object); Balance(); } 98

Definições da Função Membro Withdraw e Detach. Key da Classe BST (3) Object& BST: : Detach. Key() { if(!Is. Leaf ()) throw domain_error("operação inválida"); Object& result = *key; delete left; delete right; key = 0; left = 0; right = 0; return result; } 99

Implementação de árvores AVL

Conceito de AVL Adelson-Velskii e Landis propuseram as condições de balanceamento para uma árvore binária que recebeu como sigla suas iniciais. Definição (Condição de equilíbrio AVL) Uma árvore binária vazia é AVL balanceada . Uma árvore binária não-vazia, T={r, TL, TR} , é AVL balanceada se tanto TL quanto TR forem AVL balanceadas e |h. Lh. R|<=1 aonde h. L é a altura of TL e h. R é a altura of TR. 101

Implementação de árvores AVL

Definição da Classe AVLTree (1) // pgm 10_07. cpp class AVLTree : public BST { protected: int height; int Balance. Factor() const; void Adjust. Height(); void LLRotation(); void LRRotation(); void RLRotation(); void Attach. Key(Object&); Object& Detach. Key(); void Balance(); 103

Definição da Classe AVLTree (2) public: AVLTree(); int Height() const; AVLTree& Left() const; AVLTree& Right() const; }; 104

Definições da Função Membro Height, Adjust. Height e Balance. Factor e do Construtor da Classe AVLTree (1) // pgm 10_08. cpp AVLTree: : AVLTree() : BST(), height(-1) {} int AVLTree: : Height() const { return height; } void AVLTree: : Adjust. Height() { if(Is. Empty ()) height = -1; else height = Max(left->Height(), right->Height()) + 1; } 105

Definições da Função Membro Height, Adjust. Height e Balance. Factor e do Construtor da Classe AVLTree (2) int AVLTree: : Balance. Factor() const { if(Is. Empty ()) return 0; else return left->Height() - right->Height(); } 106

Definição da Função Membro LLRotation da Classe AVLTree // pgm 10_09. cpp void AVLTree: : LLRotation() { if(Is. Empty ()) throw domain_error(“rotação inválida"); Binary. Tree* const tmp = right; right = left; left = Right(). left; Right(). left = Right(). right; Right(). right = tmp; Object* const tmp. Obj = key; key = Right(). key; Right(). key = tmp. Obj; Right(). Adjust. Height(); } 107

Definição da Função Membro LRRotation da Classe AVLTree // pgm 10_10. cpp void AVLTree: : LRRotation() { if(Is. Empty ()) throw domain_error("rotação inválida"); Left(). RRRotation(); LLRotation(); } 108

Definição da Função Membro Balance da Classe AVLTree // pgm 10_11. cpp void AVLTree: : Balance() { Adjust. Height(); if(abs(Balance. Factor ()) > 1) { if(Balance. Factor() > 0) { if(Left(). Balance. Factor() > 0) LLRotation(); else LRRotation(); } else { if(Right(). Balance. Factor() < 0) RRRotation(); else RLRotation(); } } } 109

Definições das Função Membro Attach. Key e Detach. Key da Classe AVLTree // pgm 10_12. cpp void AVLTree: : Attach. Key(Object& object) { if(!Is. Empty ()) throw domain_error("operação inválida"); key = &object; left = new AVLTree(); right = new AVLTree(); height = 0; } Object& AVLTree: : Detach. Key() { height = -1; return BST: : Detach. Key (); } 110

Definição da Classe MWay. Tree // pgm 10_13. cpp class MWay. Tree : public Search. Tree { protected: unsigned int const m; unsigned int number. Of. Keys; Array<Object*> key; Array<MWay. Tree*> subtree; unsigned int Find. Index(Object const&) const; public: MWay. Tree(unsigned int); ~MWay. Tree(); Object& Key(unsigned int) const; MWay. Tree& Subtree(unsigned int) const; //. . . }; 111

Definição da Função Membro Depth. First. Traversal da Classe MWay. Tree // pgm 10_14. cpp void MWay. Tree: : Depth. First. Traversal( Pre. Post. Visitor& visitor) const { if(!Is. Empty ()) { for(int i = 0; i <= number. Of. Keys + 1; ++i) { if(i >= 2) visitor. Post. Visit(*key [i - 1]); if(i >= 1 && i <= number. Of. Keys) visitor. Visit(*key [i]); if(i <= number. Of. Keys - 1) visitor. Pre. Visit(*key [i + 1]); if(i <= count) subtree[i]->Depth. First. Traversal (visitor); } } 112 }

Definição (Linear Search) da Função Membro Find da Classe MWay. Tree // pgm 10_15. cpp Object& MWay. Tree: : Find(Object const& object) const { if(Is. Empty ()) return Null. Object: : Instance(); unsigned int i = number. Of. Keys; while(i > 0) { int const diff = object. Compare(*key[i]); if(diff == 0) return *key[i]; if(diff > 0) break; --i; } return subtree[i]->Find(object); } 113

Definições (Binary Search) da Função Find. Index e Find da Classe MWay. Tree (1) // pgm 10_16. cpp unsigned int MWay. Tree: : Find. Index(Object const& object) const { if(Is. Empty ()) throw domain_error("operação inválida"); if(object < *key[1]) return 0; unsigned int left = 1; unsigned int right = number. Of. Keys; while(left < right) { int const middle = (left + right + 1) / 2; if(object >= *key[middle]) left = middle; else right = middle - 1 U; } return left; 114 }

Definições (Binary Search) da Função Find. Index e Find da Classe MWay. Tree (2) Object& MWay. Tree: : Find(Object const& object) const { if(Is. Empty ()) return Null. Object: : Instance(); unsigned int const index = Find. Index(object); if(index != 0 && object == *key[index]) return *key[index]; else return subtree[index]->Find(object); } 115

Definição da Função Membro Insert da Classe MWay. Tree (1) // pgm 10_17. cpp void MWay. Tree: : Insert(Object& object) { if(Is. Empty ()) { subtree[0] = new MWay. Tree(m); key[1] = &object; subtree[1] = new MWay. Tree(m); number. Of. Keys = 1; } else { unsigned int const index = Find. Index(object); if(index != 0 && object == *key[index]) throw invalid_argument(“chave duplicada"); if(number. Of. Keys < m - 1 U) { 116

Definição da Função Membro Insert da Classe MWay. Tree (2) for(unsigned int i = number. Of. Keys; i > index; --i) { key[i + 1] = key[i]; subtree[i + 1] = subtree[i]; } key[index + 1] = &object; subtree[index + 1] = new MWay. Tree(m); ++number. Of. Keys; } else subtree[index]->Insert(object); } } 117

Definição da Função Membro Withdraw da Classe MWay. Tree (1) // pgm 10_18. cpp void MWay. Tree: : Withdraw(Object& object) { if(Is. Empty ()) throw invalid_argument("objeto não encontrado"); unsigned int const index = Find. Index(object); if(index != 0 && object == *key[index]) { if(!subtree[index - 1 U]->Is. Empty()) { Object& max = subtree[index - 1 U]->Find. Max(); key[index] = &max; subtree[index - 1 U]->Withdraw(max); } 118
![Definição da Função Membro Withdraw da Classe MWay. Tree (2) else if(!subtree[index]->Is. Empty()) { Definição da Função Membro Withdraw da Classe MWay. Tree (2) else if(!subtree[index]->Is. Empty()) {](http://slidetodoc.com/presentation_image_h/a6897d7ae09a3d09059916121886a0be/image-119.jpg)
Definição da Função Membro Withdraw da Classe MWay. Tree (2) else if(!subtree[index]->Is. Empty()) { Object& min = subtree[index]->Find. Min(); key[index] = &min; subtree[index]->Withdraw(min); } else { --number. Of. Keys; delete subtree[index]; for(unsigned int i = index; i <= number. Of. Keys; ++i) { key[i] = key[i + 1]; subtree[i] = subtree[i + 1]; } 119

Definição da Função Membro Withdraw da Classe MWay. Tree (3) if(number. Of. Keys == 0) delete subtree[0]; } } else subtree[index]->Withdraw(object); } 120

Definição da Classe BTree // pgm 10_19. cpp class BTree : public MWay. Tree { BTree* parent; void Insert. Pair(Object&, BTree&); void Attach. Key(unsigned int, Object&); void Attach. Subtree(unsigned int, MWay. Tree&); Object& Insert. Key(unsigned int, Object&); BTree& Insert. Subtree(unsigned int, BTree&); void Attach. Left. Half. Of(BTree const&); void Attach. Right. Half. Of(BTree const&, Object&, BTree&); public: BTree(unsigned int); BTree(unsigned int, BTree&); void Insert(Object&); void Withdraw(Object&); }; 121

Definição da Função Membro Insert da Classe BTree (1) // pgm 10_20. cpp void BTree: : Insert(Object& object) { if(Is. Empty ()) { if(parent == 0) { Attach. Subtree(0, *new BTree(m, *this)); Attach. Key(1, object); Attach. Subtree(1, *new BTree(m, *this)); number. Of. Keys = 1; } else parent->Insert. Pair(object, *new BTree(m, *parent)); } 122

Definição da Função Membro Insert da Classe BTree (2) else { unsigned int const index = Find. Index(object); if(index != 0 && object == *key[index]) throw invalid_argument(“chave duplicada"); subtree[index]->Insert(object); } } 123

Definição da Função Membro Insert. Pair da Classe BTree (1) // pgm 10_21. cpp void BTree: : Insert. Pair(Object& object, BTree& child) { unsigned int const index = Find. Index(object); BTree& extra. Tree = Insert. Subtree(index + 1, child); Object& extra. Key = Insert. Key(index + 1, object); if(++number. Of. Keys == m) { if(parent == 0) { BTree& left = *new BTree(m, *this); BTree& right = *new BTree(m, *this); left. Attach. Left. Half. Of(*this); 124

Definição da Função Membro Insert. Pair da Classe BTree (2) right. Attach. Right. Half. Of(*this, extra. Key, extra. Tree); Attach. Subtree(0, left); Attach. Key(1, *key[(m + 1)/2]); Attach. Subtree(1, right); number. Of. Keys = 1; } else { number. Of. Keys =(m + 1) / 2 - 1; BTree& right = *new BTree(m, *parent); right. Attach. Right. Half. Of(*this, extra. Key, extra. Tree); parent->Insert. Pair(*key[(m + 1)/2], right); } } } 125
- Slides: 125