RUANG DIMENSI TIGA http furahasekai wordpress com MATERI

RUANG DIMENSI TIGA http: //furahasekai. wordpress. com

MATERI: TITIK, GARIS DAN BIDANG LUAS PERMUKAAN DAN VOLUME BANGUN RUANG http: //furahasekai. wordpress. com PROYEKSI MENGGAMBAR BANGUN RUANG MENENTUKAN JARAK PADA BANGUN RUANG SUDUT-SUDUT DALAM RUANG MENGGAMBAR IRISAN BANGUN RUANG

TITIK, GARIS, DAN BIDANG http: //furahasekai. wordpress. com

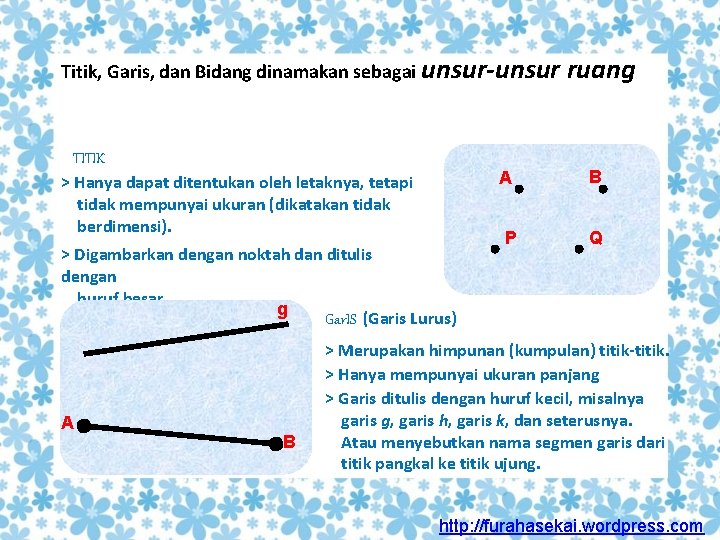
Titik, Garis, dan Bidang dinamakan sebagai unsur-unsur TITIK > Hanya dapat ditentukan oleh letaknya, tetapi tidak mempunyai ukuran (dikatakan tidak berdimensi). > Digambarkan dengan noktah dan ditulis dengan huruf besar. g Gar. IS (Garis Lurus) A B ruang A B P Q > Merupakan himpunan (kumpulan) titik-titik. > Hanya mempunyai ukuran panjang > Garis ditulis dengan huruf kecil, misalnya garis g, garis h, garis k, dan seterusnya. Atau menyebutkan nama segmen garis dari titik pangkal ke titik ujung. http: //furahasekai. wordpress. com

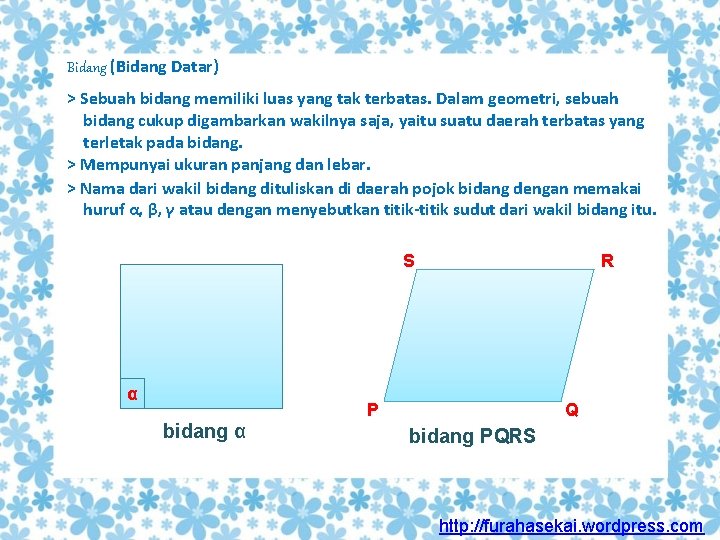
Bidang (Bidang Datar) > Sebuah bidang memiliki luas yang tak terbatas. Dalam geometri, sebuah bidang cukup digambarkan wakilnya saja, yaitu suatu daerah terbatas yang terletak pada bidang. > Mempunyai ukuran panjang dan lebar. > Nama dari wakil bidang dituliskan di daerah pojok bidang dengan memakai huruf α, β, γ atau dengan menyebutkan titik-titik sudut dari wakil bidang itu. S α bidang α R P Q bidang PQRS http: //furahasekai. wordpress. com

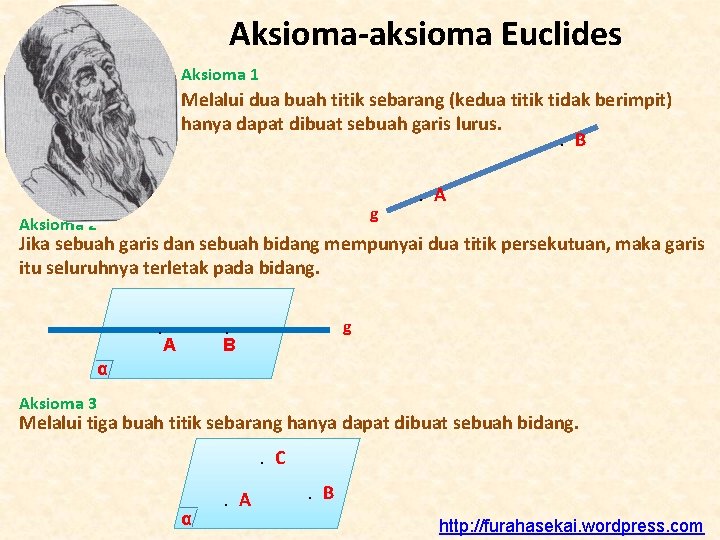
Aksioma Garis dan Bidang Aksioma atau postulat adalah pernyataan yang diandaikan benar dalam sebuah sistem dan kebenaran itu diterima tanpa pembuktian. Dalam geometri ruang ada tiga buah aksioma yang penting. Ketiga buah aksioma itu diperkenalkan oleh Euclides-(+ 300 SM), seorang ahli matematika dari Alexandria. http: //furahasekai. wordpress. com

Aksioma-aksioma Euclides Aksioma 1 Melalui dua buah titik sebarang (kedua titik tidak berimpit) hanya dapat dibuat sebuah garis lurus. . B g Aksioma 2 . A Jika sebuah garis dan sebuah bidang mempunyai dua titik persekutuan, maka garis itu seluruhnya terletak pada bidang. . . A g B α Aksioma 3 Melalui tiga buah titik sebarang hanya dapat dibuat sebuah bidang. . C α . A . B http: //furahasekai. wordpress. com

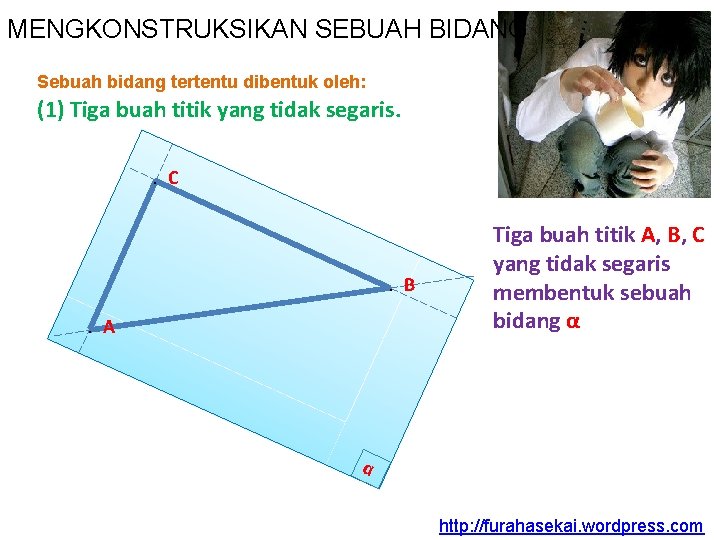
MENGKONSTRUKSIKAN SEBUAH BIDANG Sebuah bidang tertentu dibentuk oleh: (1) Tiga buah titik yang tidak segaris. . C . B. A Tiga buah titik A, B, C yang tidak segaris membentuk sebuah bidang α α http: //furahasekai. wordpress. com

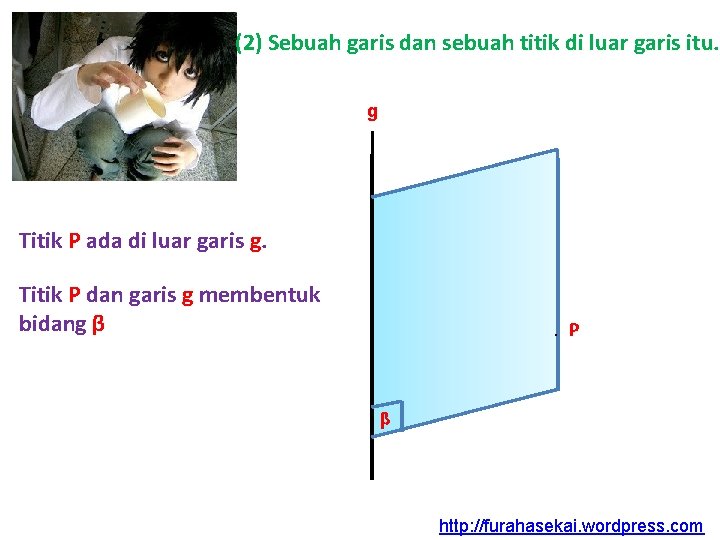
(2) Sebuah garis dan sebuah titik di luar garis itu. g Titik P ada di luar garis g. Titik P dan garis g membentuk bidang β . P β http: //furahasekai. wordpress. com

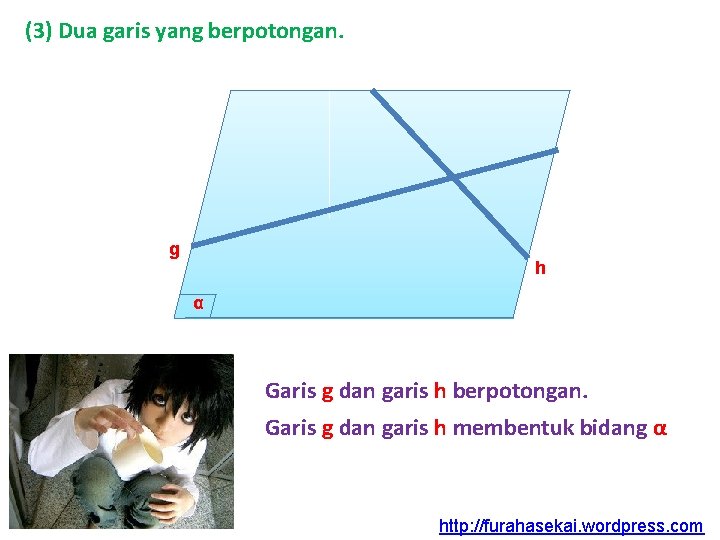
(3) Dua garis yang berpotongan. g h α Garis g dan garis h berpotongan. Garis g dan garis h membentuk bidang α http: //furahasekai. wordpress. com

(4) Dua garis yang sejajar. m β Garis m dan garis n sejajar. Garis m dan garis n membentuk bidang β http: //furahasekai. wordpress. com n

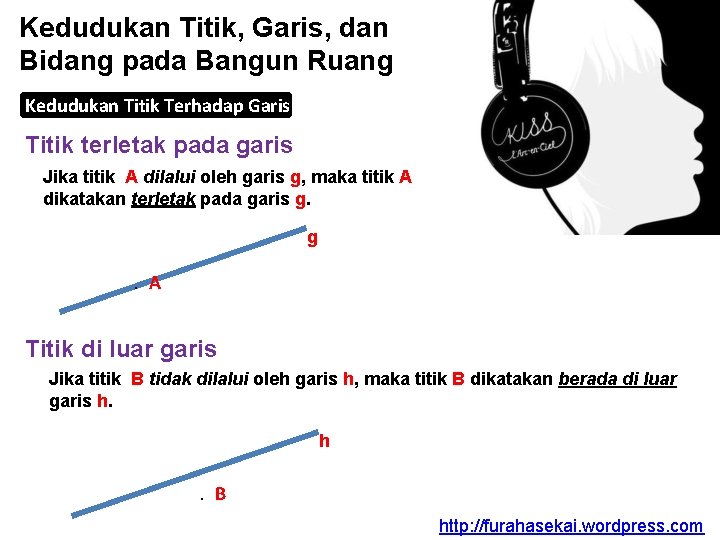
Kedudukan Titik, Garis, dan Bidang pada Bangun Ruang Kedudukan Titik Terhadap Garis Titik terletak pada garis Jika titik A dilalui oleh garis g, maka titik A dikatakan terletak pada garis g. g . A Titik di luar garis Jika titik B tidak dilalui oleh garis h, maka titik B dikatakan berada di luar garis h. h . B http: //furahasekai. wordpress. com

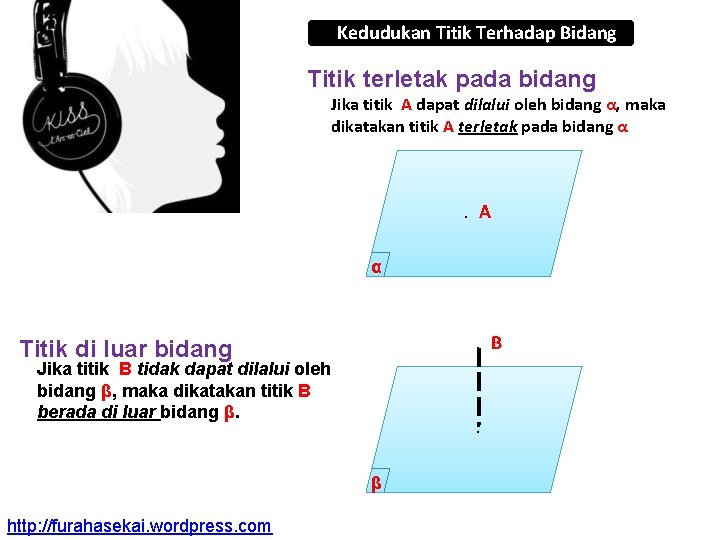
Kedudukan Titik Terhadap Bidang Titik terletak pada bidang Jika titik A dapat dilalui oleh bidang α, maka dikatakan titik A terletak pada bidang α . A α . B Titik di luar bidang Jika titik B tidak dapat dilalui oleh bidang β, maka dikatakan titik B berada di luar bidang β. . β http: //furahasekai. wordpress. com

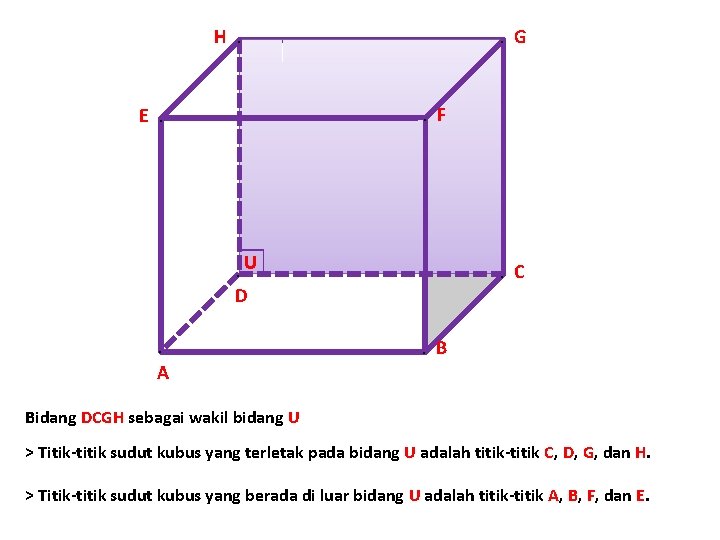
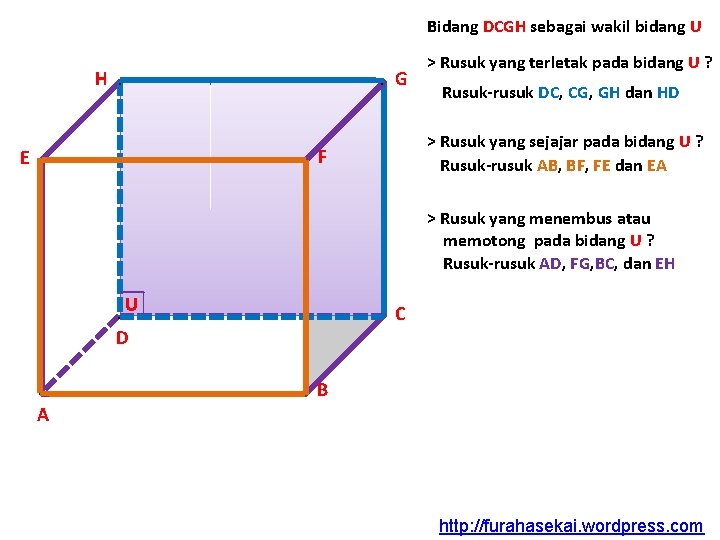
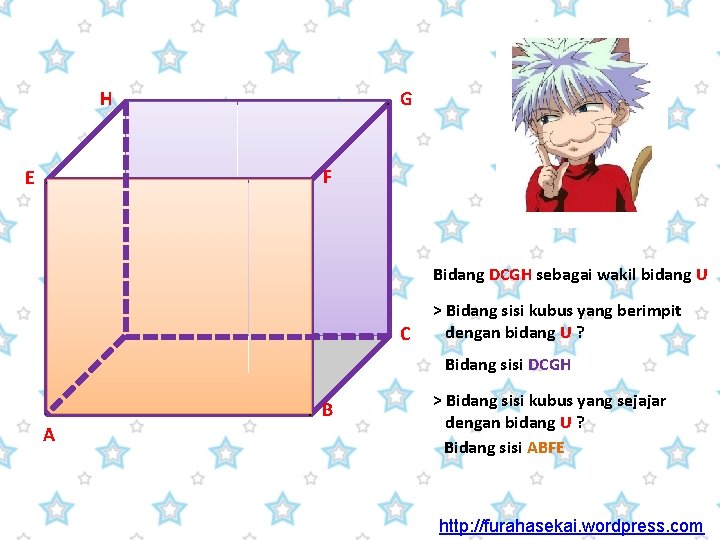
H E . . G. F . . U . C D . A . B Bidang DCGH sebagai wakil bidang U > Titik-titik sudut kubus yang terletak pada bidang U adalah titik-titik C, D, G, dan H. > Titik-titik sudut kubus yang berada di luar bidang U adalah titik-titik A, B, F, dan E.

Kedudukan Dua Garis 1) Berimpit Garis g berimpit dengan garis h jika setiap titik di garis g juga terletak di garis h, dan sebaliknya. g h Syarat untuk dua garis berimpit, cukup memiliki dua titik persekutuan. 2) Berpotongan Garis g dan h berpotongan jika kedua garis tersebut memiliki tepat satu titik persekutuan, yaitu titik potong kedua garis. Dua garis hanya dapat berpotongan jika terletak pada bidang yang sama. h . A g

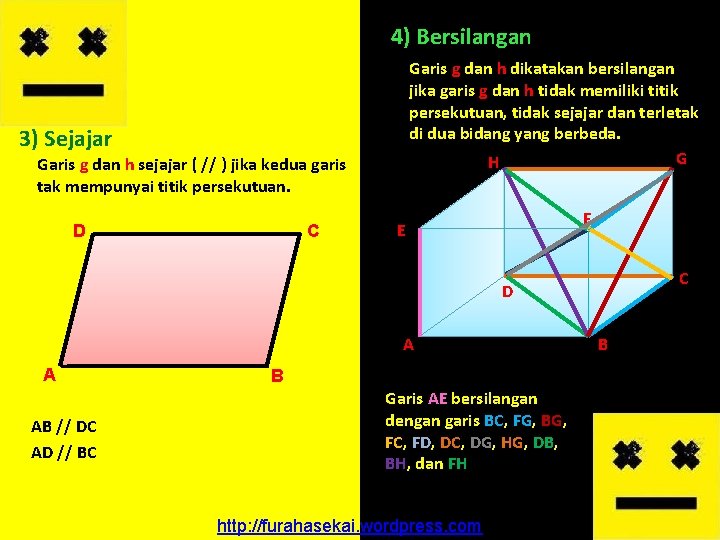
4) Bersilangan Garis g dan h dikatakan bersilangan jika garis g dan h tidak memiliki titik persekutuan, tidak sejajar dan terletak di dua bidang yang berbeda. G H 3) Sejajar Garis g dan h sejajar ( // ) jika kedua garis tak mempunyai titik persekutuan. D C F E C D A A AB // DC AD // BC B Garis AE bersilangan dengan garis BC, FG, BG, FC, FD, DC, DG, HG, DB, BH, dan FH http: //furahasekai. wordpress. com B

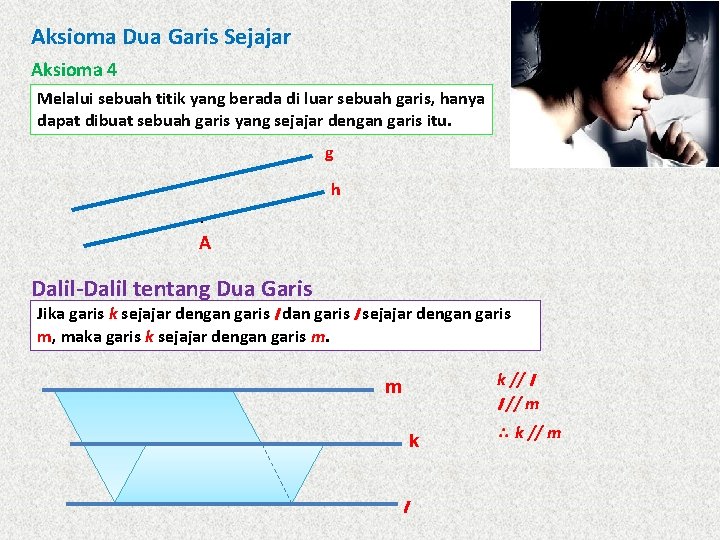
Aksioma Dua Garis Sejajar Aksioma 4 Melalui sebuah titik yang berada di luar sebuah garis, hanya dapat dibuat sebuah garis yang sejajar dengan garis itu. g . h A Dalil-Dalil tentang Dua Garis Jika garis k sejajar dengan garis l dan garis l sejajar dengan garis Sejajar m, maka garis k sejajar dengan garis m. k // l l // m m k l k // m

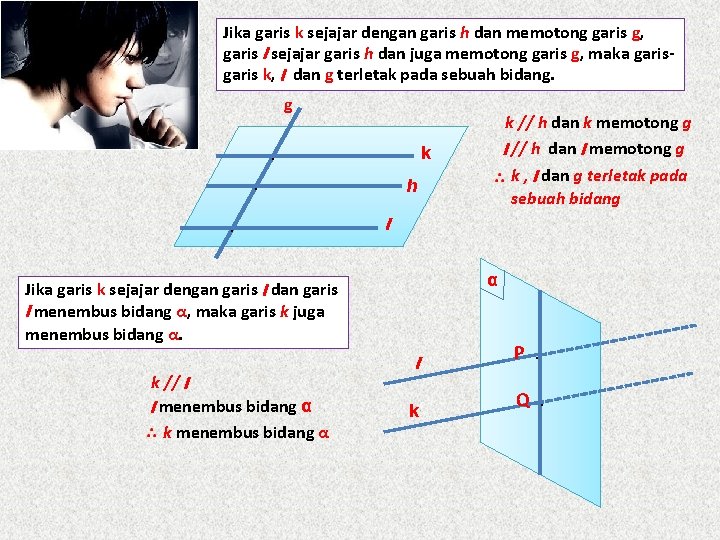
Jika garis k sejajar dengan garis h dan memotong garis g, garis l sejajar garis h dan juga memotong garis g, maka garis k, l dan g terletak pada sebuah bidang. g . . . k h l α Jika garis k sejajar dengan garis l dan garis l menembus bidang α, maka garis k juga menembus bidang α. k // l l menembus bidang α k // h dan k memotong g l // h dan l memotong g k , l dan g terletak pada sebuah bidang l k P . Q .

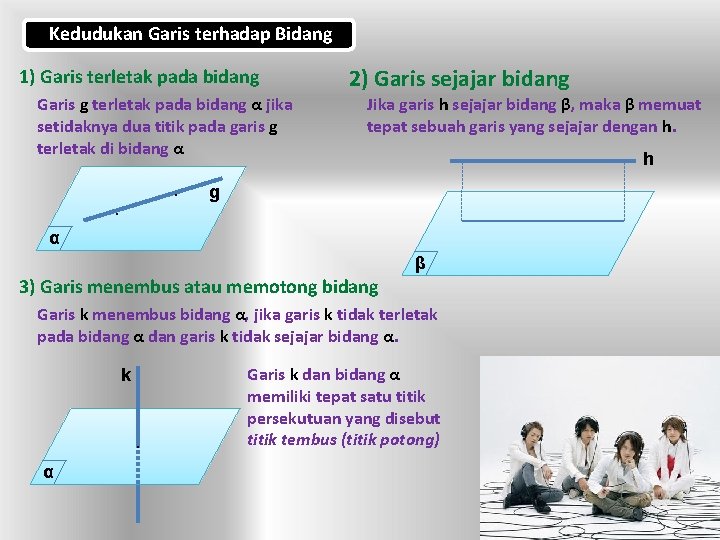
Kedudukan Garis terhadap Bidang 1) Garis terletak pada bidang Garis g terletak pada bidang α jika setidaknya dua titik pada garis g terletak di bidang α . . 2) Garis sejajar bidang Jika garis h sejajar bidang β, maka β memuat tepat sebuah garis yang sejajar dengan h. h g α β 3) Garis menembus atau memotong bidang Garis k menembus bidang α, jika garis k tidak terletak pada bidang α dan garis k tidak sejajar bidang α. k . α Garis k dan bidang α memiliki tepat satu titik persekutuan yang disebut titik tembus (titik potong)

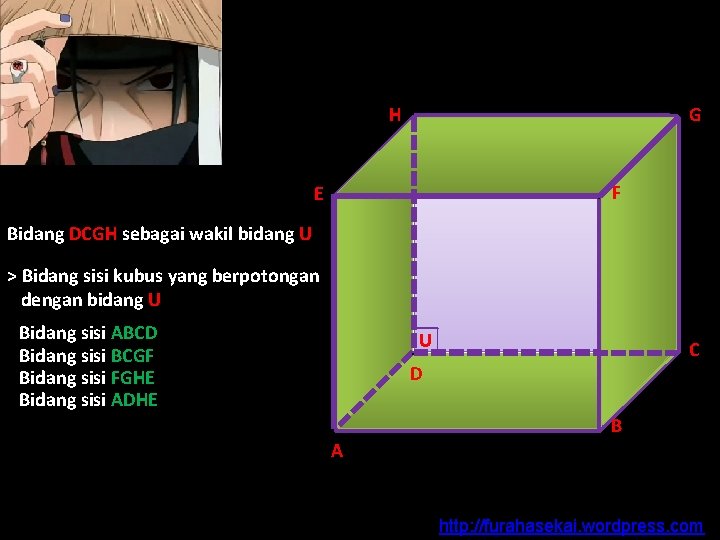
Bidang DCGH sebagai wakil bidang U H E . . G Rusuk-rusuk DC, CG, GH dan HD > Rusuk yang sejajar pada bidang U ? Rusuk-rusuk AB, BF, FE dan EA . F . > Rusuk yang terletak pada bidang U ? > Rusuk yang menembus atau memotong pada bidang U ? Rusuk-rusuk AD, FG, BC, dan EH . U . C D . A . B http: //furahasekai. wordpress. com

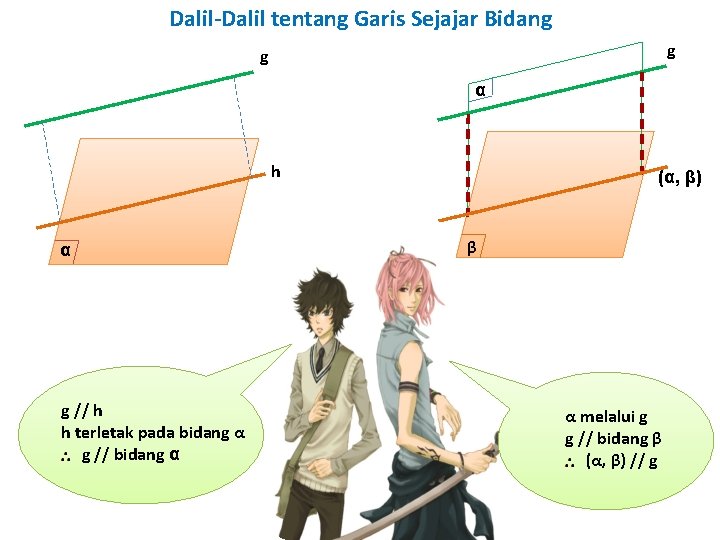
Dalil-Dalil tentang Garis Sejajar Bidang g g α h α g // h h terletak pada bidang α g // bidang α (α, β) β α melalui g g // bidang β (α, β) // g

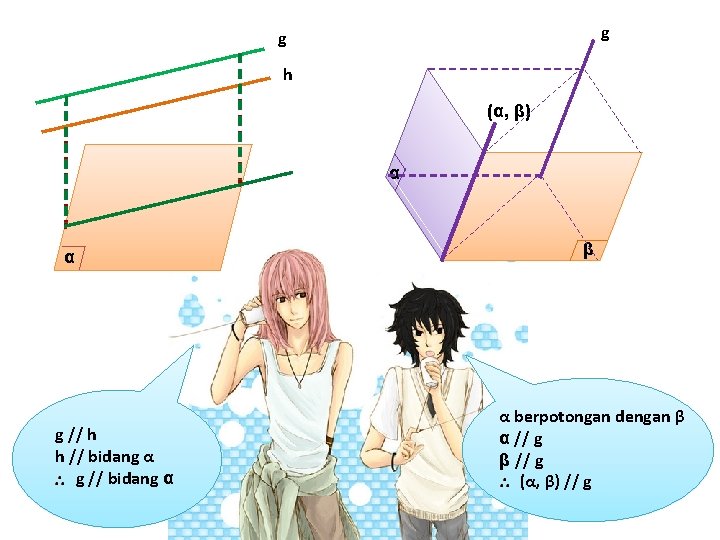
g g h (α, β) α α g // h h // bidang α g // bidang α β α berpotongan dengan β α // g β // g (α, β) // g

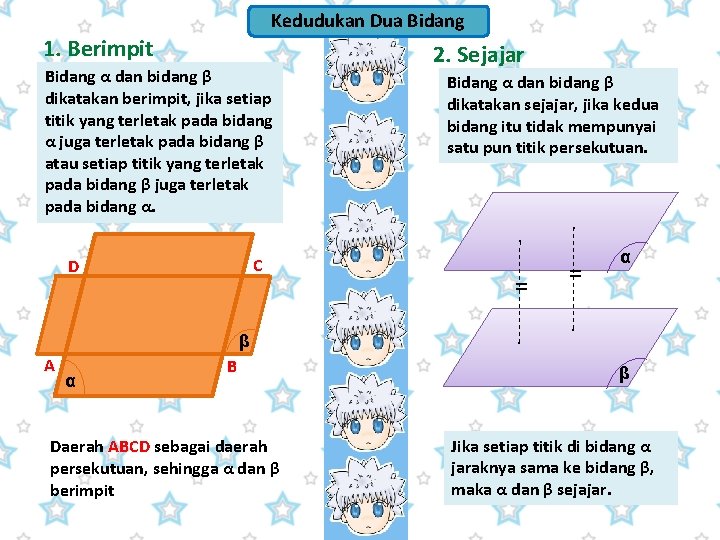
Kedudukan Dua Bidang 1. Berimpit Bidang α dan bidang β dikatakan berimpit, jika setiap titik yang terletak pada bidang α juga terletak pada bidang β atau setiap titik yang terletak pada bidang β juga terletak pada bidang α. C D β A α B Daerah ABCD sebagai daerah persekutuan, sehingga α dan β berimpit 2. Sejajar Bidang α dan bidang β dikatakan sejajar, jika kedua bidang itu tidak mempunyai satu pun titik persekutuan. . = α . β Jika setiap titik di bidang α jaraknya sama ke bidang β, maka α dan β sejajar.

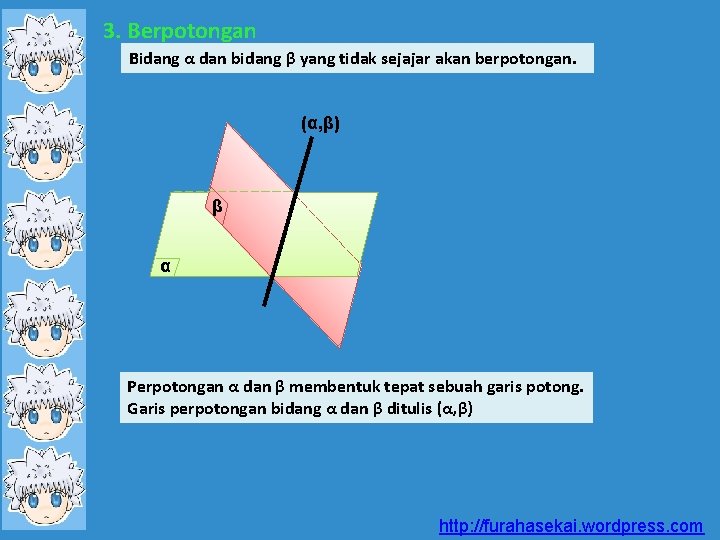
3. Berpotongan Bidang α dan bidang β yang tidak sejajar akan berpotongan. (α, β) β α Perpotongan α dan β membentuk tepat sebuah garis potong. Garis perpotongan bidang α dan β ditulis (α, β) http: //furahasekai. wordpress. com

H E . . G. F . Bidang DCGH sebagai wakil bidang U . C D . A > Bidang sisi kubus yang berimpit dengan bidang U ? Bidang sisi DCGH . B > Bidang sisi kubus yang sejajar dengan bidang U ? Bidang sisi ABFE http: //furahasekai. wordpress. com

H E . . G. F . Bidang DCGH sebagai wakil bidang U > Bidang sisi kubus yang berpotongan dengan bidang U ? Bidang sisi ABCD Bidang sisi BCGF Bidang sisi FGHE Bidang sisi ADHE . U . C D . A . B http: //furahasekai. wordpress. com

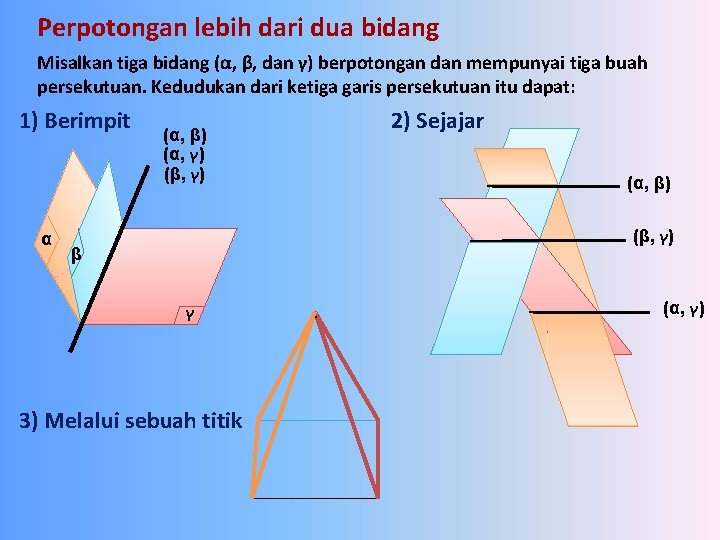
Perpotongan lebih dari dua bidang Misalkan tiga bidang (α, β, dan γ) berpotongan dan mempunyai tiga buah persekutuan. Kedudukan dari ketiga garis persekutuan itu dapat: 1) Berimpit α 2) Sejajar (α, β) (α, γ) (β, γ) (α, β) (β, γ) β γ 3) Melalui sebuah titik . (α, γ)

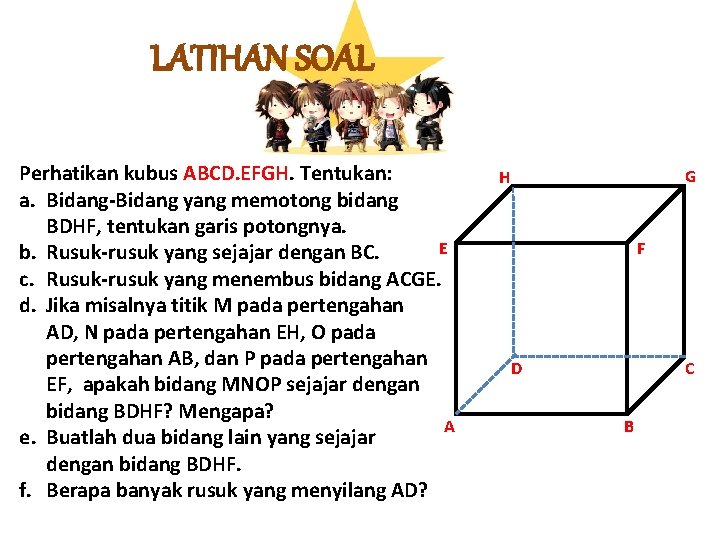
LATIHAN SOAL Perhatikan kubus ABCD. EFGH. Tentukan: a. Bidang-Bidang yang memotong bidang BDHF, tentukan garis potongnya. E b. Rusuk-rusuk yang sejajar dengan BC. c. Rusuk-rusuk yang menembus bidang ACGE. d. Jika misalnya titik M pada pertengahan AD, N pada pertengahan EH, O pada pertengahan AB, dan P pada pertengahan EF, apakah bidang MNOP sejajar dengan bidang BDHF? Mengapa? A e. Buatlah dua bidang lain yang sejajar dengan bidang BDHF. f. Berapa banyak rusuk yang menyilang AD? G H F D C B

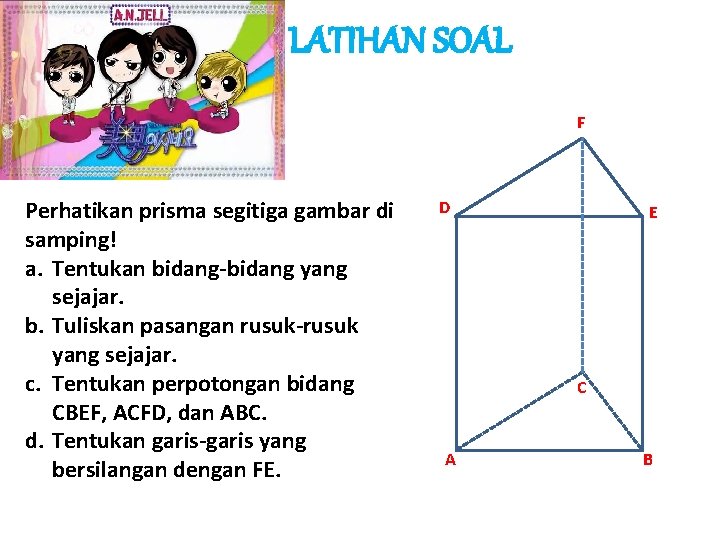
LATIHAN SOAL F Perhatikan prisma segitiga gambar di samping! a. Tentukan bidang-bidang yang sejajar. b. Tuliskan pasangan rusuk-rusuk yang sejajar. c. Tentukan perpotongan bidang CBEF, ACFD, dan ABC. d. Tentukan garis-garis yang bersilangan dengan FE. D E C A B

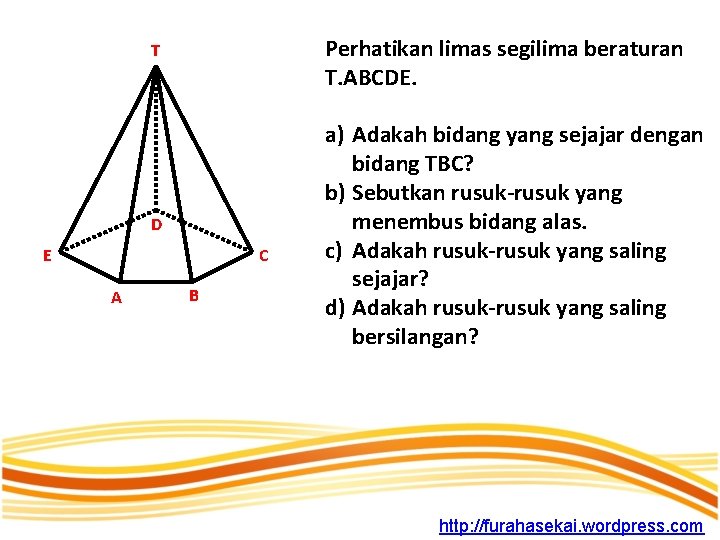
Perhatikan limas segilima beraturan T. ABCDE. T D E C A B a) Adakah bidang yang sejajar dengan bidang TBC? b) Sebutkan rusuk-rusuk yang menembus bidang alas. c) Adakah rusuk-rusuk yang saling sejajar? d) Adakah rusuk-rusuk yang saling bersilangan? http: //furahasekai. wordpress. com

SELAMAT BELAJAR http: //furahasekai. wordpress. com