RTT Most principles of fluid mechanics are adopted

(RTT) • Most principles of fluid mechanics are adopted from solid mechanics, where the physical laws dealing with the time rates of change of extensive properties are expressed for systems. • In fluid mechanics, it is usually more convenient to work with control volumes, and thus there is a need to relate the changes in a control volume to the changes in a system. • The relationship between the time rates of change of an extensive property for a system and for a control volume is expressed by the Reynolds transport theorem (RTT), which provides the link between the system and control volume • RTT is named after the English engineer, Osborne Reynolds (1842– 1912), who did much to advance its application in fluid mechanics.

• The laws in their basic forms are stated in terms of system a system (or Object): a collection of matter of fixed identity (always coame atoms or molecules and always containing same mass no matter moves and interacts with its surrounding). • System approach is NOT very suitable for the applications in fluid mesh is hard to identify and track a group of fluid since moves quite instead, control volume (CV) approach is more often used in fluid mesh.

How to choose a control volume? • CV is arbitrarily chosen by fluid dynamicist, however, selection of CV can either simplify or complicate analysis; • Clearly define all boundaries. Analysis is often simplified if CS is normal to flow direction; • Only CS conditions needed! Do not require detailed information inside CV. • Clearly identify all fluxes crossing the CS; • Clearly identify forces & torques of interest acting on the CV and CS.

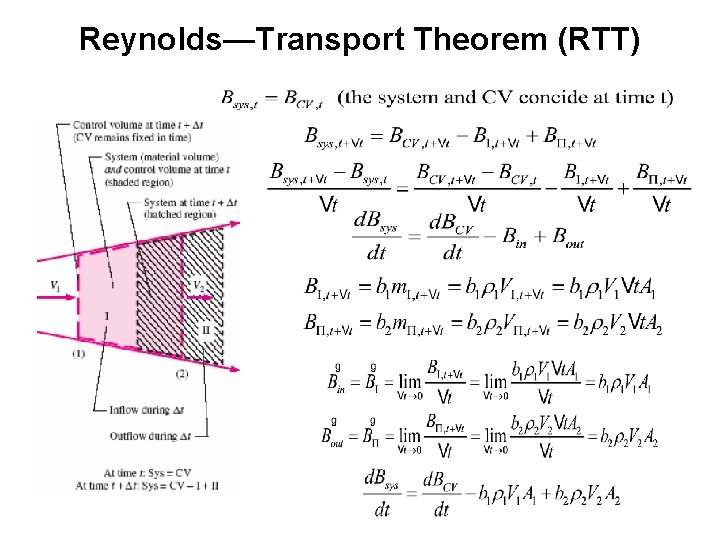
Reynolds—Transport Theorem (RTT)

Reynolds—Transport Theorem (RTT) • the time rate of change of the property B of the system is equal to the time rate of change of B of the control volume plus the net flux of B out of the control volume by mass crossing the control surface.

Reynolds—Transport Theorem (RTT) The total amount of property B within the control volume must be determined by integration: Therefore, the system-to-control- volume transformation for a fixed control volume:

Material derivative (differential analysis): General RTT, non-fixed CV (integral analysis):

Reynolds—Transport Theorem (RTT) • Interpretation of the RTT: – Time rate of change of the property B of the system is equal to (Term 1) + (Term 2) – Term 1: the time rate of change of B of the control volume – Term 2: the net flux of B out of the control volume by mass crossing the control surface

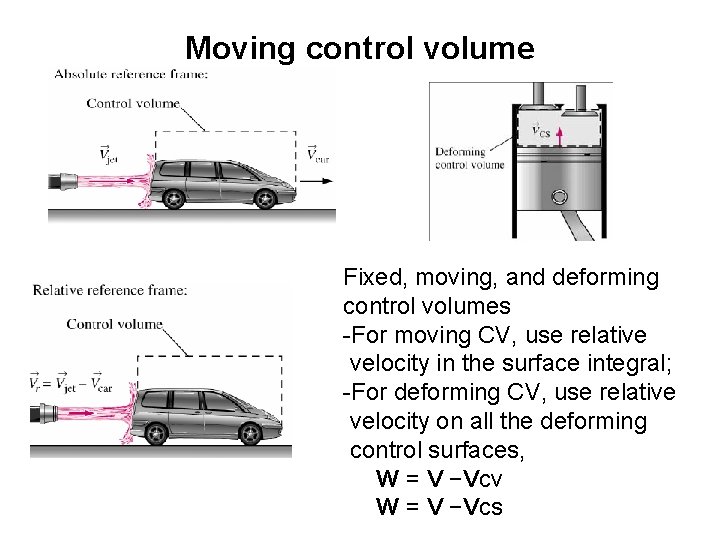
Moving control volume Fixed, moving, and deforming control volumes -For moving CV, use relative velocity in the surface integral; -For deforming CV, use relative velocity on all the deforming control surfaces, W = V −Vcv W = V −Vcs

For moving and/or deforming control volumes, • Where the absolute velocity V in the second term is replaced by the relative velocity Vr = V –VCS • Vr is the fluid velocity expressed relative to a coordinate system moving with the control volume.