Rtree an efficient spatial access method for highly

R++-tree: an efficient spatial access method for highly redundant point data Kalmár Dániel (előadás), Németh Boldizsár (feldolgozás), Hollenczer Péter (implementáció)

A dolgozatról • • • Szerzők: Martin Šumák, Peter Gurský kassai P. J. Šafárik Egyetem ADBIS 2013 konferencián mutatták be

“spatial access method” • • általános probléma: pontok vagy geometriai alakzatok elhelyezése N-dimenziós térben, ezeken keresési műveletek végrehajtása alkalmazás sokrétű: adatbázisok, térinformatika, 3 D modellezés és renderelés, fizikai szimulációk, stb…

Gyakori térbeli keresési problémák • • • range search: adott geometriai forma által befoglalt pontok keresése k. NN (k nearest neighbor): adott pont k db. legközelebbi szomszédjának keresése top-k search: fuzzy értékek között, súlyozással számított összegekben legjobb találatok keresése Ezek a keresések idő hiányában nem lesznek részletesebben bemutatva minden adatstruktúrán hasonlóan működnek és meglepően egyszerűek. A kihívás az adatstruktúra megfelelő felépítése, hogy a keresés minél hatékonyabban fusson.

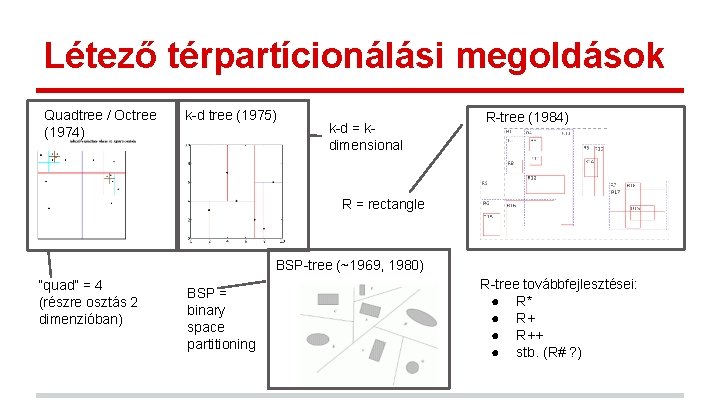
Létező térpartícionálási megoldások Quadtree / Octree (1974) k-d tree (1975) k-d = kdimensional R-tree (1984) R = rectangle BSP-tree (~1969, 1980) “quad” = 4 (részre osztás 2 dimenzióban) BSP = binary space partitioning R-tree továbbfejlesztései: ● R* ● R++ ● stb. (R# ? )

“point data” • • • minden pontokat tartalmazó térpartícionáló megoldás kiterjeszthető geometriai alakzatokra - de nem feltétlen hatékonyan az R++ fa nem nagyon alkalmas erre, így csak pontokkal érdemes foglalkozni hivatalos magyarázat: a kutatás célja (aminek keretében feltalálták) pontszerű adatok feldolgozása volt

“highly redundant” • • • a redundancia itt a pontok közelségére, tömörülésére utal minél nagyobb dimenzióban dolgozunk, annál ritkábbak lesznek a pontok (Curse of Dimensionality) az R++ fa tapasztalat alapján általános esetben csak alacsony dimenziókban működik hatékonyan, de bizonyos esetekben ez nem feltétlen igaz (mérések jönnek)

“efficient”? Hatékonyabb a “legjobb” R* fánál… bizonyos esetekben. Pár mérési eredmény a szerzőktől, generált adatokra:

Pszeudo-valós adatok A szerzők kutatása alapjául szolgáló konkrét probléma adatain vett mérések (6 dimenzióban, de kevesebb attribútumra keresve):

Mérési eredmények értelmezése • • • a dimenziók számával egyenesen arányosan romlik a hatékonysága az R*-hoz képest alacsony dimenziókban általában fel tudja venni a versenyt az R*-gal, de nem feltétlen jobb bárhol viszont bizonyos speciális esetekben jóval gyorsabb (valós adatok, top-k search) megjegyzés: beszúrási hatékonysága sokkal jobb az R*-nál R+-fa: “nehezen” implementálható és lassú

De mi az az R++ fa? • • • az R* és R+ fák továbbfejlesztése (amik az R-fa továbbfejlesztései) megértéséhez ezek megértése szükséges az R-fák általános tulajdonságai: o a szülő a gyerekeit magába ölelő AABB -t (axis aligned bounding box) tárol o csak a levelek tárolnak pontokat o egy node több gyereket is magába foglalhat (nem bináris) o kiegyensúlyozott

Az R-család fái közti különbségek • • a bounding box konkrét tulajdonságai (minimális? átfedés van? ) beszúrásnál a pont helyét megtaláló heurisztika (átfedésnél vagy üres területen) telített node-ok szétvágásának módszere implementációs kérdések

A minimális bounding box probléma Feladat: szúrjuk be a megjelölt pontot egy levélbe (minimális bounding box) Probléma: bármelyik levélbe szúrjuk be, annak a bounding box-át bővíteni kell, és átfedés keletkezik

A maximális bounding box probléma Feladat: szúrjuk be a megjelölt pontot egy levélbe (maximális bounding box) Probléma: mivel a téglalapok maximálisak, a keresés kevésbé lesz hatékony ezen a fán

Eddigi megvalósítások • • R: minimális bounding box, lehet átfedés, beszúrás: ahol a legkevésbé kell növelni a boxot R*: bounding boxban lehet átfedés, beszúrás levél szinten: ahol a legkisebb az átfedés, magasabb szinten: mint R-fa R+: átfedés elkerülése, de egy objektum több levélbe is be lehet szúrva, lassabb felépítés, implementációs problémák split algoritmusok: sokféle, különböző szempontok alapján: átfedés csökkentése, sebesség, keresést lassító helyzetek elkerülése

Az R++ fa titka Hogyan oldjuk meg a min és max bounding box problémákat? Mindkettőt nyilvántartjuk. A maximálisat (br) beszúrásnál használjuk, a minimálisat (mbr) keresésnél. Átfedést nem engedünk meg.

Beszúrási heurisztika • • beszúrásnál br alapján bejárjuk a fát, mbr-t bővítve (ha szükséges) a heurisztika triviális, mivel br maximális (lefedik az egész teret) és átfedésmentes, így minden (a térbe eső) pontra egyértelműen meg tudjuk határozni a haladás irányát

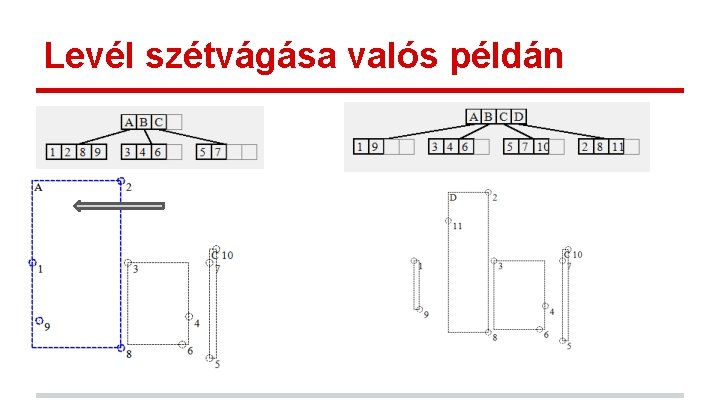
Szétvágó algoritmus (levélre) • minden dimenzióra o • minden pontra a levélben § szétvágjuk a levelet a pont mentén § kiszámoljuk a különbséget a szétvágás két oldalán a minimális különbséget adó szétvágás lesz a levélen a vágás

Levél szétvágása valós példán

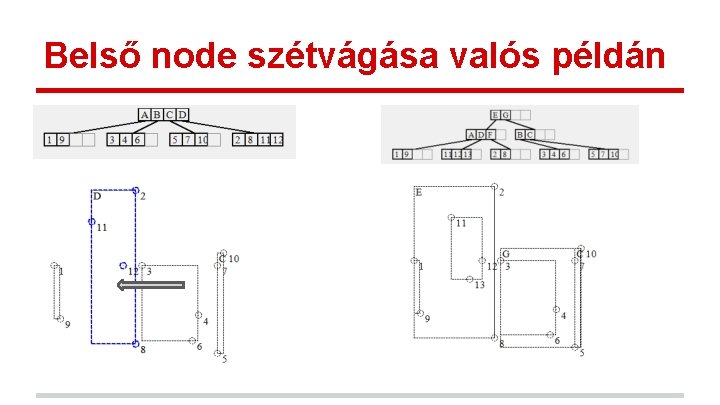
Szétvágó algoritmus (belső node-ra) (belső node = nem levél node) • minden dimenzióra o minden gyerek node-ra § az mbr felső és alsó határára az adott dimenzióban vágjuk szét e mentén, az aktuális dimenzió tengelyére merőlegesen a node-ot o m 1 : = az ezzel szétvágott bounding boxok száma o m 2 : = a nem szétvágott bounding boxok számának különbsége a vágás két oldalán • • a végleges vágás az m 1 -ek minimumát adó vágás lesz o ha több ilyen van, az m 2 alapján döntünk (minimalizálva a különbséget)

Belső node szétvágása valós példán

Vége… Köszönöm a figyelmet! Kérdések?